机载光电平台隔振系统振动耦合分析
2015-12-29杜言鲁,丁亚林,许永森等
机载光电平台隔振系统振动耦合分析
杜言鲁1,2丁亚林1许永森1聂品1
1.中国科学院长春光学精密机械与物理研究所中科院航空光学成像与测量重点实验室,长春,130033
2.中国科学院大学,北京,100049
摘要:为避免载机线振动耦合为光电平台角振动,减小角振动对成像质量和指向精度的影响,对机载光电平台隔振系统进行了分析与研究。针对以往单自由度振动模型仅能分析线振动衰减,无法分析线振动与角振动耦合的缺点,建立了隔振系统的双自由度振动模型,推导出载机线振动与光电平台角振动间的传递函数,分析了减振器刚度、阻尼参数偏差以及减振器布局不合理对振动耦合的影响,为隔振系统的设计和安装提供理论基础。结合工程实际,提出了减小光电平台隔振系统振动耦合的具体措施。
关键词:隔振系统;振动耦合;双自由度模型;传递函数
中图分类号:O328
收稿日期:2014-12-17
基金项目:吉林省科技发展计划资助项目(20140520114JH)
作者简介:杜言鲁,男,1988年生。中国科学院大学博士研究生,就读于中国科学院长春光学精密机械与物理研究所中科院航空光学成像与测量重点实验室。主要研究方向为航空光电载荷稳定成像技术。丁亚林,男,1964年生。中国科学院长春光学精密机械与物理研究所中科院航空光学成像与测量重点实验室研究员、博士研究生导师。许永森,男,1981年生。中国科学院长春光学精密机械与物理研究所中科院航空光学成像与测量重点实验室副研究员。聂品,男,1981年生。中国科学院长春光学精密机械与物理研究所中科院航空光学成像与测量重点实验室助理研究员。
Analysis of Coupled Vibration in Isolation System for Airborne Optoelectronic Pod
Du Yanlu1,2Ding Yalin1Xu Yongsen1Nie Pin1
1.Key Laboratory of Airborne Optical Imaging and Measurement, Changchun Institute of Optics,
Fine Mechanics and Physics,Chinese Academy of Sciences,Changchun,130033
2.University of Chinese Academy of Sciences,Beijing,100049
Abstract:In order to prevent translational aircraft vibratory disturbances from transforming into angular vibration of optoelectronic pod and reduce the influences of angular vibration on the image quality and accuracy of line-of-sight(LOS), a passive isolation system was analyzed and developed. For the point that angular vibration transmissibility could not be analyzed with the model of single degree of freedom, a mathematical model of two degree of freedom vibration isolation system was established. The transfer function between translational aircraft vibration and rotational responses of optoelectronic pod was derived. The coupled vibration in isolation system with stiffness error , damping error and unreasonable layout were analyzed.These analyses provided theoretic basis for the design and assembly of the vibration isolation system. Finally, combining engineering practices, the methods to reduce angular vibration from aircraft linear vibration were proposed.
Key words:vibration isolation system; coupled vibration; model of two degree of freedom; transfer function
0引言
机载光电平台作为目前获取地面目标图像的主要光电设备之一,具有机动灵活、实时准确、范围广、针对性强等特点,已广泛应用于地形测绘、军事侦察等领域[1]。随着光电平台光学系统成像分辨率的提高,振动成为限制其成像质量和指向精度的重要因素之一,而且角振动的影响远远大于线振动的影响[2-4],因此在隔振系统设计中应避免线振动耦合为角振动。被动隔振以其结构简单、经济实用、无需能源等优点,成为光电平台振动抑制的主要方法之一[5]。但被动隔振系统往往因减振器设计或安装不合理,导致载机线振动耦合为光电平台角振动,使得成像质量下降,指向精度降低,因此研究隔振系统中振动耦合问题,对机载光电平台减振装置设计具有重要的指导意义。
国内外许多学者对机载光电平台隔振系统进行了分析和设计。赵鹏等[6]指出隔振系统中各减振器刚度、平台重心与减振器的支撑中心不重合等使得各安装点处的振幅或相位不同,引起平台角振动。董斌等[7]通过对隔振系统进行分析,给出了在忽略阻尼情况下避免产生角振动的隔振系统中减振器刚度、安装间距应满足的量化关系。文献[8-10]根据平行四边形原理或空间连杆机构,设计无角位移隔振装置,避免载机线振动与平台角振动耦合,但仅适用于尺寸较小的光电设备。以上针对隔振系统建立的模型大多为单自由度振动模型,无法用于分析线振动与角振动耦合问题。本文通过建立隔振系统的双自由度振动模型,依据线性系统的传递函数理论,定量地分析了隔振系统中各参数偏差对振动耦合的影响,并结合工程实际,提出减小光电平台角振动的具体措施。
1隔振系统双自由度振动模型
目前,对于尺寸较大的光电平台,依然采用四个固定点的隔振方式,即将光电平台通过4个减振器与载机相连。然而在实际工程中,各减振器间参数不一致或减振器布局不合理,使得载机线振动耦合为光电平台角振动。为定量分析隔振系统参数偏差对振动耦合的影响程度,在X、Y、Z 3个轴向上分别建立隔振系统的双自由度振动模型[11],如图1所示。其中O点为光电平台质心,m、I0为平台质量和绕过质心且垂直纸面轴的转动惯量,k1、k2为连接点处减振器刚度,c1、c2为减振器阻尼系数,l1、l2为安装点与相机质心间的间距,L为平台质心与安装平面间的间距,xi为载机线振动,y为经Y方向隔振后光电平台的线振动,x、θ分别为平台X方向上的线振动和平台绕质心的角振动。
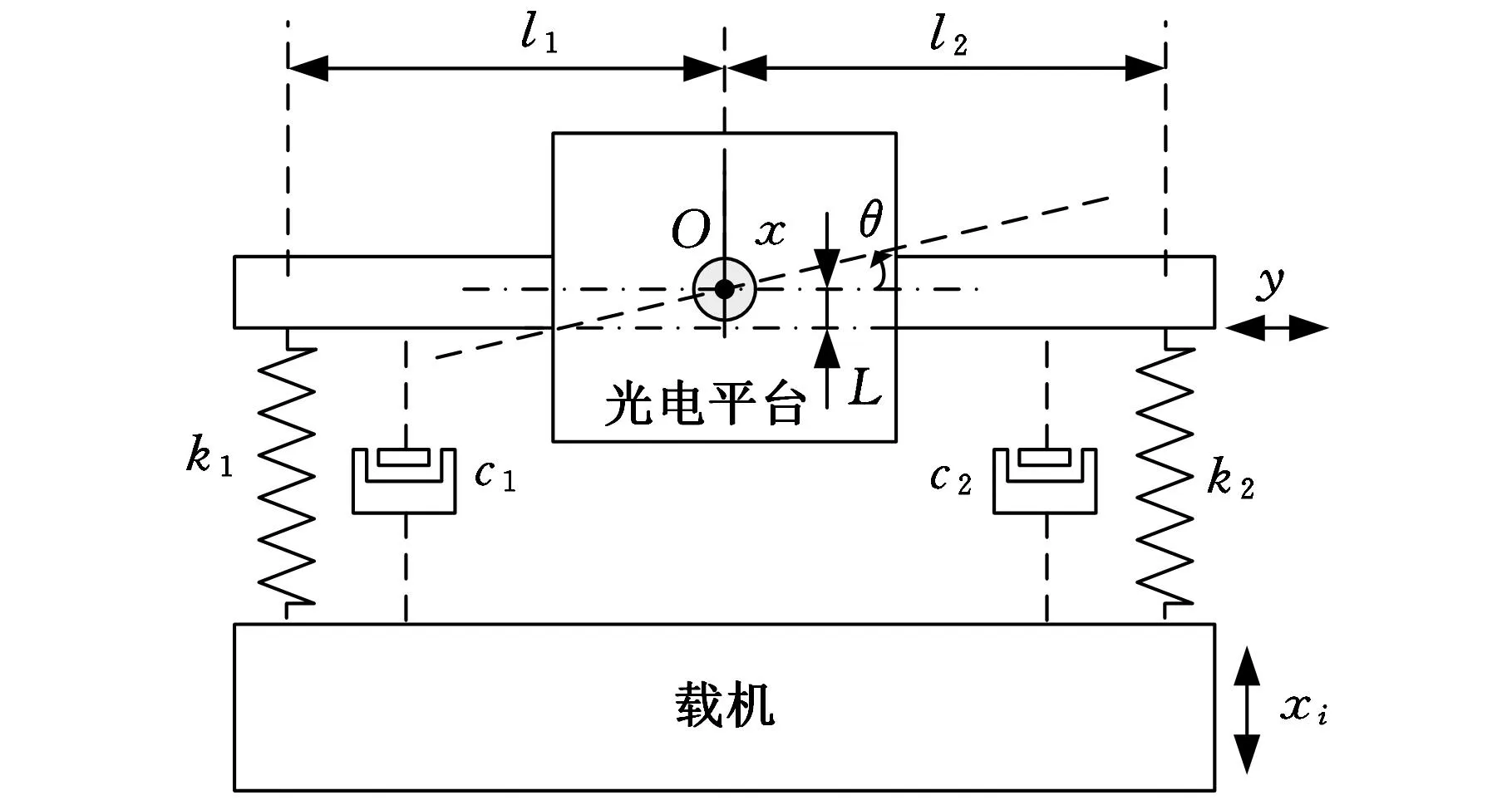
图1 隔振系统双自由度振动模型
建立机载光电平台隔振系统的运动微分方程如下:
(1)
假设隔振系统初始条件均为0,即

对运动微分方程进行拉普拉斯变换后整理得
(2)
由于本文主要分析隔振系统中振动耦合问题,因此引入载机线振动到光电平台角振动的传递函数(或称为传递率,即光电平台角振动幅值与载机线振动幅值之比),描述载机线振动经隔振系统后耦合为光电平台角振动的幅值情况,用于分析隔振系统的振动耦合情况,传递率越大,振动耦合越严重。对式(2)进行代数运算后可得,在不考虑Y方向线振动时,载机X方向线振动到光电平台角振动的传递函数为
(3)
而在不考虑X方向线振动时,Y方向线振动到光电平台角振动的传递函数为
(4)
Ax(s)=m(-c1l1+c2l2)s3+m(-k1l1+k2l2)s2
Ay(s)=[ms2+(c1+c2)s+(k1+k2)]s2L
(k1c2+k2c1)(l1+l2)2s+k1k2(l1+l2)2
由式(3)和式(4)可知,当隔振系统中刚度、阻尼以及安装间距满足以下关系
k1l1=k2l2且c1l1=c2l2且L=0
时,则有θ(s)≡0,即载机线振动只会引起光电平台沿X、Y方向上的线振动而不会耦合为光电平台角振动。此时光电平台隔振系统线振动、角振动的有阻尼固有频率分别为
(5)
在机载光电平台隔振系统设计中,式(5)在减振器选择和布局上具有重要的指导意义。通常根据光电平台稳像系统的伺服带宽确定隔振系统的固有频率[12],并将线振动、角振动的有阻尼固有频率设计为相等,线振动固有频率ωn用于确定减振器的刚度,而角振动固有频率ωnr用于确定减振器的安装间距。
2参数偏差对振动耦合影响分析
实际工程中,隔振系统中各减振器参数间不可避免地存在差异,光电平台质心与支撑中心间存在偏差,绝对的对称布置很难保证,此时载机线振动将引起光电平台角振动。根据推导出的载机线振动到光电平台角振动的传递函数,可对各参数偏差对隔振系统振动耦合程度的影响进行分析。为便于分析,定义刚度、阻尼和安装间距的相对偏差量分别为
下面以某型号机载光电平台隔振系统[12]为例进行分析,设计线振动和角振动的有阻尼固有频率均为4Hz,隔振系统具体设计参数如表1所示。

表1 某机载光电平台隔振系统参数
(a)存在刚度偏差时

(b)存在阻尼偏差时

(c)安装偏心时
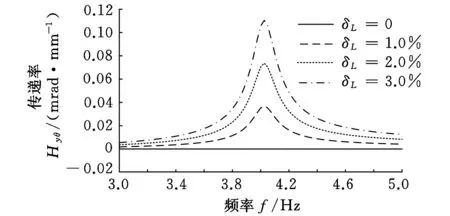
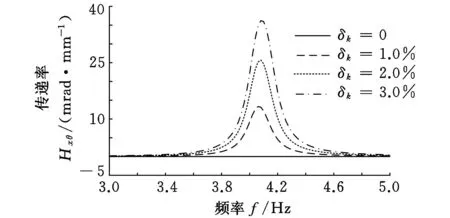
(d)偏离安装平面时 图2 隔振系统参数偏差对振动耦合的影响
由于存在加工、安装误差,使得隔振系统参数相对于设计参数值有一定的偏差,下面对不同参数偏差下载机线振动到光电平台角振动的传递率进行仿真分析,仿真结果如图2所示,图中分别绘制了在仅有刚度、阻尼、安装偏差时的载机线振动到光电平台角振动的传递曲线。可见隔振系统中各参数存在偏差时均会导致载机线振动耦合为光电平台角振动,而且参数偏差越大,振动耦合程度越严重;刚度、阻尼以及安装间距存在偏差时,在谐振频率处载机线振动引起光电平台角振动最为严重,在高频区振动耦合程度较小;当平台质心偏离减振器安装平面时,安装平面内的线振动也会引起平台角振动;但刚度偏差、安装间距偏差对振动耦合的影响相对较大,而阻尼偏差、质心偏离安装平面对振动耦合的影响相对较小。
为进一步分析隔振系统中各参数偏差对振动耦合程度的影响,绘制出在频率4Hz处不同参数偏差下载机线振动到光电平台的传递率曲线,如图3所示。从图中可看出,当参数偏差较小时,载机线振动到平台角振动的传递率基本上与参数偏差成线性关系,而且平台质心与减振器支撑中心的偏差、减振器刚度偏差对振动耦合的影响远远大于阻尼偏差、质心偏离安装平面对振动耦合的影响,因此在隔振系统设计、安装过程中应严格保证各减振器的刚度一致以及平台质心与支撑中心重合,否则会导致光电平台存在幅值较大的角振动,严重影响其成像质量和指向精度。

图3 不同参数偏差在4Hz处线振动到角振动的传递率
3载机线振动与平台角振动耦合分析
随着机载光电平台光学系统成像分辨率的提高,载机振动成为限制光电平台性能的重要因素之一,为此国外飞机制造商对载机实际飞行中的振动情况进行了测试,图4为波音公司给出的某载机的线振动位移功率谱密度曲线。下面以此载机随机振动功率谱密度曲线作为隔振系统输入,根据上述振动耦合模型,分析载机线振动经隔振系统后耦合为光电平台角振动的情况。对于随机振动的传递,设输入的载机随机线振动的功率谱密度为Sx(ω),隔振系统的传递函数为H(jω),则经隔振系统后光电平台的角振动功率谱密度Sθ(ω),可由下式计算[13]:
Sθ(ω)=|H(jω)|2Sx(ω)

图4 载机线振动位移功率谱密度曲线
于是可得出光电平台的角振动位移功率谱密度,图5所示为在安装间距偏差δl为3%时,光电平台的角振动功率谱密度曲线。

图5 光电平台耦合角振动功率谱密度曲线(δ l=3%)
根据光电平台角振动功率谱密度曲线,可计算出经隔振系统耦合的角振动均方根值(RMS)[13],表2~表4分别给出了在仅有刚度偏差、阻尼偏差、安装间距偏差时耦合角振动的均方根值。

表2 存在刚度偏差时耦合角振动RMS值

表3 存在阻尼偏差时耦合角振动RMS值

表4 存在安装偏差时耦合角振动RMS值
可见,当存在参数偏差时,载机线振动经隔振系统后,耦合为光电平台的角振动达到102μrad量级,而通常高分辨光电平台视轴稳定精度要求在微弧度量级[14],因此,此时耦合的角振动将严重影响光电平台的成像质量和指向精度。
4结论
为分析机载光电平台隔振系统振动耦合问题,建立了隔振系统的双自由度振动模型,分析各参数偏差对振动耦合的影响;以载机线振动功率谱密度曲线为输入,计算出光电平台耦合角振动的均方根值,该值远大于光电平台的视轴稳定精度要求,因此要严格控制隔振系统中各参数偏差,避免载机线振动耦合为光电平台角振动。
通过隔振系统双自由度振动模型的分析结果,结合工程实际,总结归纳出隔振系统的设计原则:①根据光电平台稳像系统的伺服带宽确定隔振系统的固有频率,并设定线振动和角振动的固有频率相等,线振动固有频率用于确定减振器刚度,角振动固有频率用于确定减振器间的安装间距,根据视轴稳定系统主动补偿的幅值范围确定隔振系统的阻尼比;②隔振系统安装过程中,要测量平台重心位置,通过合理选择和布局减振器,保证平台质心位于安装平面内,而且阻尼器选择可调式阻尼器,以便调整隔振系统的阻尼系数,使得隔振系统各参数间尽量满足无角振动时的量化关系,减小或避免振动耦合。
参考文献:
[1]贾平,张葆.航空光电侦察平台关键技术及其发展[J].光学精密工程, 2003, 11(1): 82-87.
Jia Ping, Zhang Bao. Critical Technologies and Their Development for Airborne Opto-electronic Reconnaissance Platforms[J]. Optics and Precision Engineering, 2003, 11(1): 82-87.
[2]范国滨,贾建援,陈贵敏,等.机械振动对光学系统指向精度的影响[J].中国机械工程,2005,16(2):104-111.
Fan Guobin, Jia Jianyuan, Chen Guimin, et al. Vibration Effects on Pointing Precision of Optical System[J].China Mechanical Engineering, 2005, 16(2):104-111.
[3]李玉龙,何忠波,白鸿柏,等.角振动对光学成像系统传递函数影响分析[J].中国机械工程,2012,23(15):1784-1788.
Li Yulong, He Zhongbo, Bai Hongbai, et al. Analysis of Influences of Angular Vibration on MTF in Optical Imaging System[J].China Mechanical Engineering, 2012, 23(15):1784-1788.
[4]刘家燕,程志峰,王平.机载光电吊舱橡胶减振器的设计与应用[J].中国机械工程,2014,25(10):1308-1312.
Liu Jiayan, Cheng Zhifeng, Wang Ping. Design and Applications of Rubber Shock Absorber in Airborne Photoelectric Pod[J].China Mechanical Engineering, 2014, 25(10):1308-1312.
[5]姜伟伟,徐治洲,任戈. 机载光电成像设备减振系统仿真及试验[J].噪声与振动控制, 2014, 34(3):186-189.
Jiang Weiwei, Xu Zhizhou, Ren Ge. Simulation and Experiment Validation of the Vibration Absorbing System of an Airborne Photoelectric Imaging Equipment[J]. Noise and Vibration Control, 2014, 34(3):186-189.
[6]赵鹏,杨牧,张葆.航空机载光学设备的振动分析及座架减震器的设计[J].光学 精密工程,1997,5(3):58-63.
Zhao Peng, Yang Mu, Zhang Bao. The Vibration Analysis and Damper Design of Optic Instrument in FlyingPlatform[J]. Optics and Precision Engineering, 1997, 5(3): 58-63.
[7]董斌,丁亚林,田海英,等.新型航空光学遥感器减振结构设计[J].光学精密工程,2008,16(12):2454-2459.
Dong Bin, Ding Yalin, Tian Haiying, et al.Design of Vibration Absorbing Structure for Aerial Remote Sensor[J]. Optics and Precision Engineering, 2008, 16(12): 2454-2459.
[8]李玉龙,何忠波,白鸿柏,等.光电吊舱无角位移被动减振系统研究[J].振动与冲击,2012,31(16):88-91.
Li Yulong, He Zhongbo, Bai Hongbai, et al.Non-angular Displacement Passive Vibration Isolation System for Optical Pod[J]. Journal of Vibration and Shock, 2012,31(16):88-91.
[9]刘树峰,白鸿柏,李冬伟,等.光电平台新型隔振机构设计[J].机械设计,2012,29(2):16-19.
Liu Shufeng, Bai Hongbai, Li Dongwei, et al.Design of a Novel Damping Mechanism for the Opto-electronic Platform[J]. Journal of Machine Design, 2012, 29(2):16-19.
[10]王平,张国玉,刘家燕,等.机载光电吊舱无角位移隔振设计[J].红外与激光工程,2012,41(10):2799-2804.
Wang Ping, Zhang Guoyu, Liu Jiayan, et al.Irrotational Displacement Vibration Isolation on Airborne Optoelectronic Pod[J]. Infrared and Laser Engineering, 2012, 41(10):2799-2804.
[11]丁文镜.减振理论[M].北京:清华大学出版社,1998.
[12]Toole J O. Passive Vibration Isolation for Long Range Aerial Reconnaissance Systems[J]. Proceedings of Society of Photo-Optical Instrumentation Engineers,1980,250:77-86.
[13]纽兰 D E.随机振动与谱分析概论[M].方同,黄嘉璜,朱位秋,等译.北京:机械工业出版社,1980.
[14]Held K J, Robinson B H. TIER Ⅱ Plus Airborne EO Sensor LOS Control and Image Geolocation[J]. IEEE Aerospace Conference Proceedings,1997,2:377-405.
(编辑苏卫国)

