基于ASTFA降噪和AKVPMCD的滚动轴承故障诊断方法
2015-12-29杨宇,李紫珠,何知义等
基于ASTFA降噪和AKVPMCD的滚动轴承故障诊断方法
杨宇李紫珠何知义程军圣
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
摘要:提出了一种滚动轴承故障诊断的新方法。首次将自适应最稀疏时频分析(ASTFA)方法应用于振动信号的降噪,并针对KVPMCD方法只选择一种最佳相关模型而忽略其他几种相关模型对预测精度贡献的缺陷,提出了一种改进的KVPMCD模式识别算法——人工鱼群算法优化融合Kriging模型的基于变量预测模型的模式识别(AKVPMCD)算法,即采用收敛速度快、鲁棒性强、具有全局寻优能力的人工鱼群智能算法(AFSIA)优化融合多种Kriging相关模型来提高模型预测精度。在此基础上,提出了一种基于ASTFA降噪和AKVPMCD算法的滚动轴承故障诊断方法。实验结果表明,该方法可以有效提高分类识别的精度。
关键词:自适应最稀疏时频分析降噪;AKVPMCD;滚动轴承;故障诊断
中图分类号:TH113
收稿日期:2014-11-20
基金项目:国家自然科学基金资助项目(51175158,51375152);湖南省自然科学基金资助项目(11JJ2026)
作者简介:杨宇,女,1971年生。湖南大学机械与运载工程学院教授、博士研究生导师。主要研究方向为动态信号处理、机电设备状态监控与故障诊断、模式识别等。李紫珠,男,1990年生。湖南大学机械与运载工程学院硕士研究生。何知义,男,1990年生。湖南大学机械与运载工程学院硕士研究生。程军圣,男,1968年生。湖南大学机械与运载工程学院教授、博士研究生导师。
The Rolling Bearing Fault Diagnosis Method Based on ASTFA De-noising and AKVPMCD
Yang Yu Li Zizhu He ZhiyiCheng Junsheng
State Key Laboratory of Advanced Design and Manufacture for
Vehicle Body,Hunan University,Changsha,410082
Abstract:A new rolling bearing fault diagnosis method was proposed. ASTFA method was applied to the vibration signal de-noising for the first time.Aiming at the defects of KVPMCD(Kriging model variable predictive model based class discriminate) method that was chosen one of the best related model only and the other correlation models’ contribution to the prediction accuracy was ignored,an improved KVPMCD pattern recognition algorithm AKVPMCD was proposed,the AFSIA(artificial fish swarm intelligence algorithm) which had high convergence speed, strong robustness and global optimization ability was used to optimize a variety of Kriging models,so as to improve the prediction precision. On the basis of above, a new fault diagnosis method of rolling bearings was proposed based on ASTFA de-noising and AKVPMCD. The experimental results prove that this method can improve the precision of classification recognition effectively.
Key words:adaptive and sparsest time-frequency analysis(ASTFA) de-noising;artificial fish swarm algorithm optimizing fusion Kriging model variable predictive model based class discriminate(AKVPMCD);rolling bearing; fault diagnosis
0引言
滚动轴承是各种旋转机械中应用最广泛的一种通用机械部件,滚动轴承故障是旋转机械最主要的故障来源之一。因此,对滚动轴承的工作状态进行实时监测和故障诊断在工程应用中具有十分深远的意义。
滚动轴承故障诊断的本质是模式识别。应用比较广泛的模式识别方法有贝叶斯[1]、粗糙集[2]、神经网络[3]、支持向量机[4]等,但这几种模式识别方法都忽略了所提取特征变量的相互内在关系。Raghuraj等[5]提出了一种新的模式识别方法——基于变量预测模型的模式识别(variable predictive model based class discriminate,VPMCD)方法。该方法认为原始数据中所提取的全部或部分特征值之间存在一定的相互内在关系,通过建立数学模型,使用各种样本数据对模型参数进行估计,从而得到不同类型的预测模型,最终采用预测模型对测试样本进行分类。该方法同样适用于多变量描述的非线性系统的模式识别问题。但由于该方法采用的数学模型为单纯的回归模型,当故障特征之间关系复杂、存在较强的空间相关性时,会使该方法的预测精度受到影响。为了克服这种缺陷,笔者曾将Kriging模型引入VPMCD方法中进行改进从而提出了KVPMCD(Kriging model variable predictive model based class discriminate)方法[6],但是KVPMCD方法中只选择了一种相关模型对回归模型进行补充,而忽略了其他几种相关模型对预测精度的贡献。针对这种缺陷,本文应用具有一定自适应能力、鲁棒性强、收敛速度快,能够全局寻优的人工鱼群智能算法优化融合Kriging估计的几种相关模型,提出了AKVPMCD(artificial fish swarm algorithm optimizing fusion Kriging model variable predictive model based class discriminate)方法。模式识别的另一关键是特征提取。模糊熵是在模糊集和熵的基础上发展而来的一种衡量系统复杂性的度量指标[7],可应用于非线性问题的处理。在滚动轴承不同类型的局部故障下采集的振动信号的复杂程度和不规则程度都有着明显的差异。因此,模糊熵非常适合作为滚动轴承振动信号的特征值来进行故障模式分类。均方根值是表示动态信号强度的指标,峭度则反映了信号概率密度函数峰顶的凸平度,均方根值和峭度对滚动轴承的运行状态、故障和缺陷等足够敏感,适合作为滚动轴承振动信号的特征值来进行运行状态的分类识别。这三个特征值尤其是模糊熵对噪声十分敏感,如果不采取适当的降噪方法对滚动轴承的振动信号进行降噪处理,将会严重影响该分类器的识别精度。
通过数据采集装置所得到的滚动轴承振动信号往往包含各种噪声,在某些情况下噪声干扰甚至大于实际的真实信号。因此,必须有效滤除滚动轴承振动信号中的噪声信号,提高信噪比,提取淹没在噪声中的有用信息,才能获得正确的分析结果。
在传统的信号处理方法中,降噪是通过频谱分析技术来实现的。当噪声与信号在频域可分时,可以设计适当的滤波器将噪声所对应的频带滤除掉[8]。然而,在处理具有显著的非平稳性且频谱成分比较复杂的振动信号时,传统滤波降噪的方法就不能够满足要求。虽然小波降噪[9]相对于传统方法降噪效果有明显的提升,但小波分解的层数在实际应用中需要依靠一定的先验知识和反复的实验来确定。经验模态分解(empirical mode decomposition,EMD)方法[10]也可以对振动信号进行降噪,但该方法存在一定程度的自身缺陷与局限性,如EMD方法在分解信号时分解得到的分量存在一定程度的失真,还存在端点效应与频率混淆以及缺少理论模型和数学基础等问题。
自适应最稀疏时频分析(adaptive and sparsest time-frequency analysis,ASTFA)是Hou等[11-12]受EMD与压缩感知理论启发,于2011年提出的一种基于高斯-牛顿迭代法和快速傅里叶变换(fast Fourier transform,FFT)的自适应最稀疏时频分析方法。该方法采用高斯-牛顿迭代法进行优化,将信号分解问题转化为非线性优化的问题,将信号分解为若干个内禀模态函数(intrinsic mode functions,IMF)之和,其中优化目标为得到非线性信号的最稀疏表示,约束条件为所有IMF都处于过完备字典库{α(t)cos(θ(t)),θ′(t)≥0}中,且α(t)比cos(θ(t))更平滑,从而对原始信号有效地进行分解。因此,本文将ASTFA方法首次应用于振动信号的降噪。
基于上述分析,本文提出了基于ASTFA降噪和AKVPMCD的滚动轴承故障诊断方法,即首先采用ASTFA方法对滚动轴承振动信号进行分解,得到若干个瞬时频率具有物理意义的IMF分量;接着用相关系数法建立噪声评判机制,对信号进行降噪;然后提取对降噪后信号的冲击特征敏感的模糊熵、均方根值、峭度作为特征值,组建特征值矩阵;将特征值矩阵分为训练样本与测试样本分别输入AKVPMCD分类器进行训练和测试,从而对滚动轴承的工作状态和故障类型进行分类识别。为了检验AKVPMCD方法的优越性,将其分类预测结果与原VPMCD方法以及KVPMCD方法的结果进行对比,实验信号的分析结果表明了本文所提方法的有效性和优越性。
1ASTFA降噪理论
ASTFA是一种基于最稀疏分解和过完备字典库的新的时频分析方法。虽然通过观察发现大量多尺度信号在物理域表示很复杂,但通常它们在时频域中都能表示为内禀稀疏结构的形式。由于这种稀疏表示只对某些先验未知、自适应于信号的多尺度基有意义,因此搜寻适当的非线性多尺度基是该方法的一个重要步骤。为了寻找最佳的内禀稀疏结构,将信号分解问题转换为过完备字典库中的非线性优化问题。建立的过完备字典库D如下:
D={α(t)cos(θ(t)):θ′(t)≥0,α(t)∈V(θ)}
(1)
V(θ)=
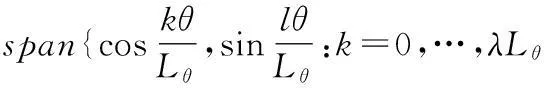
(2)
其中,α为待分解信号的局部均值函数;θ为频率函数,θ′(t)≥0是为了保证瞬时频率具有物理意义;约束α(t)∈V(θ)的目的是令α(t)比cos(θ(t))更平滑;V(θ)为比cos(θ(t))更平滑的α(t)的扩张空间;λ≤1/2为控制V(θ)中函数平滑度的参数;Lθ=(θ(1)-θ(0))/2π。
字典库D某种程度上可以看成IMF分量的集合,由于字典库D高度冗杂且其中的内禀稀疏结构不唯一,为了搜寻到最佳的内禀稀疏结构,将信号分解问题转换为如下非线性优化问题P:
(3)

(1)令r1(t)=f(t);
(2)解决以下非线性最小二乘问题P1
(4)
(3)令ri+1=ri(t)-IMFi(t);
(4)若‖ri+1‖2<ε1则迭代终止,否则返回步骤(2)。
上述步骤即为ASTFA的分解过程。本文将振动信号经ASTFA分解后得到若干个IMF分量,对每个IMF分量与原信号进行相关性分析,将相关性小的信号视为白噪声最稀疏匹配分解所得到的分量,相关性大的则视为原信号分量,最后将相关性大的分量进行叠加重构得到降噪后的信号。
2AKVPMCD原理
VPMCD是一种基于特征值之间可能存在一定的相互内在关系的一种模式识别方法。该方法为特征值选择变量预测模型(variable predictive model,VPM)的类型时,只能从L、LI、QI、Q这四种回归模型中选择其一,而这四种模型只能反映特征变量间的线性、二次、交互、二次交互的关系,当特征值在空间的数值分布具有一定的连续性和相关性时,其预测结果会出现一定的局部偏差,因此预测精度就会受到影响。为了克服上述缺陷,KVPMCD选择一种相关模型作为回归模型的补充来模拟局部偏差从而提高预测精度。KVPMCD只选择了相关模型的一种而忽略了其他几种相关模型对数据估计精度的作用,针对这个问题,本文提出了一种鱼群算法优化融合Kriging模型的AKVPMCD方法。
2.1子KVPM的建立
Kriging估计技术[13]的研究对象是空间预测问题,Kriging最初应用于地质统计学中。Kriging模型估计方法是一种方差最小的最佳无偏估计。Kriging模型由一个确定性的回归模型和一个随机函数构成,即

(5)
其中,f(x)为确定性的回归模型,包括零阶回归模型、一阶回归模型、二阶回归模型三种类型,也称之为确定性漂移;z(x)为描述空间相关性、连续性、各向异性、结构套合性的局部偏差的近似,有指数、线性、高斯等模型,也称之为涨落。


(6)
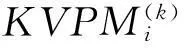

(7)
2.2人工鱼群智能算法对子KVPM权值矩阵的优化


(8)
通过模拟鱼的觅食、聚群、追尾、随机这几种典型行为,结合鱼对周围环境食物浓度的感知,选取“最优行为执行”的行为评价方式,来自主实现这些行为在不同时刻的转换,从而在搜索域进行寻优直至移动到全局最优位置,最后将所在最优位置参数解码为最优权值来组建最优权值矩阵。在保证优化精度的前提下,人工鱼群智能算法中的人工鱼群数和最大迭代次数越小,算法的收敛速度越快;移动步长越小算法的优化精度越高,移动步长越大优化精度越低,当移动步长较小时感知距离对优化精度影响不大[14]。因此,本文将人工鱼群数和最大迭代次数分别设置为100和50,将移动步长设置为0.1,经实验,算法能够达到所需优化精度。固定已设定参数再来交叉搜索,确定适当的拥挤度因子及感知距离。实验中,人工鱼群智能算法的具体参数如表1所示。

表1 人工鱼群算法参数设置
3基于ASTFA降噪和AKVPMCD的诊断方法
基于ASTFA降噪和AKVPMCD的滚动轴承故障诊断方法具体流程如图1所示。
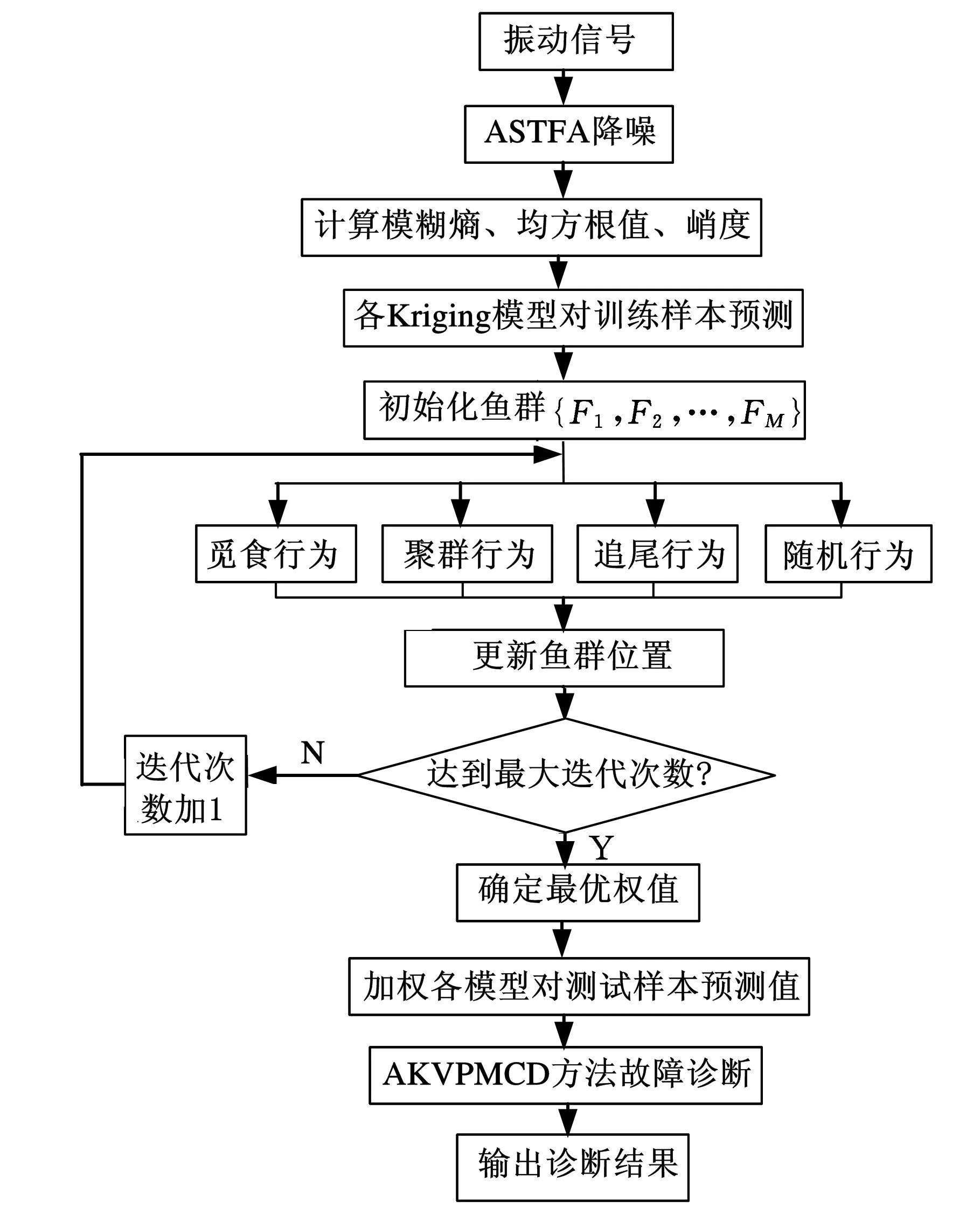
图1 基于ASTFA降噪和AKVPMCD的滚动 轴承故障诊断流程图
(1)一定转速下以采样频率fs对滚动轴承外圈故障、内圈故障、正常这几种状态进行采样,每种状态采集N个样本,得到滚动轴承的原始振动信号;
(2)利用ASTFA对原始振动信号进行分解,并对其进行相关系数法降噪处理,剔除主要由噪声信号分解得来的IMF分量后进行重构,得到有效的降噪信号。对每种状态下的降噪信号求模糊熵值、均方根值、峭度,组成特征值矩阵X。
(3)将样本矩阵X分为训练样本和测试样本,用上述五种Kriging模型对训练样本和测试样本分别进行预测,得到训练特征变量子KVPM预测值和测试特征变量子KVPM预测值。
(4)应用人工鱼群智能算法,将权值随机初始化为鱼群{F1,F2,…FM}的位置,以训练特征变量子KVPM预测融合值与训练特征变量真实值的误差矩阵的2-范数的倒数最大为目标函数,通过鱼群位置更新迭代进行全局寻优,从而得出最优权值组成的最优权值矩阵W(k)。

4应用
4.1仿真信号分析
本文用ASTFA降噪方法考察调幅调频仿真信号并与小波降噪、EMD降噪方法进行对比。仿真信号为
x(t)=2(1+0.5cos10πt)sin(90πt+
100t2)+3cos120πt+n(t)
(9)
仿真信号x(t)由一个调幅调频信号、一个余弦信号和白噪声信号组成。其中,噪声信号n(t)为在区间[-3,3]内随机分布的白噪声,如图2所示。
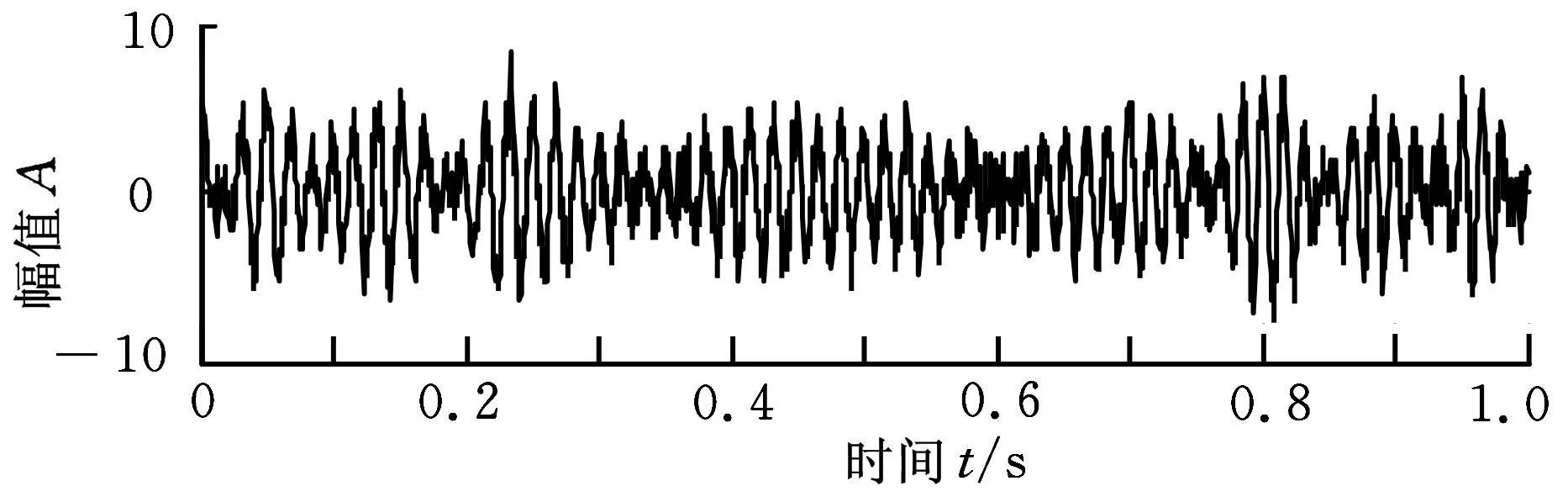
图2 原始含噪声信号
原始含噪信号分别经小波降噪(其中小波类型为haar,小波分解层数为2,软阈值均为3.645)、EMD降噪、ASTFA方法相关系数准则降噪。为了较好地对这三种方法的降噪效果进行衡量和比较,本文采用降噪后信号与原信号的相关系数R、信噪比SNR、降噪后信号与原信号的绝对偏差累积和S=∑|x(i)-x1(i)|以及能量误差E=∑(|x(i)-x1(i)|2)/∑x(i)2这四个指标作为降噪效果的评判标准,其中x(i)为无噪声信号,x1(i)为降噪后信号,三种降噪方法的评判指标值如表2所示。图3为三种降噪方法降噪后信号与原始信号的对比图。

表2 三种降噪方法效果的评判指标
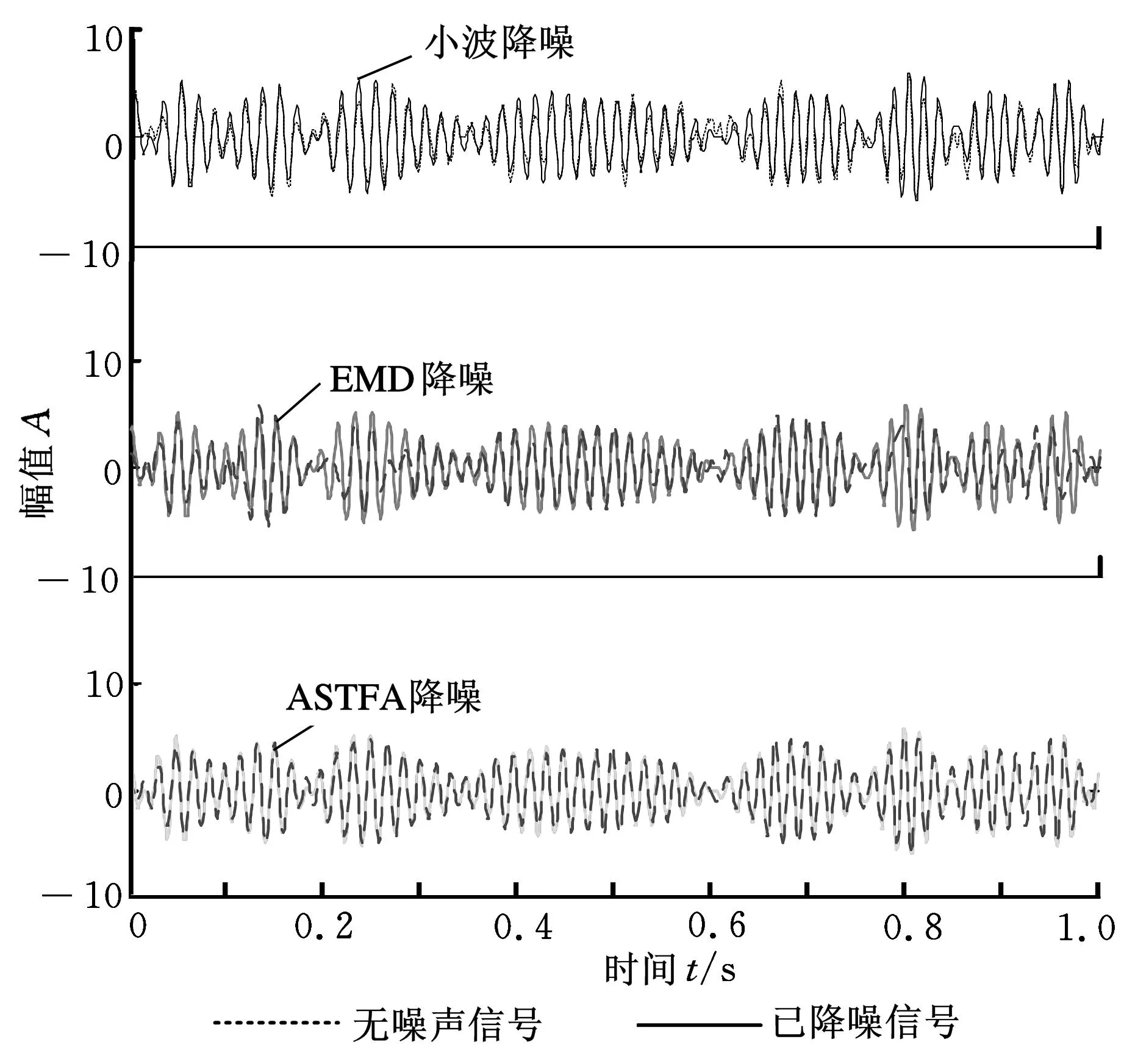
图3 三种方法降噪后信号与无噪声信号的比较
4.2实验信号分析
为了验证本文所提方法的有效性和优越性,在湖南大学滚动轴承故障实验台上对滚动轴承6307E型深沟球轴承进行了故障诊断实验分析[15]。通过激光切割分别加工宽0.15mm、深0.13mm的切槽来模拟内圈故障和外圈故障,由于实验条件的限制而未能在滚动体上设置故障。实验台调速电机为直流伺服电机,功率为600W。用磁性座底将振动加速度传感器固定在轴承座上,通过光电传感器采集转速信号,分别采集正常、内圈故障、外圈故障的振动加速度信号各100组,随机取其中的40组为训练样本,其余的60组为测试样本。实验中采样频率为8192Hz,转速为680r/min。图4为外圈故障状态的振动信号时域波形。
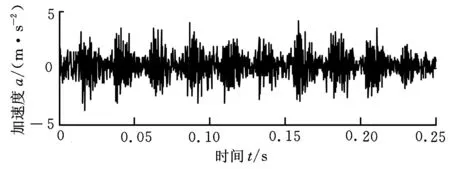
图4 外圈故障状态下滚动轴承振动信号时域波形
本文首先应用ASTFA方法对实验采集的滚动轴承振动信号进行分解,对滚动轴承每种工作状态下的振动信号分解得到8个IMF分量和一个残余量;然后采用相关系数准则将各工作状态下的振动信号分解得到的伪分量信号予以剔除,提取有用的IMF分量信号进行重构,从而达到对采集的振动信号降噪的效果;接着计算已降噪信号的模糊熵、均方根值、峭度(分别标记为X1,X2,X3)来组建特征值矩阵;最后应用AKVPMCD方法对滚动轴承的工作状态和故障类型进行分类识别。实验中,选取Kriging模型中的二阶回归模型与指数、高斯、线性、球体、样条这五种补充相关模型的组合分别通过样本训练建立各自的子KVPM模型。随后,随机初始化鱼群位置,再通过目标函数即食物浓度函数的设定,结合人工鱼群算法的全局寻优能力,求解各子KVPM的最优权值。外圈故障状态下的三个特征值X1、X2、X3的各子KVPM权值的寻优过程如图5所示(篇幅所限,省略其他两种工作状态的寻优过程图)。
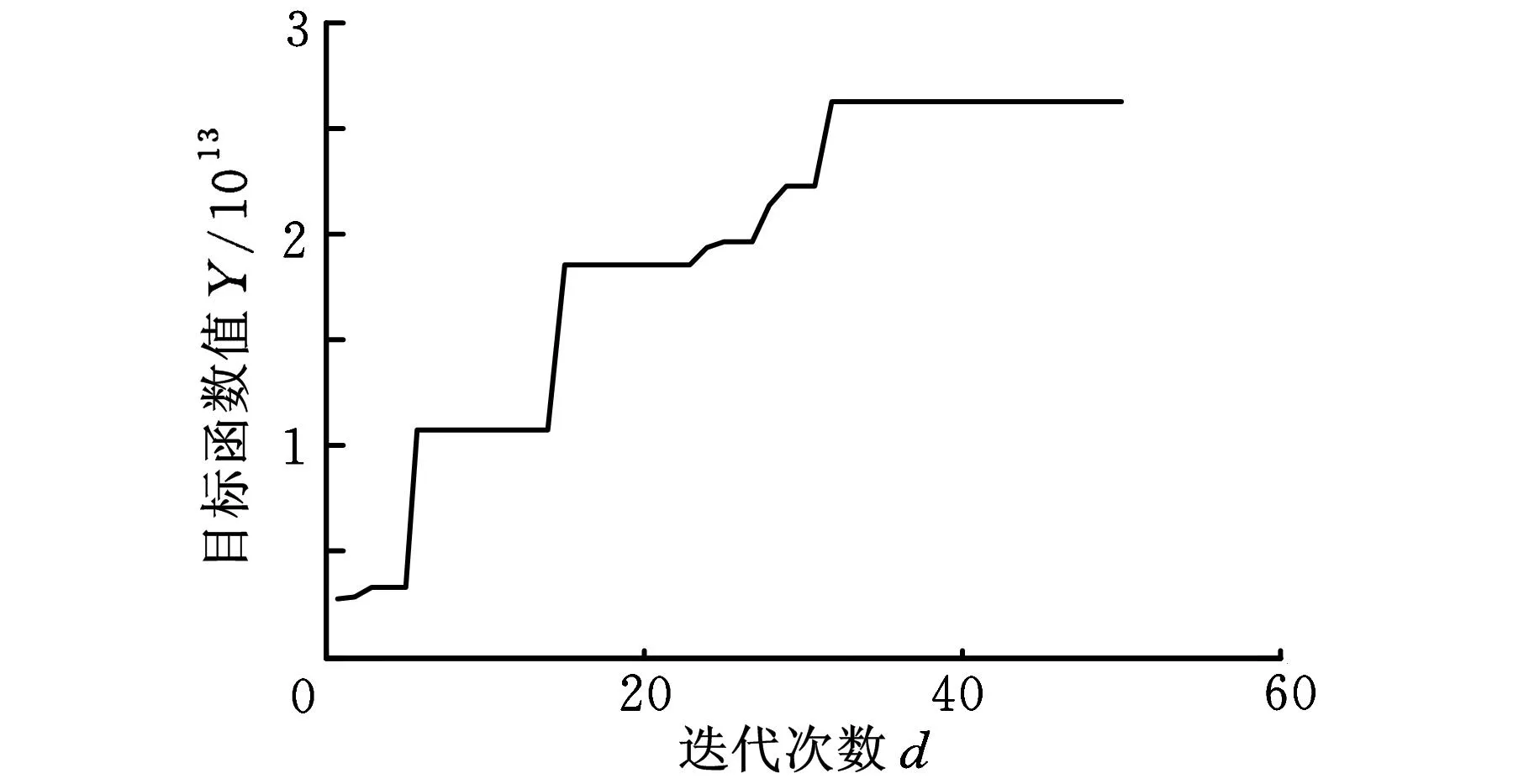
(a)X 1

(b)X 2

(c)X 3 图5 外圈故障状态下特征值的各模型权值优化过程
经人工鱼群智能算法优化后的滚动轴承各工作状态下三个特征值各子KVPM的最优权值如表3所示。
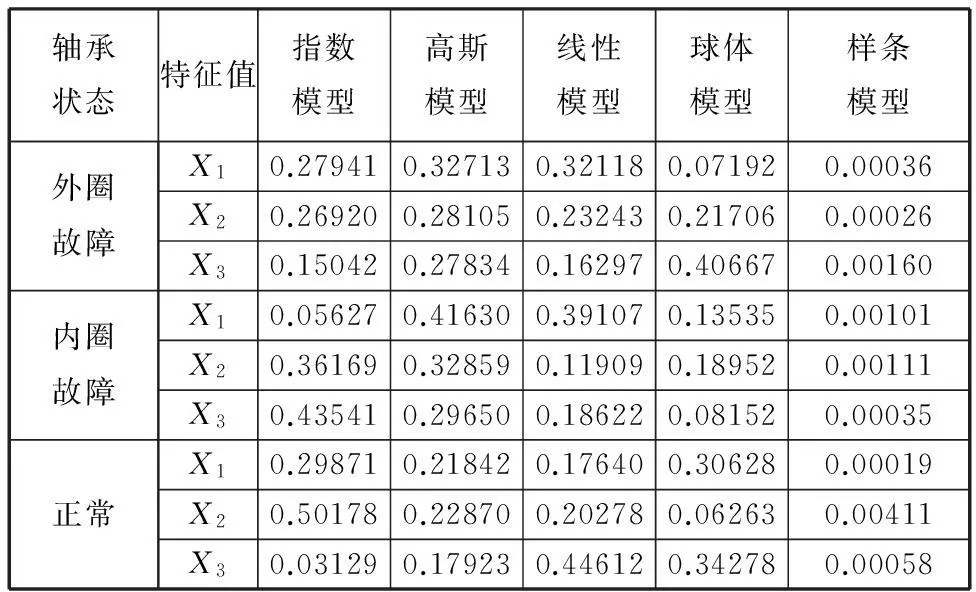
表3 滚动轴承各工作状态下三个特征值对应
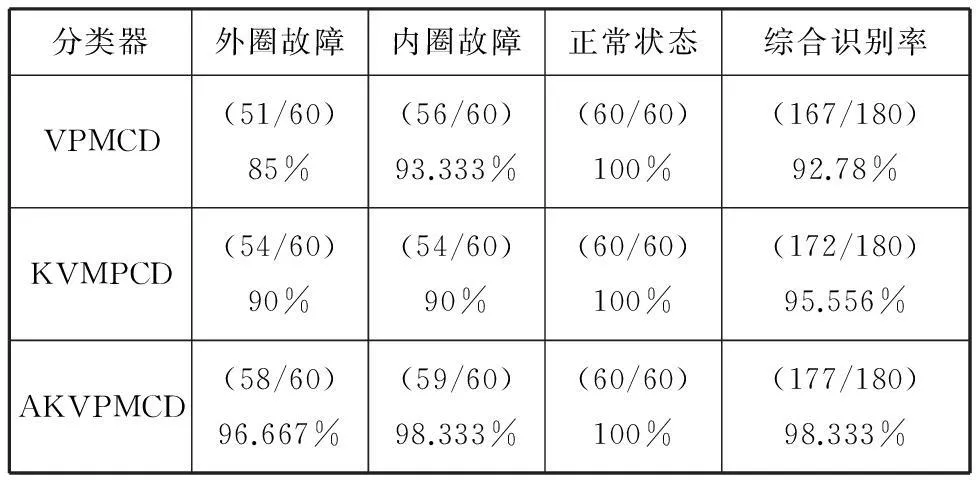
由上述滚动轴承各工作状态下三个特征值对应的最优权值加权融合各子KVPM对测试样本进行预测的预测值即可得到最佳预测值,再依据各类别工作状况的最佳预测值与何种类别测试样本真实值的误差平方和最小,则将其判别为哪类。AKVPMCD分类器与原VPMCD方法以及KVPMCD方法的分类结果对比如表4所示。
由表4可知,这三种分类器都能够将故障完全准确地识别出来,AKVPMCD与原VPMCD及KVPMCD分类器相比对故障类型的诊断精度有明显提高。由此可见,改进的AKVPMCD方法不仅有效且相比原来的VPMCD方法和KVPMCD方法诊断识别精度有较大幅度提高。
5结论
滚动轴承的故障振动信号往往表现出非线性、非平稳特征,且包含各种噪声,因而所提取的特征值分布情况比较复杂。本文将ASTFA降噪方法与经人工鱼群智能算法优化Kriging模型的AKVPMCD方法相结合应用于滚动轴承的故障诊断中,经研究得出以下结论:
(1)ASTFA方法能够有效地对滚动轴承振动信号进行降噪,无论是与小波降噪还是EMD降噪方法相比,在降噪效果上都有一定的优越性。
(2)Kriging模型是一种方差最小的无偏估计,能较精确地反映特征值的空间性和相关性,再结合人工鱼群算法的全局寻优能力,融合几种Kriging模型对数据进行预测估计,因而改进后的AKVPMVD方法能够更客观准确地对滚动轴承的工作状况进行分类识别。
(3)对滚动轴承外圈故障、内圈故障、正常状态的振动信号的分析结果表明,ASTFA降噪结合AKVPMCD可以准确、有效地对滚动轴承的工作状态和故障类型进行诊断,从而为滚动轴承的故障诊断提供了一种新的思路。
虽然ASTFA对振动信号具有良好的降噪效果,AKVPMCD具有很强的分类识别能力,但是ASTFA方法对其他类型的信号的降噪效果如何,如何对ASTFA方法进行改进使其对信号的分解和降噪效果进一步提升,以及如何找到比VPMCD方法中的回归模型和AKVPMCD方法中的Kriging模型更能客观、准确地反映机械故障机理的模型类型等问题仍值得进行更深层次的研究。
参考文献:
[1]Yi Weiguo,Duan Jing,Lu Mingyu.Double-layer Bayesian Classifier Ensembles Based on Frequent Itemsets[J].International Journal of Automation and Computing,2012,9(2):215-220.
[2]Chen Youshyang,Cheng Chinghsue.Hybrid Models Based on Rough Set Classifiers for Setting Credit Rating Decision Rules in the Global Banking Industry[J].Knowledge-based Systems,2013,39:224-239.
[3]Wang Huaqing,Chen Peng.Intelligent Diagnosis Method for Rolling Element Bearing Faults Using Possibility Theory and Neural Network[J].Computer & Industrial Engineering,2011,60(4):511-518.
[4]Fei Shengwei,Zhang Xiaobin.Fault Diagnosis of Power Transformer Based on Support Vector Machine with Genetic Algorithm[J].Expert Systems with Applications,2009,36(8):11352-11357.
[5]Raghuraj R,Lakshminarayanan S.Variable Predictive Models—a New Multivariate Classification Approach for Pattern Recognition Applications[J].Pattern Recognition,2009,42(1):7-16.
[6]杨宇,潘海洋,程军圣.基于Kriging函数的KVPMCD在滚动轴承故障诊断中的应用[J].中国机械工程,2014,25(16):2131-2136.
Yang Yu,Pan Haiyang,Chen Junsheng.Application of KVPMCD Based on Kriging Function in Rolling Bearing Fault Diagnosis[J].China Mechanical Engineering,2014,25(16):2131-2136.
[7]Verma H, Agrawal R K,Kumar N.Improved Fuzzy Entropy Clustering Algorithm for MRI Brain Image Segementation[J].International Journal of Imaging Systems and Technology,2014,24(4):277-283.
[8]Sayadi O, Shamsollahi M B. ECG Denoising and Compression Using a Modified Extended Kalman Filter Structure[J].IEEE Transaction on Biomedical Enginner,2008,55(9):2240-2248.
[9]Donoho D L,Johnstone M I.Adapting to Unknown Smoothness via Wavelet Shrinkage[J].Journal of the American Statistical Association,1995,90(12):1200-1224.
[10]Liu Junmin,Zhang Jiangshe.Spectral Unmixing via Compressive Sensing[J].IEEE Transaction on Geoscience and Remote Sensing,2014,52(11):7099-7110.
[11]Hou T Y,Shi Zuoqiang. Adaptive Data Analysis via Sparse Time-frequency Representation[J].Advances in Adaptive Data Analysis,2011,3(1/2):1-28.
[12]Hou T Y.Shi Zuoqiang.Data Driven Time-frequency Analysis[J].Applied and Computational Harmonic Analysis,2013,35(2):284-308.
[13]Bhattacharjee S,Mitra P,Ghosh S K.Spatial Interpolation to Predict Missing Attributes in GIS Using Semantic Kriging[J].IEEE Transaction on Geoscience and Remote Sensing,2014,52(8):4771-4780.
[14]王联国,施秋红.人工鱼群算法的参数分析[J].计算机工程,2010,36(27):169-171.
Wang Lianguo,Shi Qiuhong.Parameters Analysis of Artificial Fish Swarm Algorithm[J].Computer Engineering,2010,36(27):169-171.
[15]杨宇,潘海洋,程军圣.基于特征选择和RRVPMCD的滚动轴承故障诊断方法[J].振动工程学报,2014,27(4):629-636.
Yang Yu,Pan Haiyang,Chen Junsheng.The Rolling Bearing Fault Diagnosis Method Based on the Feature Selection and RRVPMCD[J].Journal of Vibration Engineering,2014,27(4):629-636.
(编辑苏卫国)
