基于差分进化和向量回归的四旋翼参数集员辨识

方旭，刘金琨

(北京航空航天大学 自动化科学与电气工程学院，北京100191)

0 引言

目前，垂直起降飞行器和无人机(UAV)的研究主要集中在航迹规划和跟踪两个方面，而对UAV的参数辨识研究并不多，特别是在飞行器参数集员辨识［1］方面缺少研究。在实际应用中飞行器系统的噪声统计特性很难确定，用统计类的辨识方法是行不通的，而集员辨识［2-4］却适合这种情况。集员辨识是在未知但有界噪声假设下进行的辨识，完成的工作是在参数空间中找到一个与量测数据和已知噪声界相容的可行解集，即参数空间的一个集合［5］，且集合中的每一个成员均为可行解。随着样本的增大，成员集范围逐渐缩小［6-7］。差分进化算法［8］在保留了遗传算法优点的同时，又避免了复杂的运算。跟踪微分器［9］通过积分提取微分信号，积分链式微分器可以有效地抑制噪声，而且可以直接估计系统高阶导数。

本文为了解决辨识模型回归矩阵奇异条件下的参数集员辨识问题，基于差分进化算法和非线性向量回归［10］，建立了逼近参数向量与误差向量的范数之间的函数关系模型，并用差分进化算法优化回归模型参数，避免了模型参数选择的盲目性。此方程的应用不要求回归矩阵非奇异，在奇异条件下也能进行集员辨识，扩大了适用范围。首先利用跟踪微分器由飞行器的位置和欧拉角信息估计其6个自由度的速度和加速度信息;然后，将整个系统分解为两个相对独立的子系统，简化辨识模型，利用差分进化算法对飞行器参数可行集的中心进行估计和建立回归函数;最后，根据得到的函数关系模型导出近似参数可行解集。

1 无人机系统动态模型

图1为四旋翼UAV受力图，其中Oxyz为惯性坐标系，飞行器有4个螺旋桨控制位置和欧拉角，l为飞行器半臂长，Fi(i=1，2，3，4)为螺旋桨推力形成的扭转力矩。

图1 四旋翼UAV结构图Fig.1 Structure of quadrotor UAV

利用欧拉-拉格朗日方法推导出UAV的动力学方程，其简化表达式如下:

式中:x，y，z分别为位置信息;θ，φ，ψ 分别为俯仰角、滚转角和偏航角;ai(i=1，…，10)为待辨识的参数，如表1所示，表中m为质量，c为比例系数，κi(i=1，…，6)为阻力系数，Ii(i=1，2，3)为转动惯量;ui(i=1，2，3，4)为虚拟输入，满足:

表1 待辨识的系统参数Table 1 Unknown parameters for identification

2 跟踪微分器和差分进化算法

四旋翼UAV的位置和欧拉角可以通过传感器来测量，设计了6个三阶跟踪微分器来分别获得飞行器位置、欧拉角的速度和加速度数据，三阶跟踪微分器设计如下:

其中s3+c3s2+c2s+c1=0满足Hurwitz稳定判据，μ是极小的正数，输入u是传感器测量到的位置或欧拉角信息，y1，y2为输出，方程(4)的Laplace变换为:

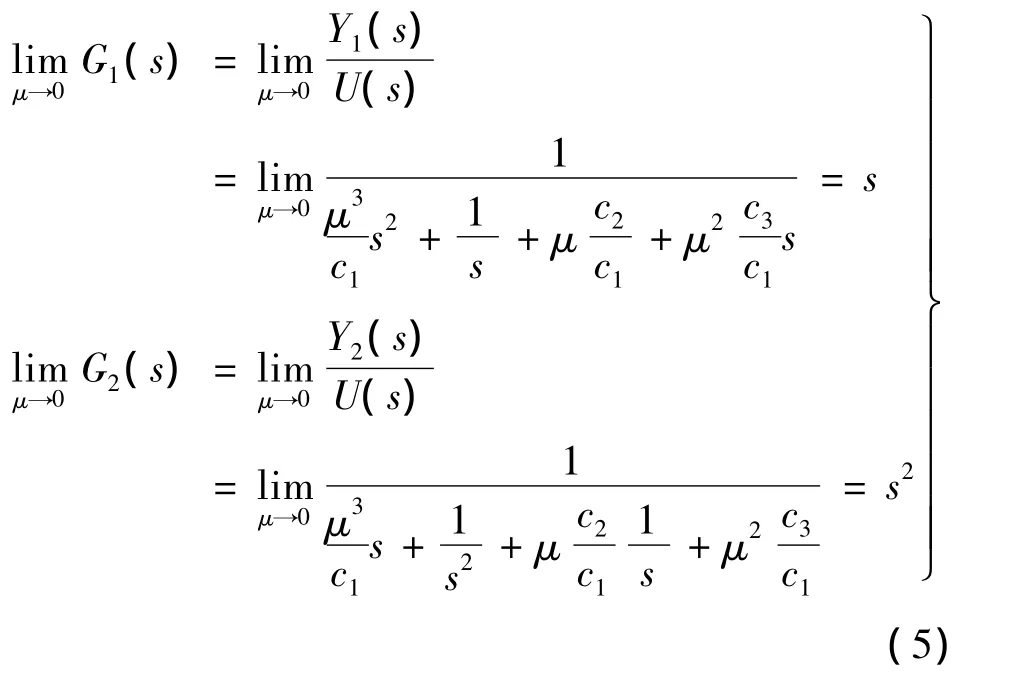
差分进化算法是比较成熟的智能算法，本文不做详细介绍，可参见文献［11］。差分进化算法的运行参数主要有:变异因子F、交叉因子CR、群体规模Z和最大迭代次数T。其收敛速度主要由F和CR决定:F较小时，易陷入局部极值;F较大时，收敛速度会减慢。为此，可以采用下式线性调整［12］变异因子F。

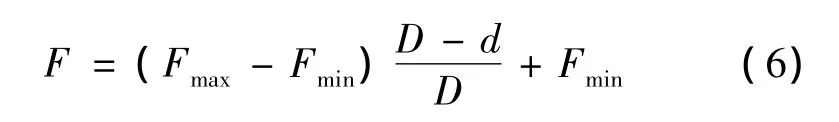
式中:d为当前进化代数;D为最大进化代数;Fmax和Fmin为选定的变异因子的最大、最小值。

CR越小，种群多样性减小，过早收敛;CR越大，收敛速度越大，但收敛变慢。同样，可以采用式(7)线性调整交叉因子CR:

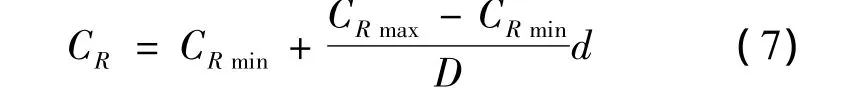
为了保证算法的性能，CRmax和CRmin应选取合理的值。随着进化代数的增加，F线性递减，CR线性递增，目的是希望改进的差分进化算法在搜索初期能够保持种群的多样性，到后期有较大的收敛速度。

3 飞行器系统分解和参数的中心估计

为了简化参数辨识的复杂度，将整个飞行器系统分解为两个独立的子系统，分别对其进行参数辨识。这样就成功地将一个高维的系统辨识问题降阶分解到两个低维的子系统上，避免了差分进化算法在进行高维优化时容易陷入局部最优的问题，同时也加快了系统的收敛速度。

两个独立的子系统(位置子系统(8)和姿态子系统(9))写成含有噪声的参数线性化回归模型形式m=Nθ+e如下:

式中:e∈R3为未知但有界的噪声;m∈R3为测量输出。位置子系统(8)记为ma=Naθa+ea，其中Na∈R3×4，θa∈ R4;而姿态子系统(9)记为 mb=Nbθb+eb，其中Nb∈R3×6，θb∈R6。系统分解后就可以分别对子系统进行集员辨识，下面以其中任意一个子系统m=Nθ+e为例介绍中心估计方法［13］。假设得到k组数据，记:

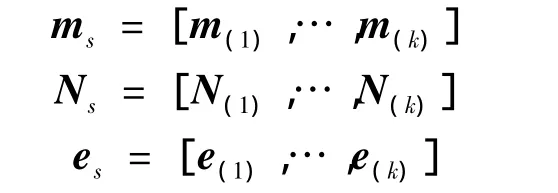
可得ms=Nsθ+es，集员辨识常用最小二乘法进行参数的中心估计，但要求非奇异，限制了适用范围。

因此，采用改进差分进化算法进行中心估计，辨识误差指标选为:

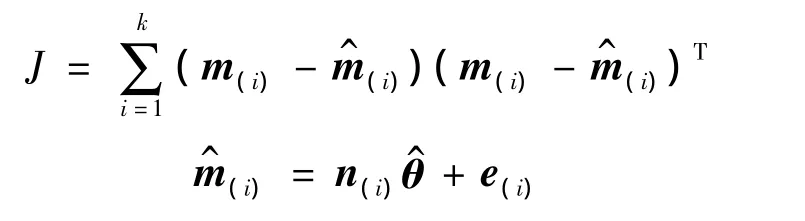
图2为集员辨识中心点估计流程图。

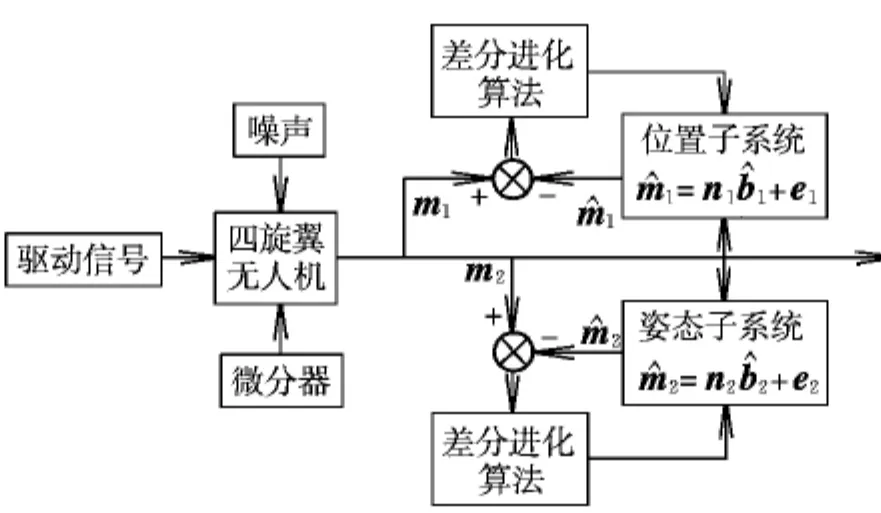
图2 集员辨识中心点估计流程图Fig.2 Flow chart of set membership identification center estimation

4 基于差分算法和向量回归的集员估计

以飞行器系统中任意一个子系统m=Nθ+e为例介绍集员辨识方法，与文献［15-16］不同，本文采用差分进化算法对回归模型参数进行优化，并且给出适合四旋翼参数集员辨识的加权方法。e∈R3是有界的，满足Ve∈R3是l2范数意义下有界的，即为对角加权矩阵，d∈R为误差界限。由上可得与回归模型、测量输出、误差界限相容的集合为:

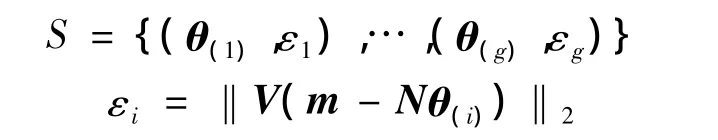
式中:向量θ(i)(i=1，…，g)为参数空间中的点。根据样本集S建立逼近误差向量l2范数ε∈R与θ之间的函数关系的模型:

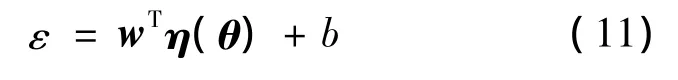
式中:η(·)为从低维参数空间θ∈Rp到高维特征空间Rq(q＞p)的非线性映射;w∈Rq为权重向量;b∈R为偏置量。为了得到w，b，依据非线性回归结构风险最小化原则，将其学习过程转化为优化问题如下:

式中:i=(1，…，l);Bi为松弛变量;γ为惩罚系数。利用拉格朗日方程求解最佳参数:

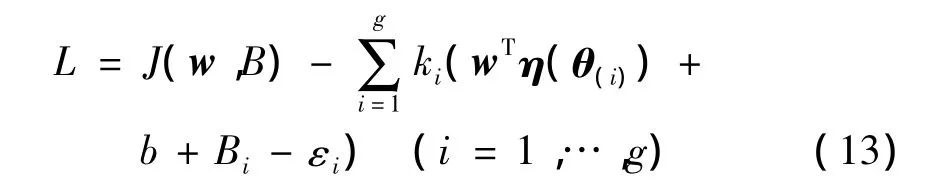
ki∈R为拉格朗日乘子，求解最优参数，得到下列矩阵方程:

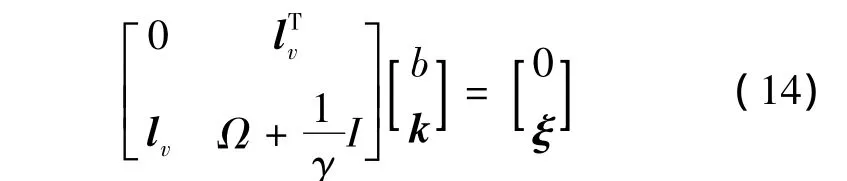
式中:ξ =［ε1，…，εg］;lv=［1，…，1］;k=［k1，…，kg］;Ω∈Rg×g为矩阵中的元素，Ωij= η(θ(i))Tη(θ(j))(i，j=1，…，g)，根据梅塞条件存在核函数满足式(14)。本文选取核 函数为σ2}(i，j=1，…，g)，其中 σ 为核函数宽度系数，解矩阵方程得到b，k，最终得到最优方程解:

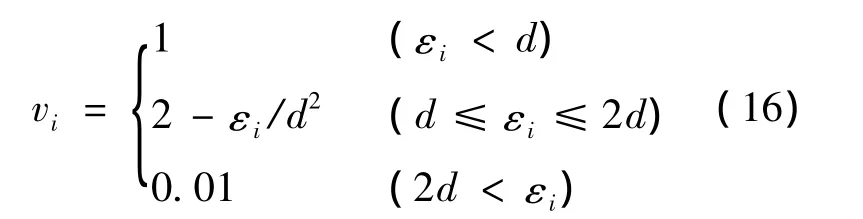
那么优化问题式(12)变为:

同样利用拉格朗日方程求解最佳参数，可得到最终模型形式:

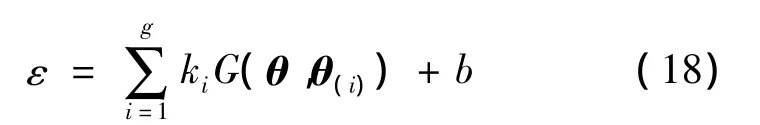
因此集员估计可行解公式为:

假设得到Tk组采样数据m，N，每组数据得到一个可行解:

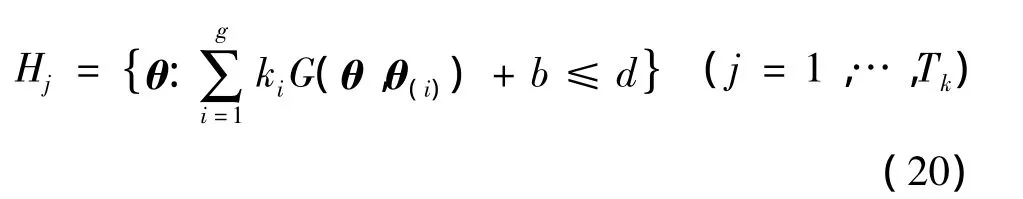
如果真实参数的先验信息θ*∈Θ0，Θ0是参数空间的有界集合。那么，系统参数集员估计的可行解为Θ0与Hj的交集，即:

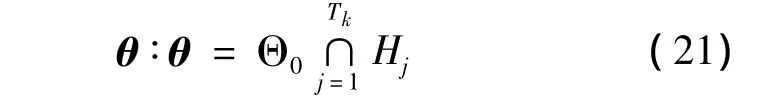
5 仿真实验与分析

改进的差分进化算法参数设置为:Fmax=0.9，Fmin=0.4，CRmax=0.9，CRmin=0.3，Z=80，D=500;跟踪微分器参数设置为:c1=200，c2=140，c3=22，μ=0.01;飞行器输入为:u1=10 sin(t)，u2=10 cos(t)，u3=10 sin(t)，u4=10 cos(t);系统物理参数为:a1=0.465 1，a2=0.051 2，a3=0.055 8，a4=0.051 2，a5=0.195 3，a6=0.033 2，a7=0.198 4，a8=0.031 7，a9=0.463 4，a10=0.013 1;最优参数σ=0.025，γ=1e－4;根据测量输出信号的变化范围，取噪声向量元素的界限为0.03。集员参数辨识结果如表2所示。

表2 集员参数辨识结果Table 2 Results for UAV set membership identification

图3为系统6个自由度的幅值变化和系统噪声。图4为两个子系统改进差分进化算法参数中心估计的辨识误差指标收敛过程。

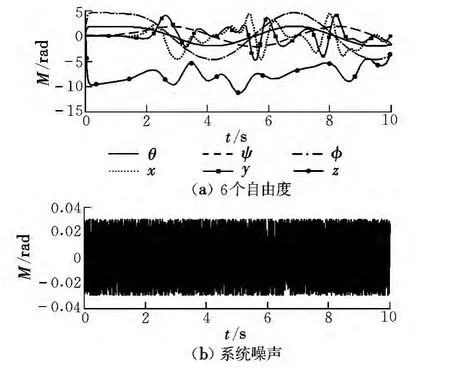
图3 6个自由度幅值变化和噪声Fig.3 Amplitude change of 6 degress and noise

图4 子系统辨识指标Fig.4 Identification index of subsystem

从以上图表可以发现，高阶积分链式微分器可以精确地跟踪UAV的位置和欧拉角信息，并且得到速度和加速度数据。在噪声环境下，改进差分进化算法能很好地进行参数中心点估计和优化回归函数参数。在集员区间估计方面，参数 a1，a4，a5，a7，a9的估计区间较小，其估计结果可信度高，而剩下的5个参数估计区间较大，其结果只可作为参考，因为这5个参数数量级较小，即使在参数变化较大的情况下引起的误差仍然较小，依然满足可行解方程，所以区间估计较大。

6 结束语

本文仅基于UAV位置和欧拉角信息，利用跟踪微分器得到速度和加速度数据，将复杂系统分解为两个独立的子系统进行辨识，减轻了辨识的工作量。利用非线性向量回归方法建立逼近参数向量与误差向量的范数之间的函数关系模型，用差分进化算法进行参数中心点估计和优化回归函数参数，避免参数选择的盲目性。为了进一步完善算法，对样本数据进行加权处理。给出了一种四旋翼参数的集员估计方法，为集员辨识在飞行器上的应用提供了一种新的思路。

［1］ Milanese M，Vicino A.Optimal estimation theory for dynamic system with set membership uncertainty:an overview ［J］.Automatica，1991，27(6):997-1009.

［2］ Cheng M F，Yurkovich S，Passino K M.An optimal volume ellipsoid algorithm for parameter set estimation［J］.IEEE Transactions on Automatic Control，1993，38(8):1292-1296.

［3］ Kosut R L，Lau M，Boyd S.Set-membership identification of systems with parametric and nonparametric uncertainty［J］.IEEE Transactions on Automatic Control，1992，37(7):929-941.

［4］ Fogel E，Huang Y F.On the value of information in system identification¯bounded noise case［J］.Automatica，1982，18(2):229-238.

［5］ Deller J P.Set membership identification in digital signal processing［J］.IEEE ASSP Magazine，1989，6(10):4-20.

［6］ Veres SM，Norton JP.Structure identification of parameter-bounding models by use of noise－structure bounds［J］.International Journal of Control，1989，50(2):639-649.

［7］ Broman V，Shensa M J.A compact algorithm for the intersection and approximation of N-dimensional polytopes［J］.Mathematics and Computers in Simulation，1990，32(5):469-480.

［8］ Chakraborty U K，Das S，Konar A.Differential evolution with local neighborhood［C］//2006 IEEE Congress on Evolutionary Computation.Piscataway，N.J.IEEE，2006:2042-2049.

［9］ Wang X H，Chen Z Q，Yuan Z Z.Design and analysis for new discrete tracking-differentiators［J］.Applied Mathematic¯A Journal of Chinese Universities，2003，18(2):214-222.

［10］ Suykens J A K，Vandewalle J.Least squares support vector machine classifiers ［J］.Neural Processing Letters，1999，9(3):293-300.

［11］ Chang W D.Parameter identification of Chen and Lü systems:a differential evolution approach ［J］.Chaos，Solitons ＆ Fractals，2007，32(4):1469-1476.

［12］ Das S，Konar A，Chakraborty U K.Two improved differential evolution schemes for faster global search［C］//Proceedings of the 2005 Conference on Genetic and Evolutionary Computation.New York，USA，ACM，2005:991-998.

［13］ Bingül Z，Karahan O.Dynamic identification of Staubli RX-60 robot using PSO and LS method［J］.Expert Systems with Applications，2011，38(4):4136-4149.

［14］ Tang H H，Xue ST，Fan CX.Differential evolution strategy for structural system identification ［J］.Computers and Structures，2008，86(21):2004-2012.

［15］ Keesman K J，Stappers R J J.Nonlinear set-membership estimation:a support vector machine approach ［J］.Journal of Inverse and Ill-Posed Problems，2004，12(1):27-41.

［16］柴伟.集员估计理论、方法及其应用［D］.北京:北京航空航天大学，2010.