基于动态势场法的最优一致性避障算法研究

孙景亮，刘春生，史浩明

(南京航空航天大学 自动化学院，江苏 南京210016)

0 引言

避障问题是研究多智能体飞行器协同控制不可忽视的关键问题，这将直接影响飞行器能否顺利完成既定任务以及适应复杂环境的能力。近年来，针对飞行器协同一致性以及避障的研究不胜枚举，其主要应用工具就是图论。它将多飞行器系统看作网络拓扑［1］，这对多智能体系统的研究具有指导意义。同时，考虑到续航能力、经济性、实时性等重要指标的要求，最优一致性算法得到广泛发展［2-3］。针对复杂环境下的最优避障，其方法主要是两类:一是分别设计最优一致性控制器和避障控制器［4］，该方法应用广泛且简单实用，但并不能保证系统的全局最优，即飞行器的避障过程不是最优化的;二是将避障函数直接设计在优化性能指标函数中［5］，从而保证了飞行器的全局最优。这两种方法均未过多考虑传统人工势能场的缺点，即飞行器易陷入局部极值。文献［6］采用选择速度避障的方法，将飞行器的速度信息用于避障，有效降低了陷入局部极值的可能性，但该方法只针对特定的三种模式下的避障，因而不具有普遍性。

传统人工势能场避障函数是利用对飞行器的排斥力迫使其远离障碍物，但当飞行器处于势能场向量的相反方向时，势能场的排斥力很容易抵消飞行器的速度，从而使飞行器陷入局部极值或瞬间失速的状态，这对于飞行器而言，无疑是致命弱点。

针对以上分析，本文提出基于动态势场法的最优一致性避障算法，使势能场向量根据飞行器距离障碍物的位置信息和速度信息而变化，这样势能场向量和飞行器速度向量的合力，迫使飞行器平滑绕过障碍物，既解决了飞行器陷入局部极值的问题，又能够避免接近障碍物时引起的振荡，同时可以保证系统的全局最优。

1 图论

多智能体之间的通讯拓扑结构可以用一个图G=(V，E)来表示。其中:V表示图G的有限非空顶点集合V={1，2，…，n};E表示图的有限边集合，E={(i，j)|i，j∈V，i≠j}，(i，j)表示智能体 i和 j之间的通讯，i=1，2，…，n。在图 G 中，若(i，j)∈E≠(j，i)∈E，则称该图为有向图，否则为无向图。

本文假设智能体之间的网络拓扑结构为无向图，假设存在5个智能体，其网络拓扑结构如图1所示。

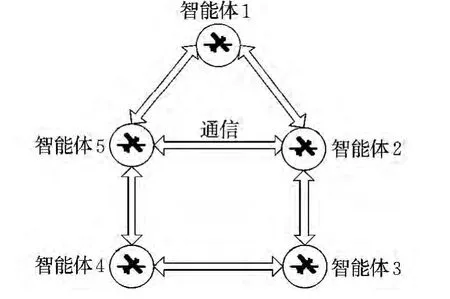
图1 智能体通信拓扑结构Fig.1 Communication topology of agents

图G的拉普拉斯矩阵L=D(G)－A(G)。其中:度矩阵D(G)=diag(d(i))，d(i)为图G中与顶点 i相关联边的数目;邻接矩阵 A(G)=［aij］，aij为连接顶点i与顶点j的边数。拉普拉斯矩阵L存在如下性质:0是矩阵L的一个特征值，向量1是特征值0所对应的特征向量［7］。

2 问题描述

用一组单积分器动态系统来描述多智能体系统，其状态空间表达式为:

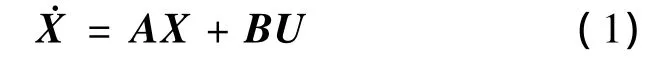
其中:

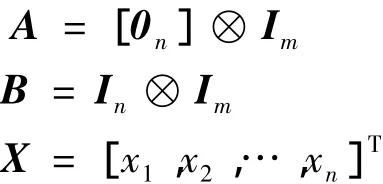
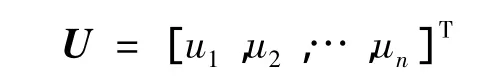
式中:xi∈ Rm，ui∈ Rm(i=1，2，…，n)分别表示智能体i的位置和控制输入;⊗表示矩阵的Kronecker积;0n表示n维零矩阵;Im，In分别表示m维和n维单位矩阵。

定义误差动态方程为:

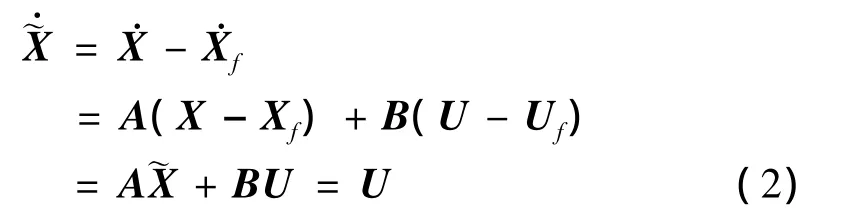
式中:Xf∈Rm表示飞行器终端状态;Uf为终端控制输入。由图论拉普拉斯矩阵性质可得0nm×1，即终端状态Xf为常数，终端控制输入Uf为零。

3 避障函数

假设障碍物可表述为矩形(x0±v1，y0±v2)，其中(x0，y0)为矩形中心，v1，v2∈R+。则围绕该矩形障碍物所形成的势能场向量可表述为:

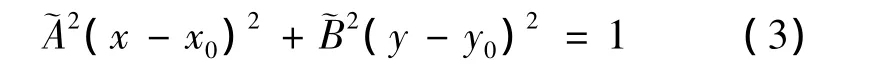
其中:

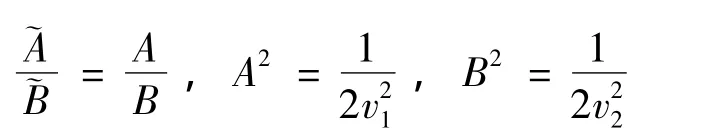
引理［8］:在椭圆簇上任意一点(x，y)沿着椭圆轨迹顺时针旋转的轨迹方程为:

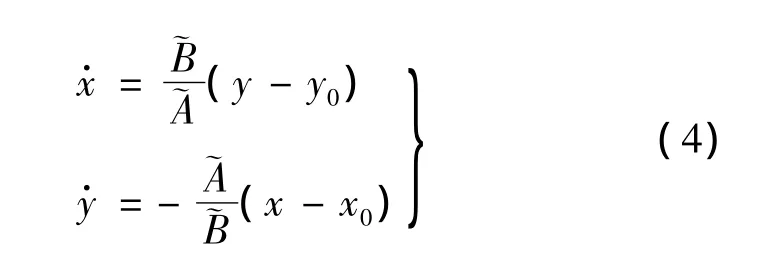
如图2所示，飞行器与障碍物中心连线和水平方向的夹角为χi=atan 2(y0－yi，x0－xi)，函数atan 2计算两点形成的斜率角度，取值范围atan 2(y，x)∈［－ π，π］。

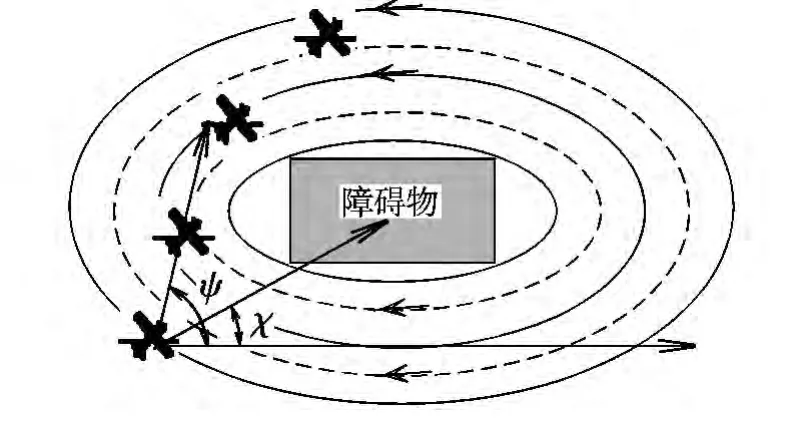
图2 动态势能场避障示意图Fig.2 Obstacle avoidance in dynamic potential field

假设旋转势能场向量可以表示为:

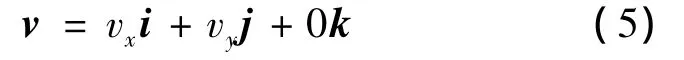
则由旋转轨迹方程式(4)得:

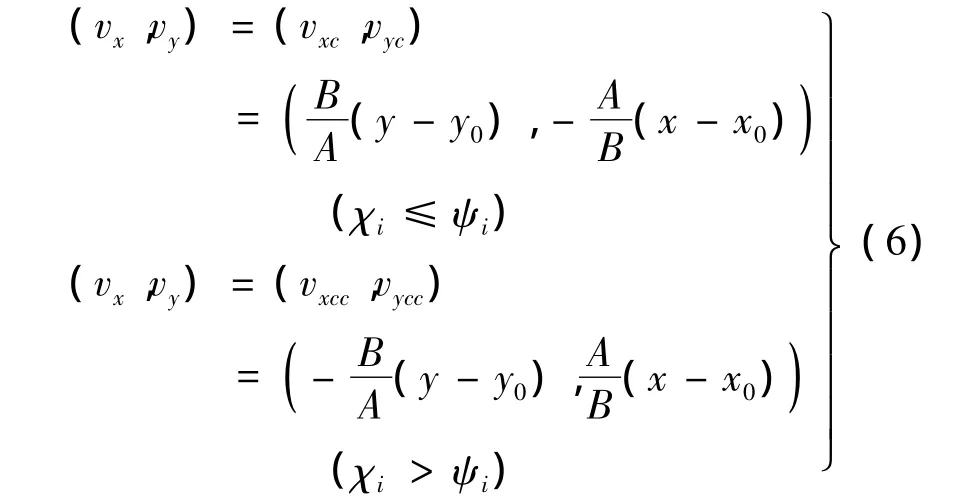
式中:(vxc，vyc)，(vxcc，vycc)分别表示势能场向量顺时针旋转向量和逆时针旋转向量。

为保证势能场向量随着飞行器与障碍物距离的减小而增大，对势能场向量进行如下改造:

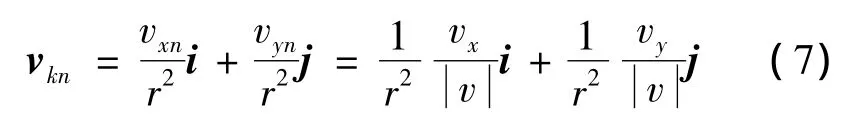
其中:

因此障碍物周围势能场向量可以表示为:

4 控制器设计

最优一致性避障问题可表述为以下最小化性能指标:

假设最优代价函数

则Hamilton函数可表示为:

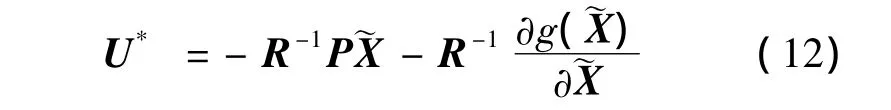
矩阵P满足Riccati方程:

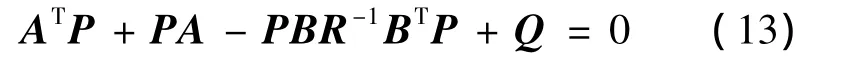
将矩阵 A，B，R，Q 带入式(13)，解得:

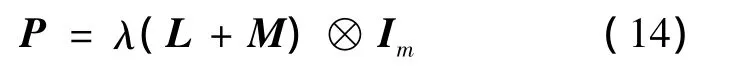
所以最优控制

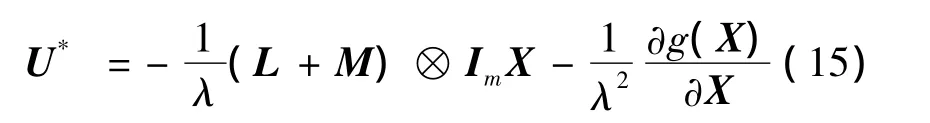
令 ∂H/∂U=0，可得:

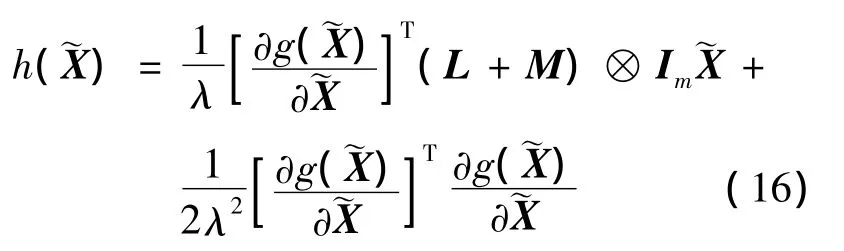
由式(16)可知，总可以找到一个足够小的权重矩阵M和适当的权重系数λ，使得避障势能函数

5 稳定性分析

由文献［9］关于非二次型性能指标的最优控制问题证明可以得出:非线性系统Hamilton-Jacobi-Bellman(HJB)方程的稳态解是一个李雅普诺夫函数，这样不仅保证了系统的稳定性，而且满足最优条件。因此，选取李雅普诺夫函数证明系统的稳定性:

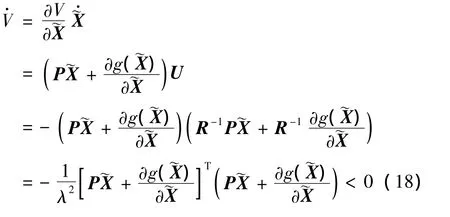
6 仿真验证

多智能体系统拓扑结构如图1所示。该拓扑结构是无向连通图，则拉普拉斯矩阵可以定义为:

假设5个智能体初始位置分别为(5，－6)，(8，8)，(－6，－3)，(－2，－6)和(－2，4)，权值矩阵 M=0.85In，λ=5.24。本文分别对智能体群在无障碍物、存在单个障碍物和多个障碍物的情况下进行仿真验证。

智能体在无障碍物情况下飞行，飞行轨迹和控制输入如图3～图5所示。

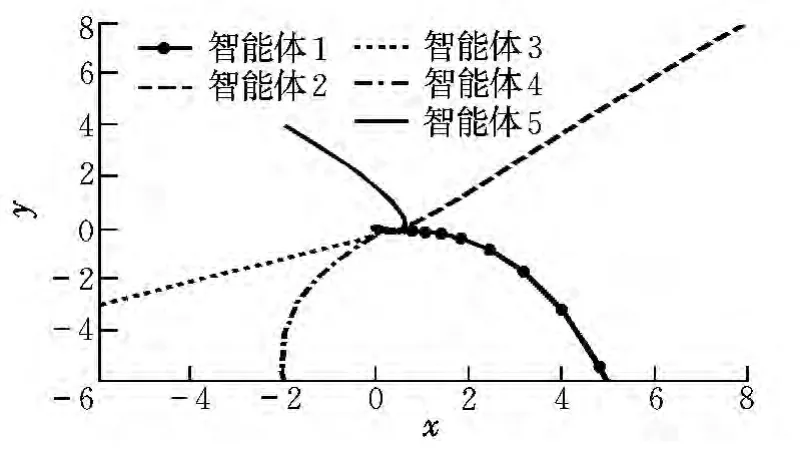
图3 无障碍物一致性飞行轨迹Fig.3 Consensus trajectories of five agents without obstacles

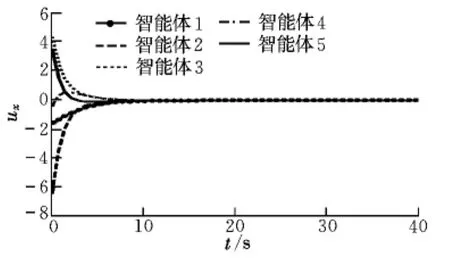
图4 x轴控制输入Fig.4 Control input on x-axis

图5 y轴控制输入Fig.5 Control input on y-axis

由飞行轨迹图和控制输入可以得出，飞行器最终汇聚于某一点，设计的最优控制律使系统达到一致性要求，控制输入逐渐减少为零。

假设飞行轨迹上存在一个障碍物，位置坐标为(4±1，4±0.5)，轨迹如图6所示。

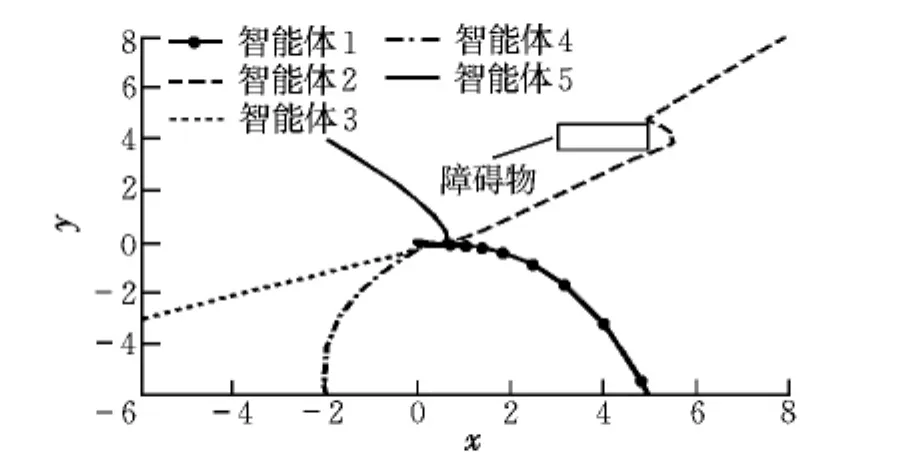
图6 单个障碍物避障轨迹Fig.6 Trajectories of agents with a single obstacle

从仿真图可以验证动态势能场避障函数的有效性，能够使飞行器顺利躲避障碍物，达到系统整体的一致性要求。

假设系统飞行轨迹上存在3个障碍物，位置坐标分别为(3±1，3±0.5)，(－3±1，－2±0.5)，(6±0.5，6±1)，飞行轨迹如图7所示。

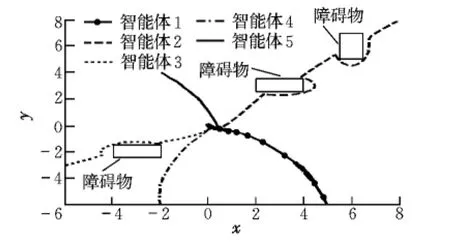
图7 多个障碍物避障轨迹Fig.7 Trajectories of agents with multiple obstacles

仿真结果表明，在存在多个障碍物的复杂环境中，飞行器依然能够有效躲避障碍物，实现一致性要求，达到期望的目标。

7 结束语

本文对多智能体飞行器的最优一致性避障问题进行了研究，仿真结果表明所设计的算法能够有效躲避障碍物，实现一致性。

本课题待解决的问题还有:多个距离较近障碍物的情况，这种情况下动态势能场会相互影响;飞行器存在通信时滞问题，这必将降低系统的一致性，同时影响飞行器的避障过程。

［1］ Olfati-Saber R，Murray R M.Consensus problems in networks of agents with switching topology and time-delays［J］.Automatic Control，IEEE Transactions on，2004，49(9):1520-1533.

［2］ Semsar-Kazerooni E，Khorasani K.An LMI approach to optimal consensus seeking in multi-agent systems［C］//American Control Conference，ACC'09.St.louis，Mo，USA:IEEE，2009:4519-4524.

［3］ Cao Y，Ren W.Optimal linear-consensus algorithms:an LQR perspective［J］.Systems，Man，and Cybernetics，Part B:Cybernetics，IEEE Transactions on，2010，40(3):819-830.

［5］ Wang J，Xin M.Optimal consensus algorithm integrated with obstacle avoidance［J］.International Journal of Systems Science，2013，44(1):166-177.

［6］ Jenie Y I，Van Kampen E J，de Visser CC，et al.Selective velocity obstacle method for cooperative autonomous collision avoidance system for UAVs［C］//Guidance，Navigation，and Control(GNC)Conference.Boston，MA:AIAA，2013:4627-4646.

［7］ 潘欢.二阶多智能体一致性算法研究［D］.长沙:中南大学，2012.

［8］ Sabir D，Wu Q.Cooperative tracking control and obstacles avoidance for single-integrator dynamics［C］//Control Conference(CCC)，2013 32nd Chinese.IEEE，2013:7162-7167.

［9］ Bernstein D S.Non-quadratic cost and nonlinear feedback control［J］.International Journal of Robust and Nonlinear Control，1993，3(3):211-229.