无人机地面操纵转弯特性分析与计算研究

邱东海，马伍元，段镇，周凌，贾宏光，杨洪波

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春130033;2.中国科学院大学，北京100039)

0 引言

随着无人机在军事领域的广泛应用，对无人机地面运行特性的要求也日益增高。例如，为了适应未来严酷的战场条件，要求无人机拥有在简单修复的跑道或泥土道面起降的能力［1］。然而，在高速滑跑过程中，无人机常有因操纵不当而导致侧滑或者侧翻等危险事故发生。因此，研究无人机地面运动品质及转弯性能，对于提高无人机的安全性及机动性，具有十分重大的工程意义［2-3］。

针对大型飞机的地面操纵问题，国内外基于模型简化或利用多体动力学软件开展了一些研究。Khapane［4］利用SIMPACK研究了起落架弹性对地面操纵的影响。顾宏斌［5］采用无滑动轮胎模型建立了飞机地面操纵的数学模型。钱小妹［6］在不考虑飞机受外界力情况下，利用Adams/Aircraft研究了飞机匀速滑跑时的转弯特性。张明等［7］给出了多轮起落架飞机前轮转向模型，但忽略了气动力的影响。朱天文［8］在考虑机轮状态为定值的前提下，计算了飞机地面操纵的转弯性能。以上研究可以看出:转弯性能研究主要基于虚拟样机仿真，通过试凑不同前轮操纵角验证飞机是否发生侧滑或者侧翻，从而给出操纵角的允许范围。该方法有一定的局限性，无法适用于真机滑跑时的操纵转向。因此，如何准确求解无人机滑跑时的瞬态参数，并在理论上给出无人机转弯性能的计算方法，对飞机的滑跑操纵具有重要意义。

本文在考虑轮胎侧偏特性、气动力和发动机推力情况下，针对某小型无人机建立了该飞机的地面滑跑动力学模型，求解了无人机的瞬态参数。接着建立了操纵转弯的数学模型，通过数字仿真计算了无人机在各滑跑速度下所允许的极限操纵角和最小转弯半径。

1 地面滑跑动力学建模

本小型无人机采用前轮操纵转向方式，前起落架装载了转向舵机，该方式纠偏控制响应快，不产生额外阻力。滑跑过程受力如图1所示。图中:θl为前轮操纵角;θn为前轮速度方向与机体纵向轴线夹角;βn，βml，βmr分别为前轮与左右主轮的侧偏角;an为前轮到重心的距离;am为主轮到重心的距离;bw为主轮距;Py为侧偏距;ψ为偏航角;Vm为空速;u，v分别为机体坐标系下x轴和y轴的速度;F，Q，P分别为三个机轮的侧向力、滚动阻力和支反力;下标n，ml，mr分别为前轮和左右主轮。

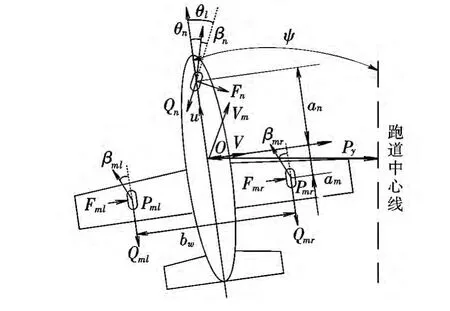
图1 无人机地面滑跑受力示意图Fig.1 Forces applied on UAV during ground runing

1.1 地面作用力

飞机空中飞行的六自由度非线性模型研究已较为成熟，文献［9］详细给出了飞行器在空中运动的数学模型。本文在飞行器空中飞行阶段非线性数学模型的基础上，加入地面受力状态和运动特点。在机体坐标系下地面作用力可表示为:

1.1.1 地面对机轮的侧向力和滚动阻力

对于弹性轮胎，地面侧向力作用在转动轮胎前进方向的后侧，因此弹性轮胎在该侧力的作用下，相对机轮有扭角β，称为侧偏角(其计算在下文中介绍)。侧向力F与侧偏角的关系是一个非线性函数，当β很小时可近似认为存在以下线性关系:

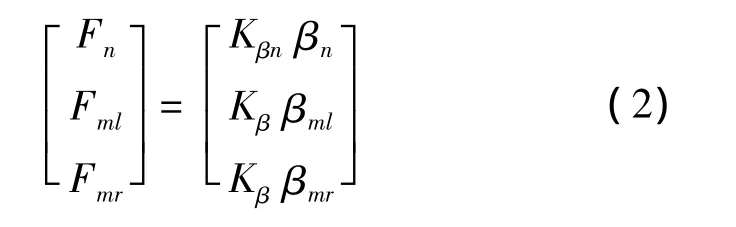
式中:Kβn，Kβ分别为前轮和主轮的侧向刚度。

不考虑施加刹车，机轮在地面的滚动摩擦阻力为:

式中:μ为滚动摩擦系数。

1.1.2 地面对机轮的支反力

确定无人机的三轮支反力有两种:一是根据运动方程的已知条件求解;二是根据各起落架的压缩量和压缩速度，结合起落架缓冲器的机械特性求解。考虑简化模型计算，本文忽略了起落架的弹性，采用第一种方式，定义滑跑过程中俯仰角和滚转角为零，飞机三轮未离地，得到法向力、滚转力矩和俯仰力矩三个平衡方程，从而推出支反力P关于侧向力F的解析表达式。

法向力平衡方程、滚转力矩平衡方程和俯仰力矩平衡方程分别为:

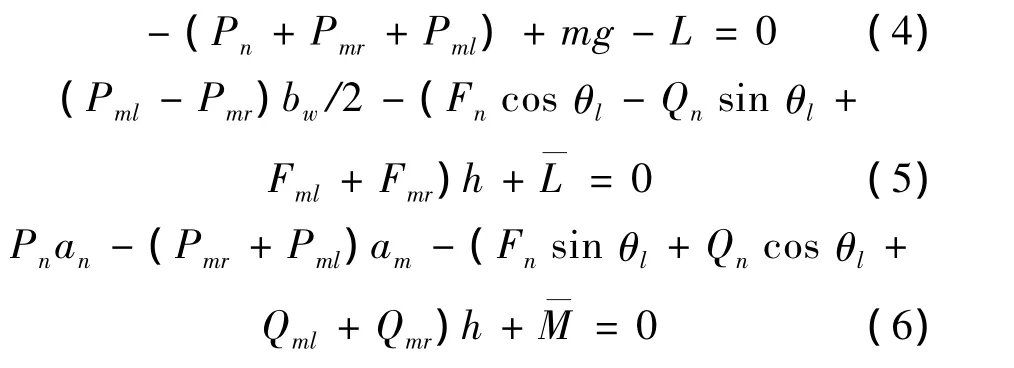
1.2 动力学方程

根据无人机地面滑跑特点，得到无人机在机体系下的质心移动动力学方程:

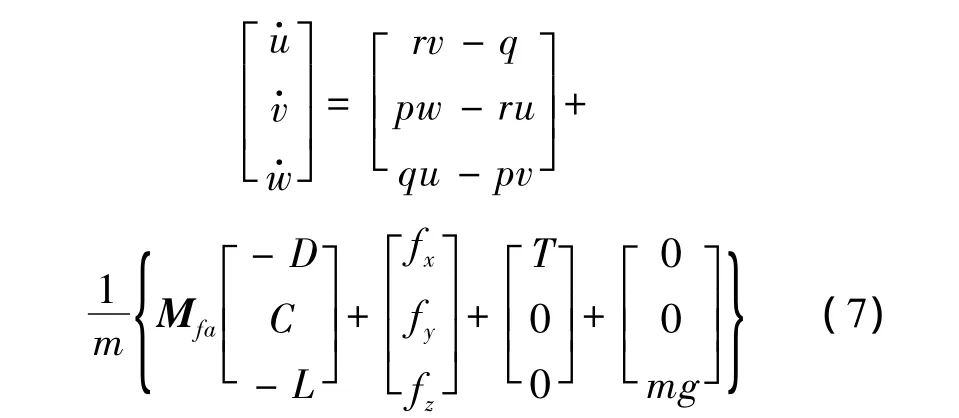
无人机绕机体各轴旋转的动力学方程为:

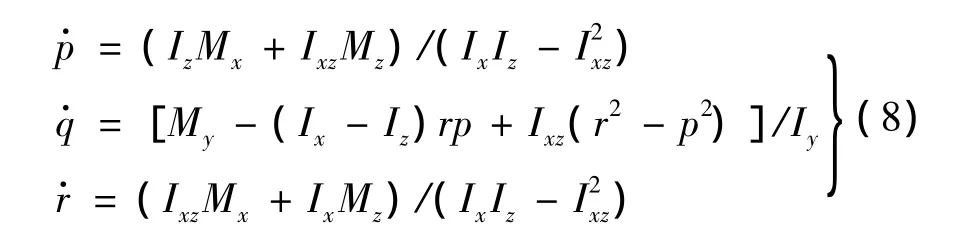
式中:T为发动机推力;D，C，L分别气动阻力、侧力与升力;I为转动惯量;Mfa为速度坐标系到机体坐标系的转移矩阵;Mx，My，Mz分别为机体系下三个方向的合外力矩。

1.3 数字仿真

以0°操纵角控制前轮，对滑跑动力学模型进行数字仿真，结果如图2所示。在仿真时间20 s内无人机空速达到起飞速度36.5 m/s，滑跑纵向位移415.4 m，侧偏距14 m(飞机侧偏是由于风洞试验得到的气动参数不对称导致)。

图2 无人机以0°操纵角滑跑结果Fig.2 Results of UAV running with zero control angle

从图2可以看出:无人机达到起飞速度时，三轮胎的支反力接近零值，但此时无人机仍不能起飞，需偏转襟翼到“起飞”位置，操纵升降舵面使无人机抬起前轮，继而操纵飞机离地。在跑偏过程中，由于机轮侧向力的不断增大，左右主轮支反力不再相等。飞机向右转弯，左主轮支反力大于右主轮支反力，这与实际相吻合。

2 地面操纵转弯数学建模

2.1 机轮模型

地面滑跑过程中，飞机的平面运动可简化为平动及转动两种运动的合成，其转动的速度瞬心变化由轮胎偏角引起，因此机轮状态分析对转弯特性求解十分关键。图3(a)为无人机主起落架机轮，通过侧偏特性实验可测得该机轮侧偏刚度等参数。图3(b)为机轮的力学特性示意图，可以看出滑跑中机轮状态复杂，受到侧向力、牵引力的同时还受到回正力矩作用。为简化计算，本文着重考虑侧偏角的影响。在运动特性上，侧偏角表示为轮胎速度相对机轮方向的偏角。

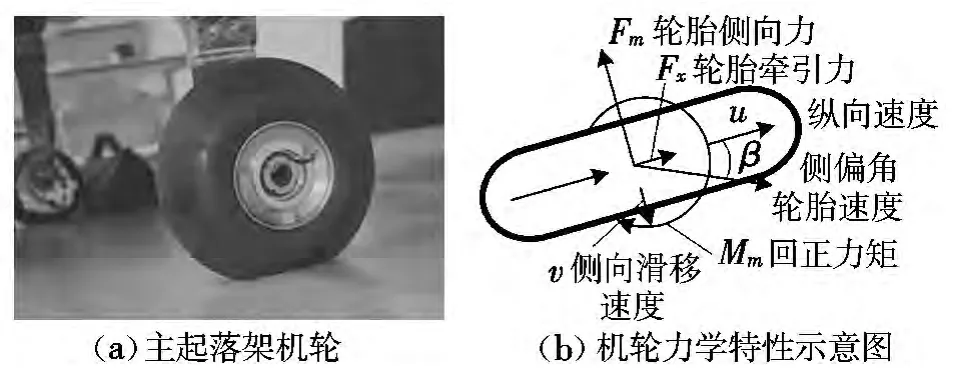
图3 无人机机轮及其力学特性Fig.3 The wheel of UAV and its mechanics schematic

图4 (a)为机轮的实际侧偏角示意图。图中:D，B，C分别为三轮胎的触地中心;P为前轮对中时的停机位置;AO为前轮旋转中心到重心O的距离(AO=an+t，OG=am);t为稳定距;DH为前轮触地中心的速度方向;GI为两主轮中点的速度方向。

由于无人机前起落架为摇臂式，旋转中心A不在前轮停机中立位置，考虑∠DOP很小，可近似认为DO=PO，从而将前轮触地中心放置在机体中心轴线上，如图4(b)所示。

图4 轮胎侧偏角示意图Fig.4 Slip angle of wheels

根据点的相对运动，轮胎触地中心速度可由机体质心速度与轮胎相对质心转动速度合成:

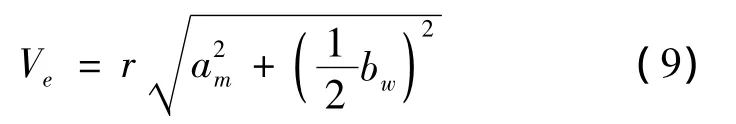
由图4(b)的几何关系可得:

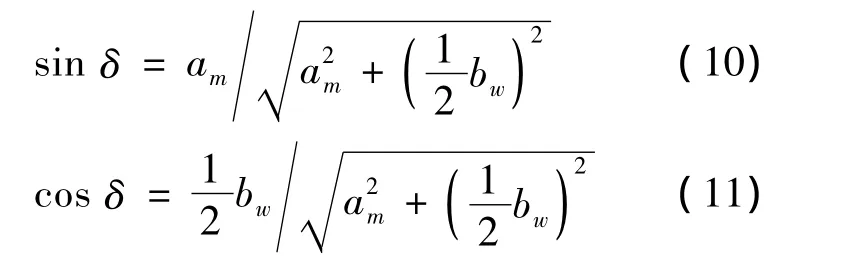
解得机体坐标系下的速度为:

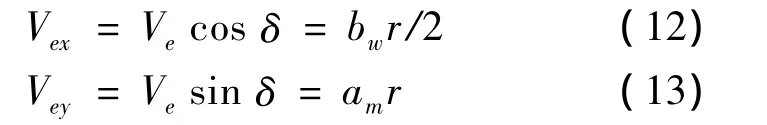
从而求得主轮及中心点的侧偏角为:

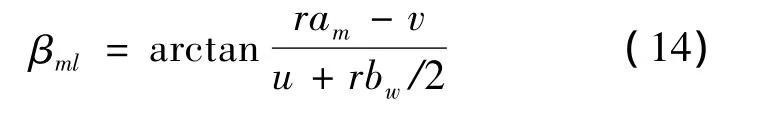
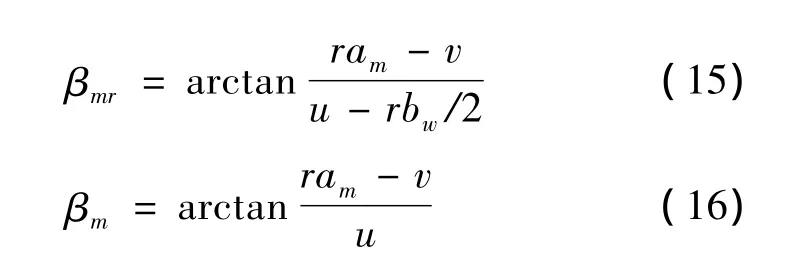
对于前轮，机轮可以相对机体旋转，因此前轮的侧偏角 βn=θl－θn，由运动学关系可得:

2.2 转弯半径计算方法

由于βm很小，文献［10］在计算飞机转弯半径时忽略了主轮的侧滑，但实际由于βm的存在会导致速度瞬心内移，使得转弯半径变小，加大了飞机的转弯离心力，更易导致飞机翻倒。因此从严酷性考虑出发，本文在计算转弯半径时加入了侧偏角的影响。

图5为飞机转弯半径计算示意图，其计算公式为:

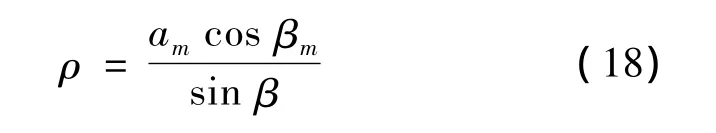
其中:

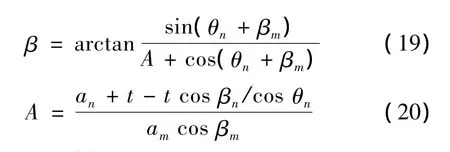
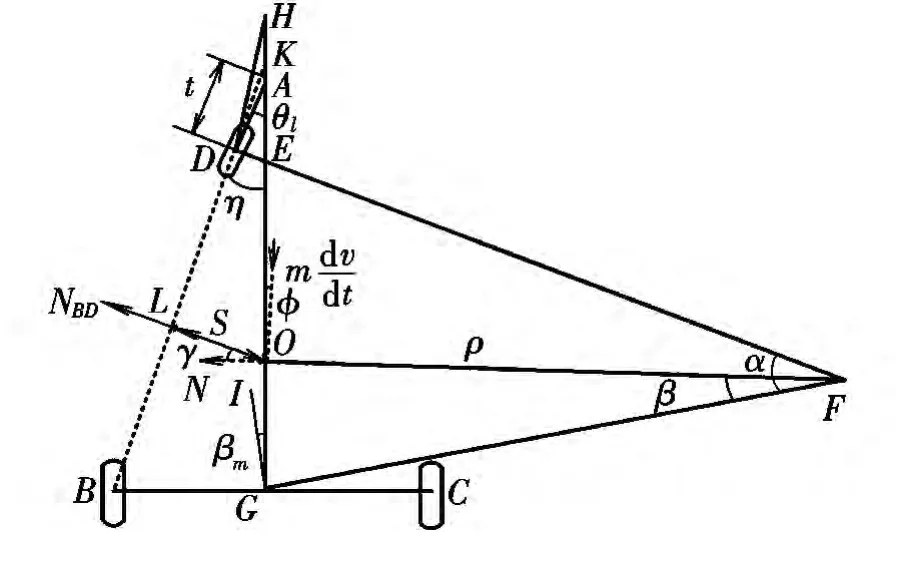
图5 飞机转弯半径计算示意图Fig.5 Turning radius of UAV

2.3 前轮极限操纵角计算方法

假设轮胎与地面的摩擦力足够大，未发生侧滑，则在翻倒力矩的作用下，飞机可能相对前轮及一侧主轮地面触点的连线BD翻倒。飞机的翻倒力矩为:

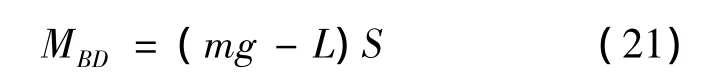
式中:L为升力;S为翻倒力臂。

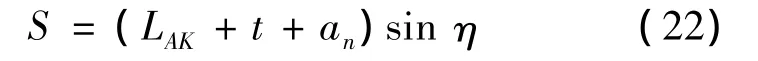
其中:

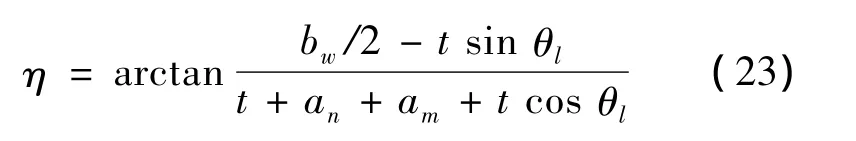
式中:LAK为AK间距离。

当飞机发生翻倒时，则有NBDh＞MBD(NBD为翻倒力，该力与前轮操纵角与转弯速度有关)。当飞机处于临界翻倒时:

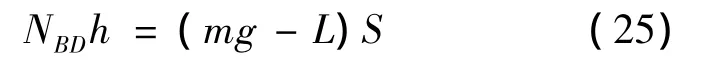
文献［10］将NBD定义为地面作用在轮胎上的所有摩擦力的合力(取反向)对BD轴垂线的投影，但摩擦力的计算涉及到摩擦参数及各轮胎状态的求解，结果不甚准确。根据达朗贝尔原理，作用在轮胎上所有摩擦力的合力与作用在飞机重心上的所有外力和惯性力的合力大小相等，方向相反。因此计算时，只需考虑作用在飞机重心上的所有外力和惯性力即可。

式中:N为转弯离心力，N=mV2/ρ;d v/d t为飞机的切向加速度。

由图5的几何关系可得:

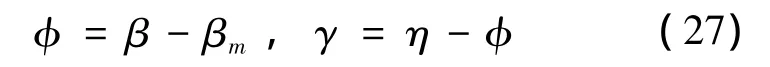
由式(27)可求得前轮极限操纵角θl与滑跑速度V的函数关系为:

可以看出，在各滑跑速度下的极限操纵角与无人机的受力状态、机轮状态及加速度有关，上述参数需联合动力学模型求解。

3 操纵转弯特性数值计算

联合动力学模型与转弯模型对转弯特性进行求解，流程图如图6所示。

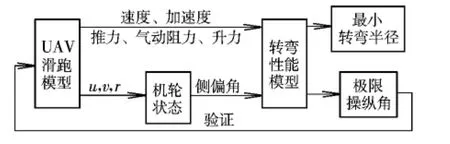
图6 转弯性能计算流程图Fig.6 Flow chart of turning capability

图7 为计算所得的转弯性能。可以看出，无人机地面操纵转弯时，极限操纵角随滑跑速度的增大而减小，最小转弯半径随滑跑速度的增大而增大。在高速阶段，必须对前轮施加控制约束，此时前轮转向作用不大，必须联合方向舵控制纠偏，此时操纵飞机极为危险，容易导致飞机侧翻事故发生。

图7 无人机转弯性能Fig.7 Turning capability of UAV

将所得的极限操纵角返还到无人机滑跑模型，由图2(a)得无人机在8.8 s时速度达到了20 m/s，由图7得此时的极限操纵角为1.88°。因此对该时刻的前轮操纵角输入幅值为1.88°的阶跃信号，持续时间2.5 s，仿真结果见图8，可以看出输入前轮操纵信号，三轮胎的侧向力瞬间增大，撤销信号后又迅速减小。由于侧向力的影响，左右主轮支反力不再相等，飞机右拐弯过程中右轮支反力逐渐变小，到11.3 s时接近为零，此时飞机处于临界翻倒状态。

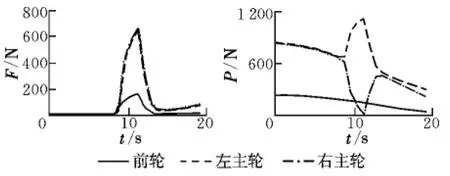
图8 转弯模型验证Fig.8 Tuning model verification

然而转弯模型是在假设飞机不处于侧滑，侧向力恒定由侧偏角与侧偏系数乘积得到的情况下建立的，而实际情况转弯的向心力由轮胎的侧向力提供。当转弯速度或者转弯角过大，轮胎侧向力超出轮胎与地面间的侧向摩擦力，飞机就会出现侧滑现象。由图8可知，在临界翻倒时侧向力最大达到了664.5 N，极有可能超出运动机轮的极限摩擦力，因此有必要通过实验验证无人机在翻倒前是否已经发生了侧滑。

4 结束语

本文根据某型无人机结构参数和气动特性研究了飞机的地面运动品质与转弯性能，建立了无人机地面滑跑动力学模型，求解了无人机的瞬态参数。针对无人机发生的侧滑和侧翻问题，建立了地面操纵转弯数学模型，计算了无人机在各滑跑速度下所允许的极限操纵角和最小转弯半径。结果表明前轮操纵角在存在7°机械限位的情况下，与滑跑速度仍需有定量的约束关系。本文方法明确了无人机的转弯性能，保证了无人机的安全起降，可以为滑跑自主纠偏技术打下基础。

［1］ Pollack H M，Urch R E.Landing gear design requirements for bomb-damaged runway operations［R］.SAE-91199，1991.

［2］ Khapane P D.Simulation of asymmetric landing and typical ground maneuvers for large transport aircraft［J］.Aerospace Science and Technology，2003(7):611-619.

［3］ 董健康，王洁宁，王安国，等.飞机推出和跑道掉头滑行行为计算方法［J］.航空学报，2012，33(12):2183-2191.

［4］ Khapane P D.Gear walk instability studies using flexible multibody dynamics simulation methods in SIMPACK［J］.Aerospace Science and Technology，2006(10):19-25.

［5］ 顾宏斌.飞机地面运行的动力学模型［J］.航空学报，2001，22(2):163-167.

［6］ 钱小妹.飞机操纵前轮转弯特性仿真研究［D］.南京:南京航空航天大学，2008.

［7］ 张明，聂宏，魏小辉.多轮起落架飞机滑行操纵动力学分析［J］.南京航空航天大学学报，2008，40(4):542-546.

［8］ 朱天文.飞机地面操纵转弯半径和转弯速度计算方法研究［J］.飞机设计，2003，24(3):31-34.

［9］ 肖业伦.航空航天器运动的建模［M］.北京:北京航空航天大学出版社，2003.

［10］高泽迥.飞机设计手册(第14分册):起飞着陆系统设计［M］.北京:航空工业出版社，2002.