地面效应下飞机空投阵风减缓LQR控制

2015-12-28陶国文孙秀霞刘树光梁帅付强

飞行力学 2015年4期

陶国文，孙秀霞，刘树光，梁帅，付强

(空军工程大学航空航天工程学院，陕西西安710038)

0 引言

运输机超低空空投主要用于重型装备的精确投放，是空投领域的一个重点和难点，围绕超低空空投的研究具有重要的军事意义和应用价值［1］。

当飞机近地飞行时，升力增大，阻力减小，升阻比急剧升高，称为地面效应［2］。地面效应一般能提高飞机的气动效率，但往往也给飞机纵向稳定性带来不利影响。近地飞行时，地效飞机的气动力不仅与迎角有关，而且与飞行高度有关，因而影响其纵向稳定性的因素相对复杂［3］。

在空投过程中主要采用分离法进行建模，以便于对各种外界干扰作处理分析［4］。在建模的基础上采用最优控制方法，简单而且易于在工程中实现，也取得了良好的控制效果［5］。但对于在地面效应影响下的研究，主要集中在空投模型的改进上以及控制方法的设计［6］。本文在此方向上的研究对于后期的控制律设计以及相关地面实验具有重要的借鉴意义。

阵风对飞机的效应主要是通过改变流场从而导致飞机表面尤其是机翼压力分布的变化，从而产生附加的气动力。国内外许多文献对基于阵风干扰的运输机空投进行了研究，主要集中在基本模型上加入阵风干扰，但在超低空空投中，地面效应的影响往往不可忽略。本文在基本模型的情况下，在考虑地面效应的基础上，对空投模型作了改进，在阵风干扰的影响下，进行了LQR控制律设计及其参数遗传算法优化。

1 地面效应下空投建模

1.1 地面效应影响分析

超低空飞行时，地面效应对飞机纵向气动力及力矩的影响主要由以下三部分组成:自由涡引起的升力系数变化、附着涡引起的升力系数变化和平尾的升力与下洗角变化［7］。

以某大型运输机为例，未开启襟翼情况时，本文通过在一般空投模型的基础上，在不同空投高度情况下，主要进行了飞机纵向升力和俯仰特性的仿真，得到了地面效应影响下的纵向气动力及力矩随高度的变化规律，如图1所示。

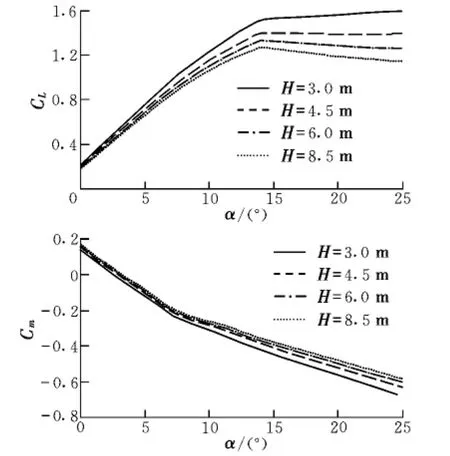
图1 地面效应影响下气动系数的变化Fig.1 Variation of ground effect vs aerodynamic coefficient

综上所述，地面效应影响下，载机纵向气动导数变化规律如下:(1)随着高度的降低，飞机的升力系数CL逐渐增大;(2)由于机翼升力增加、下洗减小及平尾升力的增加，导致低头力矩增大，即俯仰静稳定性增强。因此，当飞行器超低空飞行时，由于地面效应的影响，CL和Cm对H的气动导数CLH和CmH不能忽略，故传统小扰动基准运动的基本假设“不考虑飞行高度微小变化对气动力的影响”将不成立。

由于受到地面效应的影响，使飞机纵向运动气动导数中增加了CLH和CmH，横航向气动导数中增加了 Clφ和 Cnφ，因此，纵向、横航向运动参数对基准运动(V0，α0，δe0)的泰勒级数一阶展开与传统的线性化形式不同，小扰动运动方程也不同。

1.2 纵向小扰动方程的建立

从地面效应影响下的飞机运动参数泰勒级数展开出发，建立了不同于传统自由气流环境的飞行小扰动运动方程。

地面效应影响下，升力L、阻力D、侧力C、俯仰力矩M、滚转力矩 K、偏航力矩 N，对基准运动的Taylor级数一阶展开如下式所示。

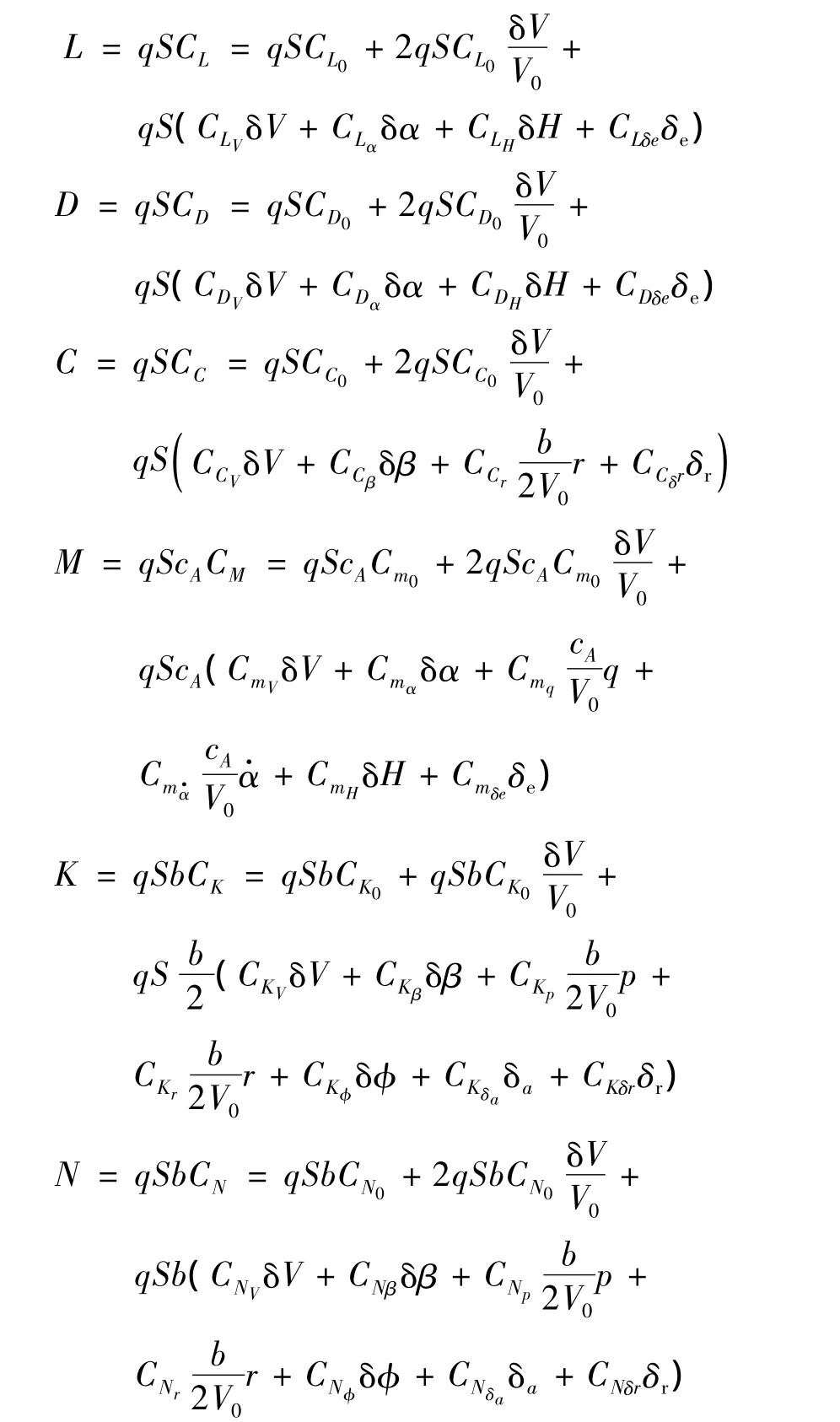
式中:V0为基准运动配平速度;CD0为零升阻力系数;Cm0为零升力矩系数;(CLα，CDα，Cmα)为迎角引起的升力、阻力与俯仰力矩系数;(CLδe，CDδe，Cmδe)为升降舵引起的升力、阻力与俯仰力矩系数。由于飞机存在Oxbzb对称平面，所以横航向零力矩系数CC0=CN0=CK0=0。

飞行器六自由度全量运动方程如下:

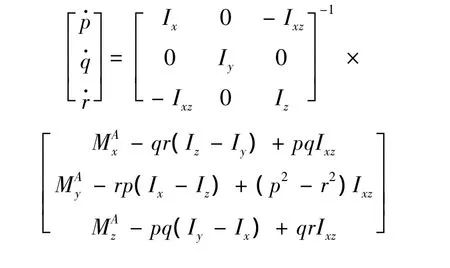
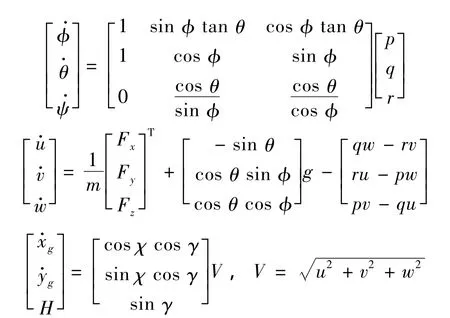
本文只考虑阵风对运输机空投过程中纵向通道的影响，在文献［8］的基础上可知，某型运输机在特定状态下纵向通道的状态空间模型为:

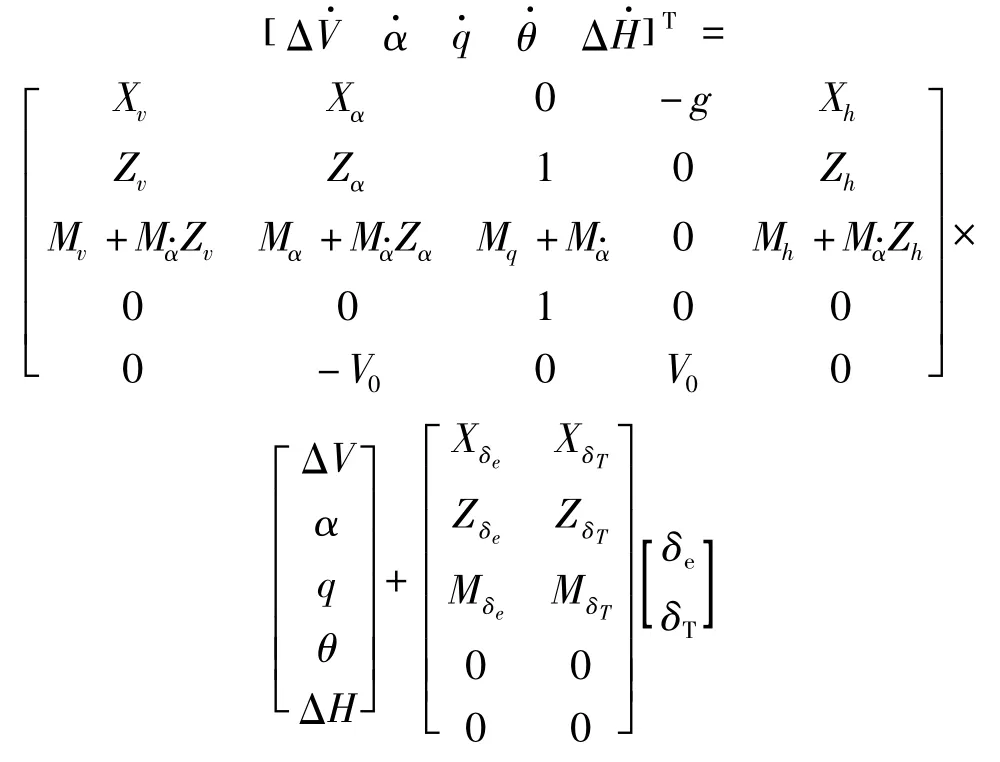
2 阵风对飞机运动的影响

2.1 阵风模型

阵风载荷减缓系统(Gust Load Alleviation，GLA)是随控布局飞机的一项功能。假设阵风及测量噪声为符合正态分布的平稳随机过程，那么状态响应和输出以及控制律也是同一类型的随机控制，对于这类控制问题，线性二次型最优控制(LQR)理论已经得到了具体应用。

水平前向风相对于飞行速度是较小量，因此阵风载荷减缓系统在纵向只考虑垂直紊流风的影响。取垂直紊流风的一维Dryden谱，其功率谱密度为:

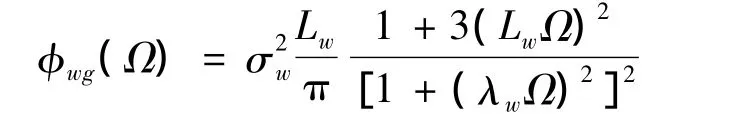
由于Dryden谱为有理谱，所以根据有理谱成形理论，可以认为紊流风是由单位强度白噪声作为输入的一个线性滤波器的输出，由此可以得到垂直紊流风的线性化模型［9］:

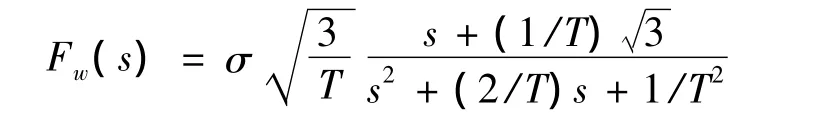
式中:T为风干扰的特征长度与航迹速度的比值。

2.2 飞机的阵风纵向模型

由紊流扰动在纵向通道中对飞行的影响可知，阵风在纵向引起了迎角增量Δαw。因此结合飞机地面效应下纵向小扰动方程与紊流扰动的线性化模型，建立了飞机的阵风数学模型。因为阵风引起的迎角变化Δαw不是状态量也不是可控量，所以改写为如下形式:

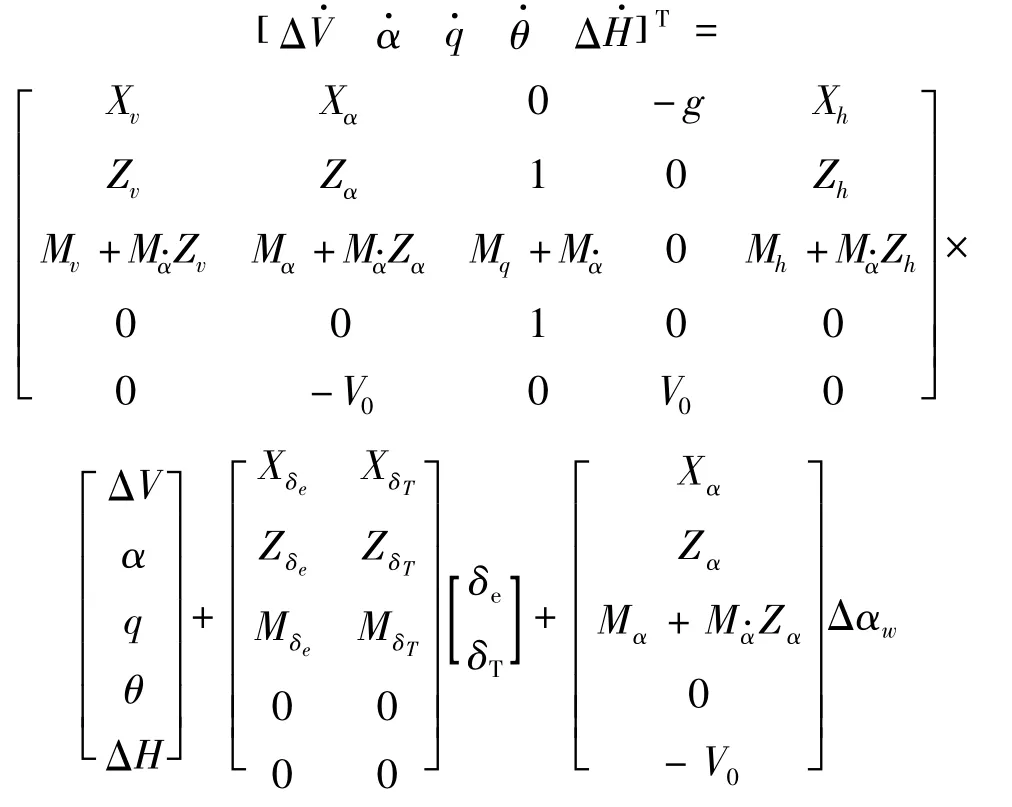
上式即为本文中要讨论的飞机的阵风模型。由飞控理论可知，阵风引起的迎角变化量Δαw与阵风风速Vw、空速Va之间的关系为:

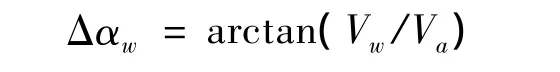
2.3 Simulink模型的建立

以某型运输机最大载重飞行为例，飞行高度为10 m，相对空速为80 m/s，襟翼开度为50%，根据上一节建立的飞机的阵风模型，原系统仿真模型整体结构如图2所示。

图2 仿真模型整体结构图Fig.2 Overall structure of simulation model

由Simulink中对未加控制条件下的仿真可以看出，由于阵风和地面效应的影响，原系统的过载呈发散状态，俯仰角速率变化量稳态误差过大，系统的稳定性能不足，效果很差。俯仰角和迎角也随着空投时间的增大而增大，从而可能导致空投载机的不稳定。

3 LQR控制律设计

3.1 LQR控制律设计思路

根据已知的权值矩阵Q和R，Matlab提供函数K=LQR(A，B，Q，R)来解算［10-11］。

3.2 超低空空投LQR控制器设计

LQR控制下的仿真模型结构如图3所示。

图3 LQR模型结构图Fig.3 LQR model structure

根据经验取性能指标中的矩阵Q，R为:

解得反馈增益矩阵为:

将K带入图3的模型中运行后，得到5个输出状态的输出曲线。由输出仿真图可知，加入LQR控制器后的系统输出过载和俯仰角速率、迎角和俯仰角经过较短的时间都达到稳定状态，但是稳态误差依然存在且误差值较大。

3.3 矩阵Q和R的遗传算法寻优

遗传算法按所选择的适配值函数并通过遗传中的复制、交叉及变异对个体进行筛选，使适配值高的个体保留下来，组成新的群体，新的个体继承并优于上一代的信息。遗传算法的算法简单，可并行处理，并能得到全局最优解。

在本文中，设置适配度函数为5条输出曲线稳态误差之和，通过迭代仿真求得使其最小的Q，R中的权值，获得最优效果。

由遗传算法优化图可以得出矩阵Q，R的最优解为:

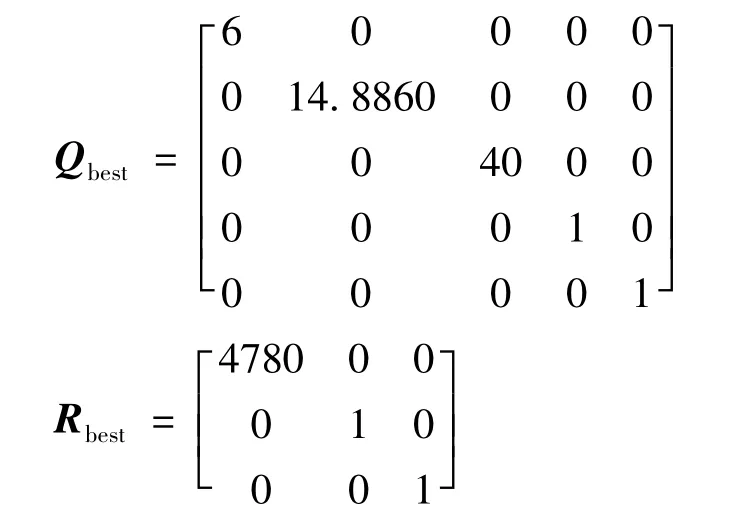
解得优化后的反馈增益矩阵为:

4 仿真结果及分析

将K矩阵带入图3的模型中运行后，得到各输出状态曲线如图4所示。

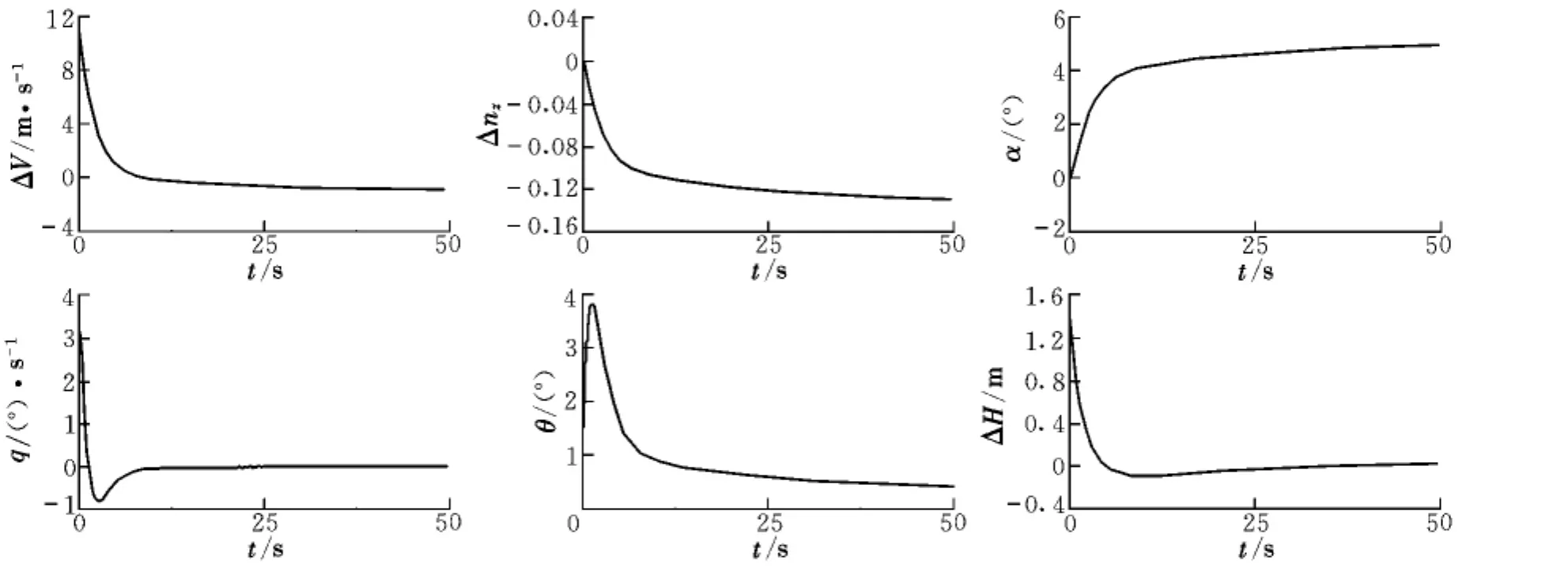
图4 遗传算法求得的LQR控制器飞机纵向仿真结果Fig.4 LQR controller aircraft longitudinal simulation results obtained by genetic algorithm

由图4可以看出，在初始阵风扰动加入的时刻，速度有一个15%左右的突变，纵向通道高度H也有一个12%左右的变化，相应的迎角、俯仰角和法向过载都有一个突变，在5 s以后飞机逐渐趋于稳定，速度和高度变化也趋于零，表明该纵向系统的过载和俯仰角速率的变化已经非常微弱，最终6个输出曲线都达到了满意的控制效果。因此可以得出，在超低空空投基本模型的基础上引入地面效应的影响，经过对模型的改进使之更加符合工程实际，而且遗传算法优化的LQR控制器使原系统具有了良好的稳态性能，改善了运输机超低空空投过程的稳定性和操纵性能。