基于Johnson－Cook本构模型的弹带挤进过程数值模拟

王 鹏，杨国来，葛建立，孙全兆，梁传建

（南京理工大学 机械工程学院，南京210094）

对于火炮的内弹道而言，弹带挤进是一个很重要的过程。该过程直接改变膛内容积的变化规律，对膛内火药气体生成速率、膛内压力的变化、火炮初速的大小产生重要影响，而且与身管寿命、射击密集度以及射击安全性等火炮武器关键性能指标密切相关［1］。然而，传统内弹道理论一般忽略挤进过程，认为该过程瞬间完成。弹丸挤进过程实际是弹带和身管内膛发生接触碰撞，膛线逐渐侵彻弹带，弹带材料不断失效和破坏的过程，具有高瞬时、强冲击、高温变、高速变的特点，挤进阻力和变形的规律十分复杂［2－3］。由于具有诸多难点，目前现有的研究理论与实际挤进过程仍有较大差距，亟需针对挤进过程展开研究工作。

本文以某大口径火炮弹带挤进过程为研究对象，开展其非线性动力学建模与数值计算研究，提出运用Johnson－Cook本构关系模型描述材料变形和失效问题，建立精确的弹带挤进过程模型，重点针对该大口径火炮发射条件下弹带挤进过程的弹带大变形问题、弹丸运动规律、挤进压力、挤进阻力变化规律进行数值计算研究，并分析摩擦性质对挤进过程的影响。

1 Johnson－Cook本构关系模型

材料本构关系是材料变化的体现与描述，本构关系体现了材料在外界作用下发生变形，强度随着应变及温度等因素改变的情况，在有限元建模仿真中具有重要的地位。

在大口径火炮射击时，弹丸挤进膛线的过程是一个复杂的材料塑性流动过程。本文研究的弹带材料为紫铜，弹带在挤进过程中经历弹塑性大变形及损伤，最终发生韧性断裂，涉及到弹带材料的应变硬化、应变率硬化和温度软化，可采用Johnson－Cook塑性及断裂失效模型［4－5］。

Johnson－Cook本构关系模型（简称J－C模型）是一个经验性的粘塑性模型，是由Johnson和Cook于1983年提出的用于高应变率和高温情况下的本构关系模型［4］，形式简单，使用方便，在冲击动力学中得到了广泛应用。该模型由两部分组成。

第一部分为应力－应变关系，表示为

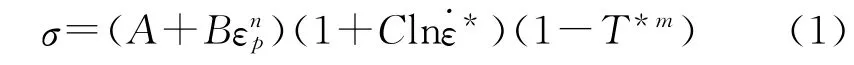
式中：σ为von Mises屈服应力；A为准静态实验下的屈服强度；B，n为应变强化参数；C为经验性应变率敏感系数；m为温度软化指数；εp为等效塑性应变为无量纲的等效塑性应变率。相对温度：

式中：Tr为参考温度（一般取为室温），Tm为常态下材料的熔化温度。

第二部分为断裂时的应变：

式中：应力三轴度σ＊＝p／σeff，p为静水应力，σeff为等效应力；d1，d2，d3，d4，d5分别为材料参数，由试验测试确定。

材料的失效由塑性应变累积准则来判断：

挤进过程涉及的紫铜、炮钢材料参数见表1，表中ρ、E、ν分别为密度、弹性模量与泊松比。

表1 挤进系统主要材料力学性能

确定弹带材料紫铜的Johnson－Cook模型参数，对于准确模拟挤进过程非常重要。紫铜是广泛使用的传统工业材料，可在参考文献［4－5］中引用现成的本构模型参数，由表2列出。

表2 紫铜材料Johnson－Cook本构关系参数

2 挤进模型的建立

2.1 挤进过程建模基本假设

弹丸挤进过程的受力和变形情况非常复杂，具有高瞬时、强冲击、大变形、高速变的特点。为了提高所建模型的仿真效果，忽略次要的影响因素，对弹带挤进内膛过程作如下基本假设［6］：

①由于挤进过程非常短暂，故假定挤进过程是在室温情况下的绝热冲击过程；

②卡膛到位后，认为弹带和坡膛倾角紧密配合，并将此位置作为弹丸挤进过程的开始；

③忽略不均衡问题，假定弹丸与身管轴线共心，摩擦力与运动阻力都沿轴线方向；

④忽略弹丸前部的空气阻力和激波的影响；

⑤忽略弹带的初始应力及有关温度等影响；

⑥不考虑身管的后坐运动。

2.2 挤进系统的网格划分

在挤进系统的模型网格划分中，对于重点考察研究的弹带等部位，尽量将网格精细化处理，并采用ALE自适应网格技术，选择C3D8R（8节点减缩积分单元）作为划分的网格单元类型。为减少计算时间，对于弹体、膛线和身管等部位，用分割网格的方法以减小总体网格模型的规模。图1、图2为建立的网格模型。

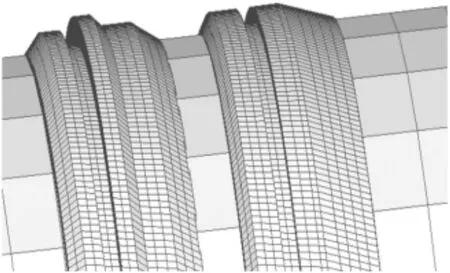
图1 弹带和弹丸网格划分

图2 膛线和身管网格划分

各部分网格数量见表3所示。

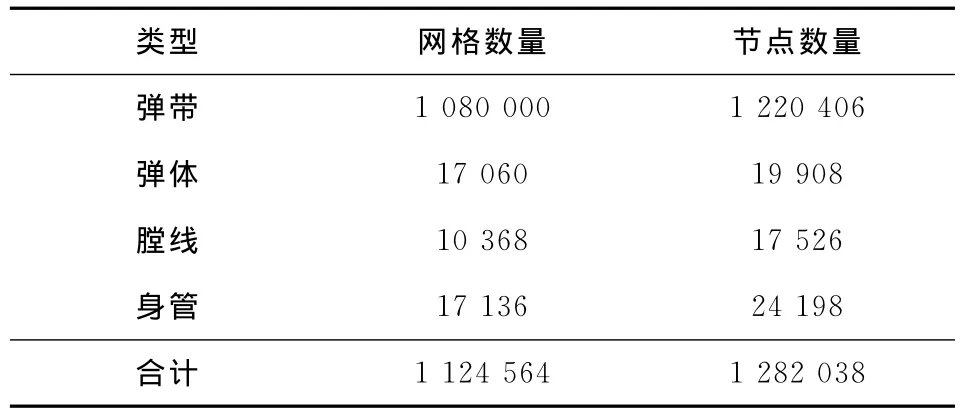
表3 各部分网格与节点数量

2.3 载荷和边界条件

弹底压力是弹丸所受到的最主要作用力，是推动弹丸向前运动的动力。通过实弹射击测试得到该大口径火炮最大号装药条件下挤进时期膛底压力变化曲线，由文献［1］所述内弹道计算中应用的压力换算关系式（5），换算得到弹底压力，如图3所示。

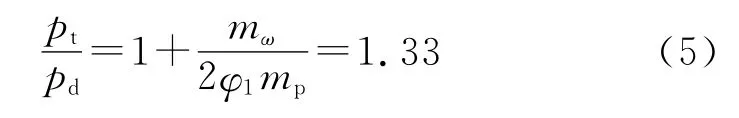
式中：pd为弹底压力；pt为膛底压力；mp为弹丸质量；mω为发射药质量；φ1为次要功系数。

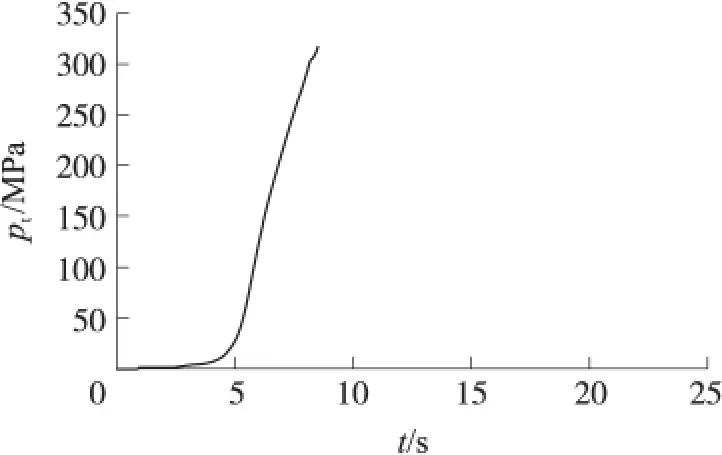
图3 膛内压力曲线数据

将转换得到的弹底压力作为弹底载荷条件。边界条件对弹体没有任何约束，对身管作全约束。

3 数值仿真计算及结果分析

将建立好的挤进系统模型提交ABAQUS运算，得到挤进数值模拟结果，重点针对弹丸挤进过程中弹带变形和刻痕的形成过程、挤进过程弹丸运动规律、弹带动态挤进阻力、挤进压力进行分析。

3.1 弹带变形及刻槽形成过程

弹带槽的形成过程是挤进过程研究中一个比较关心的问题。利用ABAQUS／Explicit进行数值计算，得到弹带挤进膛线的变化过程。按照挤进进程的时间先后，用明显变形后的网格图来显示弹带槽的形成过程，如图4所示。

图4（a）示意在t＝3.0ms时刻之前，弹带变形一直处于较低的水平，也就是说此时刻以前，弹带只发生了弹性变形，还没有出现材料的断裂破坏；图4（b）显示，t＝4.0ms时弹带网格的部分区域发生材料失效断裂，弹带已显现出变形刻槽；图4（c）显示t＝5.0ms时刻第一条弹带部分已经出现断裂刻槽，弹带已经被明显切削挤进；图4（d）显示了t＝6.0ms时刻第一条弹带即将切削完毕的情况；图4（e）显示t＝6.5ms时第二条弹带前部被挤压变形的情况；图4（f）显示t＝7.0ms时第二条弹带进一步被挤压的情况；图4（g）显示t＝7.5ms时第二条膛线整体即将被切削完毕的情况；图4（h）显示了t＝8.0ms时挤进完成后的弹带网格图，刻槽形成。

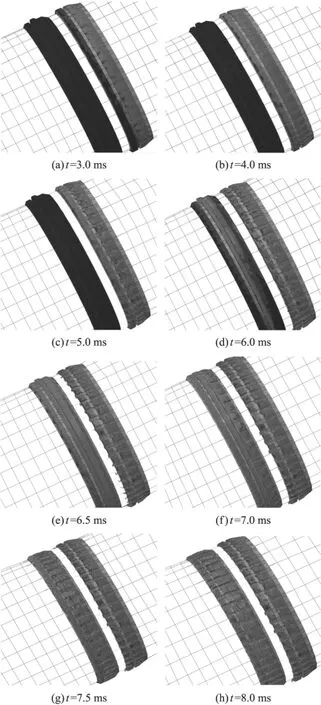
图4 挤进过程中不同时刻弹带网格变形图

通过以上弹带网格变形图，可以看出，弹带在挤进过程中不断发生材料失效，最终被切削成刻槽。通过与实弹射击回收得到的弹带外形（如图5所示）对比，数值模拟和实弹射击得到的弹带外形基本一致。

图5 射击后的切削弹带

3.2 弹丸运动规律

根据上文中关于挤进模型的基本假设，取模型中弹丸质心位置的节点，可得弹丸的运动变化规律。

如图6～图8所示，分别为挤进模型数值模拟计算得到的弹丸质心位移（s）－时间曲线、速度（v）－时间曲线和加速度（a）－时间曲线。

图6 弹丸质心运动位移－时间曲线

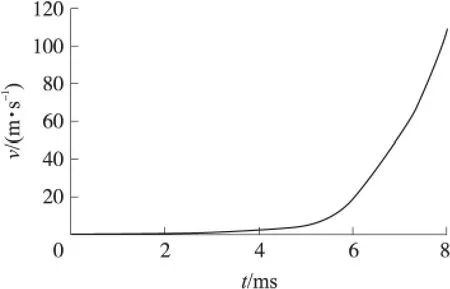
图7 弹丸质心运动速度－时间曲线

图8 弹丸质心加速度－时间曲线

分析图6可知：弹丸在2.92ms时刻前位移为0mm，将该时刻作为弹丸开始运动时间，即t1＝2.92ms。该时刻以后，弹丸开始移动；并且随着时间的增加，位移增长的速率不断增加。

分析图7可知：弹丸在2.92ms前速度基本为0；2.92ms时刻以后，弹丸速度开始增加，说明开始移动，并随着时间的增加，速度增长的速率不断增加。

分析图8可知：在前2.92ms时间内弹丸加速度基本为0；2.92ms时刻后弹丸开始逐渐出现加速度，并且随着弹底加速度上升而迅速上升；6.74ms时刻出现下降沿，原因是挤进阻力的增加速率超过了弹底压力的速率；随着压力的增加，7.02ms时刻后加速度重新呈现增长趋势。

3.3 弹带挤进阻力变化

本文提出一种实用的挤进阻力求解方法，针对弹丸膛内轴向受力情况，根据牛顿第二定律，可得到挤进过程运动方程：

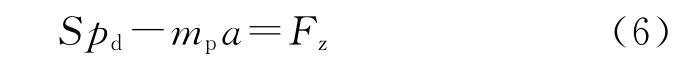
式中：Fz为挤进阻力，S为弹底面积，mp为弹丸质量；a为弹丸加速度。代入上文得到的加速度变化规律，即可得到弹带挤进阻力－时间曲线，如图9所示。

为清晰起见，图9给出挤进阻力明显增加阶段的挤进阻力－时间曲线。随着弹带变形程度增加，变形阻力逐渐增大；到7.14ms时刻挤进阻力达到最大值，对应的最大挤进阻力为1 420kN。达到最大值后，弹带变形量逐渐减小，挤进阻力逐渐降低，达到某值后保持稳定，说明已经挤进完成。

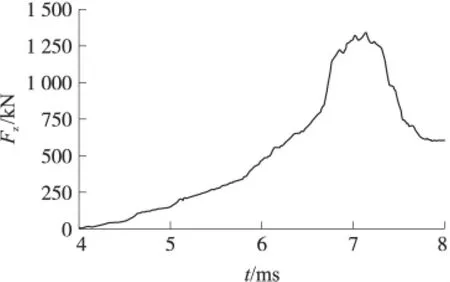
图9 挤进阻力－时间曲线

文献［7］描述了美国某155mm榴弹炮运动阻力曲线，如图10所示。该曲线中，位移40mm处出现最大挤进阻力为1 040kN，该结论与本文计算结果数量级相当并数值接近。

该火炮阻力曲线与本文得到的曲线变化规律相近，弹底压力增大到一定值后，弹丸才开始运动；弹带变形量不变时，挤进阻力也会保持稳定；弹丸挤进完成后阻力下降并保持在一定值。这些研究结论的吻合也佐证本文结论的正确性。

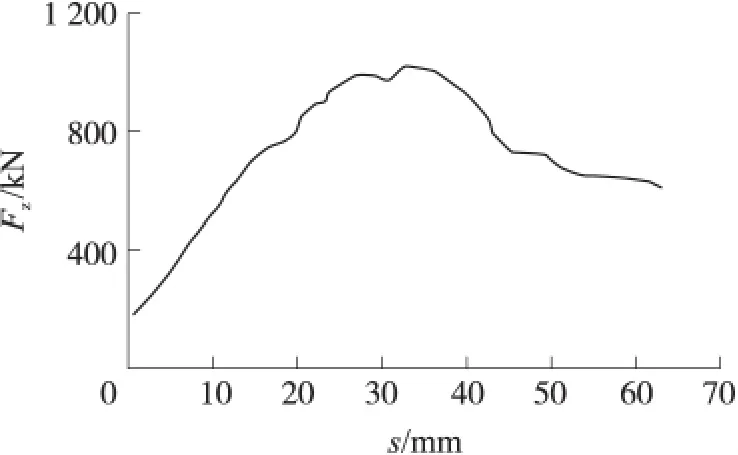
图10 美155mm榴弹炮弹带挤进阻力变化

3.4 启动压力与挤进压力

文献［8］中作了如下定义：启动压力是指弹丸开始运动瞬间对应的火药气体平均压力；挤进压力指在弹带全部挤进膛线瞬间与之相应的弹后火药气体燃气的平均压力。

由上节论述，弹丸开始运动时间t1＝2.92ms，该时间对应的火药气体平均压力为11.4MPa，即弹丸启动压力为11.4MPa。

对于该大口径火炮，弹带完全挤进膛线需要的行程为98mm。由弹丸位移－时间曲线，位移为98mm对应的时刻为7.68ms，该时刻对应的火药气体平均压力为243.9MPa，即挤进压力为243.9MPa。

对应的弹丸速度为98.2m／s，该大口径火炮初速为1 050m／s，即挤进完成时弹丸速度已经达初速的9.4%。内弹道过程中最大膛压为374.6MPa，挤进压力为最大膛压的65.16%。

将计算得到的结果归纳，得表4，表中t、p′、s、v分别为时间、膛内火药燃气压力、弹丸行程与弹丸速度。

对从弹丸启动瞬间时刻t1至挤进阻力达最大时刻t2的火药气体压力积分，并求取平均值：

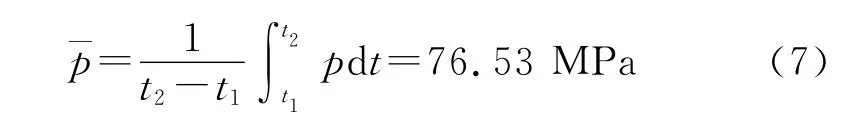
式中：p为膛内火药燃气平均压力。

这与传统内弹道计算初始条件通常取为30MPa是有明显差异的。

以上这些结论与前人的一些研究结论是相当吻合的。文献［9］的研究发现：挤进终了时的燃气压力远大于瞬时挤进所采用的30MPa，挤进完成时的挤进压力为最大膛压的65%；挤进过程所需要的时间为火药全部燃烧完时间的25%～33%，且挤进瞬间已经燃烧去火药的10%～15%；挤进完成瞬时弹丸速度已达初速的10%。文献［10］通过测试得到射击条件下采用铜弹带的海30炮挤进压力为209MPa，计算值为201.3MPa，本文计算结果与之在数量级上也相当。

这些文献结论可以从一些方面佐证本文数值模拟结果的合理性，但若要精确的验证，需要对该大口径火炮进行试验测试，这些将在下一步工作中进行。

4 摩擦性质对挤进过程的影响

弹带内膛之间的摩擦阻力与弹带塑性变形阻力是弹带挤进阻力的2个重要组成部分。当弹丸开始运动后，弹带与坡膛、膛线开始接触碰撞变形，这个过程中所引起的正压力是很大的。而摩擦阻力的大小取决于正压力和摩擦系数，故在正压力很大的情况下，摩擦系数对挤进阻力的影响是显著的。

4.1 不同摩擦性质下挤进变化

为了研究弹丸在不同摩擦性质下的挤进变化规律，分别建立了某大口径火炮在摩擦阻力系数μ分别为0，0.05，0.1，0.15 4种不同摩擦性质下的挤进模型，并分别计算出不同摩擦性质下的挤进过程变化，表5列出了不同摩擦性质下的挤进过程计算结果，表中t0、Fzm、p0分别为挤进完成时刻、最大挤进阻力与挤进压力。

表5 不同摩擦性质下挤进过程变化

可以看出，摩擦阻力变大，挤进时间越长，挤进阻力越大，对应的挤进压力也就越大。相反，摩擦阻力变小，挤进就越容易，时间越短，相应的挤进压力也会降低。

4.2 “首发近弹”原因的简单讨论

现役火炮在实弹射击时，往往会出现“首发近弹”现象，即第一发射弹的实际射程要比预定的射程近一定距离。

本文尝试从挤进的角度去分析首发近弹产生的原因。经验表明，火炮在每天第1发射击时出现首发近弹的现象。通过对同一天各发的射击过程和射击条件进行跟踪，发现一个明显特征是每天首发射击时炮膛内有油，其后的各发膛内没有油。正常情况下，紫铜弹带与炮钢间的摩擦系数一般取为0.19左右，火炮在实弹射击前，都要进行正常的维护与保养，擦拭炮膛，涂抹炮油，会将摩擦系数降低到0.05以下。首发射击后，高速、高温、高压的膛内火药气体会把膛内表面的涂油燃烧掉，而后进行射击的各发是内膛表面无油条件下的弹带挤进过程，弹丸的运动压力、弹道性能也均恢复到正常状态，不会再发生近弹的现象。

表6为首发射击与第2发射击挤进变化对比。首发炮弹由于油膜层的作用，初始摩擦系数为0.04，计算后得到挤进完成时刻为7.20ms，对应的挤进压力为212.9MPa；第2发弹初始摩擦系数恢复到0.19，计算得到挤进完成时刻为7.47ms，对应的挤进压力为275.4MPa。

表6 首发射击与第2发射击挤进变化对比

同时，首发弹比第2发弹的启动压力要小，即弹丸在较低的压力下就开始运动，这会明显地影响到点传火和火药燃烧过程，使最大膛压变低，弹丸初速变小，从而导致“首发近弹”现象发生。

5 结束语

本文以某大口径火炮弹带挤进过程为研究对象，采用Johnson－Cook本构模型描述了材料的破坏失效，结合实验测试数据在有限元软件ABAQUS中建立了挤进过程的非线性动力学模型，利用显式数值积分算法对弹带挤进过程的非线性动力学进行了数值模拟。重点针对该大口径火炮发射条件下弹带挤进过程的弹带刻槽形成过程、弹丸挤进运动规律、挤进阻力动态变化、挤进压力进行了研究，并探讨了摩擦性质对弹带挤进过程的影响，主要得到了以下结论：

①采用Johnson－Cook本构模型，较好地描述了弹带材料不断变形、断裂失效，得到了弹带刻槽形成过程。

②通过数值计算得到了弹丸挤进运动规律、挤进阻力动态变化规律，以及确定了启动压力与挤进压力，并论证了结果的可信性。

③得到了摩擦阻力对挤进过程的影响，摩擦系数越大，挤进时间越长，挤进阻力越大，对应的挤进压力也就越高；并从这一角度对“首发近弹”现象做出了解释。

［1］钱林方.火炮弹道学［M］.北京：北京理工大学出版社，2009：145－147.QIAN Lin－fang.Ballistics of guns［M］.Beijing：Beijing Institute of Technology Press，2009：145－147.（in Chinese）

［2］樊黎霞，何湘玥.弹丸挤进过程的有限元模拟与分析［J］.兵工学报，2011，32（8）：963－969.FAN Li－xia，HE Xiang－yue.Finite element simulation and process analysis of projectile entering into barrel［J］.Acta Armamentarii，2011，32（8）：963－969.（in Chinese）

［3］陆野，周克栋，赫雷，等.某大口径枪械内弹道挤进时期的数值仿真与分析［J］.弹道学报，2014，26（2）：67－71.LU Ye，ZHOU Ke－dong，HE Lei，et al.Numerical simulation and analysis of engraving duration during interior ballistics of some large－caliber small arms［J］.Journal of Ballistics，2014，26（2）：67－71.（in Chinese）

［4］JOHNSON G R，COOK W H.A constitutive model and data for metals subjected to large strains，high strain rates and high temperatures［C］／／Proceedings of the 7th International Symposium on Ballistics.Hague：IBC，1983：541－547.

［5］JOHNSON G R，COOK W H.Fracture characteristics of three metals subjected to various strains，strain rates，temperatures and pressures［J］.Engineering Fracture Mechanics，1985（21）：31－48.

［6］张振辉.末制导炮弹与火炮身管相互耦合机理及适配性技术［D］.南京：南京理工大学，2013：47－51.ZHANG Zhen－hui.Suitability technology and inter－coupling mechanism of guided projectile entering into barrel［D］.Nanjing：Nanjing University of Science and Technology，2013：47－51.（in Chinese）

［7］张喜发，卢兴华.火炮烧蚀内弹道学［M］.北京：国防工业出版社，2001：44－45.ZHANG Xi－fa，LU Xing－hua.Interior ballistics of erosion guns［M］.Beijing：National Defense Industry Press，2001：44－45.（in Chinese）

［8］金志明.枪炮内弹道学［M］.北京：北京理工大学出版社，2011：57－58.JIN Zhi－ming.Interior ballistics of guns［M］.Beijing：National Defense Industry Press，2011：57－58.（in Chinese）

［9］丘尔巴诺夫E B.挤进时期内弹道学与挤进压力计算［M］.杨敬荣，译.北京：国防工业出版社，1997：8－20.

［10］何勇.挤进过程实验研究［J］.弹道学报，1996，8（4）：33－36.HE Yong.Experimental research of engraving process［J］.Journal of Ballistics，1996，8（4）：33－36.（in Chinese）