中心药爆炸抛撒金属颗粒群的速度分布

陈亚红，白春华

（1.中北大学 化工与环境学院，太原030051；2.北京理工大学 爆炸科学与技术国家重点实验室，北京100081）

爆炸抛撒颗粒群研究涉及颗粒冲击动力学和高速两相流等领域，研究中存在某些重大困难。颗粒在冲击作用下的动力学响应非常复杂，会产生变形、相变或破碎［1］。由于颗粒数量巨大，跟踪并研究每个颗粒几乎是困难的［2］，有时也没有必要；而将颗粒看作连续相或均相材料则会掩盖许多细节，有时甚至是不可接受的［3］。在颗粒系统的研究中，统计方法的应用是重要手段之一。

爆炸驱动颗粒形成颗粒流的过程中，颗粒速度的分布是重要的。颗粒对靶板上的侵彻深度可反映颗粒速度。通过研究颗粒对靶板的侵彻深度的分布以及抛撒各阶段速度的变化规律，可得到爆炸抛撒颗粒群的速度分布。

1 爆炸抛散金属颗粒试验

装药方式如图1所示。

图1 装药方式示意图

装药中颗粒装填在Φ40mm×100mm的8701中心药柱（密度约1.6g／cm3）周围，上下端面与药柱的上下端面齐平。为了防止颗粒烧结，在其中混有少量分散剂。各装药的参数如表1所示，表中me，d，mg及δ分别为装药中中心炸药质量、金属颗粒特征尺寸、金属颗粒总质量及壳体厚度。

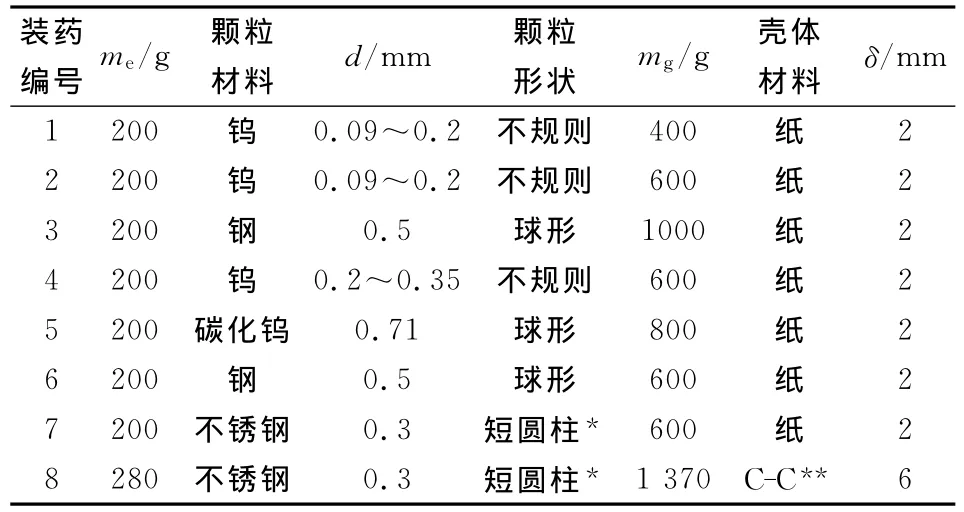
表1 装药参数

试验中用高速摄影机对爆炸驱动颗粒的过程进行记录和测量。装药悬挂固定，中心距地面高度约0.8m。在距装药2m、3m、4m、5m及6m处设立了槽钢柱，露出地面高度1m。各立柱与装药连线以20°角依次排开，防止相互遮挡。每个立柱上均在与装药同高的位置上固定了铝、肥皂及多层纸3种不同材料的靶板，对金属颗粒的着靶情况进行记录。现场布置如图2。

图2 现场布置图

2 试验结果

颗粒对不同材料靶板的侵彻情况如图3所示。多数颗粒在铝靶上的侵彻深度很小且相差不大，难以准确测量。颗粒在肥皂靶和纸靶上有足够深的侵彻深度，可反映颗粒群的速度分布。其中多层纸靶更便于设置、结果统计和保存。

图3 颗粒在不同靶板上的侵彻情况

由于更远距离上有些情况已不具有统计学条件（如着靶颗粒较少或侵彻深度太小等），故仅对各装药2m处纸靶的侵彻深度进行统计。对统计结果进行处理，各装药颗粒对靶板不同的侵彻深度的累积频度P和相应的分布拟合曲线如图4。第1，2，4号装药颗粒的侵彻深度服从指数分布，而其它装药基本服从正态分布。1，2，3，4，7，8号装药的分布拟合曲线（f1，f2，f3，f4，f7，f8）与累积频度之间有较高的符合度，而第5，6号的符合度较差。各装药颗粒的平均侵彻深度依次有5号＞6号＞3号＞7号＞8号＞4号＞1号＞2号。

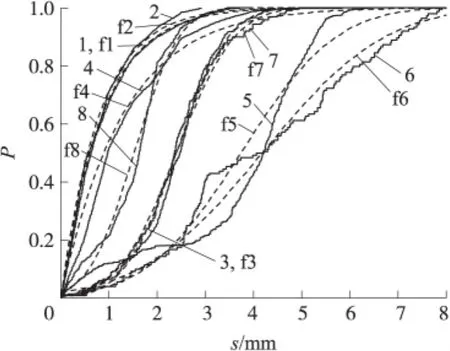
图4 各装药颗粒侵彻深度累积频度及相应分布拟合曲线

各装药颗粒对纸靶的侵彻深度的分布拟合后的参数如表2所示。

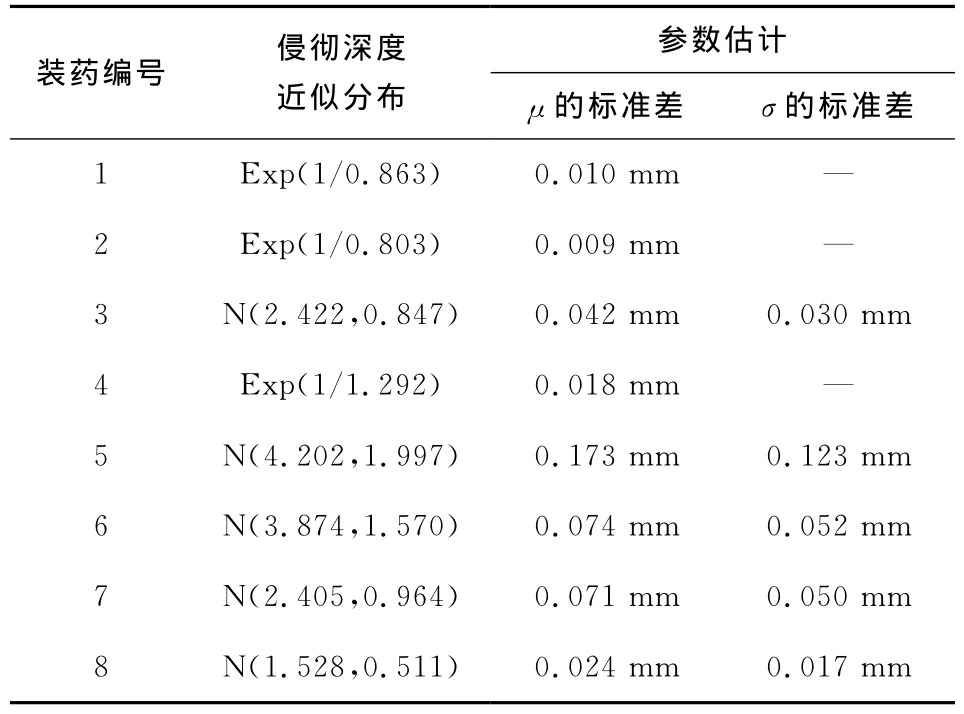
表2 侵彻深度分布拟合参数

3 分析与讨论

3.1 颗粒对靶板的侵彻规律

颗粒侵彻目标是一个复杂的过程，受颗粒的形状、质量、密度、强度及目标材料相关性质的影响，并且随颗粒速度的量级不同而呈现出不同的规律［4－5］。研究表明，在一定速度范围内（几十至几百m／s），近球形抛射体对半无限大低强度目标的侵彻深度与抛射体的着靶速度大致符合线性规律［6］。设颗粒对靶板的侵彻深度为s，着靶速度为v2，有：

式中：A、B为参数。

3.2 颗粒初速分布、着靶速度分布与侵彻深度分布间的关系

由随机变量函数的分布可知，颗粒的着靶速度有着与侵彻深度相同类型的概率分布，其概率密度为

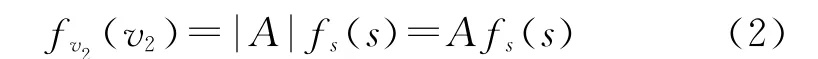
式中：fv2（v2）和fs（s）分别为着靶速度和侵彻深度的概率密度。

定义颗粒飞离爆轰产物时的速度v1为颗粒初速，颗粒速度随距离的衰减规律［7］：

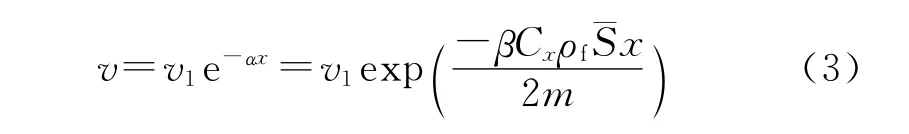
式中：βCxρf／（2m）＝α为衰减系数；v为颗粒存速；x为颗粒飞行距离；Cx为x处的标准（球形）空气阻力系数，一般取定值；ρf为空气密度为迎风面积，对球形取最大横截面积S；β为颗粒形状系数；m为颗粒质量。由式（3）可知，相同颗粒经过相同的距离x，存速v与初速v1间成线性关系。于是颗粒初速与着靶速度的分布类型相同，其概率密度间的关系为

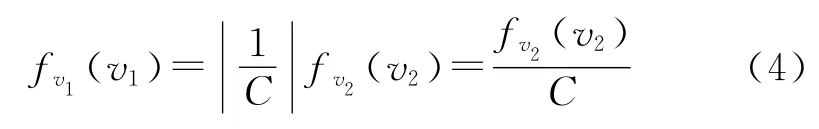
式中：C＝exp（－αx），fv1（v1）为初速的概率密度。

从试验结果和上述分析可知，1，2，4号装药颗粒初速和着靶速度也服从指数分布，而其它装药基本服从正态分布。由表2可知，各装药中金属颗粒的材料种类、尺寸及质量等参数组合各不相同，尤其是8号装药，其壳体材料及尺寸与其他装药有较大差别。但通过比较试验结果可以发现，在一定的装药比（颗粒总质量与炸药质量的比）范围内，颗粒的大小和形状是影响颗粒初速的主要因素。对d＜0.3mm的颗粒，初速近似服从指数分布，颗粒越小，分布越集中。对0.3mm以上的颗粒，初速近似服从正态分布，但随着粒径的增大，偏离也越来越大。这时，颗粒材料的密度和形状对初速分布的影响也增大。粒径为0.71mm的碳化钨颗粒的5号装药，侵彻深度在3～8mm间基本呈均匀分布，表明其初速在一定范围内也是呈均匀分布的。

3.3 初速分布形成原因探讨

设装药为无限长圆柱，中心为高能炸药，多层颗粒以同心圆筒形排列在中心药柱外，装药沿轴线同时起爆。壳体破裂前，颗粒受到爆轰波的强烈压缩，颗粒发生塑性变形，颗粒间剧烈碰撞和摩擦。随后壳体破裂，颗粒群和爆轰产物开始向外飞散。在颗粒群十分密集时，颗粒间的碰撞使得外层的部分颗粒获得较内层颗粒高的速度。当颗粒稀薄，没有颗粒之间的碰撞，仅受爆轰产物的作用，内层颗粒的速度将高于外层颗粒的速度。

粒径小于0.3mm的颗粒的惯性小，部分颗粒可能在壳体破裂前就达到其最大速度。壳体破裂后，这部分颗粒会在爆轰产物中受到阻力而减速，而那些速度低于爆轰产物速度的颗粒则加速，结果使颗粒群的速度趋于一致。由于爆轰产物的密度、压力和速度均衰减极快，颗粒会很快冲出爆轰产物的包围。由于惯性小，绝大多数颗粒都被同时加速，处于一个相对较窄的速度范围内。也有少部分颗粒因在爆轰产物中的位置有利而被加速到更高的速度。随着速度的增大，颗粒数减少，并且速度越高的颗粒，数量越少。颗粒初速总体成典型的指数分布。

在后续过程中，颗粒受到空气的阻力作用而减速。由式（3）可知，粒径小的颗粒速度衰减较大。需要指出的是，尽管颗粒着靶速度仍服从指数分布，在到达靶板时，那些质量较大、初速较低的颗粒的着靶速度可能反而较大。

对于粒径大于0.3mm的颗粒，由于颗粒的惯性较大，爆轰产物对其后续的加速效果较小，颗粒间因碰撞导致的动能传递更为有效。在多种效应的共同作用下，颗粒的速度服从正态分布。但随着粒径的继续加大，颗粒速度向平均分布的趋势变化。

试验还表明，颗粒的真实材料密度及装药比对颗粒速度的分布也有影响，但相对于颗粒的尺寸和形状，其影响较小。从3号与6号、7号与8号装药的结果比较看，装药比增大使颗粒速度分布由正态分布向指数分布变化。其原因是由于颗粒总质量的相对增大，单个的颗粒获得的动能将减少。设原来的颗粒群的侵彻深度近似成正态分布，减小颗粒速度会使部分颗粒不能侵彻靶板，部分仅在靶板表面生成小坑，其余部分颗粒的侵彻深度较大。总的效果是使得侵彻深度的频度曲线随侵彻深度增大成单调下降趋势，则分布近似为指数型分布。由于试验数据所限，具体的影响规律还需进一步研究。

比较7号和8号装药的穿深分布可知，强度高的壳体使颗粒的速度降低，对颗粒速度分布的影响与增加装药比相同。

4 结束语

在爆炸抛撒颗粒过程中，壳体破裂后爆轰产物对颗粒的后续加速作用不能忽略。这种作用对粒径小于0.3mm的颗粒更为明显。对于粒径大于0.3mm的颗粒，颗粒间的相互碰撞对颗粒速度的分布影响显著。颗粒的初速、固定距离上的着靶速度和对靶板的侵彻深度三者间有相同类型的分布。粒径小于0.3mm的颗粒，其初速分布为指数型；当粒径大于0.3mm时，在一定粒径范围内初速分布为正态型，粒径再继续增大，其分布向均匀型转变。

［1］程启华，李永新，卜雄洙.火药颗粒撞击应力测试技术［J］.弹道学报，2008，20（3）：20－23.CHENG Qi－hua，LI Yong－xin，BU Xiong－zhu.Measurement technology of percussion force of powder grains［J］.Journal of Ballistics，2008，20（3）：20－23.（in Chinese）

［2］胡建新，夏智勋，刘君.颗粒轨道模型中颗粒跟踪与定位算法研究［J］.弹道学报，2005，17（2）：82－87.HU Jian－xin，XIA Zhi－xun，LIU Jun.Overview of particle locating algorithm for Eulaerian－Lagrangian computations of twophase flow［J］.Journal of Ballistics，2005，17（2）：82－87.（in Chinese）

［3］吴清松，胡茂彬.颗粒流的动力学模型和实验研究进展［J］.力学进展，2002，32（2）：205－258.WU Qing－song，HU Mao－bin.Advances on dynamic modeling and experimental studies for granular flow［J］.Advances in Mechanics，2002，32（2）：205－258.（in Chinese）

［4］CORBETT G G，REID S R，JOHNSON W.Impact loading of plates and shells by free－flying projectiles：a review［J］.International Journal of Impact Engineering，1996，18 （2）：141－230.

［5］文鹤鸣.混凝土靶板冲击响应的经验公式［J］.爆炸与冲击，2003，23（3）：267－274.WEN He－ming.Empirical equations for the impact response of concrete targets［J］.Explosions and Shock Waves，2003，23（3）：267－274.（in Chinese）

［6］尹放林，严少华，钱七虎，等.弹体侵彻深度计算公式对比研究［J］.爆炸与冲击，2000，20（1）：79－82.YIN Fang－lin，YAN Shao－hun，QIAN Qi－hu，et al.Contrast analysis on calculation of penetration depth of projectile［J］.Explosions and Shock Waves，2000，20（1）：79－82.（in Chinese）

［7］爆炸及其作用编写组.爆炸及其作用［M］.北京：国防工业出版社，1979.