导弹无依托待发射阶段场坪准静态响应研究

周晓和，王惠方，马大为，高 原，任 杰

（1.南京理工大学 机械工程学院，南京210094；2.中国兵器工业第202研究所，陕西 咸阳712099；3.第二炮兵装备研究院，北京100094）

近年来，由于空间侦察技术和导弹命中精度的不断提高，战略战术导弹采用地下井式热发射及通过增加地下井的抗超压能力来保护导弹的方法变得越来越不可靠。因此，一些国家在进一步加固地下井的同时，相继研制出了各种陆基机动发射方式［1－2］。无依托发射是指导弹发射不再依托预准备的发射场地，而是随机选取场地发射，该方式具有机动地域广阔、速度快、生存能力高和攻击能力强等特点［3］。我国公路修筑覆盖面广阔且错综复杂，将其作为导弹无依托发射场坪不仅能提高导弹发射的机动性、随机性，更为导弹发射提供了足够的隐蔽性。

导弹的公路发射要求在各等级公路上均可实现安全发射，但我国公路仍存在性能较差的路面（如三级、四级公路），在导弹完成起竖后，由于发射系统整体质心的后移，将导致前、后支腿处场坪受力的不同，该现象将影响导弹发射精度及发射平台整体的稳定性［4－5］，故进行导弹待发射时段场坪与发射平台间的耦合效应研究显得尤为重要。姚晓光［6－7］对导弹起竖阶段发射车整体响应及受力情况做了详尽的分析，并未涉及导弹待发射阶段的力学分析；程洪杰［8］将场坪元素做为发射平台中的重要组成部分，并通过理论计算得到导弹无依托发射各阶段场坪受力的计算公式，并没有涉及具体的混凝土面层本构关系，因此无法对待发射阶段场坪响应进行详尽的研究。

待发射阶段是指发射车完成调平与导弹起竖后至导弹点火时段，本文将发射场坪视为发射系统中的重要组成部分，采用扩展的线性Drucker－Prager本构［9］模拟沥青混凝土面层，完成无依托发射场坪数值模型的建立，并对待发射阶段下支腿处场坪的准静态响应、产生塑性变形的条件及蠕变效应和塑性应变间的关系进行了研究与分析。研究结果可为导弹无依托发射前场坪快速评估提供理论支撑。

1 扩展的线性Drucker－Prager本构

1.1 屈服函数

图1为扩展的线性Drucker－Prager本构在子午面上的屈服轨迹，图2为该本构模型在π平面上屈服／流动面，其屈服准则表达式为［10］

式中：β为p－T平面上线性屈服轨迹的倾角，即材料的摩擦角；p为等效压应力；d为材料的粘聚力；T为偏应力参数，其定义式为

式中：q为Mises等效应力；r为偏应力第三不变量；K为三轴拉伸屈服应力与三轴压缩屈服应力之比。

图1 子午面上屈服轨迹

图2 π平面上的屈服／流动面

线性模型中，材料发生塑性应变会引起塑性流动，塑性流动势G表达式为

式中：ψ为p－T平面上的剪胀角。

假定材料采用非相关联流动法则，则塑性应变的方向与线性塑性流动势函数G正交，则有：

式中：εpl为塑性应变；¯εpl为等效塑性应变；c为与硬化参数相关的常量；σ为应力张量。

1.2 蠕变模型

假设存在应力点的蠕变等倾面，此等倾面上具有相同的蠕变“强度”，且由等效蠕变应力确定。当材料发生塑性变形时，等效蠕变面与屈服面一致，故等比例缩小屈服面可得到等效蠕变面。在p－q平面上，蠕变面和屈服面相互平行，如图3所示。当材料受单轴压缩时，等效蠕变应变可表示为［11］

当材料受单轴拉伸时，等效蠕变应变¯σcr可表示为

蠕变应变率采用塑性应变率的双曲线流动势函数，其表达式为［11］

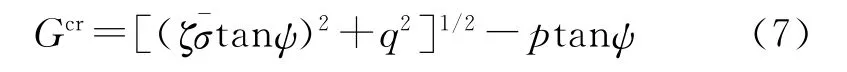
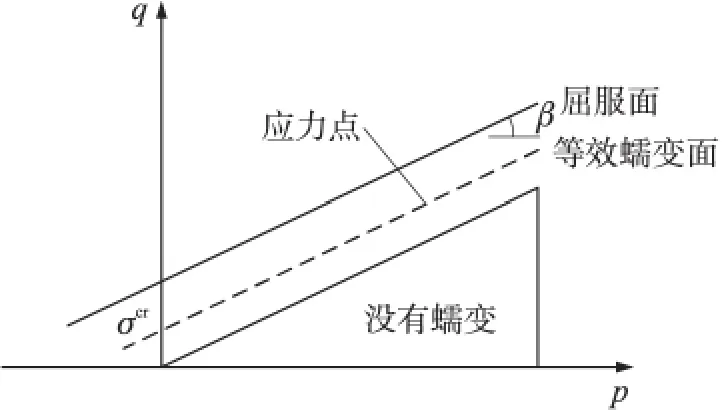
图3 等效蠕变应力定义为剪应力示意图

1.3 蠕变法则的定义

当材料所受应力保持不变时，可采用“时间硬化”幂函数定义材料的蠕变法则，其表达式为［12］

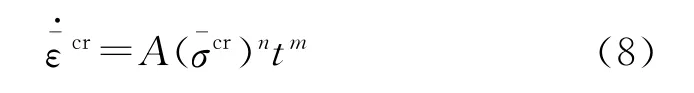
2 无依托发射场坪数值模型

取沥青混凝土四级公路为研究对象，建立无依托发射场坪平面数值模型，如图4所示，图中X、Y和Z轴方向分别为发射场坪横向、垂向和纵向。发射场坪平面数值模型从上至下依次为沥青混凝土面层、基层、底基层及土基；根据载荷对称原理假定左右支腿处场坪受力相同，故取发射场坪的1／2进行研究，完成对数值模型的合理简化，依据《公路沥青路面设计规范》（JTG D50－22006）和《公路工程技术标准》（JTJ001－97），发射场坪平面数值模型宽取2 250mm，高取2 140mm；考虑真实道路结构，在发射场坪平面数值模型土基层的底部施加固端约束，左侧边缘施加沿Z轴对称的边界条件，右侧土基边缘施加沿Z轴对称的边界条件，面层、基层和底基层右侧边缘均为自由边界。

沥青混凝土层采用扩展的线性Drucker－Prager本构中的蠕变模型进行模拟，其材料参数如表1所示，其中摩擦角β和沥青混凝土初始屈服应力σ0c取值可由Mohr－Coulomb本构的内摩擦角φ和粘聚力c经过换算得到，β和的计算公式为［11］

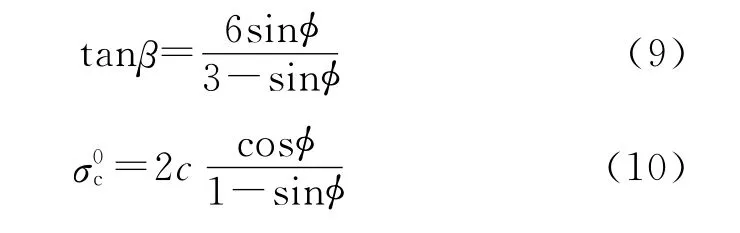
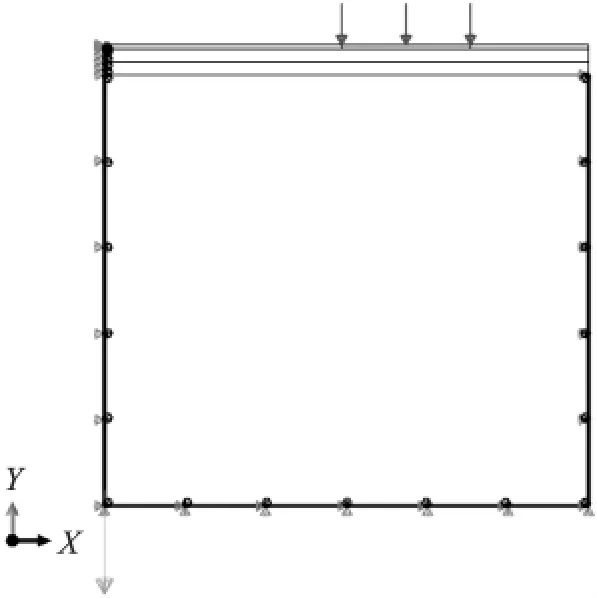
图4 发射场坪数值模型

表1 沥青混凝土面层材料参数

沥青混凝土材料的蠕变参数可由三轴试验数据通过拟合得到，分析时不考虑温度对场坪性能的影响，取20℃时的沥青混凝土蠕变参数进行导弹待发射阶段场坪粘弹塑性分析［13］，蠕变参数为A＝5.631 4×10－4，n＝1.0，m＝－0.802。

为重点研究发射场坪在导弹待发射阶段时的准静态响应及沥青混凝土面层的粘弹塑性响应，将基层、底基层及土基均设置为线弹性材料，结构参数及材料参数［14－15］如表2所示。表中H、E、μ、ρ分别为发射场坪不同功能层的厚度、回弹模量、泊松比及质量密度。

表2 发射场坪各功能层材料参数及结构参数

当导弹处于待发射阶段时，发射场坪所受载荷主要为场坪自身重力和来自液压支腿的压力载荷，其中场坪自身重力以重力场的形式施加于整个数值模型；液压支腿的压力载荷以压强分段函数的方式施加于液压支腿处场坪；假设待发射阶段持续时间为1 800s，在对前液压支腿处场坪的分析中（简称工况一），压强在1s内从0线性增加至0.03MPa后维持压强集度至1 800s，在对后液压支腿处场坪的分析中（简称工况二），压强在1s内从0线性增加至0.8MPa，并维持压强集度至1 800s。

为提高数值计算的精度，将发射平台处于垂直待发状态时液压支腿处场坪受载分析过程分为2个分析步：

①场坪应力场计算分析步。该分析步主要建立初始应力场平衡，对于发射场坪数值模型，初始应力场即为自重应力场，其竖向应力随深度呈线性变化。该分析步中只加载重力载荷，计算后获得与给定边界条件和载荷相平衡的应力状态，并将其作为后续分析步的初始应力场。

②发射场坪待发射阶段准静态分析步。此分析步主要模拟导弹处于垂直待机状态时，发射平台前、后液压支腿处场坪的粘弹塑性响应，并以液压支腿作用区域的应力、沉降、蠕变应变和塑性应变评判沥青混凝土场坪的力学性能。该分析步在1s内将压强从0增加至最大值，之后保持均布载荷作用至1 800s。

3 结果与分析

3.1 前、后支腿处场坪应变

图5和图6分别为工况一和工况二中支腿处场坪塑性应变能Wpl及加载中心点垂向塑性应变εpl曲线。由图可知，工况一中场坪未产生塑性应变能，故工况一中场坪未发生塑性应变。这是因为前支腿处场坪所受应力σ未达到沥青混凝土面层的初始屈服应力，故材料不发生屈服，此时总应变由弹性和粘性应变两部分组成，其中弹性应变可表示为

式中：εel为弹性应变。粘性应变可表示为

式中：εcr为粘性应变。

此时前支腿处场坪所产生的总应变ε可表示为

工况二中场坪在加载开始后迅速发生了塑性屈服，并产生了塑性应变。这是因为后支腿处场坪所受应力σ大于沥青混凝土面层的初始屈服应力σ0c，材料发生屈服，此时后支腿处场坪所产生的总应变由弹性、粘性和塑性应变三部分组成，其表达式为

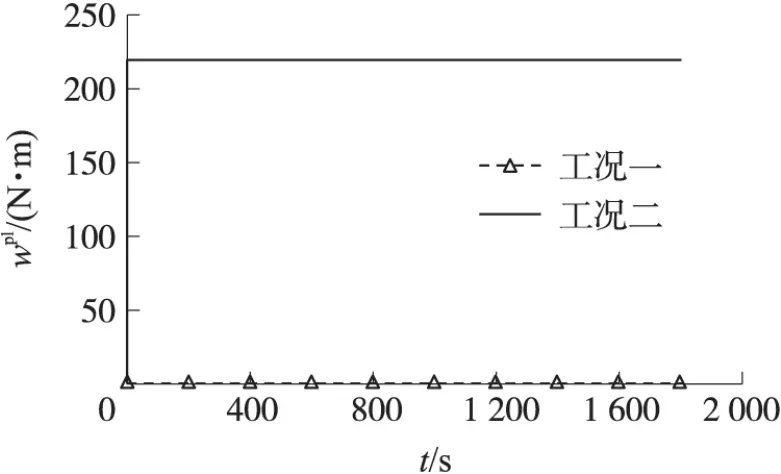
图5 塑性应变能曲线

图6 加载中心点垂向塑性应变曲线

当保持前、后支腿处场坪所受应力σ不变时，材料的粘性行为主要表现为蠕变，而不是松弛。图7和图8分别为工况一和工况二中支腿处场坪蠕变应变能Wcr及加载中心点垂向蠕变应变曲线εcr，由图可知，前、后支腿处场坪从开始加载就产生蠕变应变能。工况二下场坪蠕变应变能及蠕变应变均大于工况一，这是因为工况二下场坪发生塑性应变，由式（8）得，此时后支腿处场坪面层的等效蠕变应变率¯ε·cr将大于前支腿处场坪面层的等效蠕变应变率，故前、后支腿处场坪面层在相同的载荷作用时间下，工况二场坪蠕变应变能和蠕变应变均大于工况一场坪。

图7 蠕变应变能曲线

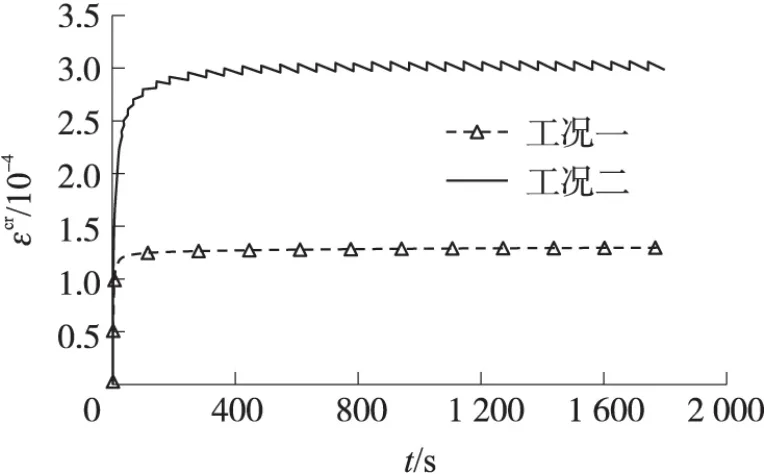
图8 加载中心点垂向蠕变应变曲线

3.2 前、后支腿处场坪沉降

图9 为工况一和工况二下支腿处场坪加载中心点垂向位移s2的曲线图。在载荷作用下工况一的加载中心点下沉了1.52mm，工况二中加载中心点下沉了19.33mm，说明导弹发射平台处于垂直待发射时，后液压支腿处场坪下沉量比前液压支腿处场坪下沉量大，发射平台整体呈前高后低，这将对无依托发射时的导弹出筒姿态及发射车整体稳定性造成一定的影响。

图9 加载中心点垂向位移曲线

3.3 前、后支腿处场坪应力分布

图10 和图11分别为工况一和工况二在1 800s时刻发射场坪Y方向应力云图。由图可知，两种工况下Y方向应力云图规律相似。计算载荷在整个加载过程中恒定且沥青混凝土面层厚度较小，这导致场坪面层及基层受力连续，且场坪材料在各功能层交界面处节点连续，从而导致场坪面层与基层在加载面范围内Y方向应力相差较小。

两种工况下发射场坪在Y方向的最大应力点位于场坪右侧边界、底基层与土基交界面处，这是因为数值模型中面层、基层和底基层右侧边缘为自由边界；在支腿静载荷作用下，受载区域场坪表现为局部下沉，场坪整体呈里凹外翘，故发射场坪右侧边界、底基层与土基交界面处发生了剪切变形。

图10 1 800s时工况一场坪Y方向应力云图

图11 1 800s时工况二场坪Y方向应力云图

4 结论

本文采用扩展的线性Drucker－Prager本构对沥青混凝土面层进行了建模，完成了无依托发射场坪数值模型的建立，研究了发射平台前、后支腿处场坪准静态响应，对支腿处场坪发生塑性变形的条件进行了探讨，对支腿处场坪发生塑性应变与蠕变应变间的关系进行了分析，并对导弹无依托待发射阶段支腿处场坪沉降和应力分布进行了研究，得到以下结论：

①导弹处于垂直待发射状态时，发射平台前支腿处场坪所受应力由于未达到沥青混凝土面层初始屈服应力，材料未发生屈服，故前支腿处场坪只发生了弹性及粘性应变；发射平台后支腿处场坪所受应力大于沥青混凝土面层初始屈服应力，材料发生屈服，故后支腿处场坪发生弹、粘及塑性应变。

②发射平台后支腿处场坪由于产生塑性应变分量，其总应变值大于前支腿处场坪的总应变值，故后支腿处场坪面层的等效蠕变应变率将大于前支腿处场坪面层的等效蠕变应变率，前、后支腿处场坪在相同的载荷作用时间下，后支腿处场坪蠕变应变能和蠕变应变均大于前支腿处场坪。

③导弹处于垂直待发射状态时，后支腿处场坪局部沉降明显，且沉降值大于前支腿处场坪，发射平台整体呈前高后低；前、后支腿处场坪应力连续，最大应力点位于场坪右侧边界、底基层与土基层交界面处。

［1］SPEARMAN M L.Innovation in aerodynamic design features of soviet missiles，NASA 20080014230［R］.2008.

［2］SEOW Y W.Survivability enhancement in a combat environment，ADA429875［R］.2004.

［3］程洪杰，钱志博，赵媛，等.导弹起竖过程中的对地荷载研究［J］.兵工自动化，2011，30（11）：1－3，19.CHENG Hong－jie，QIAN Zhi－bo，ZHAO Yuan，et al.Study on the load to ground on missile erection process［J］.Ordnance Industry Automation，2011，30（11）：1－3，19.（in Chinese）

［4］刘达，顾克秋，何永.基于不同土体的牵引火炮动态应力分析［J］.南京理工大学学报，2008，32（6）：681－685.LIU Da，GU Ke－qiu，HE Yong.Dynamic stress analysis of towed howitzer placed on different soils［J］.Journal of Nanjing University of Science and Technology，2008，32（6）：681－685.（in Chinese）

［5］韩世东，李军，孙延超，等.某火箭射击精度受土壤硬度影响分析［J］.四川兵工学报，2012，33（1）：41－42，65.HAN Shi－dong，LI Jun，SUN Yan－chao，et al.The effect of the soil hardness on the firing accuracy of a rocket［J］.Journal of Sichuan Ordnance，2012，33（1）：41－42，65.（in Chinese）

［6］姚晓光，郭晓松，冯永保，等.导弹起竖过程的载荷研究［J］.兵工学报，2008，29（6）：718－722.YAO Xiao－guang，GUO Xiao－song，FENG Yong－bao，et al.Load analysis on missile erection［J］.Acta Armamentarii，2008，29（6）：718－722.（in Chinese）

［7］姚晓光，郭晓松，冯永保，等.导弹起竖系统的仿真研究［J］.兵工学报，2007，28（1）：23－27.YAO Xiao－guang，GUO Xiao－song，FENG Yong－bao，et al.Simulation and research on missile erecting system［J］.Acta Armamentarii，2007，28（1）：23－27.（in Chinese）

［8］程洪杰，钱志博，赵媛，等.导弹无依托发射场坪承载能力分析［J］.起重运输机械，2011（12）：48－52.CHENG Hong－jie，QIAN Zhi－bo，ZHAO Yuan，et al.Analysis of launching site load－carrying ability for missile unsupported random launch［J］.Hoisting and Conveying，2011（12）：48－52.（in Chinese）

［9］杨强，冷旷代，张小寒，等.Drucker－Prager弹塑性本构关系积分：考虑非关联流动与各向同性硬化［J］.工程力学，2012，29（8）：165－171.YANG Qiang，LENG Kuang－dai，ZHANG Xiao－han，et al.An integration algorithm for drucker－prager elastic－plastic model with non－associated flow rule anisotropic hardening［J］.Engineering Mechanics，2012，29（8）：165－171.（in Chinese）

［10］张丽娟，张肖宁，陈页开.沥青混合料变形的粘弹塑性本构模型研究［J］.武汉理工大学学报（交通科学与工程版），2011，2：289－292.ZHANG Li－juan，ZHANG Xiao－ning，CHEN Ye－kai.Viscoelasto plastic constitutive model of deformation for asphalt mixtures［J］.Journal of Wuhan University of Technology（Science and Engineering），2011，2：289－292（in Chinese）

［11］王金昌，陈页开.ABAQUS在土木工程中的运用［M］.杭州：浙江大学出版社，2006：34－35.

［12］张久鹏，黄晓明，王晓磊.基于粘弹塑性理论的沥青混凝土路面车辙分析［J］.公路交通科技，2007，24（10）：20－24.ZHANG Jiu－peng，HUANG Xiao－ming，WANG Xiao－lei.Analysis of asphalt pavement rut based on elastic－viscoplastic theory［J］.Highway Traffic Science and Technology，2007，24（10）：20－24（in Chinese）

［13］郑健龙，田小革，应荣华.沥青混合料热粘弹性本构模型的实验研究［J］.长沙理工大学学报，2004，1（1）：1－7.ZHENG Jian－long，TIAN Xiao－ge，YING Rong－hua.A laboratory research on the thermo－visoelastic constitutive model of bituminous mixtures［J］.Journal of Changsha University of Science and Technology，2004，1（1）：1－7.（in Chinese）

［14］柳志军，刘春荣，胡朋，等.土基回弹模量合理取值试验研究［J］.重庆交通学院学报，2006，25（3）：62－64.LIU Zhi－jun，LIU Chun－rong，HU Peng，et al.Experiment study on reasonable evaluation of rebound modules of subgrade［J］.Journal of Chongqing Jiaotong College，2006，25（3）：62－64.（in Chinese）

［15］王金昌，朱向荣.软土地基上沥青混凝土路面动力分析［J］.公路，2004（3）：6－11.WANG Jin－chang，ZHU Xiang－rong.Dynamic analysis of asphalt concrete pavement on soft clay ground［J］.Highway，2004（3）：6－11.（in Chinese）