期限溢价、超额收益与宏观风险不确定性——基于银行间国债市场的分析

王晓芳 郑 斌

一、引 言

期限溢价是利率期限结构研究的核心问题。随着我国利率市场化推进以及货币政策向价格调节机制的转变，期限结构所包含的市场预期属性愈发受到政策制定者和投资者的关注。期限溢价作为利率预期的风险补偿，反映了市场主体对未来宏观风险的度量。在以往众多研究文献中，多数学者并没有严格定义和区分期限溢价和超额收益，而将两者统一定义为期限溢价。郑振龙、吴颖玲(2009)提出期限溢价应代表当期市场对未来风险预期的无偏估计。相比之下，超额收益则应为事后市场风险收益的综合评估，其不具有预期属性。关于期限溢价和超额收益的研究，早期的文献依托于回归预测的分析方法，通过收益率曲线形状因子(水平、斜率、曲率)间接反映市场期限溢价水平。Fama(1984)、Fama 和Bliss(1987)以及Campbell 和Shiller(1991)最早通过长短利差、远期利率与短期利率利差对超额收益进行预测。Cochrane 和Piazzesi(2005)在Fama、Bliss 等研究基础上，创新性地使用远期利率线性组合作为收益预测因子，发现其具有更高的超额收益预测能力。我国也有学者研究收益率曲线形状特征因子的预测能力，如朱世武、陈建恒(2004)研究发现长短期收益率差对于超额收益的预期能力较强。王安兴、余文龙(2010，2012)则对收益率曲线三种形状特征因子的超额收益预测能力进行综合分析，发现收益曲线的第一、第二主成分构成的单一预测变量可以很好地预测债券超额收益。除期限结构形状因子外，一些学者将宏观因子引入回归分析中。Ludvigson 和Ng(2009)在对132 个宏观变量进行处理分析后发现，实际产出、就业、通胀以及股市信息对美国国债超额收益的影响较为突出。我国学者董莉莎、朱映瑜(2011)使用面板回归分析发现除基准利率影响不显著外，通胀、M2 增长率对超额收益具有显著正向影响，而规模以上工业增长值和上证指数收益率则为负向影响。

回归分析虽然能直观反映超额收益变动中潜在影响因素和经济政策动因，但依托于回归系数的期限溢价估计往往存在着较大的偏差①由于市场并非处于无套利环境，期限结构远期利率预测表征的是市场真实测度(P 测度)下的预测值。由于OLS 方法无法进行测度转换(向Q 测度转换)即实现市场中性，因此通过回归方法的期限溢价估计在理论层面具有明显的偏误。(Chernov 和Mueller，2012)。鉴于此，学者们试图通过动态模型方法实现市场中性条件下的期限溢价估计。Fisher(1998)、Duffee(2002)及Dai 和Singleton(2002)将时变期限溢价引入高斯期限结构模型，形成了以动态期限结构模型分析期限溢价的研究范式。Kim 和Wright(2005)、Cochrane 和Piazzesi(2008)等在上述研究的基础上，基于理性预期理论，使用收益曲线形状特征因子构建仿射期限结构模型，并成功将长期收益率分解为预期未来利率与期限溢价。我国学者郑振龙、吴颖玲(2009)使用3 因素仿射期限结构模型对银行间市场和交易所国债期限溢价进行了提取和分析。伴随期限溢价研究的推进，学者们逐渐意识到模型出色的拟合能力并不能掩盖其经济含义的匮乏。Dewachter 和Lyrio(2006)在其研究中就提出期限结构的研究不应该只局限于收益曲线变动的表象，更应集中于这些潜在因素背后的经济动力。Ang 和Piazzesi(2003)最早将通胀和实际经济活动指标引入仿射期限结构模型，形成了无套利宏观金融模型的研究方法。Law(2004)使用无套利宏观金融模型发现期限溢价变化来源于实体经济行为、通胀以及货币政策。Ang、Dong 和 Piazzesi(2005)在无套利宏观金融模型的估计结果中发现短期利率水平和产出增长与期限溢价在统计上具有极强的联系性。Rudebusch、Swanson 和Wu(2006)使用无套利宏观金融模型在对美国10 年期国债收益率分解中发现，除消费、产出缺口、通胀外，欧洲美元利率和标准普尔500 指数对期限溢价具有影响。Duffee(2007)通过构建无套利宏观金融模型对宏观因素与期限溢价关联性进行分析，结果发现溢价变动受通胀、经济增长和短期利率的影响较大。Piazzesi、Salomao 和Schneider(2013)则在对美国数据研究发现期限溢价的低频部分包含了较多的商业周期信息，且具有明显逆周期特征。从上述研究可以看到，国外学者对于期限溢价内含宏观风险特征研究较为全面，多数文献认为通胀、经济活动和货币政策是影响期限溢价形成和波动的重要因素。相比而言，我国学者并没有对期限溢价内含宏观风险特征进行深入研究和总结，多数研究①如张蕊等(2009)将流动性变量作为仿射模型因子引入模型估计中，分析了流动性对期限结构变动的影响。孙皓、石柱鲜(2011)使用广义均衡下的宏观金融模型分析需求、供给以及潜在产出对期限结构影响的机制。陈守东、王妍(2014)、何晓群、王彦飞(2014)以及金雯雯等(2014)在DNS 模型(动态Nelson-Siegel 模型)的框架上，使用VAR(TVP-VAR)模型分析宏观因素与模型隐因子之间的影响关系。另外的研究如刘金全等(2007)、杨小军(2008)、于鑫(2009)、范龙振和张处(2009)使用VAR 模型研究供给、价格、宏观政策对期限结构变动的影响。集中于期限结构整体的宏观风险特征上，忽视了期限溢价对于市场风险的表征作用。

鉴于此，本文在已有文献研究的基础上，通过模型化的方法估计市场期限溢价，进一步研究市场溢价预期的形成和变动特征，并对其波动的机理进行理论探讨，补充和深化既有研究。本文所做的工作为以下三个方面。第一，当前诸多的期限结构模型具有较好的拟合效果(例如DNS 模型)，但对于期限溢价估计的偏差较大②这主要由于多数仿射期限结构模型并没有处理短期利率拟合误差，通常使用DNS 模型没有进行市场中性的测度转换。。因此本文在估计过程中通过消除短期利率拟合误差，力求准确地测算当期市场期限溢价水平，反映市场预期。考虑到广义均衡模型在实际应用中不如无套利均衡模型对利率波动的捕捉能力，本文使用无套利宏观金融模型，这是本文研究的基础。第二，期限溢价作为市场对未来风险不确定性的补偿，间接反映了市场对于未来系统性风险的判断，其本身具有预期属性。多数研究③Smant(2010)、李宏瑾(2012)将时变期限溢价特征引入预期理论检验中。将期限溢价作为期限结构预期理论检验的调整项或补充项，忽略了溢价本身的预期特征。本文将对比期限溢价和超额收益统计数据，对期限溢价预期特征进行深入分析。第三，为了进一步分析期限溢价受宏观经济政策影响的机理，本文将通胀、经济活动和货币政策变量作为无套利宏观金融模型的模型因子，通过构建状态空间模型深入研究期限溢价受宏观风险影响的机制。本文还将依据预期理论，尝试性的从新的视角对期限溢价波动的机理进行理论性探讨。

本文的具体研究结构如下：第二部分构建基于时变期限溢价的无套利宏观金融模型；第三部分进行数据选取与处理，对模型进行估计；第四部分对期限溢价的预期特征进行分析，并通过构建状态空间模型，研究宏观风险对期限溢价的动态影响，对结果进行理论解释。第五部分是对本文研究进行总结并提出政策建议。

二、无套利宏观金融模型构建

1. 状态转移过程

在宏观因子的选择上，本文从通胀、经济活动以及货币政策因素3 个方面选取指标。通货膨胀指标选用CPI 变化率对数值。而在实际经济活动变量选择上，多数文献选择实际GDP 变化率，Ang、Piazzesi(2003)使用了包括就业、消费、工业产出等表征宏观活动的因素，Duffee(2012)运用产出缺口和消费作为经济活动变量。考虑到我国经济的复杂性，单纯使用实际GDP 变化率并不能全面地表征宏观经济活动状态，同时消费并非拉动经济增长的主要动力。为了使变量具有权威性和实用性，本部分选用宏观经济景气指数(规模以上工业产出具有很强的经济状态表征能力)作为实际经济活动变量。根据期限溢价的需要，本部分依据Dai 和Singleton(2000)提出的隐因素不变转换(Invariant Transformations)的方法，借鉴Evans 和Marshall(2002)及Duffee(2007)将模型中的隐因素转换为短期利率和其他隐因素的做法，将短期利率引入宏观因子向量，这样模型就舍去无套利宏观金融模型中短期利率的仿射关系，而模型中隐因子则作为传统仿射模型的残差项表征国债期限溢价特征信息。

本部分宏观因子向量如下：

其中，πt、gt、rt分别表示通胀、宏观经济活动和短期利率。Duffee(2011)认为考虑测量误差对于识别模型十分重要，这里波浪号表示宏观因素在模型估计后除去测量误差的部分。

模型中使用3 个隐因子组成的向量 ωt作为溢价向量，并假定隐因子变量和宏观变量之间相互独立。两者组成的状态向量为：

状态向量 xt服从马尔可夫状态转移过程。其离散化方程参照高斯向量自回归形式。其动态过程表示为：

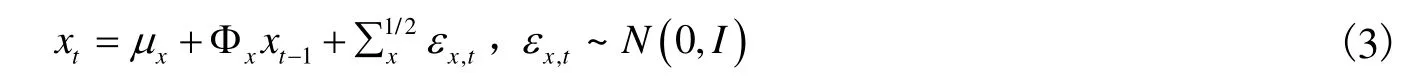
等式中各矩阵具体形式如下：

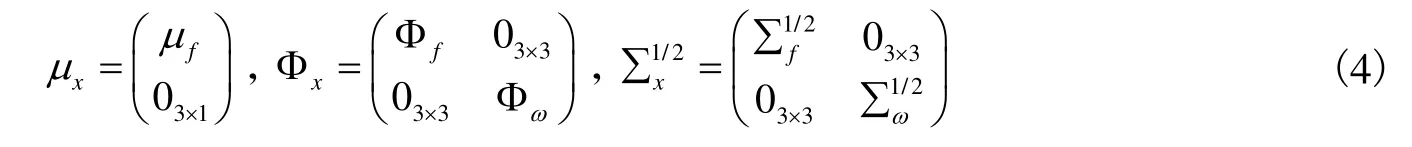
模型估计的前提是上述动态过程为稳态过程，即 Φx存在逆矩阵，等式中 μx可表示为状态变量 xt的无条件均值，公式如下：

状态转移矩阵 Φx为6*6 矩阵，Φf和Φω分别为宏观变量和隐因子变量的转移矩阵。∑x为状态向量的方差协方差矩阵，本部分参考Joslin 等(2011)做法，将 ∑x进行下三角乔列斯基分解，使得 εx,t中的各冲击量线性无关，使得冲击向量矩阵I 为对角阵。

2. 定价核与观测过程

债券定价服从单位价格债券的等价鞅过程，其表示为：

h 为数据周期长度，λt为t 时刻的市场风险价格为詹森不等式调整项。λt满足状态向量的仿射形式如下：

其中，λ0为长度为6 的列向量，表示为， λ1则为6*6 矩阵，为：λ1=根据上文中不变转换结果，本部分参考Bikbov 和Chernov(2010)的方法，将风险价格方程中隐因子向量 ωt分别作为各宏观因素解释的残差部分，其形式为：

将状态转移方程进行等价鞅转换：

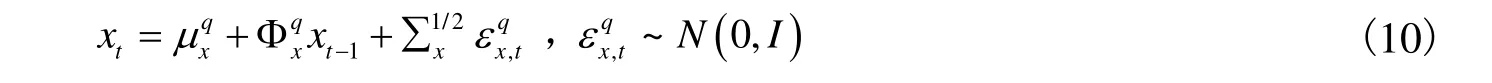
债券价格可以由调整后的风险中性状态转移矩阵表示为状态向量的仿射形式。

其中，

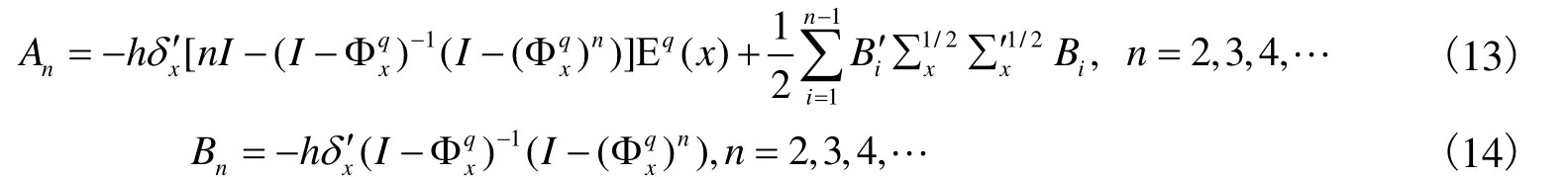
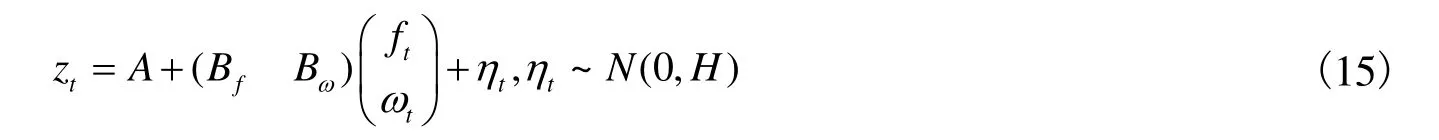
其中，zt为d 维年化收益率列向量，H 矩阵为对角阵。

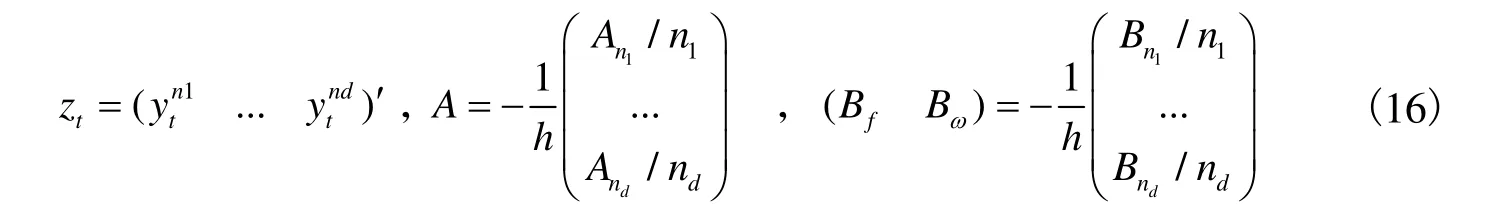
3. 超额收益分解

Fama 和Bliss(1987)等文献对超额收益的定义，其表达式为：

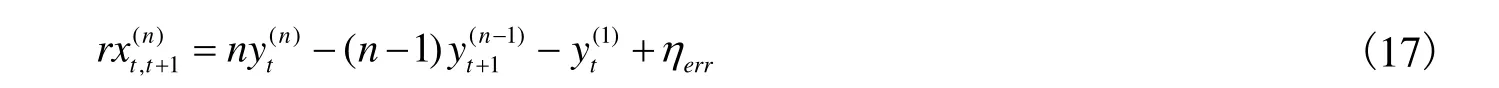
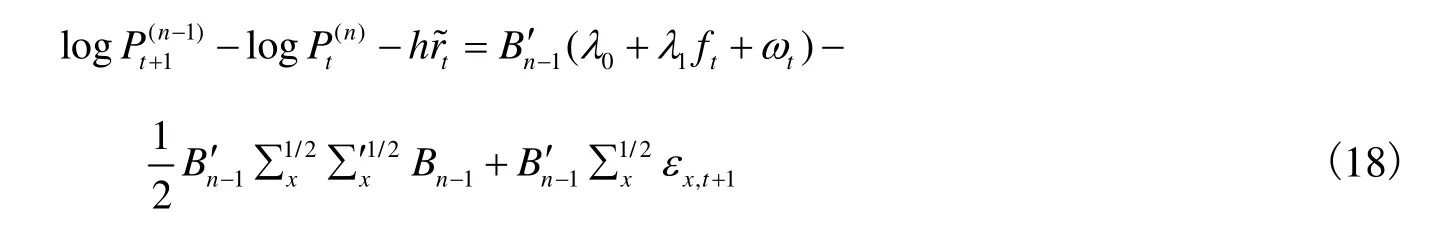
上 式 右 侧 为 超 额 收 益 的 随 机 贴 现 因 子 形 式，为 期 限 溢 价，为调整项，为冲击项。

超额收益的方差表达式为：

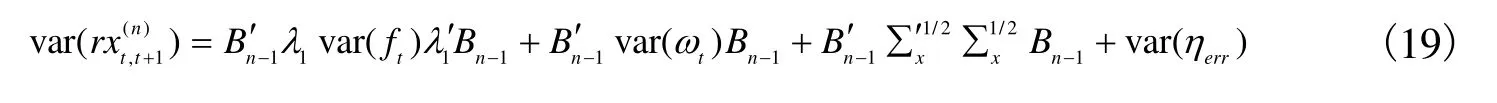
该式中前两项为t 时刻模型预期溢价的方差，第三项为t+1 时刻状态变量冲击的方差，第四项为测量误差项。方差分解中的成分比重可通过判定系数 R2求取。

三、样本数据采集与模型估计

1. 数据采集和处理

中央登记结算公司银行间国债即期收益率数据包括市场双边报价、柜台交易等各方面国债交易信息，数据覆盖面比较广，并且在数据制作过程中，对异常点进行了科学处理，能够很好反应市场价格情况。因此本文选择中央登记结算公司2006 年3 月至2014 年4 月共98 个月的银行间国债即期收益率月度加权平均数据，分别选用1 年、2年、3 年、5 年、7 年、10 年6 个期限品种。在宏观变量的选取上，本文首先选取wind 数据库月度CPI 环比指数作为通胀指标，以2006 年2 月为基期，通过Census X12 ARIMA 进行季度调整，并将调整后的数据转化为 ΔCPI 形式。在宏观经济活动指标的选取上，本文收集了98 个月的宏观经济景气指数(一致指数)数据，由于指数在编制过程中进行了X11 季度调整，所以本文直接将指数数据转化为 Δ ME BCI 变化率形式。无风险短期利率选择上，国外多数学者使用3 月期国库券利率或3 月期TIPS 债券作为短期利率代表，鉴于我国通胀水平高于西方国家，并且缺乏类似TIPS 等通胀保值债券产品，为了尽可能消除作为模型因子的短期利率中的通胀因素，本文舍弃了通常使用的3 个月期国债收益率作为无风险短期利率的做法，选择中央登记结算公司期限为1月期国债收益率数据作为代替。

2. 模型估计和结果

根据Duffee、Stanton(2004)和de Jong(2000)等研究成果，卡尔曼滤波极大似然估计是研究仿射模型最为有效的方法，因此本文也采用这一方法对模型参数进行估计。估计预测过程中，本文将无风险短期利率数据固定(即数据模型估计误差为0)，保证期限溢价数据的真实性。在似然函数估计中，研究根据Bikbov 和Chernov(2010)的方法，对似然函数引入惩罚项(penalization term)，公式为：

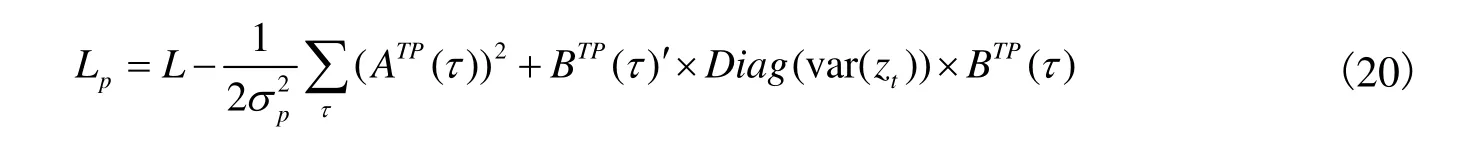
其中，ATP(τ )和 BTP(τ )为期限溢价仿射系数，τ 为债券期限，仿射系数满足下式：

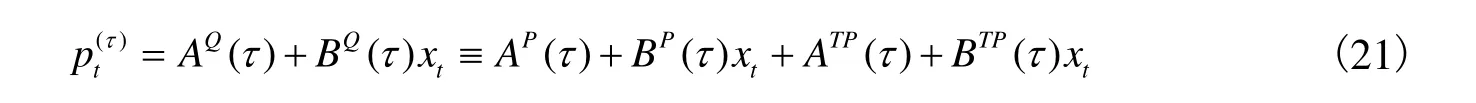
仿射矩阵 AQ(τ )和 BQ(τ )可以分解为短期利率仿射矩阵 AP(τ )、BP(τ )和期限溢价仿射矩阵 ATP(τ )、BTP(τ )两部分。

惩罚项的引入可以稳定似然函数值并且简化全局最优的搜寻过程，主要防止局部最优影响似然函数全局最优化。该项中 σp作为调整系数，决定似然函数初始值，影响似然函数极大值搜寻的速度。Bikbov 和Chernov(2010)在其文章中将该值设置为300，本文参考该值的设定，主要目的是简化最优化值搜索过程，使得估计结果快速接近或达到全局最优。

在对模型的优化过程中，本文使用单纯形法和高斯牛顿法求解全局最优。在参数初始值的获取上，本文采用了两种方法，一种通过使用一阶向量自回归法AR(1)得到参数初始点，另一种则由Sobol 伪随机数列生成初始点序列，通过对序列元素逐个计算比较似然函数值。在实际优化过程中，Sobol 数列的方法在计算结果上优于AR(1)，但同时伴随着的过多初始点所带来的庞大的计算量，该方法也耗时较长。

本文使用Matlab7.0 实现模型构建和估计。表1 和表2 为状态转移矩阵 Φx和波动矩阵的参数估计值，括号内为优化过程中似然函数极大值点的Hessen 矩阵求得参数标准误。状态转移矩阵 Φx特征值的模小于1，模型估计的参数是稳定的。从参数估计结果可以看出，CPI 变化率与景气指数自身相关性较低，除受自身影响外，受短期利率影响较多。短期利率则呈现较高的序列自相关，自相关系数为0.973,4。受其他因素影响并不显著。表2 中3 个隐因子的自相关程度都较高，隐因子3 对隐因子1 和2 的影响较多。

表3 为市场风险价格矩阵系数，参照式(9)。LR 是条件为 λ1f= 0的似然比检验值，其分布为渐近3 阶卡方分布 χ2(3)。中括号内为检验中对应的P 值。从检验结果可以得出，宏观因素通过 λ1f矩阵对风险价格施加的影响是显著的，本文后续将对宏观因素的影响程度进行进一步分析。

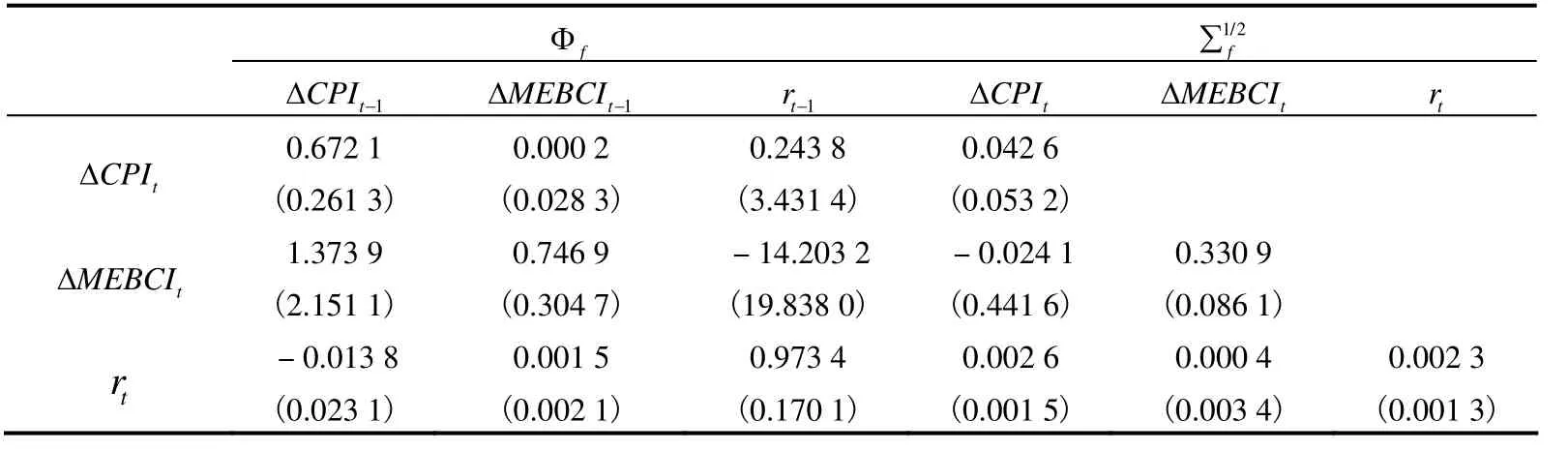
表1 宏观因子参数估计值

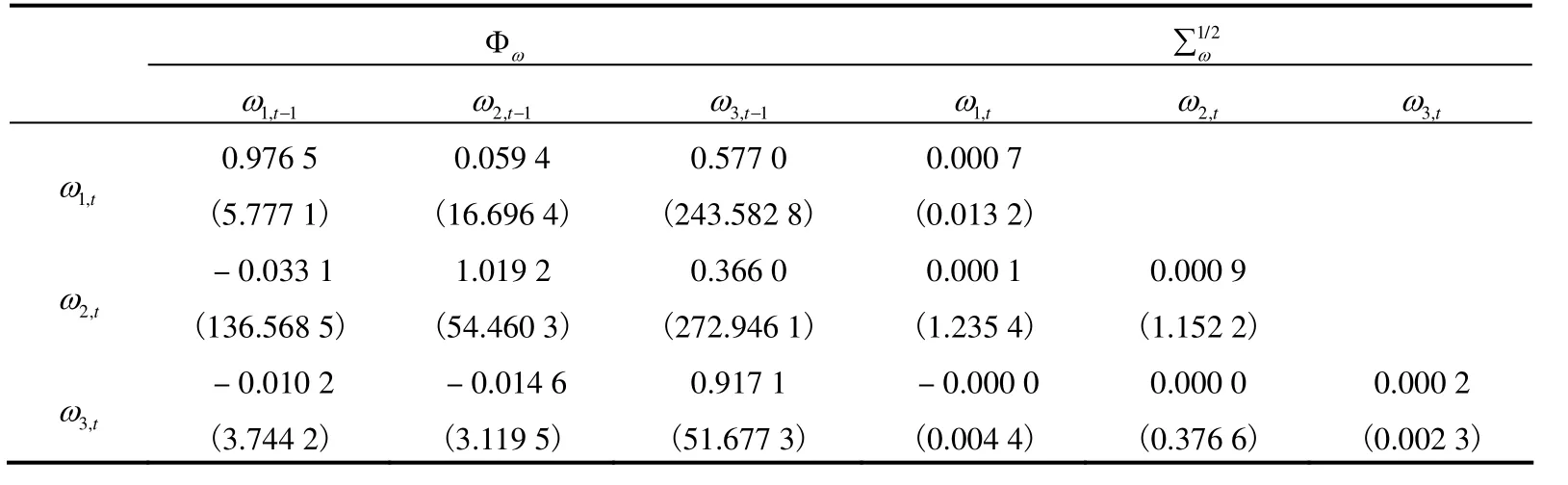
表2 隐因子参数估计值

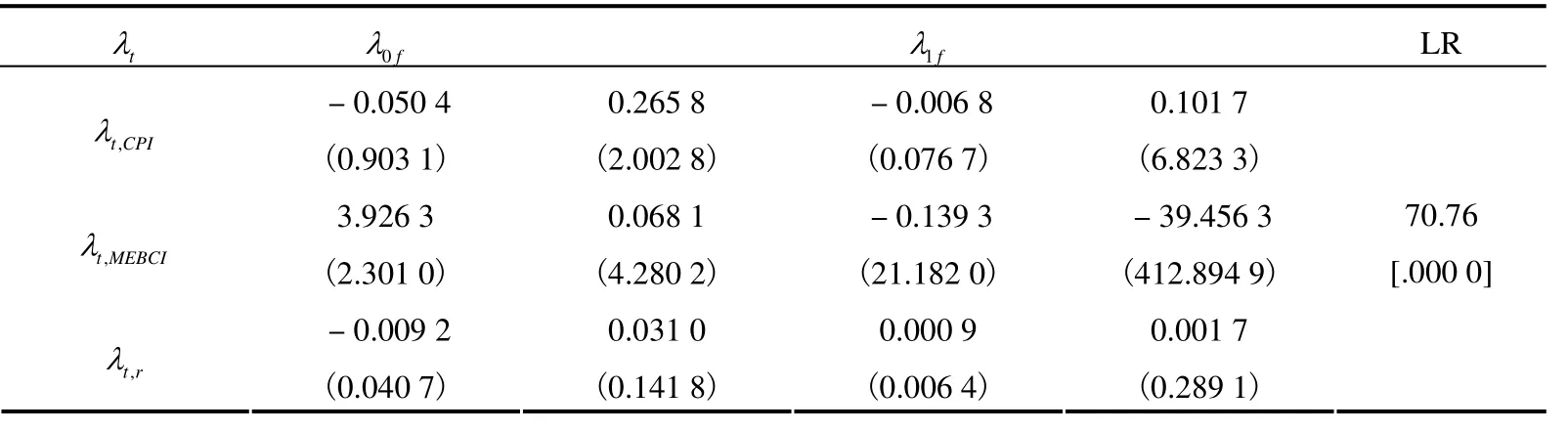
表3 市场风险价格参数估计值

图1 为三种期限国债收益率模型预测和拟合结果。预测值为卡尔曼滤波预测输出结果，拟合值则为模型拟合结果。图1 中可以直观看出，模型拟合的效果较好，而预测收益率数据较实际数据具有一定的滞后性，反映预期存在一定的粘性。其拟合和模型预测误差的统计如表4。SDME(Standard Deviation of Measurement Error)表示模型测量误差的标准差，各期限国债收益率测量误差均保持在5 个基点内。各期限国债的预测误差的标准差SDFE(Standard Deviation of One-month-ahead Forecasts Error)分布较为均匀，都保持在20 个基点左右。期限为1 月的短期利率tr，其预测误差相对其他期限国债较高，为35.63 个基点。这和模型估计过程中设定短期利率拟合误差为0 的方法有关，但这一做法可以更加准确的估计月度期限溢价值。

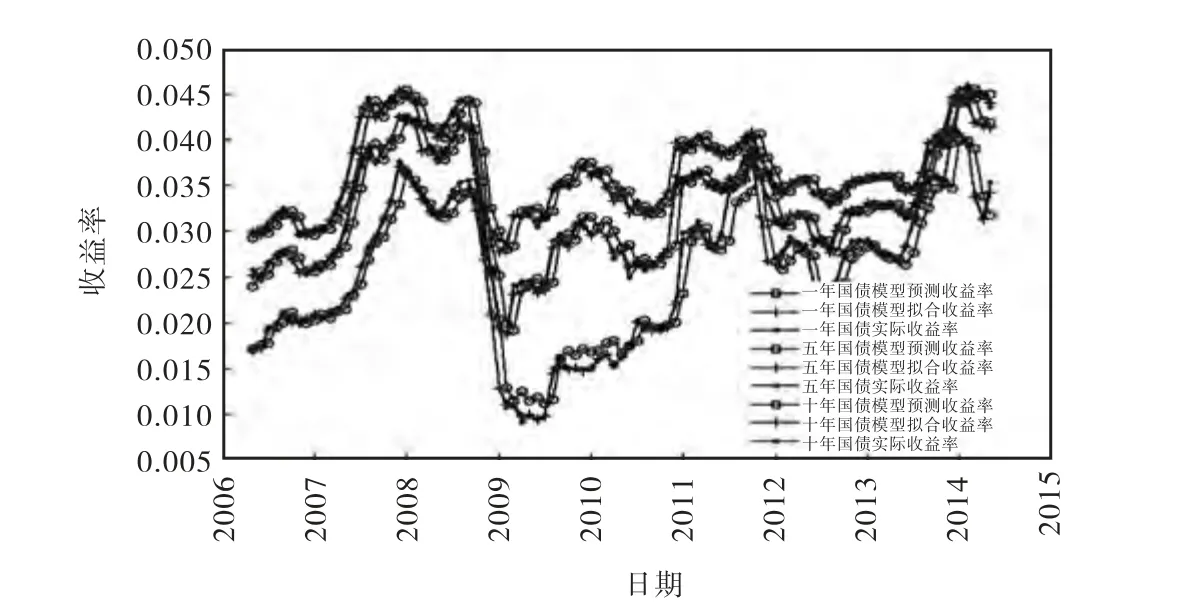
图1 国债预测、拟合和实际收益率时间序列图

表4 模型测量误差标准差和预测误差标准差

四、期限溢价静态和动态特征分析

1. 期限溢价静态分析

根据式(18)定义，期限溢价和超额收益的时间序列如图2 所示。从期限溢价的时序图可以看出，多数情况下，市场对于未来不确定性风险的补偿为正值，而2009 年初至2010 年初的时间段内，出现了样本期内唯一的长时间负值的情况。本文认为，这主要由市场对未来经济政策预期所决定。具体来看，2007 年下半年至2009 年初，次贷危机和世界性金融危机使得我国经济增速出现大幅度下滑，市场预期投资者将抛售风险资产而持有无风险资产进行避险，国债价格也随预期而上升。在对经济走势预期的同时，市场对政策调控的预期也会随着经济持续低迷而逐步强化。部分投资者预期认为，持有国债可能会导致潜在的资本损失(刺激政策推出会导致无风险资产价格上升走势出现变化)，这种对政策预期的不确定性会随着经济持续低迷而加剧，市场所要求的溢价补偿也会随之上升。随后，2009 年初大规模刺激政策的实施使得市场预期出现反转，投资者之前对于无风险资产价格下跌的忧虑逐渐成为市场的一致预期，期限溢价水平也大幅下降。从图3 可以看到，伴随宽松财政政策的持续，期限溢价长期呈现负向变动趋势。到2010 年初，固定资产投资、CPI 大幅上升，经济出现过热现象。央行于2010 年上半年3 次提高了存款准备金率，政策出现收紧的态势，期限溢价也随着政策预期调整向正值变动。

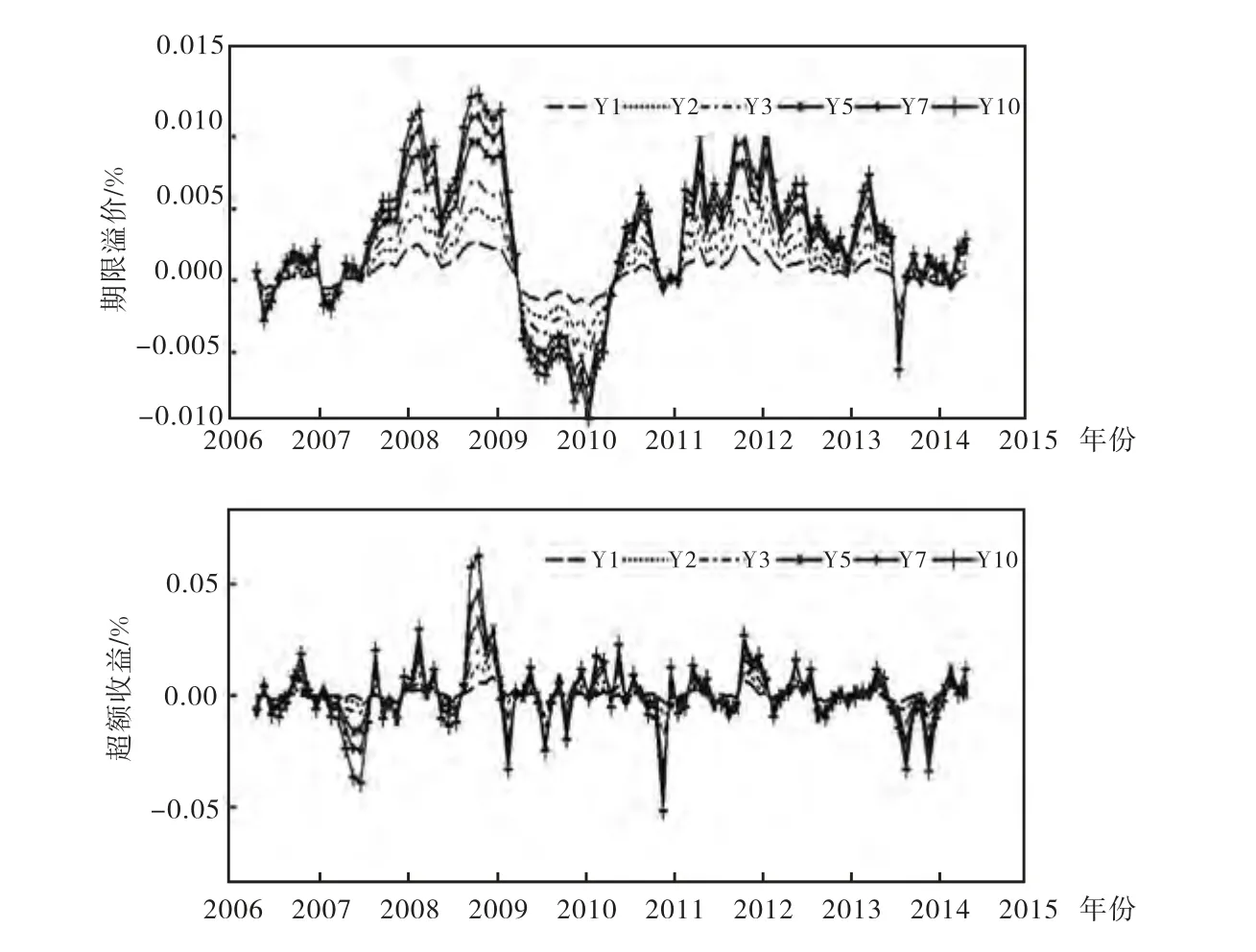
图2 一月期国债期限溢价和超额收益时间序列图

相较期限溢价，超额收益波动幅值和频率均高于前者。由图2 中可视10 年期国债一月期超额收益水平在正负6 个基点(年化为正负72 个基点)的范围内波动。表5 中，超额收益均值呈现出先增后减的分布。1 年期至5 年期的超额收益保持正向增长，5 年期国债超额收益均值达到5.24 个基点。7 年期和10 年期国债均值则呈下降态势，10年期均值水平甚至小于1 年期收益均值水平，这与期限溢价均值随期限正向增大的特征产生了明显的差异。表5 第五行所示，根据式(19)测算，期限溢价在超额收益中所占比重随期限增大而逐渐下降，表明期限越长的债券其超额收益受市场预期影响越小，而当期冲击的影响效果越突出。这从一个层面反映了我国长期国债市场缺乏市场预期，多数机构投资者以资产配置的目的持有到期，导致价格受市场预期影响的敏感性偏低。而从期限溢价和超额收益相关性分析结果也说明这一点，两者的相关程度随期限增大有所下降，期限溢价和超额收益一年期至十年期溢价相关性从0.395,9 到0.324,0 不等。这与Kim 和Wright(2005)实证研究美国数据中，超额收益与期限溢价存在0.83 的相关度的结果存在较大的差距。这反映了我国市场整体预期能力偏弱。我们认为，这主要因为我国“政策市”特征以及货币政策注重直接性功能调节，而在市场预期层面缺乏引导所致。这种市场特征促成了期限溢价与超额收益之间的较大差异。

对表5 统计结果进行总结可以得出，我国国债市场整体对于系统性风险的预期不足，各期限国债溢价的预期特征存在较大差异，短期国债期限溢价的预期属性表现强于中长期国债。在预期成分中，表5 所示模型宏观因子的解释比重能够达到55.33%～60.74%,，这说明通胀、经济活动以及货币政策的波动对于期限溢价变动具有显著的影响。

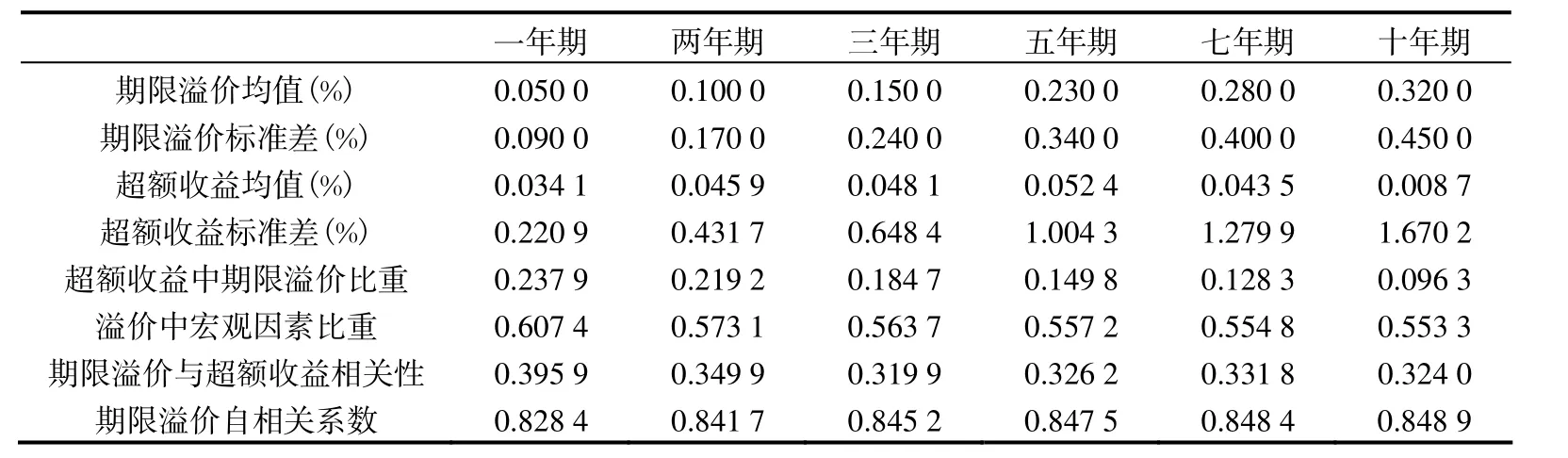
表5 期限溢价与超额收益的统计特征分析

2. 期限溢价动态分析

为了进一步了解期限溢价受模型因子影响的特征，本文根据模型估计卡尔曼滤波所得的风险中性下的状态转移矩阵、因子冲击参数矩阵和期限溢价观测矩阵，构建面向期限溢价波动的状态空间模型，考察模型因子对市场溢价影响的动态效应。

式(22)中，xt为t 时刻模型因子，ux为模型因子冲击，yt为由t-1 时刻状态变量估计的期限溢价。本部分使用Matlab7.0 Simulink 模块实现。

图3 为一年期国债期限溢价脉冲响应时序图，第一行为期限溢价分别在CPI 变化率、宏观经济景气指数变化率以及短期利率0 时刻冲击下的响应时序。第二行为3 种隐因子0 时刻冲击下的期限溢价脉冲响应时序。

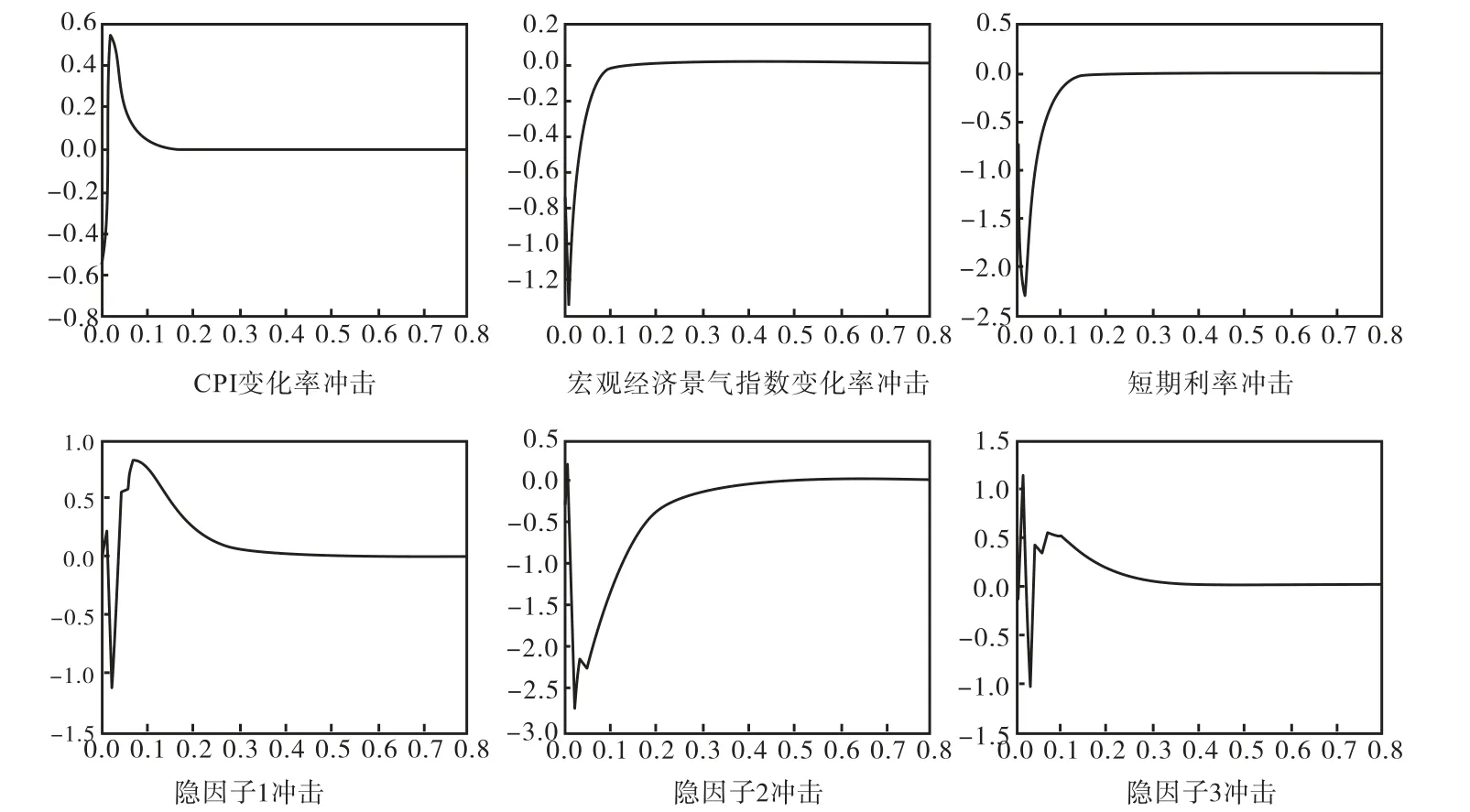
图3 一年期国债期限溢价脉冲响应时序图

整体来看，模型因子冲击下市场期限溢价出现短暂偏离均衡水平的现象。冲击前，溢价长期处于均衡水平，各模型因子保持不变，市场对于因子的预期不存在差异。冲击发生后，投资者对于未来变动预期出现分化，部分投资者认为冲击会持续，而另一部分投资者则持相反态度，市场预期的不确定性随之增大，期限溢价偏离均衡水平。随着时间推移，模型因子值回复到冲击前水平且长时期不变，投资者预期逐渐调整而趋于一致，预期的不确定性下降使得期限溢价回复到均衡水平。

从具体模型因子来看，CPI 变化率正向冲击使得期限溢价出现先减后增的变动态势。我们认为债券类资产对于通胀具有较高的敏感度，价格在通胀冲击下会出现超调。在CPI 变化率冲击下，市场名义收益率伴随通胀水平上升而快速提高，在这个过程中，资产价格下降和通胀持续上升的市场预期使得期限溢价快速下滑。随后，通胀水平趋于稳定，市场预期不确定性逐渐下降，过度调整的债券价格将根据预期调整而上升，期限溢价也逐渐由正值回复到均衡水平。相比通胀风险，期限溢价在景气指数变化率和短期利率正向冲击下则表现为负向变动。景气指数方面，当经济加速增长既表现为景气指数上涨时，部分投资者预期短期风险资产价格上升，从而倾向于持有短期资产放弃长期资产，购入高风险资产而抛售低风险资产(国债)。市场预期资金从国债市场流出，致使各期限国债溢价出现负向变动且溢价水平差距加大。货币政策方面，短期利率作为政策的代理变量，利率水平直接反映了市场流动性宽松或紧缩程度。短期利率上升使得部分市场主体预期未来债券价格下降，持有国债可能导致潜在的资本损失，市场期限溢价因此出现负向变动。从图2 中2013 年6 月份银行间市场流动性危机期间期限溢价走势可以看到这一特征。

隐因子方面，隐因子1 和隐因子3 冲击使得期限溢价表现震荡特征，隐因子2 则主要为负向变动。对于隐因子分析，Duffee(2008)在其研究中认为模型隐因子作为利率预期因素，与实际经济活动的波动相关。本文借鉴Bikbov 和Chernov(2010)、Chernov 和Mueller(2012)的方法，通过对隐因子与宏观经济因素进行大量相关分析识别潜在宏观经济信息和政策冲击。本文排除CPI 和宏观经济景气指数编制中直接涉及的宏观变量，选取包括信用利差、国债流动性、货币供应量、对外贸易、财政、外汇、固定资产投资、房地产等多方面宏观金融和经济变量，部分变量经过X12 季度调整。分析之前，本文首先进行隐因子主成分分解，提取隐因子主要特征序列。表6 为隐因子主成分分解后的三个主成分。从表6 中可知，前两个主成分能够解释85%,以上变动，其中第一主成分解释比重较高，对于隐因子波动的解释力达到49%,。

表6 隐因子主成分分析

本文对隐因子和主成分经济含义进行分析。在对众多宏观变量分析后发现隐因子2 与贸易出口价格指数具有-0.7 的相关性，主成分1 与出口价格指数存在-0.64 相关性，其时间序列如图4。隐因子3 与国房景气指数变化率具有0.51 的相关性，但主成分序列与国房景气指数相关性并不高。隐因子1 与上文宏观指标相关程度均较低。本文分析认为，对外出口是我国宏观经济风险的重要影响因素之一。宏观经济景气指数编制指标中并不包含对外出口指标，这可能是隐因子与其相关性较高的主要原因(风险价格参见公式9)。隐因子2 隐含房地产景气信息，可能是因为房地产对短期利率(货币政策)敏感度较高，部分反映了货币政策调控所带来的宏观经济风险。

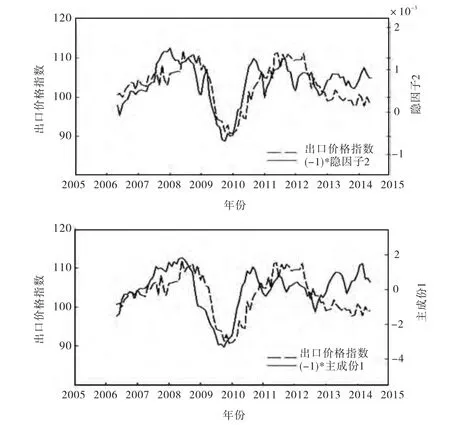
图4 宏观变量与隐因子时间序列图

由上述分析推断，除模型3 种宏观因子外，对外贸易情况可能是影响期限溢价形成和波动的另一个重要的宏观因素。我们认为这主要与我国依赖于对外贸易和投资拉动的经济增长结构有关。而经济增长的另一个拉动力固定资产投资(全社会固定资产投资指标)，由于与宏观经济景气指数编制中的工业投资指标具有较大的关联性，所以隐因子内含的该信息较少。

综合上述实证分析发现，除CPI、宏观经济景气指数以及短期利率对期限溢价具有较大影响外，出口价格指数也可能是影响期限溢价波动的重要因素，宏观经济波动对于市场期限溢价水平具有显著的影响。从期限溢价波动特征来看，期限溢价在冲击结束后均能回复到原有水平，表明在一定市场和经济条件下，溢价具有均衡值。我们认为，期限溢价形成和波动主要源于市场预期调整以及对于未来经济政策判断的不确定性，溢价水平表征了预期的不确定性程度。

同时，期限溢价作为超额收益的预期，其与超额收益的较大偏差从一个侧面反映出我国市场对于宏观风险预期能力不足。从市场效率来看，我国市场信息流动不顺畅，信息分布不对称以及获取信息的成本较高都是市场有效预期形成与快速调整的障碍，市场预期表现出粘性特征。从政策方面来看，我国货币政策实施缺乏指引，市场对于政策预期的不确定性偏大，货币政策实施过程表现出了脉冲冲击的特征。在这种情况下，市场预期调整更多的表现为事后调整，这就会加剧市场的波动，削弱市场风险预期能力。总之，稳定市场预期和进行合理的引导是减少市场波动，提升政策调控效率的重要的途径。加强信息流动和降低信息分布的不对称可以进一步提升市场期限溢价对于超额收益的预期能力，这对政策制定者和投资者都具有重要意义。

五、本文结论

本文通过构建6 因素无套利宏观金融模型，对银行间市场国债期限溢价和超额收益进行估计。在对期限溢价的静态特征分析中发现，期限溢价与超额收益在幅值方面存在较大差异，并且预期解释比重随期限增大而逐步下降。从波动关系来看，两者相关系数较低，表明市场对于未来超额收益的预期能力偏弱。随后，本文在估计所得模型系数的基础上，构建状态空间模型，对市场期限溢价动态特征进行分析。结果发现，CPI变化率、宏观经济景气指数变化率、短期利率均能对市场期限溢价产生显著的影响，但长期内并不能使期限溢价水平发生变化。在对隐因子与宏观因素相关分析中发现，出口贸易价格指数可能是影响期限溢价波动的潜在原因。

贯穿全文，本文基于预期理论，对期限溢价形成和波动的机理提出了一个新的解释。本文认为期限溢价源于市场对于未来风险不确定性的补偿，而经济和政策的冲击只会对期限溢价造成短暂影响，并不会使溢价发生偏移。这主要由于随着外部环境条件变动，市场的预期会不断进行调整，远期收益率中的预期值和期限溢价值也会随之趋于稳定，期限溢价最终达到与市场对未来风险预期的不确定程度相匹配的数值水平。

本文认为，期限溢价所表征的预期属性是宏观政策调整和投资者决策的重要依据。从宏观决策来讲，期限溢价稳定有助于提高政策调控效率和精确性，并且可以有效地发挥市场预期的自我调整能力。从微观投资者来讲，稳定合理的期限溢价有助于减少市场投机，引导投资者合理投资，提升市场资金配置的效率。鉴于此，本文提出以下建议：第一，宏观调控应注重加强政策指引，减少政策冲击，降低市场政策预期中的不确定性。尤其增强货币政策的前瞻性引导，促使市场形成合理预期并实现自身的有序渐进调整。第二，丰富市场主体结构，提升市场信息效率。允许更多类型机构投资者进入银行间市场进行交易，丰富债券持有偏好，提升国债利率的政策指引作用；扩展信息流通渠道，降低由于信息不对称导致的预期的异质性差异，使得债券价格处于合理均衡水平；加强信息监督，严惩虚假恶意的市场信息，减少不必要的价格波动。第三，加强对银行间市场投资者的教育，通过培训等手段缩小投资者之间的禀赋差异，提升投资者市场判断和政策解读能力，更好的服务于货币政策调控。总之，减少市场不必要的波动并降低市场预期的不确定性，是提升市场配置效率和政策调控效率的重要途径。我国银行间市场无论从规模或结构都处于快速发展完善的阶段，在实现“硬件”加速建设的同时，做好“软实力”的培养更是市场良性发展的重要前提。

［1］ 陈守东等. 利率期限结构与宏观经济——基于动态潜在因子模型的研究[J]. 吉林大学社会科学学报，2014(2)：52-61.

［2］ 何晓群，王彦飞. 中国利率期限结构与宏观经济运行的关系——基于动态Nelson-Siegel 模型的研究[J]. 经济理论与经济管理，2014(8)：69-77.

［3］ 金雯雯等. 利率期限结构内含的宏观经济信息——基于TVP-VAR 模型的时变参数研究[J].经济评论，2014(5)：123-135.

［4］ 康 书，王志强. 中国国债利率期限结构的风险特征及其内含信息研究[J]. 世界经济，2010(7)：121-143.

［5］ 石柱鲜，孙 皓，邓 创. 中国主要宏观经济变量与利率期限结构的关系：基于VARATSM 模型的分析[J]. 世界经济，2008(3)：53-59.

［6］ 孙 皓，石柱鲜. 中国的货币政策与利率期限结构：基于宏观——金融模型的研究途径. 经济科学，2011(1)：49-59.

［7］ 王安兴，余文龙. 收益率曲线预测国债风险溢价研究[J]. 中国管理科学，2012(20)：417-423.

［8］ 王志强，熊海芳. 结构变点、时变期限溢价与预期假说[J]. 数量经济技术经济研究，2012(5)：104-120.

［9］ 吴 丹，谢 赤. 中国银行间国债利率期限结构的预期理论检验[J]. 管理学报，2005(5)：536-541.

［10］ 谢 赤，陈 晖，何 源. 基于理性期望的利率期限结构预期理论与期限溢酬[J]. 系统管理学报，2008(3)：283-289.

［11］ 徐小华. 中国国债利率期限结构的风险值研究[J]. 世界经济，2007(6)：56-63.

［12］ 余文龙，王安兴. 中国货币市场利率的期限溢价[J]. 证券市场导报，2010(9)：34-40.

［13］ 余文龙，王安兴. 基于动态Nelson-Siegel 模型的国债管理策略分析[J]. 经济学季刊，2010(4)：1403-1426.

［14］ 郑振龙，吴颖玲. 中国利率期限溢酬：后验信息法和先验信息法[J]. 金融研究，2009(10)：68-82.

［15］ 郑振龙，柯 鸿，莫天瑜. 利率仿射模型下的利率风险价格形式实证研究[J]. 管理科学学报，2010(13)：4-15.

［16］ 朱世武，陈健恒. 利率期现结构理论实证检验与期限风险溢价研究[J]. 金融研究，2004(5)：78-99.

［17］ 朱 波，文兴易. 利率期限结构宏观金融模型研究新进展[J]. 经济学动态，2011(7)：101-105.

［18］ Ang A.，Piazzesi M. A No-arbitrage Vector Autoregression of Term Structure Dynamics with Macroeconomic and Latent Variables [J]. Journal of Monetary Economics，2003(50)：745-87.

［19］ Ang A.，Bekaert G.，Wei M. The Term Structure of Real Rates and Expected Inflation [J]. The Journal of Finance，2008(2)：797-849.

［20］ Bikbov R.，Chernov M. No-arbitrage Macroeconomic Determinants of the Yield Curve [J]. Journal of Econometrics，2010(159)：166-82.

［21］ Campbell J. Y.，Cochrane，J. By Force of Habit：A Consumption-Based Explanation of Aggregate Stock Market Behavior [J]. Journal of Political Economy，1999(107)：205-51.

［22］ Cochrane J. H.，Piassesi M. Bond Risk Premia[J]. The American Economic Review，2005(1)：138-60.

［23］ Cochrane J. H.，Piassesi M. Decomposing the Yield Curve [R]. Chicago Booth Working Paper，2009.

［24］ Chernov M.，Mueller P. The Term Structure of Inflation Expectations [J]. Journal of Financial Economics，2012(106)：367-94.

［25］ Dai Q，Singleton K. J. Specification Analysis of Affine Term Structure Models [J]. Journal of Finance，2000(5)：1943-78.

［26］ Dai Q，Singleton K. J. Expectation Puzzles，Time-varying Risk Premia，and Affine Models of the Term Structure [J]. Journal of Financial Economics，2002(63)：415-41.

［27］ Duffee G. R. Term Premia and Interest Rate Forecasts in Affine Models [J]. Journal of Finance，2002(57)：405-43.

［28］ Duffee G. R.，Stanton R. H. Estimation of Dynamic Term Structure Models [J]. Quarterly Journal of Finance，2012(2).

［29］ Fama，E. F.，Bliss，R. R. The Information in Long-Maturity Forward Rates [J]. The American Economic Review，1987(77)：680-92.

［30］ Kempf A.，Kron O.，Uhrig-Homburg M. The Term Structure of Illiquidity Premia [J]. Journal of Banking & Finance，2012(36)：1381-91.

［31］ Kim，Don H.，Jonathan H. Wright. An Arbitrage-Free Three-Factor Term Structure Model and the Recent Behavior of Long-Term Yields and Distant-Horizon Forward Rates [J]. Finance and Economics Discussion Series，2005，33.

［32］ Liu J.，Longstaff F. A.，Mandell R. The Market Price of Risk in Interest Rate Swaps：The Roles of Default and Liquidity Risks [J]. Journal of Business，2006(79)：2337-60.

［33］ Ludvigson S. C.，Ng S. Macro Factors in Bond Risk Premia [J]. The Review of Financial Studies，2009(12)：5027-66.

［34］ Nelson C.，Siegel A. Parsimonious Modeling of Yield Curves [J]. Journal of Business，1987(60)：473-98.

［35］ Piazzesi M.，Schneider M. Equilibrium Yield Curves [J]. NBER Macroeconomics Annual，2006(21)：389-472.

［36］ Piazzesi M.，Salomao J.，Schneider M. Trend and Cycle in Bond Premia [R]. Stanford Working Paper，2013.

［37］ Wright J. H. Term Premia and Inflation Uncertainty：Empirical Evidence from an International Panel Dataset [J]. The American Economic Review，2011(101)：1514-34.