关于根与底座的几点注记

王正萍，刘 洋，许庆兵

（1.滁州职业技术学院督导室，安徽滁州239000；2.滁州学院数学系，安徽滁州239000）

在环论的发展历史上，学者们很早就得出：在每个有限维代数A中，存在一个双边的理想B，使得A/B是半单的。这就为A的研究提供了三个着手点：利用半单代数的理论对A/B的研究；对幂零理想B的研究；对A与A/B关系的研究。一个自然的问题是A/B的性质是否可以提升到A上来。由于上述方法为代数研究带来了丰硕的成果，从而在对任意环与模的研究过程中，人们也希望有一个与B相当的对象可以利用，这就引出了根与底座的概念，这一概念现在已成为代数学的重要概念及工具之一。

1 根与底座的等价定义

根与底座的概念有多种形式，这些形式都是等价的，为了方便介绍这些概念，首先介绍极大子模、极小子模、大子模与小子模等概念。更多相关的一些知识可以参见文献［1-5］。

M的一个子模A称为极大子模（极小子模）当且仅当对任意B⊆M，B真包含于A，则B=M（对任意B⊆M，B 真包含于 A，则 B=0）。

M的一个子模A称为在M的小子模（亦称为多余子模，记为A＜＜M），若对任意U⊆M，A+U=M，则U=M。M的一个子模A称为在M的大子模（亦称为本质子模，记为A◁M）），若对任意U⊆M，A∩U=0，则U=0。设U是R模类，M是左R模Im h称为U在M中的迹（trace），Re j（M，U）称为U在M中的余迹（reject）。

定义1 设K是M的小子模，则M的小子模的和称为M的根，记为

定义2 设L是M的极大子模，则M的极大子模的交称为M的根，记为

事实上，这三个定义是等价的，下面给出证明。

证明 定义1⇒定义2

定义2⇒定义3

设L在M中极大，vL：M→M/L是到单模M/L上的自然满同态，则Ker（vL）=L，因而有Re j（M，N）⊂

定义3⇒定义1

对任意同态 h：M→N，若 K=M，由文献［1］5.1.3（c），h（K）=N，若 N 半单，则 0是 N 的惟一小子模，所以h（K）=0，即K⊂Ker（h），因而定义3蕴含定义1。

底座是根的对偶概念，下面给出底座的几个等价定义。

定义4 设K是M的小子模，则M的小子模的交称为M的底座，记为

定义5 设L是M的极大子模，则M的极大子模的和称为M的底座，记为

证明 定义4⇒定义5

设L是M的单子模且K◁M，则K∩L≠0⇒K∩L=L⇒K⊂L，所以定义4蕴含定义5

定义5⇒定义6

由于一个半单模的同态像仍为半单模，对半单模的和也有这样的结果，所以Tr（M，N）必是M的一个半单子模，即M是单子模的和，因此是M的一切单子模的和。

定义6⇒定义4

下面给出根与底座的一些常见的性质，关于这些性质的证明可以参见文献［1-2］。

性质1对R模M有：

（1）对任意态射 f：M→N，有：

1）f（Rad（M））⊆Rad（N）；

2）Rad（M/Rad（M））=0；

3）若Ker f⊆Rad（M），则f（Rad（M））=Rad（f（M））。

（2）Rad（M）是M的一个自同态子模。

（3）若M的每个真子模包含在一个极大子模中，则Rad（M）=M。

（4）M有限生成当且仅当Rad（M）=M且M/Rad（M）是有限生成。

（5）若 M=⊕ΛMλ，则 Rad（M）=⊕ΛRad（Mλ），且 M/Rad（M）≅⊕ΛMλ/Rad（Mλ）。

（6）若M有限余生成且Rad（M）=0，则M半单且有限生成。

性质2对R模M有：

（1）对任意态射f：M→N，有（fSoc（M））⊆Soc（N）。

（2）对 K⊆M，有 So c（K）=K∩Soc（M）。

（3）Soc（M）◁M 当且仅当对每个子模 K⊆M，Soc（K）≠0。

（4）Soc（M）是M的自同态子模。

（5）Soc（⊕ΛMλ）=⊕ΛSoc（Mλ）。

模n剩余类环Zn是一类常见而又重要的环，下面给出其底座的计算方法。

例 1 计算 Zn的根 Rad（Zn）。

例2 计算Zn的底座Soc（Zn）。

注 （1）对 Z/p1…pkZ，Rad（Z/p1…pkZ）=0，Soc（Z/p1…pkZ）=Z/p1…pkZ。

（2）对 Z/pnZ，Rad（Z/pnZ）=pZ/pnZ≅Z/pn-1Z，Soc（Z/pnZ）=pn-1Z/pnZ≅Z/pZ。

（3）对整环 Z，Rad（ZZ）=Soc（ZZ）=0，Rad（QZ）=Q，Soc（QZ）=0，Rad（QQ）=0，Soc（QQ）=Q。

2 广义矩阵环的Jacobson根

在根的定义中，把 M 改为 RR或RR，则 Rad（RR）=Rad（RR）称为 R 的 Jacobson 根，记为 J（R），由此可见Jacobson根是模M根的特殊形式，这类根在环论和代数表示论中均有着广泛的应用［6-12］。

R中的元素r称为左（右）拟正则，若存在t∈R，使得r+t-tr=0（r+t-rt=0），元素r称为拟正则的，若其既是左拟正则又是右拟正则。在有单位元的环中，式子r+t-tr=0等价于方程（1-t）（1-r）=0，因此在这类环中元素r是左拟正则的当且仅当（1-r）左可逆，对右正则元也有类似的结论，因而对环R的左（右）理想I，若I⊆R，且I拟左（右）正则当且仅当对任意x∈I，1-x左（右）可逆。事实上这个结果是著名的Nakayama引理的一部分，下面用这个结论来研究广义矩阵环的Jacobson根。

对形式三角矩阵环作进一步的扩张，使其具有如下形式

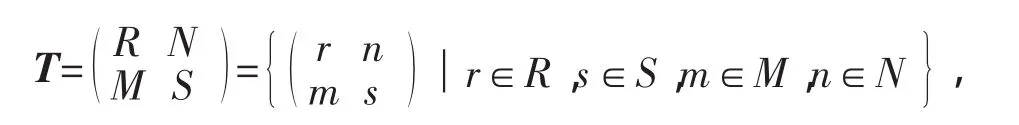
其中，R、S是有单位的结合环，M是左S-，右R-双模，N是左R-，右S-双模，φ：N⊗SM→R是双R-同态，ψ：M⊗RN→S 是双 S-同态，且满足 φ（n⊗m）n'=nψ（m⊗n'），ψ（m⊗n）m'=mφ（n⊗m'），这里 m，m'∈M，n，n'∈N。T上定义的加法为普通矩阵的加法，其乘法定义为则T对于所定义的运算作成环，这个环就是广义矩阵环，也称为Morita系统环，由定义可见形式三角矩阵环是此类环的一种特例［11］。

［1］KASCHF.Modulesand Rings:Atranslation fromthe German“Moduln und Ringe”（London Mathematical Society Monographs）［M］.London:Academic Press,1982.

［2］WISBAUERR.Foundations of Module and Ring Theory［M］.Philadelphia:Gordon Breach Sience Publishers,1991.

［3］GARDNERBJ,WIEGANDTR.Radical theory of rings［M］.New York:Marcel Dekker Inc.,2004.

［4］ANDERSONFW,FULLERK R.Rings and categoriesof modules［M］.2nd ed.New York:Springer,1992.

［5］LAMTY.A First Coursein Noncommutative Rings［M］.New York:Springer-Verlag,1991.

［6］SANDSA D.Radicals and Morita contexts［J］.JAlgebra,1973,24:335-345.

［7］SANDSA D.Radicals of structural matrix rings［J］.Quaest Math,1990,13:77-81.

［8］SNIDERRL.Complemented hereditary radicals［J］.Bull Austral Math Soc,1971,4:307-320.

［9］VANWL.Special radicalsin structural matrix rings［J］.Comm Alg,1988,16:421-435.

［10］VELDSMANS.On theradicalsof structural matrix rings［J］.Monatshefte Math,1996,122:227-238.

［11］KRYLOV PA,TUGANBAEV A A.Modules over formal matrix rings［J］.JMath Sci,2010,171（2）:248-295.

［12］VELDSMANS.Radicals of Moritaringsrevisited［J］.Bul Acad Stiine Repub Mold Mat,2007（2）:55-68.