基于增强的同质相似性和旋转不变性的MRI去噪

陈创泉，房少梅

（1.吉林大学珠海学院公共基础课教学与研究中心，广东珠海519041；2.华南农业大学数学与信息学院，广东广州510642）

在磁共振成像（Magnetic Resonance Imaging，MRI）图像获取过程中由于时间和技术上的限制，通常呈现出噪声伪影。去除这些噪声，同时保留MRI图像原本的边缘与细节特征，对图像分割、配准等均具有非常重要的意义［1-2］。

基于自然图像的冗余性和周期性的特点，非局部平均（NLM）滤波方法被提出［3］。这种方法被用于MRI图像并呈现出较好的结果，并尚有很大的改进空间［4-6］。近年来，Manjón等［7］提出了非局部平均（NLM）滤波方法的一种旋转不变性形式，据笔者掌握的文献所知，该方法是目前最优秀的MRI去噪算法之一。但是，该方法在计算权重的过程中忽略了块状的结构信息，例如边缘、血管、片状，为此，本文提出了一种基于增强的同质相似性和旋转不变性的三维非局部平均滤波方法，该方法的主要贡献在于：考虑到图像的旋转不变性和同质相似性，融合了体像素（voxel）的亮度、相应邻域块的均值、梯度以及一致锐度。通过这个融合，块状的结构信息，如边缘、角形、末端能被很好地保护。将所提出的方法和近年来相关的先进方法在Brainweb数据库进行定量对比，结果表明提出的方法均优于其他方法。最后，将提出的方法应用于OASIS临床数据库。

1 基于旋转不变性的3D非局部平均滤波算法

Manjón等［7］提出了一种基于旋转不变性测度的3D非局部平均滤波（PRI-NLM3D）算法。首先，噪声图像通过ODCT3D方法进行预处理，进而利用预处理后图像体像素的亮度及其均值计算相似度（权重），这些相似度（权重）被用于对原始的噪声图像进行去噪。具体的计算方法为

首先，使用ODCT3D方法对噪声图像u进行预处理，得到图像。式（1）中，Ωi表示搜索的范围，权重 β（i，j）由图像估计得出，最后应用于被观察的噪声图像u（i）表示图像中体像素i的亮度，是图像中以体像素i为中心的3×3×3块状Ni的亮度加权平均值，而h表示滤波参数。

2 基于同质相似性和旋转不变性的MRI去噪

2.1 旋转不变性测度和增强的同质相似性测度

Manjón等［7］利用体像素的亮度和相应邻域的均值作为相似性的测度。但是，从图1中可以看出这个简单的相似性测量没有充分考虑到同质性，因此导致了一个次优的结果。图1中，假设每一个邻域中心体像素的亮度是50，通过一个简单的计算可知，以i、j和k为中心的块具有相同的亮度平均值，即是50。因此，在滤波过程中，根据Manjón等［7］的算法，由体像素j和k产生的权重对参照体像素i的影响没有区别。但是，实际上体像素k应该被赋予一个更小的权重。

图1 PRI-NLM3D算法计算相似性

笔者使用一种新的相似测度来刻画这些相似块，即将平均梯度和区域相似测度（一致锐度）考虑进去（不单单是利用体像素的亮度和相应邻域块的均值作为相似性的测度）。平均梯度和区域相似性（一致锐度）都是属于旋转不变性测度，它们都能揭示相似块的不一致性，因此它们也是同质性测度。

2.1.1 平均梯度

梯度的离散化可以通过不同邻域结构的选择来实现其准确率和局部性。把Yu等［8］提出的2D平均梯度扩展到3D形式。令 AG2为当前体像素与最近6个不同方向体像素差异的平方值的和，即

其中，u（i）表示图像u中体像素i的亮度，ξi表示体像素i的3D空间邻域（包括当前体像素和包围着当前体像素的6个最近体像素，如图1所示），ξi表示ξi的基数（也就是ξi的体像素的数目）。图1中体像素i、j和k的平均梯度分别是0、2、10。平均梯度揭示了当前体像素和周围体像素的不一致性。

2.1.2 区域相似性（一致锐度）

将文献［9］提出的一致锐度的2D形式扩展到3D形式。假设Ni是以体像素i为中心、半径为r的局部邻域（相似块）。希望找到一个平面α将邻域Ni平分成两部分。首先，以体像素i为中心，建立空间坐标系。设过体像素i的平面α与平面XOY的夹角为θ1，而平面α与平面XOY的交线l和x轴的夹角为θ2（若平面 α 重合或平行于平面 XOY，则不考虑 θ2）。平面 α 将邻域 Ni平分成两部分 s1（i，r，θ1，θ2）和s2（i，r，θ1，θ2）。一致锐度用来评估邻域（相似块）的两个子集的差别，表示为

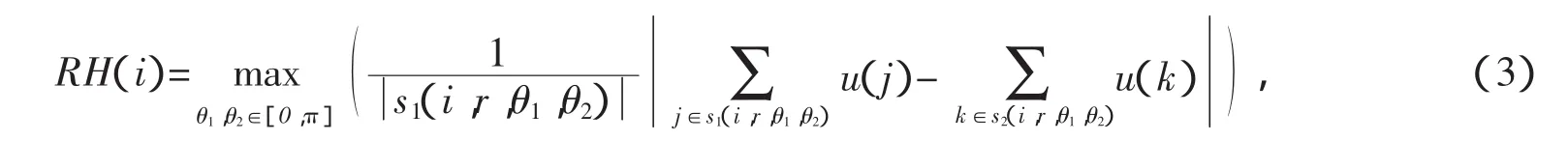
其中，u（j）表示图像u中体像素j的亮度，而s（1i，r，θ1，θ2） 表示s（1i，r，θ1，θ2）的基数（也就是s（1i，r，θ1，θ2）的体像素的数目）。笔者的定义和文献［9］的区别是加入了一个标准项（也就是1/s（1i，r，θ1，θ2）），因为RH（i）的计算是由不同尺寸大小的s（1i，r，θ1，θ2）计算得到的。

为了减轻一致锐度的计算复杂性，本文采取了图1的局部邻域（相似块）进行计算。另外，只有s（1i，r，θ1，θ2）=2的块被选择利用式（3） 进行计算。图1a、b、c中像素i、j和k的RH值分别是0、4和20。

2.2 权函数的选择

在非局部平均滤波中，权函数的选择对结果十分重要。传统的非局部平均滤波利用指数函数进行计算。Peter等［10］指出Geman-McClure（GM）函数能得到一个更好的下降行为，在光滑程度和边缘保护之间能得到更好的平衡。含参数H的光滑函数GMH的定义如下

其中，d表示块之间的距离，而参数H用于控制GM函数的下降程度。GM函数非常适用于非局部平均滤波的权重计算。与指数函数相比，当遇到非常不相似的块，GM函数不会使权重马上下降到0（如图2所示），这是使用GM函数的重要原因［10］。实验结果表明：GM函数相比指数函数能轻微增加滤波性能。

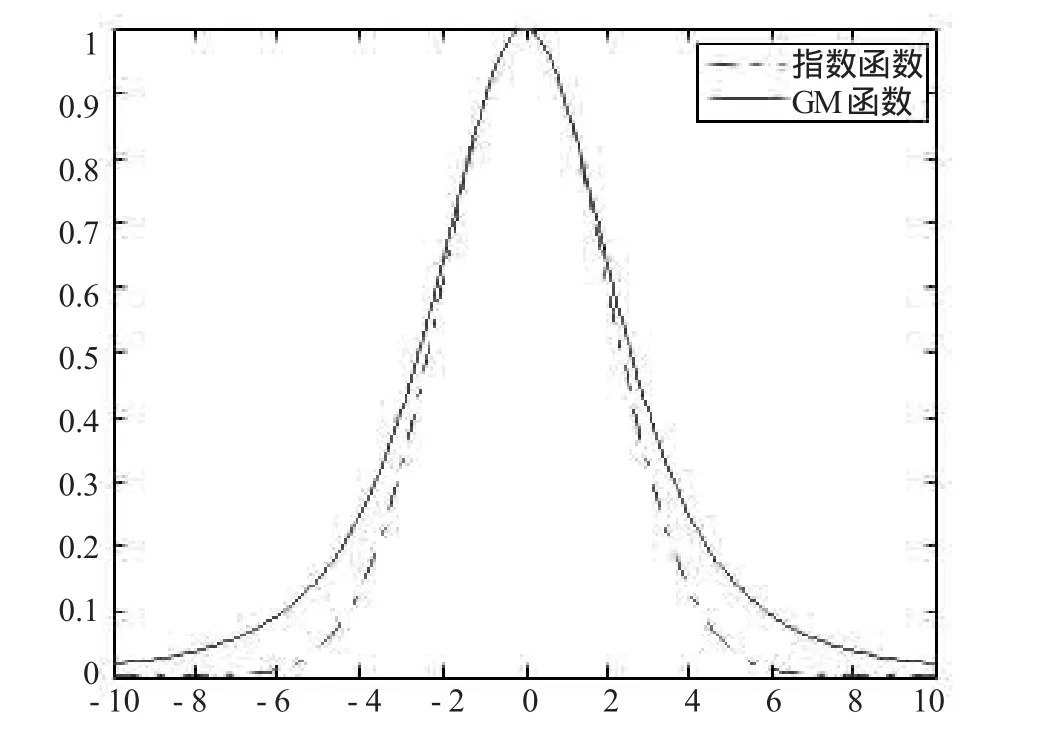
图2 指数函数和GM函数的对比

2.3 整合

像素预选方法是通过丢弃与当前体像素相似度较低的体像素来减少滤波的时间。本文使用Manjón［7］提出的预选方法，即只有预过滤后，与被参照块亮度平均值差别小于h的块状，才会对滤波过程产生贡献。将上述提出的修改加入PRI-NLM3D方法［7］，即其中，应用于噪声图像u的权重β（i，j）由ODCT3D方法预处理后的图像估计得到，Ωi表示搜索范围，（i）表示图像中体像素i的亮度表示图像中以体像 素 i为中心的3×3×3块状Ni的亮度加权平均值，h表示滤波参数，控制着平滑的强度（i）和（i）分别表示图像中体像素i的平均梯度和一致锐度。

把块状距离d分成d1、d2、d3三个部分。第1项d1利用块状的中心体像素，由于这个相似性测度是点细节而不是区域细节，因此它提供了一个对当前体像素较为精细的描述；第2项d2利用包围当前体像素的区域的均值，这个相似性具有较好的噪声免疫性以及具有丰富的图像特征。块状之间的距离由于不同的平均梯度，最终通过乘上惩罚系数T，目的是为了保护图像的边缘；第3项d3利用了包围当前体像素的区域的几何结构相似性（一致锐度），它能很好地保持图像的边缘、片状、血管等重要几何结构特征。实验中，w1=0.4，w2=0.5，w3=0.1（这个权重经过反复试验，证明是较优的参数）。笔者称这个方法为基于增强的同质相似性和旋转不变性的三维非局部平均滤波方法（PEHRI-NLM3D）。

为了达到去噪效果和计算时间的平衡，采取的搜索范围Ωi包含11×11×11个体像素［5］。增加搜索范围可能会轻微提高去噪效果，但同时又大大地增加了计算时间。由于相似测度是基于预处理后的图像实现的，因此将h的值设置为0.4σ，σ为噪声水平［7］。

2.4 针对莱斯噪声的校对

考虑到污染MRI图像的噪声为莱斯噪声，故采用Wiest-Daessle［11］提出的一种修正的方法，从而实现了无偏的去噪，即

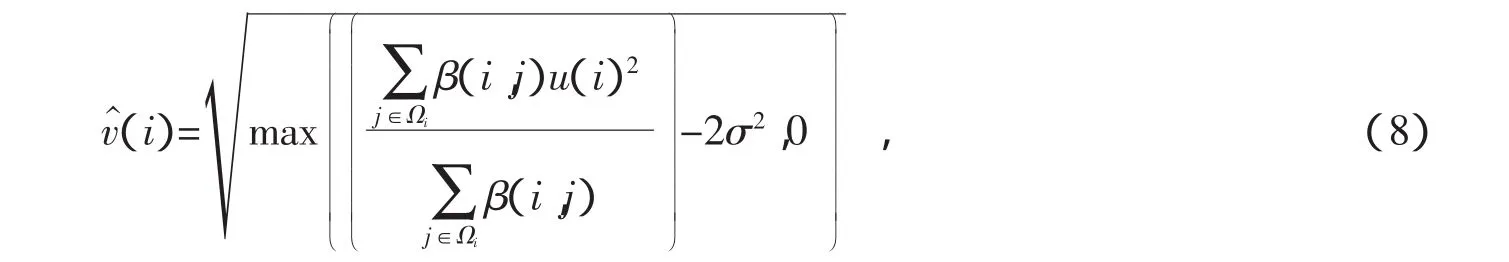
其中，σ表示标准差。将所提出的方法进行总结，如图3所示。

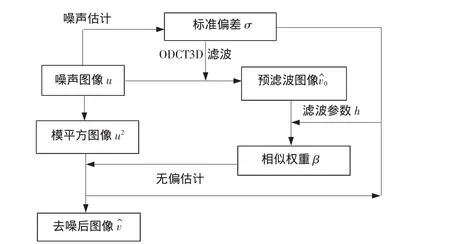
图3 本文提出的PEHRI-NLM3D滤波流程图

3 实验与分析

3.1 实验数据

利用麦吉尔大学（McGill University）研究机构的大脑图像数据库（http://www.bic.mni.mcgill.ca/ServicesBrainWeb/HomePage）提供的三种不同类型的MRI图像（T1w、T2w、PDw）来评估提出的算法。实验中，分别对测试图像添加2%～22%的莱斯噪声。将NL-means的不同实现方式：最优化的分块NLM滤波（Blockwise NLM）［5］、基于混合小波波段的 NLM 滤波（WSM）［6］、基于旋转不变性的 NLM 滤波（PRINLM3D）［7］、本文提出的基于同质相似性和旋转不变性的NLM滤波（PEHRI-NLM3D）进行比较。各方法使用了相应论文作者推荐的最优参数。峰值信噪比（PSNR）评价标准和结构相似性（MSSIM）［12］被用于评价各种方法的性能。所有的评价标准在头部组织进行计算［5-7］。

图4 PSNR和MSSIM实验结果比较

3.2 实验结果

图4提供了不同图像在不同噪声水平下的PSNR和MSSIM值。从图4可以看出：提出的PEHRINLM3D方法在所有情形下都是最优的方法，显著优于Blockwise NLM方法和WSM方法。和PRINLM3D方法相比，提出的PEHRI-NLM3D方法在中等的噪声水平下稍微优于PRI-NLM3D方法，但在高噪声水平下明显优于PRI-NLM3D方法。

图5提供了用不同算法滤波后的视觉比较。从视觉上可以看到：提出的PEHRI-NLM3D方法在成功去除噪声的同时可以很好地保护图像的细节纹理，使得同质的区域上出现更少的振荡。另外，图像残差绝对值图像没有显示出任何与解剖结构相关的信息。

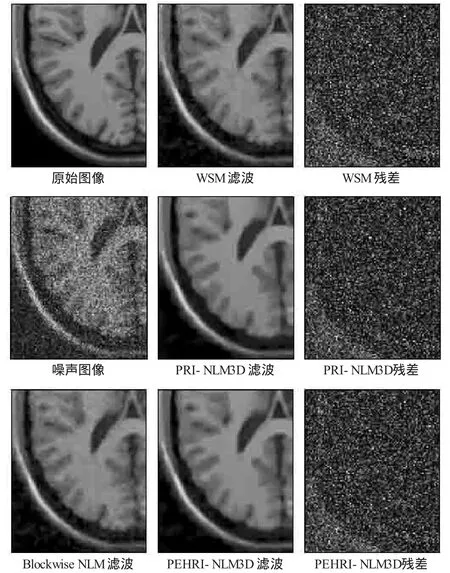
图5 T1w的一个四分之一切片去噪结果（添加14%的莱斯噪声）

3.3 临床数据的应用

为了评价提出的方法在临床数据上的应用，将提出的方法应用于T1w图像（256×256×128个体素，TR=9.7 ms，TE=4 ms，TI=20 ms，TD=200 ms，翻转角=10°，体素分辨率是 1×1×1.25 mm3）。这张图像从OASIS数据库（www.oasisbrains.org）下载得到。使用Coupe等［13］的方法对噪声水平进行估计，图像的噪声水平约是图像最大亮度值的2.4%。图6显示了使用本文提出的方法去噪后的图像和残差绝对值图像。从视觉上看：提出的方法保护了图像的解剖结构，同时很好地去除了噪声。

图6 PEHRI-NLM3D真实数据的实验结果

4 小结

本文提出了一种基于增强的同质相似性和旋转不变性的三维非局部平均滤波方法。提出的方法强调了块状的结构信息，例如边缘、血管、片状。和近年来相关的先进方法在Brainweb数据库进行定量对比，结果表明提出的方法具有有效性。另一个方面，从实际应用的角度上，提出的方法运行在一个合理的时间。对一个标准的数据图像（包含181×217×181个像素）在Matlab 2011a运行多线程C语言MEX文件，所需的时间在1 min以内（电脑配置：Windows XP 64位系统，CPU为Intel Core i5-23002.80 GHz，RAM为8 G）。进一步降低滤波运行时间的方法可以考虑基于GPU的实现［14-15］。

［1］SHATTUCK DW,SANDOR-LEAHY SR,SCHAPERK A,et al.Magnetic resonance image tissue classification using a partial volume model［J］.Neuroimage,2001,13:856-876.

［2］ASHBURNERJ,FRISTONK.Multimodal image coregistration and partitioning-a unified framework［J］.Neuroimage,1997,6:209-217.

［3］BUADESA,COLL B,MOREL J M.A non-local algorithm for image denoising ［C］//IEEE Computer Society Conference Computer Vision Pattern Recognition.Washington:IEEEComputer Society Press,2005:60-65.

［4］MANJON JV,CARBONELL-CABALLEROJ,LULL JJ,et al.MRI Denoising Using Non-Local Means［J］.Medical Image Analysis,2008,12（4）:514-523.

［5］COUPEP,YGERP,PRIMA S,et al.An optimized blockwise nonlocal means denoising filter for 3Dmagnetic resonance images［J］.IEEETrans Med Imaging,2008,27（4）:425-441.

［6］COUPEP,HELLIERP,PRIMA S,et al.3Dwavelet subbands mixing for image denoising［J］.International Journal Biomedical Imaging,2008,2008:1-11.

［7］MANJÓ J V,COUPÉ P,BUADESA,et al.New methods for MRI denoising based on sparseness and self-similarity［J］.Medical Image Analysis,2012,16（1）:18-27.

［8］YUJH,WANGY Y,SHENY Z.Noise reduction and edge detection via kernel anisotropic diffusion ［J］.Pattern Recognition Letters,2008,29:1496-1503.

［9］房少梅.基于非局部泛函分析的图像处理［J］.数学进展,2009,38（6）:649-656.

［10］PETERDJ,GOVINDANV K,MATHEWA T.Nonlocal-Means Image Denoising Technique Using Robust M-Estimator［J］.Journal of Computer Science Technology,2010,25（3）:623-631.

［11］WIEST-DAESSLE N,PRIMA S,COUPE P,et al.Rician Noise Removal by Non-Local Means Filtering for Low Signal-to-Noise Ratio MRI:Applications to DT-MRI［J］.Medical Image Computing and Computer-Assisted Intervention,2008,11:171-179.

［12］WANGZ,BOVIK A C,SHEIKH H R,et al.Image quality assessment:From error visibility to structural similarity［J］.IEEETransactions on Image Processing,2004,13（4）:600-612.

［13］COUPE P,MANJON JV,GEDAMU E,et al.Robust Rician noise estimation for MR images［J］.Medical Image Analysis,2010,14（4）:483-493.

［14］PALHANOXAVIERDEFONTESF,ANDRADEBARROSOG,COUPÉ P,et al.Real time ultrasound image denoising［J］.Journal of Real-Time Image Processing,2011,6（1）:15-22.

［15］GOOSSENSB,LUONG H,AELTERMAN J,et al.A GPU-Accelerated Real-Time NLMeans Algorithm for Denoising Color Video Sequences［C］//Advanced Conceptsfor Intelligent Vision Systems.Berlin:Springer,2010:46-57.