基于双支持向量机的大样本分类算法

胡小生

（佛山科学技术学院电子与信息工程学院，广东佛山528000）

支持向量机（Support Vector Machine，SVM）是基于统计学习理论的机器学习方法，它基于结构风险最小化原则，较好地解决了小样本、非线性、高维数和局部极小等问题，在数字识别、图像识别、文本分类等诸多实际领域得到广泛应用。SVM的训练过程归结为求解一个受约束凸二次规划（Quadratic Programming，QP）问题，对于数量为n的训练样本，其时间复杂度和空间复杂度分别为O（n3）和O（n2），当训练数据规模增大时，算法训练时间和空间的开销会急剧增加，所以不适合用来处理大规模数据。如何借鉴成熟的机器学习方法来提高SVM处理大规模样本数据的效率问题已经成为近年来机器学习领域的一个热点研究方向［1-2］。

近十年来，为了解决SVM对大规模数据集的学习效率问题，学者们进行了大量研究，研究方法大致可分为两类：一类为数值方法，这类方法重点关注如何快速求解SVM的二次规划问题，例如Chen等［3］引入分而治之策略，采用序列最小化优化算法将SVM二次规划问题分解为多个子问题，以提高SVM训练速度；Osuan等［4］提出分解算法将QP问题转化为多个小QP问题；Dong等［5］采用并行优化方法，使用块对角矩阵来代替原始核矩阵，以便减少训练时间；Tsang等［6］提出通过核向量机（Core Vector Machine，CVM）算法求解SVM二次规划问题。上述这些方法在某种程度上提高了算法训练速度，但是对于大规模数据集仍然不够理想，分类精度不稳定；另外一类是数据缩减方法，这类方法通过借助一些其他算法来缩减数据规模，缩减训练集，比如基于随机采样和基于聚类的SVM算法［7-10］，朱芳等［11］提出的基于点集理论的支持向量机大规模训练样本缩减策略，包文颖等［12］提出的基于多粒度数据压缩的支持向量机。基于数据缩减方法没有在本质上解决支持向量机的QP难问题，算法性能关键之处在于所采用的缩减技术，如果缩减技术设计不当，将会严重影响算法的分类性能。

本文采用缩减数据集思想，提出一种双支持向量机算法对大规模样本进行分类，通过两阶段SVM训练来确定最终分类决策模型。首先，采用K均值聚类对初始训练样本进行聚类，提取各簇的聚类质心组成缩减训练集进行初次SVM训练；然后，合并对于训练后获得的支持向量所对应的聚类簇，得到新的训练集，参与第二次的SVM训练，得到最终的决策模型。

1 双支持向量机算法

1.1 SVM算法

对于二分类问题，给定训练样本集D为

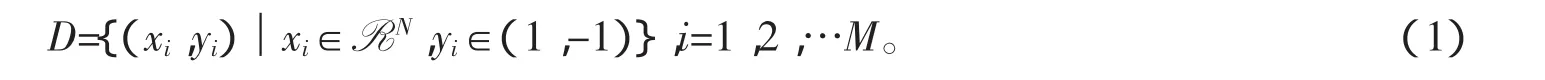
SVM算法的目标是寻找最优分类超平面来最大化两类样本之间的距离。基于一般通用性，考虑训练样本为非线性，引入非线性变换ø：RN→H将样本从输入空间RN映射到高维特征空间H，从而将非线性问题转变为线性问题。当线性可分时，求解最优分类超平面可归纳为如下二次规划问题

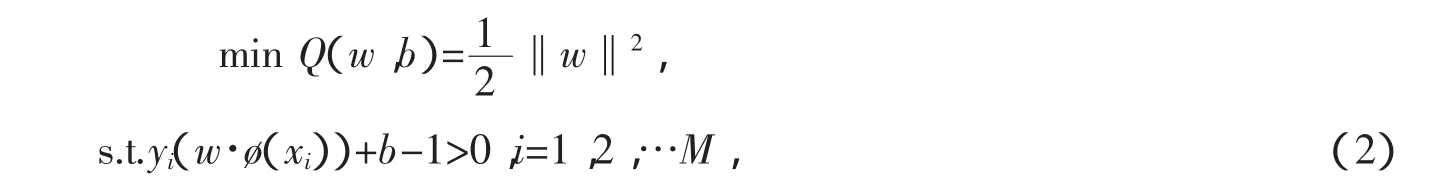
其中，w为权重向量，b为阀值。当线性不可分时，引入惩罚因子C，对错分样本进行惩罚，此时式（2）重写为

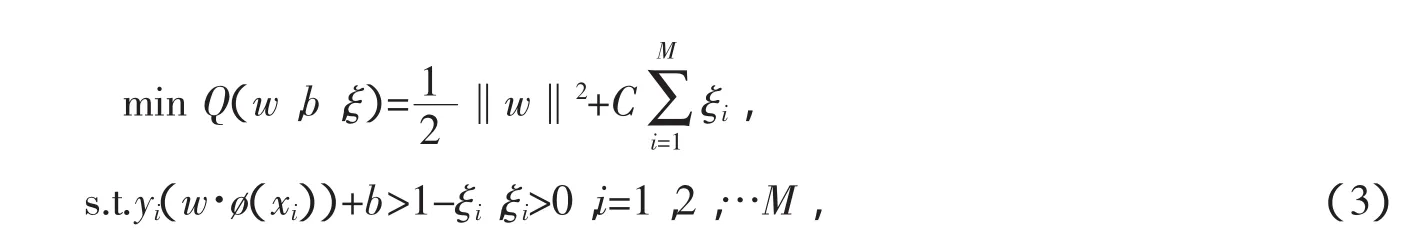
其中，ξ为松弛变量。

利用拉格朗日乘子法求解具有约束的二次规划问题，即

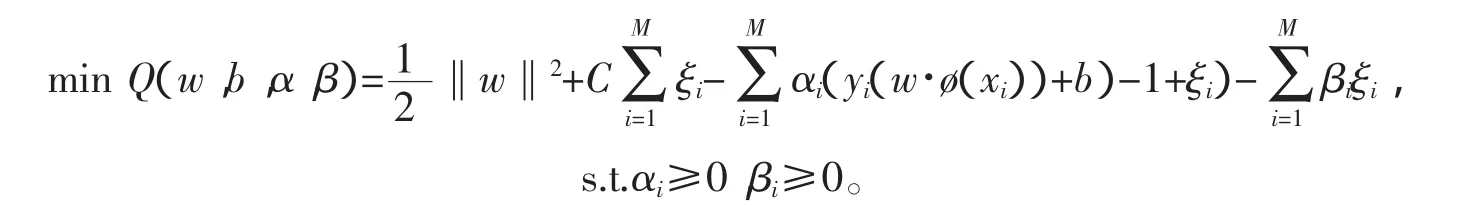
根据约束问题的KKT条件，得

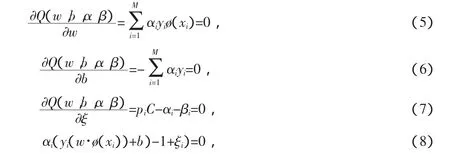
由式（5）得

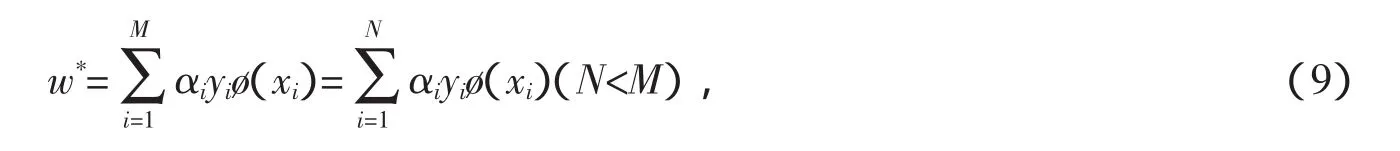
其中，N 为拉格朗日乘子αi＞0所对应的样本（支持向量）总数量。根据式（8）求解阀值b*，（w*，b*）数值确定后，SVM分类决策函数为

其中，K（xi，yi）为高维Hilbert空间中的内积。

1.2 初次快速SVM训练

从SVM的模型原理中可以看出：给定的训练样本中只有一小部分样本点（支持向量，式（9）中的N，N＜＜M）决定了分类超平面，其余训练样本对于分类超平面以及分类决策函数的建立是无用信息甚至是干扰噪声样本。但是SVM模型训练之前，并不知道哪些样本是有用的支持向量，它将所有样本点进行训练并建模，这样，一方面无用甚至是干扰噪声样本的输入，导致了大量不必要的计算和存储空间，另一方面有可能导致模型识别性能的下降和学习推广能力的降低。如果在模型训练之前，通过某种数据预处理方法，从初始训练样本中筛选出最有可能的支持向量样本范围，就可以在一定程度上改善上述问题。

给定一个数据集合，从数据挖掘的角度来看，精简样本集规模，去除冗余样本的最直接方法是提取样本集中的代表集，用少量的代表样本集代替全部数据集，而聚类是数据挖掘领域用来提取有用信息的方法之一。K-means是一种基于划分的聚类算法，具有算法简单、输入参数少、计算速度快和对大规模数据效率高的优点，本文首先选用K-means对初始训练集的正、负类分别进行聚类，然后提取每个聚类簇中的聚类质心作为代表样本，组成新的缩减训练集，参与初次SVM模型训练。具体的步骤如下：

（1）对于正类、负类样本分别为n1、n2的训练样本集，对每类样本分别进行K-means聚类，其中聚类的输入参数k1、k2按照大拇指准则确定

（2）提取所有的聚类质心，以及其对应的类别标签y=［1，-1］组成缩减数据集；（3）缩减数据集参与SVM训练，得到决策支持向量。

1.3 二次SVM训练

对SVM来说，支持向量集等价于训练数据全集，预选支持向量能排除大量无关训练样例，加速训练时间，但是支持向量是通过计算目标函数得到的，所得结果是精确的；预选支持向量是通过非优化方法得到的，所得结果是近似的，预选支持向量集可能包括真实的支持向量，也可能漏掉某些支持向量。

分析SVM模型过程可知，其分类超平面由支持向量决定，大量的居于分类超平面的边界样本点决定了分类超平面的偏移方向，初次SVM训练目的旨在快速确定支持向量的大致范围，为了得到更精确的分类决策函数，第二次SVM训练需要更精准的训练集。在初次快速SVM训练基础上，对于那些成为支持向量的所有聚类质心，将其所对应聚簇内的所有样本点合并，组成一个更具代表性的训练样本集，参与第二次SVM训练。参与第二次的训练样本集与初始训练集相比，在预选支持向量范围大致涵盖的情况下，其数据规模大幅度减小，减少了模型的训练时间。整个基于双支持向量机的大样本分类算法流程如图1所示。

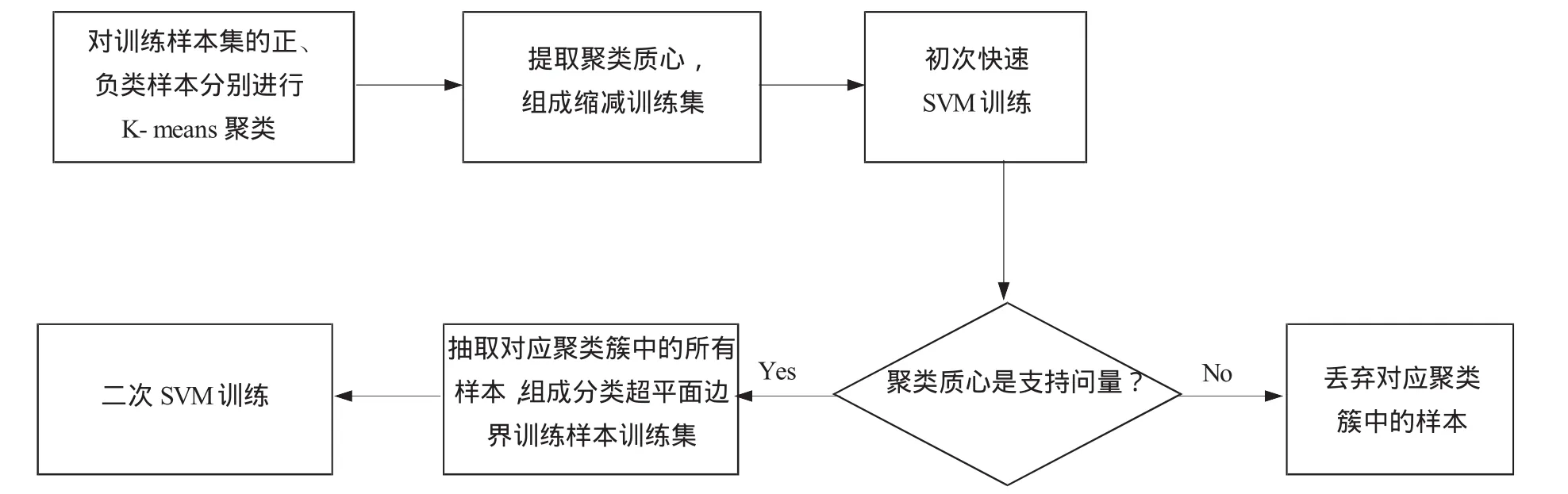
图1 双支持向量机的大样本分类算法流程图

2 实验与分析

实验环境为:新西兰怀卡托大学开发的基于Java的开源数据挖掘平台Weka3.6，个人PC配置如下:PentiumDual-core 2.5 G CPU，2 G内存，Windows 732位操作系统，Matlab7.4.0，选用RBF核函数。实验数据选择5组具有不同实际应用背景的UCI数据，对于含有多个类别的数据，为了降低类别不平衡对算法性能的影响，采用与其他文献相似的方法：合并其中的一些类作为正类，合并剩下的各个类别成为负类，以便正、负类大致平衡，相关信息如表1所示。

表1 UCI数据集信息

为了说明本文方法的有效性，分别采用LibSVM、基于聚类的支持向量机Cluster-SVM、基于随机下采样的支持向量机Random-SVM与本文算法Dual-SVM，在分类精度和模型训练时间这两个评价标准上进行比较。

为方便比较，实验中对数据采用十折交叉验证方式，每次将其中9个子集作为训练集，1个子集作为测试集，重复10次，以平均值作为最终的分类结果，相关结果如表2、3所示。

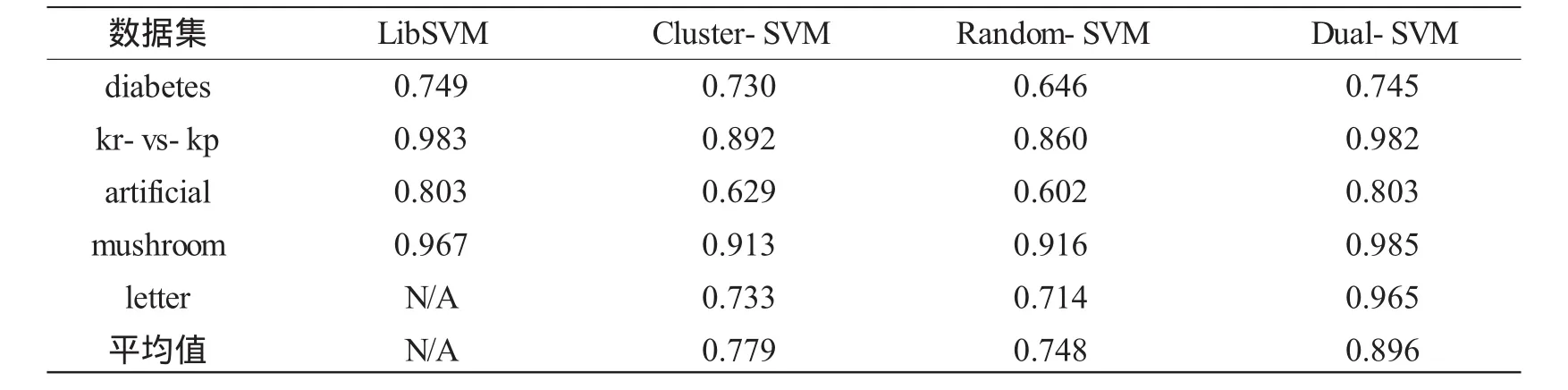
表2 不同算法的分类精度 %

从表2可以看出，本文所提的方法具有很好的分类效果，在所测试的5个数据集上的分类准确率明显比基于聚类的支持向量机Cluster-SVM和基于随机下采样的支持向量机Random-SVM方法高，究其原因，Cluster-SVM和Random-SVM虽然能够减少训练样本规模，但是在减少样本的同时，会明显漏掉一些潜在的决策支持向量，导致模型的泛化能力下降。本文算法与流行的支持向量机算法LibSVM相比，在相关数据规模稍小的diabetes、kr-vs-kp、arfificial和mushroom数据集上，二者整体分类准确率相当，但是对于letter数据集，在本实验环境配置下，算法实施超出了内存容量，不能继续进行，劣势明显。

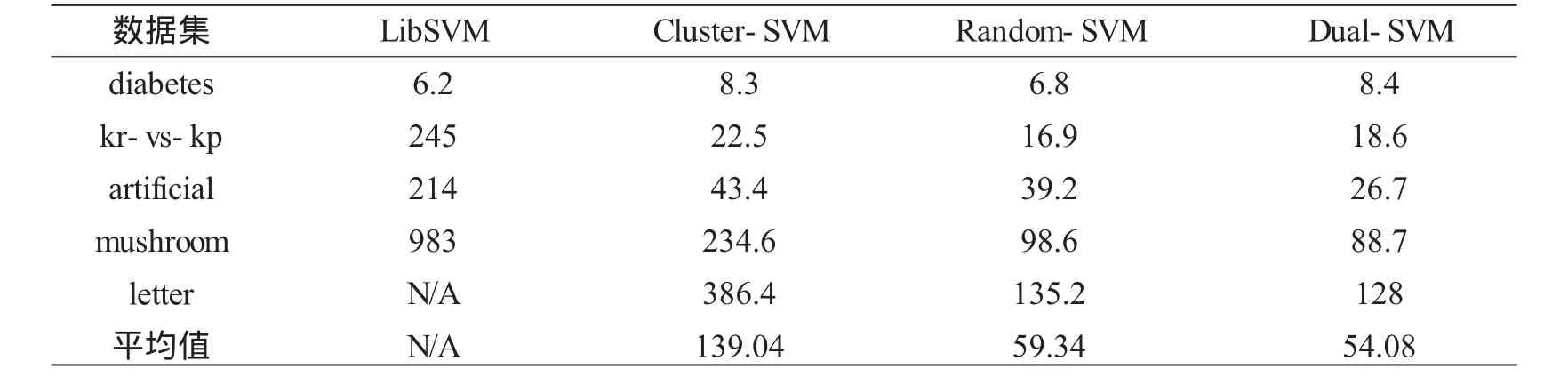
表3 不同算法的模型训练时间 s

从表3可以看出，本文算法的模型训练时间要远小于LibSVM，并且随着训练样本数量的扩大，其训练模型在时间花费上的优势越来越明显；本文算法与Random-SVM在训练时间上相当，但是分类准确率明显优于后者；与Cluster-SVM相比，无论是分类准确率，还是模型训练时间，都有明显优势。

3 小结

本文采用缩减训练集的方法来解决SVM对于大规模数据集的分类瓶颈问题。对于支持向量机，分类决策函数仅仅与训练集中的少部分支持向量有关，通过预选支持向量范围，可有效剔除对建立模型无关的冗余样本。本文通过基于聚类的初次快速SVM训练获得最优分类超平面，以确定边界样本集，然后合并所有边界样本集以组成缩减的最终训练集，参与二次SVM训练，得到最终的分类模型。实验结果表明，本文方法在降低学习时间的同时，很好地保证了分类器的分类精度。

［1］张宇,王文剑,郭虎升.基于粒分布的支持向量机加速训练方法［J］.南京大学学报:自然科学版,2013,49（5）:639-644.

［2］李琳,伍少梅,唐宁九.基于中心加权的局部核向量机算法［J］.电子科技大学学报,2014,43（4）:612-617.

［3］CHEN P H,FAN R E,LIN C J.A study on SMO-type decomposition methods for support vector machines ［J］.IEEE Transactionson Neural Networks，2006,17（4）:893-908.

［4］OSUAN E,FRENUD R,GIROSI F.An improved training algorithm for support vector machines［C］//Proceedings of IEEE Workshop on Neural Networks for Signal Processing.New York:ACMPress,1997:276-285.

［5］DONG JX,KRZYZAK A,SUEN C Y.Fast SVM training algorithm with decomposition on very large data sets ［J］.IEEE Transactionson Pattern Analysisand Machine Intelligence,2005,27（4）:603-618.

［6］TSANGIW,KWOKJT,ZURADAJM.Generalized corevector machines［J］.IEEETransactionson Neural Networks,2006,17（5）:1126-1140.

［7］EMRE CO,AHMET A.A new training method for support vector machines:Clustering K-NN support vector machines［J］.Expert Systemswith Applications,2008,35（1）:564-568.

［8］张永,浮盼盼,张玉婷.基于分层聚类及重采样的大规模数据分类［J］.计算机应用,2013,33（10）:2801-2803.

［9］覃希,苏一单.用双层减样法优化大规模SVM垃圾标签检测模型［J］.计算机应用研究,2011,28（6）:2095-2098.

［10］胡小生,钟勇.基于加权聚类质心的SVM不平衡分类方法［J］.智能系统学报,2013,8（3）:261-265.

［11］朱芳,顾军华,杨欣伟.一种新的支持向量机大规模训练样本集缩减策略［J］.计算机应用,2009,49（5）:637-643.

［12］包文颖,胡清华,王长忠.基于多粒度数据压缩的支持向量机［J］.南京大学学报:自然科学版,2013,28（6）:2095-2098.