Understanding ductile-to-brittle transition of metallic glasses from shear transformation zone dilatation

M.Q.Jiang∗,G.Wilde,F.Jiang,L.H.Dai∗

aState Key Laboratory of Nonlinear Mechanics,Institute of Mechanics,Chinese Academy of Sciences,Beijing 100190,China

bInstitute of Materials Physics,Westfälische Wilhelms-Universität Münster,Münster 48149,Germany

cState Key Laboratory for Mechanical Behavior of Materials,Xi’an Jiaotong University,Xi’an 710049,China

Understanding ductile-to-brittle transition of metallic glasses from shear transformation zone dilatation

M.Q.Jianga,∗,G.Wildeb,F.Jiangc,L.H.Daia,∗

aState Key Laboratory of Nonlinear Mechanics,Institute of Mechanics,Chinese Academy of Sciences,Beijing 100190,China

bInstitute of Materials Physics,Westfälische Wilhelms-Universität Münster,Münster 48149,Germany

cState Key Laboratory for Mechanical Behavior of Materials,Xi’an Jiaotong University,Xi’an 710049,China

H I G H L I G H T S

•Cooperative shearing of shear transformation zones(STZs)is assisted by free volume.

•STZ dilatational strain is introduced to understand the ductile-to-brittle transition(DBT)of metallic glasses.

•The DBT of metallic glasses is underpinned by the transition of STZs to tension transformation zones(TTZs).

A R T I C L E I N F O

Article history:

Accepted 5 September 2015

Available online 28 September 2015

Ductile-to-brittle transition

Metallic glass

Fracture

Shear transformation zone

Tension transformation zone

A theoretical model that takes into account the free-volume aided cooperative shearing of shear transformation zones(STZs)is developed to quantitatively understand the ductile-to-brittle transition (DBT)of metallic glasses.The STZ dilatational strain is defined as the ratio of STZ-activated free volume to STZ volume itself.The model demonstrates that the STZ dilatational strain will increase drastically and exceed the characteristic shear strain of STZ as temperature decreases below a critical value.This critical temperature is in good agreement with the experimentally measured DBT temperature.Our results suggestthatthe DBT ofmetallic glasses is underpinned by the transition ofatomic-cluster motions from STZ-type rearrangements to dilatational processes(termed tension transformation zones(TTZs)).

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).

At temperatures well below the glass transition temperature, metallic glasses usually share an avenue to mechanical failure by shear-induced dilatation or free volume generation[1–5]resulting from a cascade of inelastic rearrangements of local atomic clusters, commonly called shear transformation zones(STZs)[6–8].Macroscopically,such a shear-softening process appears as a runaway of shear bands of about 10 nm in thickness into crack propagation through the Saffman–Taylor flow instability[9],leaving microscale vein-like fracture patterns.However,recent experiments [10–13]and simulations[14,15]have revealed that the dilatation itself,whether induced by shear or hydrostatic tension,can dominate brittle fracture of metallic glasses.In this case,the crack tip propagates via cavitating events that involve a series of nanovoids nucleation and coalescence with very limited plastic growth [11,14],which retains the tip atomically sharp during propagation[16,17].The dilatation-mediated brittle fracture is strongly supported by the resulting fracture morphologies[10–12,18–21]: very-fine dimples and nanoscale periodic corrugations.At the atomic scale,such a brittle cavitating event has been originally defined by Jiang et al.[11,22]as a tension transformation zone(TTZ) that describes the atomic cluster motion undergoing significant dilatation.For convenience of understanding,the TTZ can be regarded as a dilatation-dominated STZ,but the later is usually sheardominated[6,7,23].

It is therefore expected that the ductile-to-brittle transition (DBT)of metallic glasses will take place if the STZs at the crack tip are restrained,whereas the TTZs are activated simultaneously. More specifically,the DBT is trigged by the change in the nature of the‘‘transformation zones’’from STZ-type to TTZ-type[11,19, 21,24–26].Nevertheless,why and how an STZ could convert into a TTZ remains to be further clarified.Very recently,we performed systematic experiments on the fracture behavior of a typical Zrbased(Vitreloy 1)bulk metallic glass at decreasing temperature from room temperature(300 K)to liquid helium temperature (4.2 K)[27].It was observed that the cryogenic temperature can incur a sharp DBT at about 20 K,which motivates us to explorethe critical condition for the STZ-to-TTZ transition.In the present letter,we propose a STZ dilatational strain to quantitatively characterize the STZ-to-TTZ transition by taking free volume into the cooperative shearing of STZs.This model is supported by the good agreement between the predicted DBT temperature and that determined experimentally[27].

It has been recognized that plastic flow of metallic glasses occurs as a result of a series of STZ operations[2,6,7,28].However, unlike the unit glide of a dislocation in a crystalline material that is only driven by the deviatoric stress,the potential STZs require local dilatation or free volume for the shear transformations to take place[2,29].In fact,the STZs initiate easier in regions where the free volume is higher[8],although the STZ operation is sheardominated[2,23].We could thus envision an extreme situation in which an STZ experiences a remarkable dilatation rather than shearing,so that the STZ actually becomes a cavitation event, i.e.,the TTZ operation per se defined previously[11].The TTZs ahead the crack tip are widely believed to be responsible for the brittle fracture of metallic glasses[11,19,24,25,27].Hence, how to characterize the dilatation degree of STZ holds a key to the microscopic STZ-to-TTZ transition or the macroscopic DBT in metallic glasses.

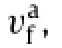
This definition means that if the active free volume or the absolute dilatation of an STZ is comparable to the STZ volume itself,the STZ will be prone to undergo a significant dilatation.When the STZ dilatational strain exceeds a threshold,the STZ becomes a TTZ-type cavitation operation.It should be pointed out that the STZ dilatational strain defined here is somewhat different from the cavitational strain defined by Guan et al.[15].The former mainly addresses the nucleation of a void due to shear(STZ)-induced dilatation,while the latter describes the void nucleation and plastic growth under a direct hydrostatic tension.

The cooperative shearing model(CSM)of STZs points out that the plastic flow occurs in metallic glasses when the barrier crossing rate ofSTZs reaches a criticalvalue comparable to the applied strain rate[31].Considering that the STZ activation is usually assisted by free volume[2,6,29],we generalize this onset condition to involve the configurational(or free volume)probability,Fξ,of the activation of STZs that is statistically related to the free volume by[8,32]

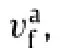
whereγ0is the characteristic shear strain of an STZ,ω0is an attempt frequency,Wτis the activation energy for an STZ at finite shear stress,kBis the Boltzmann constant,C is a dimensionless constant of order unity,and˙γis the applied shear strain rate. Following Johnson and Samwer[31],the activation energy for an STZ to flow in a stressed metallic glass can be written as

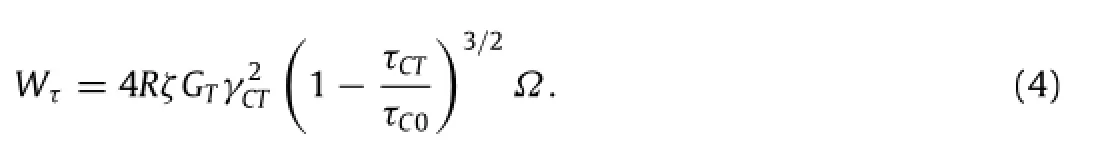
In this equation,R is the‘‘fold ratio’’,ζis a correction factor arising from the matrix confinement.GTis the temperature-dependent shear modulus that can be obtained by[34]

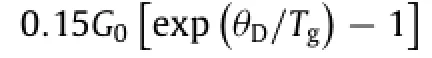
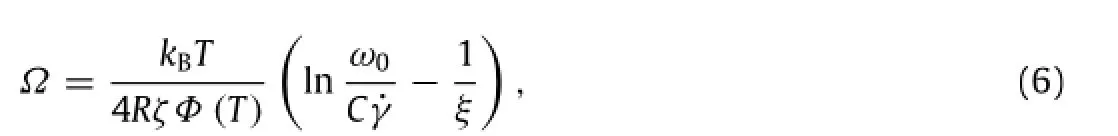
As for the temperature dependence of active free volume,we borrow from a result of the simulation by Starr et al.[35].It is suggested that the evolution of the active free volume with STZ operations at T＜Tgcan be well approximated by a power law

Next,we examine the effect of the environmental temperature on STZ volume(6),active free volume(7),and STZ dilatational strain(1),by using Vitreloy 1 as a modelmaterial.The relevant mechanicaland physicalparameters of Vitreloy 1 are derived fromthe recent literature[3,8,29,31,39–41]and listed in Table 1.By combining Eqs.(6)and(7),the evolution of active free volume and STZ volume with temperature is calculated in Fig.1.The calculated free volume and STZ volume are,respectively,comparable to the experimentally determined values[39,42,43].Itcan be seen thatboth STZ volume and STZ-activated free volume decrease monotonously and approach zero with decreasing temperature.This result implies that low temperatures render plastic flow more difficult.It isbecause that the STZ volume becomes smaller at lower temperatures,so that flow requires a relatively larger number of STZs, which,however,are difficult to synchronously cooperate during shearing[23].Furthermore,the active free volume becomes more insufficient with decreasing temperature,which in turn delays the activation of STZ and increases its activation stress[29].This is consistent with the common observation of low-temperature strengthening of shear failure of metallic glasses[27,44–46].The physical rationality of Fig.1 can be understood if we compare the STZ for flow of glassy solids to the cooperatively rearranging regions(CRRs)for relaxation of glassy liquids.Recently,Stevenson et al.[47]have found that with the temperature decreasing from the mode coupling critical temperature to the Kauzmann temperature,the CRR shape will change from a loose configuration to a compact one,and the characteristic size of CRR decreases correspondingly.Itis expected that the more compact CRRs with smaller size have smaller free volume.However,we note thateither the active free volume or the STZ volume alone cannot naturally predict the occurrence of the DBT.

Consequently,we further examine the STZ dilatational strain defined by Eq.(1).A plot of the STZ dilatational strain as a function of temperature is shown in Fig.2,where the fracture strengths of Vitreloy 1 are also denoted at different temperatures[27].An obvious DBT temperature of about 20 K can be experimentally identified,based on the observation that the fracture strengths change from constant to discrete at a fixed temperature.Very interestingly and surprisingly,we find that,when the temperature decreases below 20 K,the STZ dilatational strain shows a sudden jump and its value can even reach up to 100%.This result implies an emergence of a TTZ-type atomic cluster motion that can be considered as a transient activation from a STZ with significant dilatation at very low temperatures.It is well known that the characteristic shear strain of a STZ is about 10%[6,8].If we roughly adopt the STZ dilatational strain of 10%as the threshold for the TTZ activation,a critical transition temperature can be predicted to be about 15 K.The predicted value is very close to the experimentally measured DBT temperature(about 20 K).Recently,a simulation work performed by Murali et al.[14]also provides an important information about the critical volumetric strain for nanoscale cavitation.It can be found that,in a brittle Fe80P20glass,the peak hydrostatic stress that just achieves the critical cavitation stress is insensitive to the initial void volume fraction;more importantly, the corresponding critical cavitational strain is also almost universal(about 12%).This critical cavitational strain is very close to our predicted STZ dilatational strain(10%)for the occurrence of the STZ-to-TTZ at the DBT temperature.Furthermore,the present picture regarding the STZ-to-TTZ transition(Fig.2)rules out the possibility that the active free volume or the STZ volume will decrease to zero in the zero temperature limit(Fig.1).

At temperatures above 20 K,the dilatational strain keeps a very low level(about 10−4),much smaller than the characteristic shear strain of STZs by three orders of magnitude,and is almost insensitive to the temperature.The extremely small dilatation confirms that the STZ operations are volume conserving events of rearrangements[23]and still predominate the shear fracture of materials at T＞20 K.Actually,in the temperature range(T＞20 K),the temperature-dependent strength can be well predicted by the Johnson–Samwer T2/3law[31]that has the form:

Table 1Mechanical and physical parameters for Vitreloy 1 metallic glass.

Fig.1.Evolution of shear transformation zone volume(Eq.(6))and active free volume(Eq.(7))with temperature.

Fig.2.STZ dilatational strain(Eq.(1))and fracture strength[27]as a function of temperature.At temperatures above 20 K,the temperature-dependent strength follows the Johnson–Samwer T2/3law expressed by Eq.(8).

whereσf,0=2.22 GPa is the athermal ductile fracture strength, andΓ=0.01 GPa·K−2/3is the temperature softening coefficient. Eq.(8)is shown in Fig.2 as the dashed line.The agreementconfirms that the cooperative shear motions of STZs at the crack tip dominate the ductile fracture of metallic glasses[11,14,24]. However,the STZ model breaks down at very low temperatures due to the DBT intervention below a critical temperature(here about 20 K for as-cast Vitreloy 1[27]).

Our theoretical results(Figs.1 and 2),together with the experimental observations[27],shed light on the cryogenictemperature-induced DBT mechanism in fracture of metallic glasses,which is schematized in Fig.3.At room temperature,the STZ is shear-dominated,accompanying a very limited dilatation (∼10−4).The activation of one STZ gives rise to an‘‘Eshelby’’-type localized shear distortion in the surrounding elastic medium[6], and triggers an avalanche-like behavior of neighboring STZs to form shear banding[28,48–50],leading to a macroscopic sheardominated fracture.With decreasing temperature,the characteristic size of STZs(or the number of atoms participating in an STZ) reduces rapidly,which implies that the fraction of the surrounding elastic medium will increase.A direct consequence is that the activation of STZ needs to surmount a higher energy barrier and thus requires a higher activation stress for operations.This is why the fracture strength of metallic glasses will increase as temperature lowers,showing the shear strengthening behavior at T＞20 K(Fig.2).At the same time,the capability of STZ to create free volume reduces due to the difficulty in activation of STZs,which keeps the dilatation degree of STZs at a very low level.When temperature decreases below a critical temperature,the dilatational strain of STZ will drastically grow,corresponding to an essential change of the cluster motion from shear-dominated STZ into dilatation-dominated TTZ.This critical transition originates from the significant difference in the temperature dependence of the STZ-activated free volume and the STZ volume(see Fig.1).Macroscopically,the STZ-to-TTZ transition corresponds to the change of the fracture modes from ductile(shear)to brittle(dilatational)in metallic glasses[27],which is verified by the almost identical critical temperature of both transitions(see Fig.2).

Based on the free-volume assisted cooperative shearing of STZs, the concept of STZ dilatational strain is proposed to understand the underlying mechanism for the DBT of metallic glasses in fracture.It is predicted that the DBT will take place when the dilatational strain of STZs increases dramatically,and exceeds their characteristic shear strain,corresponding to an STZ-to-TTZ transition.The predicted DBT temperature agrees well with the experimentally observed[27].Our work implies that the relative contribution of shear to dilatation of STZs or the intrinsic competition between STZ and TTZ is temperature-dependent, and further substantiates the idea that very-low-temperature or athermal STZs are inclined to undergo a dilatational TTZ mode. In fact,our model shows that the STZ dilatational strain depends not only on temperature,but also on composition/structure or loading conditions.As predicted by Eq.(6),decreasing free volume and/or increasing strain rate will also result in a smaller STZ size, thus incurs a higher STZ dilatational strain or a brittle fracture. Therefore,the picture of STZ(shear)versus TTZ(dilatation)leads to an improved understanding of the DBT of metallic glasses,and is also consistent with the well-known Poisson’s ratio criterion for plasticity of amorphous solids[51–53].

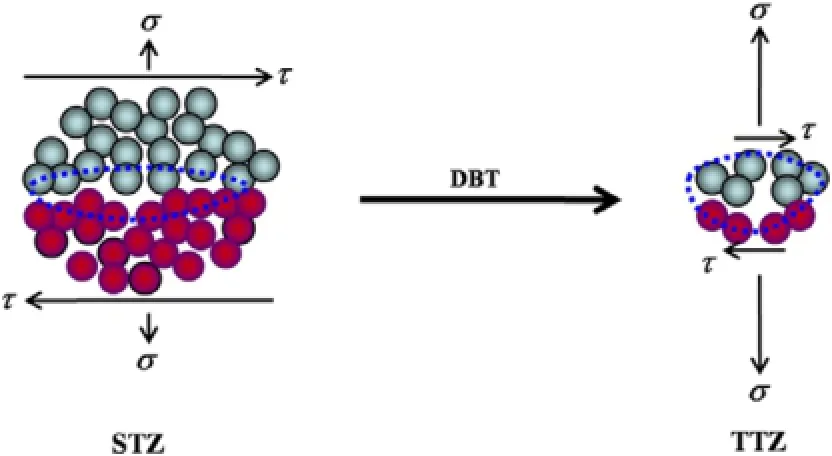
Fig.3.Two-dimensionalschematics ofthe transition ofatomic cluster motion from shear-dominated STZ to dilatation-dominated TTZ at a DBT temperature.

Acknowledgments

The authors are very gratefulto Prof.K.Samwerforenlightening discussions.This work was supported by the National Nature Science Foundation of China(Grant Nos.11522221,11372315, 11472287,and 51171138),the National Basic Research Program of China(Grant No.2012CB937500),the CAS/SAFEA International Partnership Program for Creative Research Teams,and partially also by DFG.

References

[1]F.Spaepen,A microscopic mechanism for steady state inhomogeneous flow in metallic glasses,Acta Metall.25(1977)407–415.

[2]A.Lemaître,Rearrangements and dilatancy for sheared dense materials,Phys. Rev.Lett.89(2002)195503.

[3]M.Q.Jiang,L.H.Dai,On the origin of shear banding instability in metallic glasses,J.Mech.Phys.Solids 57(2009)1267–1292.

[4]A.Furukawa,H.Tanaka,Inhomogeneous flow and fracture of glassy materials, Nature Mater.8(2009)601–609.

[5]H.H.Ruan,L.C.Zhang,J.Lu,A new constitutive model for shear banding instability in metallic glass,Int.J.Solids Struct.48(2011)3112–3127.

[6]A.S.Argon,Plastic deformation in metallic glasses,Acta Metall.27(1979) 47–58.

[7]M.L.Falk,J.S.Langer,Dynamics of viscoplastic deformation in amorphous solids,Phys.Rev.E 57(1998)7192–7205.

[8]C.A.Schuh,T.C.Hufnagel,U.Ramamurty,Mechanical behavior of amorphous alloys,Acta Mater.55(2007)4067–4109.

[9]A.S.Argon,M.S.Salama,The mechanism of fracture in glassy material capable of some inelastic deformation,Mater.Sci.Eng.23(1976)219–230.

[10]G.Wang,D.Q.Zhao,H.Y.Bai,et al.,Nanoscale periodic morphologies on the fracture surface of brittle metallic glasses,Phys.Rev.Lett.98(2007)235501.

[11]M.Q.Jiang,Z.Ling,J.X.Meng,et al.,Energy dissipation in fracture of bulk metallic glasses via inherent competition between local softening and quasicleavage,Phil.Mag.88(2008)407–426.

[12]E.Bouchaud,D.Boivin,J.L.Pouchou,et al.,Fracture through cavitation in a metallic glass,Europhys.Lett.83(2008)66006.

[13]X.Huang,Z.Ling,H.S.Zhang,et al.,How does spallation microdamage nucleate in bulk amorphous alloys under shock loading?J.Appl.Phys.110(2011) 103519.

[14]P.Murali,T.F.Guo,Y.W.Zhang,et al.,Atomic scale fluctuations govern brittle fracture and cavitation behavior in metallic glasses,Phys.Rev.Lett.107(2011) 215501.

[15]P.Guan,S.Lu,M.J.B.Spector,et al.,Cavitation in amorphous solids,Phys.Rev. Lett.110(2013)185502.

[16]R.L.Narayan,P.Tandaiya,R.Narasimhan,et al.,Wallner lines,crack velocity and mechanisms ofcrack nucleation and growth in a brittle bulk metallic glass, Acta Mater.80(2014)407–420.

[17]R.Narasimhan,P.Tandaiya,I.Singh,et al.,Fracture in metallic glasses: mechanics and mechanisms,Int.J.Fract.191(2015)53–75.

[18]X.K.Xi,D.Q.Zhao,M.X.Pan,et al.,Fracture of brittle metallic glasses: Brittleness or plasticity,Phys.Rev.Lett.94(2005)125501.

[19]F.Jiang,M.Q.Jiang,H.F.Wang,et al.,Shear transformation zone volume determining ductile–brittle transition of bulk metallic glasses,Acta Mater.59 (2011)2057–2068.

[20]G.Li,M.Q.Jiang,F.Jiang,et al.,Temperature-induced ductile-to-brittle transition of bulk metallic glasses,Appl.Phys.Lett.102(2013)171901.

[21]G.Li,M.Q.Jiang,F.Jiang,et al.,The ductile to brittle transition behavior in a Zr-based bulk metallic glass,Mater.Sci.Eng.A-Struct.625(2015)393–402.

[22]M.Q.Jiang,Z.Ling,J.X.Meng,et al.,Nanoscale periodic corrugation to dimple transition due to beat in a bulk metallic glass,Scr.Mater.62(2010)572–575.

[23]M.L.Falk,J.S.Langer,L.Pechenik,Thermal effects in the shear-transformationzone theory ofamorphous plasticity:Comparisons to metallic glass data,Phys. Rev.E 70(2004)011507.

[24]R.Raghavan,P.Murali,U.Ramamurty,On factors influencing the ductile-tobrittle transition in a bulk metallic glass,Acta Mater.57(2009)3332–3340.

[25]J.P.Escobedo,Y.M.Gupta,Dynamic tensile response of Zr-based bulk amorphous alloys:Fracture morphologies and mechanisms,J.Appl.Phys.107 (2010)123502.

[26]X.Huang,Z.Ling,L.H.Dai,Ductile-to-brittle transition in spallation of metallic glasses,J.Appl.Phys.116(2014)143503.

[27]M.Q.Jiang,G.Wilde,J.H.Chen,et al.,Cryogenic-temperature-induced transition from shear to dilatational failure in metallic glasses,Acta Mater.77 (2014)248–257.

[28]A.Lemaître,C.Caroli,Rate-dependent avalanche size in athermally sheared amorphous solids,Phys.Rev.Lett.103(2009)065501.

[29]M.Q.Jiang,G.Wilde,L.H.Dai,Origin of stress overshoot in amorphous solids, Mech.Mater.81(2015)72–83.

[30]D.Turnbull,M.H.Cohen,Free-volume model of the amorphous phase:glass transition,J.Chem.Phys.34(1961)120–125.

[31]W.L.Johnson,K.Samwer,A universal criterion for Plastic yielding of metallic glasses with a(T/Tg)2/3temperature dependence,Phys.Rev.Lett.95(2005) 195501.

[32]M.Heggen,F.Spaepen,M.Feuerbacher,Creation and annihilation of free volume during homogeneous flow of a metallic glass,J.Appl.Phys.97(2005) 033506.

[33]M.Q.Jiang,W.H.Wang,L.H.Dai,Prediction of shear-band thickness in metallic glass,Scr.Mater.60(2009)1004–1007.

[34]Z.Y.Zhang,V.Keppens,T.Egami,A simple model to predict the temperature dependence of elastic moduli of bulk metallic glasses,J.Appl.Phys.102(2007) 123508.

[35]F.W.Starr,S.Sastry,J.F.Douglas,et al.,What do we learn from the local geometry of glass-forming liquids?Phys.Rev.Lett.89(2002)125501.

[36]W.Dmowski,T.Iwashita,C.P.Chuang,et al.,Elastic heterogeneity in metallic glasses,Phys.Rev.Lett.105(2010)205502.

[37]M.H.Cohen,G.S.Grest,Liquid-glass transition,a free-volume approach,Phys. Rev.B 20(1979)1077–1098.

[38]G.Adam,J.Gibbs,On the temperature dependence of cooperative relaxation properties in glass-forming liquids,J.Chem.Phys.43(1965)139–146.

[39]A.Masuhr,T.A.Waniuk,R.Busch,et al.,Time scales for viscous flow,atomic transport,and crystallization in the liquid and supercooled liquid states of Zr41.2Ti13.8Cu12.5Ni10.0Be22.5,Phys.Rev.Lett.82(1999)2290–2293.

[40]Y.Q.Cheng,E.Ma,Intrinsic shear strength of metallic glass,Acta Mater.59 (2011)1800–1807.

[41]W.H.Wang,The elastic properties,elastic models and elastic perspectives of metallic glasses,Prog.Mater.Sci.57(2012)487–656.

[42]Z.Evenson,R.Busch,Equilibriumviscosity,enthalpy recovery and free volume relaxation in a Zr44Ti11Ni10Cu10Be25bulk metallic glass,Acta Mater.59(2011) 4404–4415.

[43]D.Pan,A.Inoue,T.Sakurai,et al.,Experimental characterization of shear transformation zones for plastic flow of bulk metallic glasses,Proc.Natl.Acad. Sci.105(2008)14769–14772.

[44]H.Q.Li,G.Fan,K.X.Tao,etal.,Compressive behaviorofa Zr-based metallic glass at cryogenic temperatures,Adv.Mater.18(2006)752–754.

[45]A.Dubach,F.H.Dalla Torre,J.F.Loffler,Constitutive model for inhomogeneous flow in bulk metallic glasses,Acta Mater.57(2009)881–892.

[46]A.Kawashima,Y.Yokoyama,I.Seki,et al.,Enhanced tensile strength and plasticity of Zr–Cu–Al bulk glassy alloys at cryogenic temperatures,Mater. Trans.50(2009)2685–2690.

[47]J.D.Stevenson,J.Schmalian,P.G.Wolynes,The shapes of cooperatively rearranging regions in glass-forming liquids,Nat.Phys.2(2006)268–274.

[48]A.S.Argon,Strain avalanches in plasticity,Phil.Mag.93(2013)3795–3808.

[49]W.Jiao,B.A.Sun,P.Wen,et al.,Crossover from stochastic activation to cooperative motions of shear transformation zones in metallic glasses,Appl. Phys.Lett.103(2013)081904.

[50]J.Antonaglia,W.J.Wright,X.J.Gu,et al.,Bulk metallic glasses deform via slip avalanches,Phys.Rev.Lett.112(2014)155501.

[51]J.J.Lewandowski,W.H.Wang,A.L.Greer,Intrinsic plasticity or brittleness of metallic glasses,Phil.Mag.Lett.85(2005)77–87.

[52]M.Q.Jiang,L.H.Dai,Short-range-order effects on intrinsic plasticity of metallic glasses,Phil.Mag.Lett.90(2010)269–277.

[53]G.N.Greaves,A.L.Greer,R.S.Lakes,etal.,Poisson’s ratio and modern materials, Nature Mater.10(2011)823–837.

30 July 2015

∗.Tel.:+86 10 52843931;fax:+86 10 82543977.

E-mail addresses:mqjiang@imech.ac.cn(M.Q.Jiang),lhdai@lnm.imech.ac.cn (L.H.Dai).

http://dx.doi.org/10.1016/j.taml.2015.09.002

2095-0349/©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*This article belongs to the Solid Mechanics