Experimental study on interaction between a positive mass and a negative effective mass through a mass–spring system

Jio Zhou,Yong Cheng,Hongkun Zhng,Guoling Hung,Gengki Hu,∗

aKey Laboratory of Dynamics and Control of Flight Vehicle,Ministry of Education,School of Aerospace Engineering,Beijing Institute of Technology, Beijing 100081,China

bDepartment of Mechanical and Aerospace Engineering,University of Missouri,Columbia,MO,65211,USA

Experimental study on interaction between a positive mass and a negative effective mass through a mass–spring system

Jiao Zhoua,Yong Chenga,Hongkuan Zhanga,Guoliang Huangb,Gengkai Hua,∗

aKey Laboratory of Dynamics and Control of Flight Vehicle,Ministry of Education,School of Aerospace Engineering,Beijing Institute of Technology, Beijing 100081,China

bDepartment of Mechanical and Aerospace Engineering,University of Missouri,Columbia,MO,65211,USA

H I G H L I G H T S

•We investigate the dynamics of a positive mass and a negative mass chain,which shows the two bodies may be self-accelerated in same direction.

•We examine the self-accelerated motion of equivalent two-mass chain in experiment.

•We show that the Hamilton’s principle is applicable when the energy of the negative mass unit is properly characterized.

A R T I C L E I N F O

Article history:

Accepted 24 August 2015

Available online 15 September 2015

Control

Mass–spring system

Negative effective mass

Dynamics

Self-accelerated

Energy principle

We investigate the interaction between a positive mass and a negative effective mass through a threemass chain connected with elastic springs,a pair of masses is designed to have an effective negative mass,and it interacts with the third positive one as if an equivalent two-mass chain.The dynamics of the equivalent two-mass chain shows thatthe two bodies may be self-accelerated in same direction when the effective mass becomes negative,the experiment is also conducted to demonstrate this type of motion. We furthershow thatthe energy principle(Hamilton’s principle)is applicable ifthe energy ofthe negative mass unit is properly characterized.The result may be relevant to composite with cells of effective negative mass,their interaction with matrix may lead to more richer unexpected macroscopic responses.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).

Dynamics of two bodies connected by a linear spring,predicted by Newton’s second and third laws,may be more diverse than that observed in our daily life,i.e.,the only breathing-like vibration mode of the two bodies.The other predicted possible motion like self-acceleration in the same direction is strictly forbidden due to the requirementon positivity ofmass and stiffness.Hypothetically, the diametric drive,i.e.,two bodies are self-accelerated in the same direction being considered as a possible mechanism of space propulsion,is possible only if one mass becomes negative[1] (here the case of negative stiffness is not considered,although it is also possible).It is known that composite material endowed with microstructure may manifest effectively as a body with a negative effective mass[2–4]or even with an anisotropic mass density[5,6]in some frequency ranges.These composites with unusual physical property are now termed as metamaterials,they were recognized as rapid development in the last decade[7–10]. The metamaterial technique may provide a platform to investigate the phenomena related to negative mass,as already being done for example negative effective mass for wave blocking[11,12],zero effective mass for complete transmission withoutphase change[3] and many others.These phenomena are only discussed with homogenized metamaterials,here we want to go a step further by examining the interaction between a positive mass and a negative (effective)one,which is also relevant to composites with inclusion of negative mass.To this end,we should first realize a negative effective mass and then examine its interaction with a positive one. The first experimental investigation of this kind is conducted by Wimmer et al.[13],they examined the interaction of two photons through a junction formed by two optic fiber loops of different sizes,the phenomenon ofthe diametric drive acceleration isclearly demonstrated.

In this letter,we will investigate the interaction of a positive mass and a negative one through a simple mass–spring system. The idea is the following:we consider a three-mass chain,one adjacent pair of the masses is designed to behave as a body withequivalent negative mass,and the third positive mass interacts with this equivalent negative mass through an elastic spring.Both theoretical analysis and experiment are performed to illustrate the possible motion mode of the diametric drive.We will also examine whether Hamilton’s principle still holds for a system with an effective negative mass concept.

Consider a three-mass chain,as shown in Fig.1(a),both the mass miand stiffness kj(i=0,1,2 and j=1,2)are positive.The mass 2 is connected with the mass 1,underharmonic motion,these two masses may be considered as an effective mass connected to the mass 0,as shown in Fig.1(b).

Using Newton’s second law,the equations of motion for the three masses are written respectively as

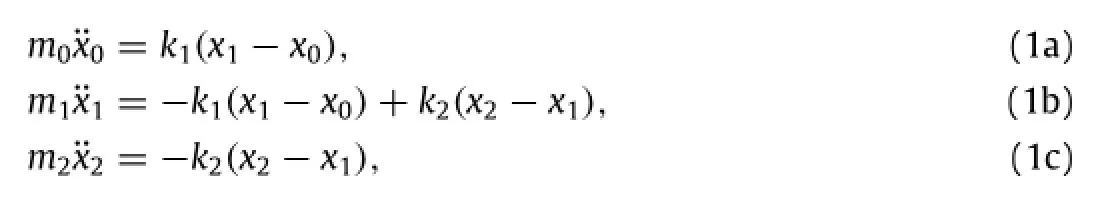
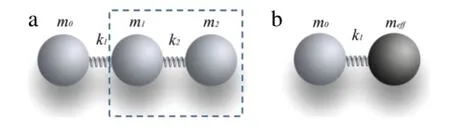
Fig.1.A three-mass chain(a)and its equivalent two-mass system(b).

where xi(t)is the displacement of the mass i.If we consider a steady harmonic motion e−iωtand consider m2as a hidden mass, we eliminate x2from the equations,this leads to

Eqs.(2a)and(2b)are exactly the same for a two-mass system, i.e.,m0and meffare connected by the spring k1.Therefore we can tune the frequencyωto let meff＜0,and examine in turn its interaction with the positive mass m0.For a general two-mass system with one negative mass,Newton’s second law tells that depending on the absolute value ofthe negative mass,the systemwilloscillate if it is larger than the positive one and accelerate in one direction otherwise.For the system shown in Fig.1,it has two natural frequencies,satisfying the following equation

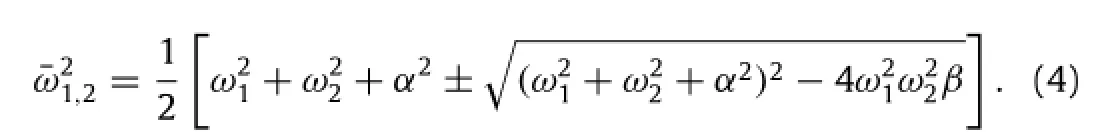
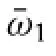
It is well known that the equation of motion for a multi-body system can also be derived from Hamilton’s energy principle,so the question to be addressed in the following is whether the same principle applies if the effective mass becomes negative.

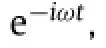
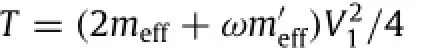
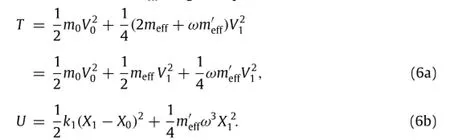
Lagrangian of the system is now written as

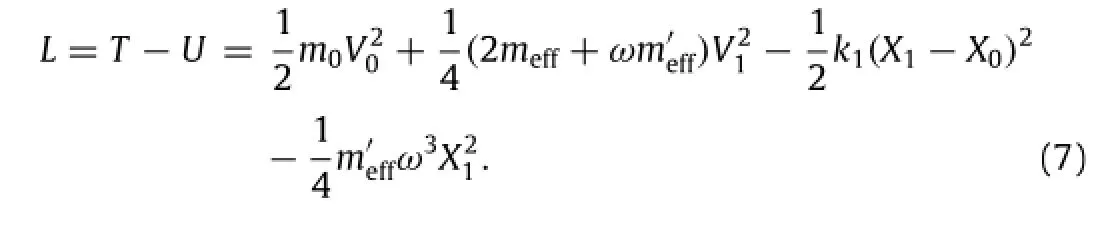
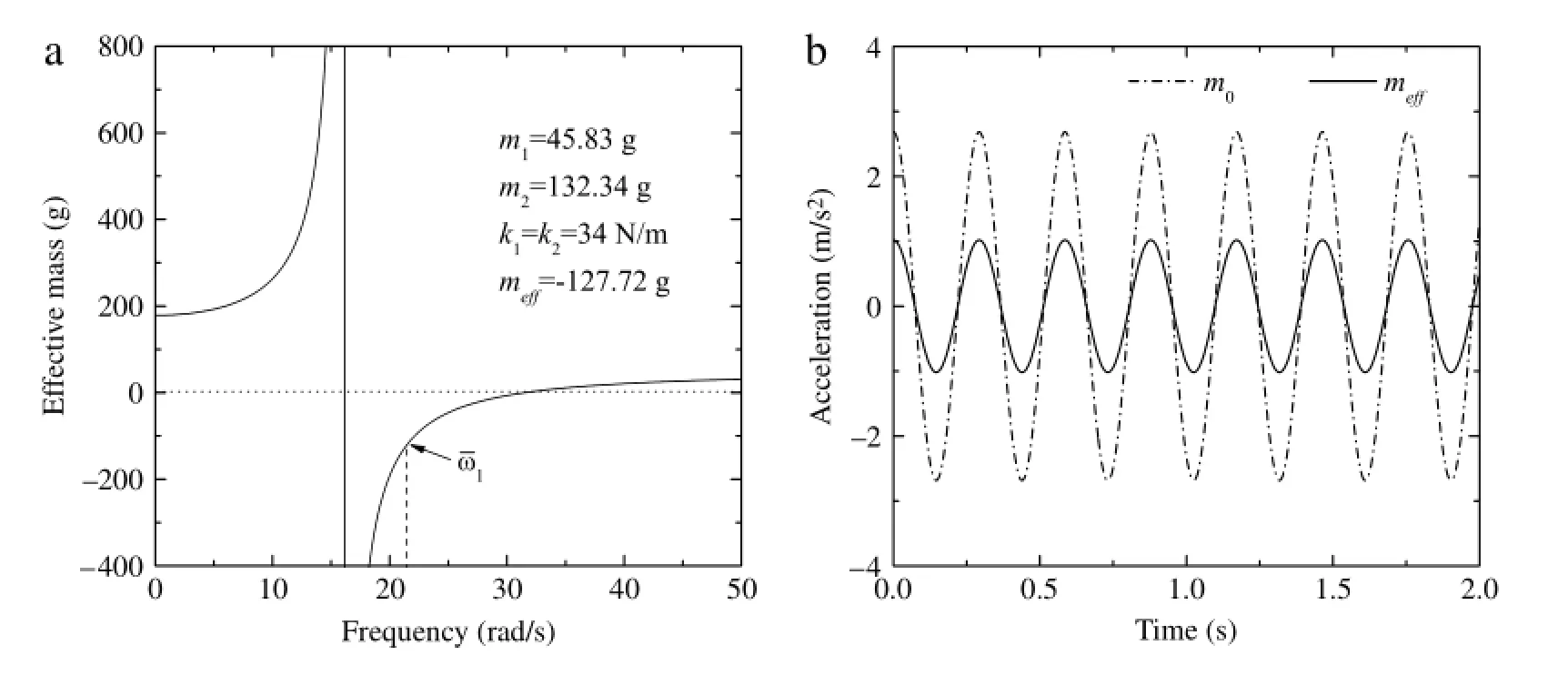
Fig.2.(a)Effective mass of the mass-pair as function of frequency;(b)acceleration of the masses m0,meffas function of time.

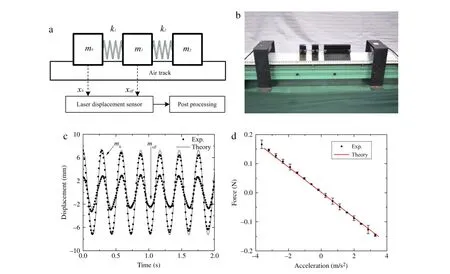
Fig.3.Experimental measurement:(a)principle;(b)experimental set-up;(c)measured and predicted displacements of m0and meffas function of time at¯ω1;(d)measured and predicted force via acceleration on meff.

In the frequency domain,Lagrange equation with Fourier transformation becomes

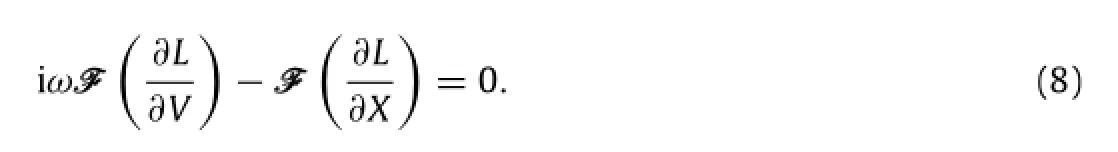
We have for the mass m0and the mass meff

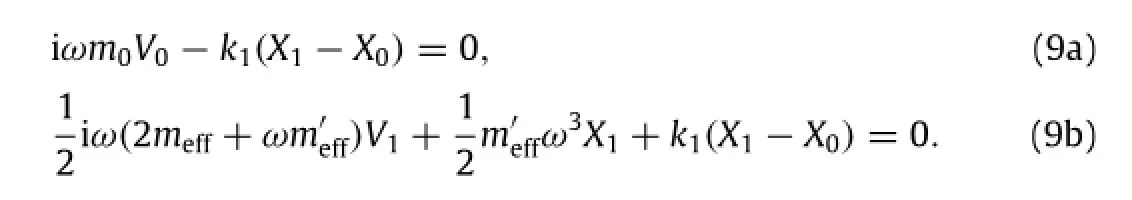
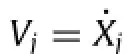
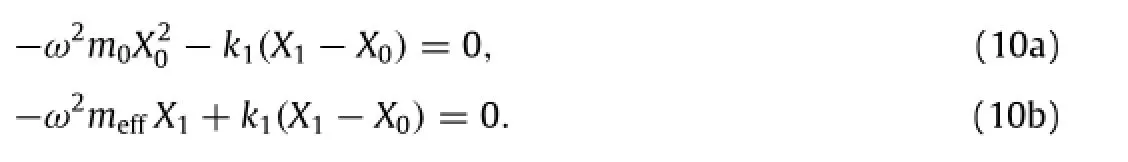
These equations are exactthe same as those derived from Newton’s second law of motion for a two-mass system with one effective mass meff,which may be negative.Therefore if a system with a negative mass unit,the equation of motion can be derived directly from energy principle as usual if the energy of the negative mass unit is correctly interpreted.

In summary,we demonstrate through a three-mass chain that acceleration in same direction of two bodies connected by an elastic spring may take place if one possesses a negative effectivemass.The works may shield light to design some particular composites with inclusions of negative effective mass.

Acknowledgment

This work was supported by the National Natural Science Foundation of China(Grant Nos.11290153 and 11221202).

References

[1]M.G.Millis,Challenge to create the space drive,J.Propul.Power 13(1997) 577–582.

[2]Z.Y.Liu,X.X.Zhang,Y.W.Mao,et al.,Locally resonant sonic materials,Science 289(2000)1734–1736.

[3]S.S.Yao,X.M.Zhou,G.K.Hu,Experimental study on negative effective mass in a 1D mass–spring system,New J.Phys.10(2008)043020.

[4]S.H.Lee,C.M.Park,Y.M.Seo,et al.,Acoustic metamaterial with negative density,Phys.Lett.A 373(2009)4464–4469.

[5]G.W.Milton,J.R.Willis,On modifications of Newton’s second law and linear continuum elastodynamics,Proc.R.Soc.A Math.Phys.Eng.Sci.463(2007) 855–880.

[6]R.Zhu,X.N.Liu,G.K.Hu,et al.,Negative refraction of elastic waves at the deep-subwavelength scale in a single-phase metamaterial,Nature Commun. 5(2014)5510.

[7]R.Zhu,X.N.Liu,G.L.Huang,et al.,Microstructural design and experimental validation of elastic metamaterial plates with anisotropic mass density,Phys. Rev.B.86(2012)144307.

[8]D.Torrent,J.Sanchez-Dehesa,Anisotropic mass density by radially periodic fluid structures,Phys.Rev.Lett.105(2010)174301.

[9]B.I.Popa,S.A.Cummer,Non-reciprocal and highly nonlinear active acoustic metamaterials,Nature Commun.5(2014)3398.

[10]X.Chen,X.C.Xu,S.G.Ai,et al.,Active acoustic metamaterials with tunable effective mass density by gradient magnetic fields,Appl.Phys.Lett.105(2014) 071913.

[11]S.S.Yao,P.Li,X.M.Zhou,et al.,Sound reduction by metamaterial-based acoustic enclosure,AIP Adv.4(2014)124306.

[12]J.Mei,G.Ma,M.Yang,et al.,Dark acoustic metamaterials as super absorbers for low-frequency sound,Nature Commun.3(2012)756.

[13]M.Wimmer,A.Regensburger,C.Bersch,et al.,Optical diametric drive acceleration through action–reaction symmetry breaking,Nat.Phys.9(2013) 780–784.

[14]Y.I.Bobrovnitskii,Energy characteristics of oscillatory systems with internal (h idden) degrees of freedom, Acoust. Phys. 59 (2013) 1–5.

1 July 2015

∗.

E-mail address:hugeng@bit.edu.cn(G.Hu).

http://dx.doi.org/10.1016/j.taml.2015.08.003

2095-0349/©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*This article belongs to the Dynamics and