On the magnetic anomaly at Easter Island during the 2010 Chile tsunami

Benlong Wng∗,Xioyu Guo,Hu LiuCheng Gong

aDepartment of Engineering Mechanics,800 Dongchuan Road,Shanghai 200240,China

bMinistry of Education Key Laboratory of Hydrodynamics,800 Dongchuan Road,Shanghai 200240,China

cChinese Aviation Radio and Electronic Research Institute(CARERI),Shanghai 200233,China

On the magnetic anomaly at Easter Island during the 2010 Chile tsunami

Benlong Wanga,b,∗,Xiaoyu Guoa,Hua Liua,b,Cheng Gongc

aDepartment of Engineering Mechanics,800 Dongchuan Road,Shanghai 200240,China

bMinistry of Education Key Laboratory of Hydrodynamics,800 Dongchuan Road,Shanghai 200240,China

cChinese Aviation Radio and Electronic Research Institute(CARERI),Shanghai 200233,China

A R T I C L E I N F O

Article history:

Accepted 10 August 2015

Available online 8 September 2015

Magnetic anomaly

Tsunami

Nonlinear shallow water equations

A magnetic anomaly was recorded at Easter Island on 27 February 2010 during the Chile tsunami event. The physics of the magnetic anomaly is analyzed using kinematic dynamo theory.Using a single wave model,the space and time behavior of the magnetic field is given.By joint analysis of the magnetic observations,tide gauge data and numerical results of the global tsunami propagation,we show the close resemblance between the predicted spatial and temporal magnetic distributions and the field data, indicating the magnetic anomaly at Easter Island was actually induced by the motion of seawater under tsunamiwaves.Similarity between the field magnetic data atEaster Island during 2010 Chile tsunamiand sea surface level is verified with realistic tsunami propagating model.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).

2010 Chile earthquake occurred off the coast of central Chile on February 27,2010,at 06:34 UTC,having a magnitude of 8.8 on the moment magnitude scale.Large tsunami was generated and propagated across the south Pacific ocean.A tiny magnetic signal oscillation was captured by the magnetic station named IPM after UTC 11:30 am when the tsunami wave passed through Easter Island as shown in Fig.1.The occurrence of oscillation of magnetic field is coincident with the arriving time of tsunami wave,which suggests the tight connection between the seawater’s motion and variation of magnetic field variation.

Magnetic anomaly induced by seawater’s motion is recognized and known in very early days[1–3].Seawater is an electrically conducting media which generates small electromagnetic fields as it flows through the Earth’s main magnetic field.Gravity surface water wave is a common flow form in ocean.Around O(0.1)–O(1)nT magnetic field can be generated by the Kelvin waves after submarine and surface ship at cruise speed[4,5]. Electromagnetic fields tend to enhance when wave periods and lengths increase.Waves of period 16–17 s and amplitude of 1 m can induce magnetic anomaly of 1 nT.Swells of period 10–20 s can induced a magnetic field of 103–104times of the one’s induced by wind waves of 5 s.Typical tide flow can induce magnetic field of 20–30 nT.For some internal wave in tropical area,measured magnetic fields value may reach 100 nT[6].Tyler[7]compared and found similarities between the results of a numerical prediction of lunar M2tide(i.e.twice tide cycles in one day)and scalar magnetic records measured by satellite CHAMP.It has been shown for the first time that the ocean flow makes a substantial contribution to the geomagnetic field at satellite altitude.For the magnetic anomaly induced by 2010 Chile tsunami,it is the first time that field magnetic data induced by seawater’s motion under tsunami was captured.However,the shifted sea surface record at Deepocean Assessment and Reporting of Tsunamis(DART)51406 with a time lag were imperfectly used to verify the existence of the similarity due to the lack of accurate seismic data[8,9].

Employing global tsunami transport modeling,at now we can simulate the sea surface elevation during the 2010 tsunami event accurately.We start with modeling the sea surface elevation during the selected tsunami events,employing the phase resolved global tsunami propagation equations.A benchmarked numerical package GeoClaw[10],an adaptive numerical solver of nonlinear shallow water equations in spherical coordinates,was used to simulate the 2010 Chile tsunami propagation across the south Pacific ocean,which has been successfully used on 2004 Sumatra tsunami and 2012 Tohoku tsunami[11].ETOPO 2-min global dataset at the National Geophysical Data Center(NGDC)is used for the bathymetry in offshore region at a resolution of 10 min in latitude and longitude,and 1-min dataset is used near the epicenter. Initial sea surface deformation was computed by applying Okada’sformulas for 180 sub-fault using the fault parameter[12].With the refined adaptive mesh,good agreements at DART 32412 and 51406 are obtained as shown in Fig.2.Although there is no DART data at Easter Island,we have confidence that the numerical results of GeoClaw could predict reliable sea surface elevation since the position IPMlocates between DART 32412 and 51406 along the tsunami’s path.On a mild slope bathymetry,leading waves from shoaling of a transient wave usually appear like a capital letter N or M[13,14].In the same situation,numerical wave gauges from GeoClawrecord similar tsunamishapes as shown in Fig.2 when the tsunami approaching Easter Island.However,a single wave profile was captured by DART buoy,where the water is deep and there is no wave shoaling effects.Snapshots of sea surface elevation during the tsunami event are given in Fig.3.

As shown in Fig.2,the numerical model nearly perfectly captures the period and amplitude ofthe firstwave at site DART 51406. The simulated tsunamiarrived approximately 6 min before the observed tsunami.Such a phase shift has been previously discussed and corresponds to the dispersive effects ofnaturaltsunamiwaves. However,the nonlinear shallow-water equations used in present simulations neglect dispersive effects and therefore over-predict the phase speed.From the linear frequency dispersion relation,the phase speed of tsunami waves can be estimated by

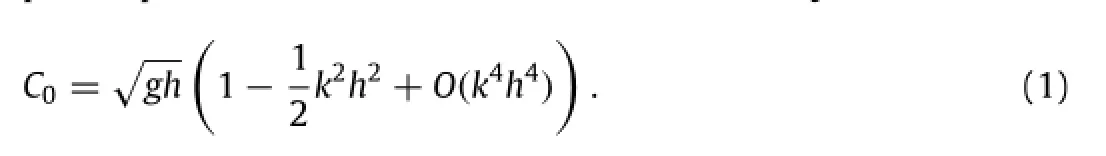
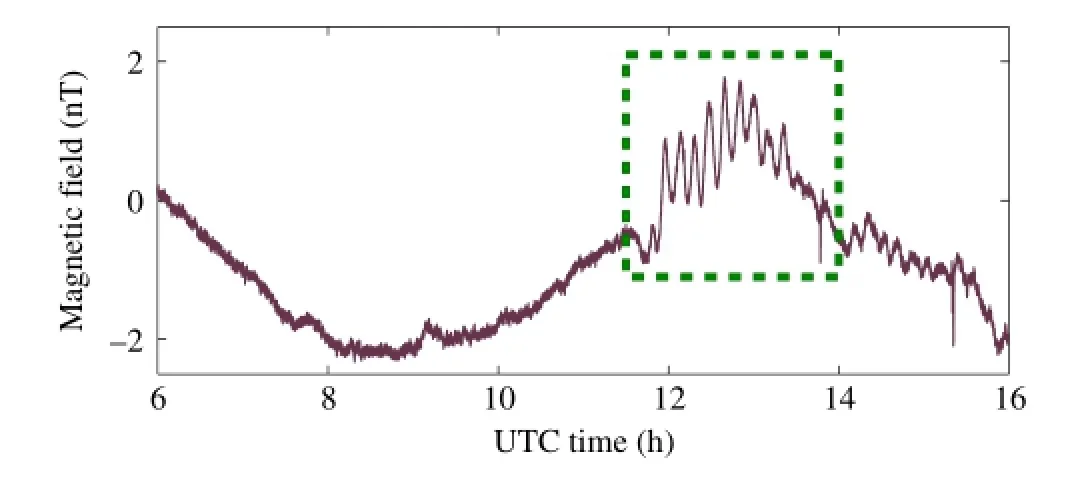
Fig. 1. Vertical component of total main magnetic field at IPM during February 27, 2010 Chile tsunami event. Mean value of -19000 nT has been subtracted. Magnetic gauge station IPM is operated by the Bureau Central de Magnetisme Terrestre, France, locates at (−27.200° S, −109.420° W).

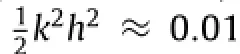
At DART 32412,the main feature of the sea surface elevation is captured.The slight discrepancy is attributed to the interaction of large-scale resonance from the coast to the edge of the continental shelf.With validation using data from the two DART gauges, the numerical tsunami propagation model provides a reliable sea surface elevation for the leading wave near Easter Island.The trailing tsunami waves near Easter Island,however,cannot be well predicted by nonlinear shallow-water equations due to the weak dispersive properties.Therefore,the magnetic field induced by the trailing waves is excluded from our analysis.

Generation of magnetic field by a conductive fluid’s motion is known as the dynamo problem.The complete dynamo problem consists of the equations of motion and Maxwell equations,which are coupled by the action of the Lorentz forces.Due to the tiny magnetic strength caused by seawater’s motion,the Lorentz forces exerted on seawater can be neglected,which lead to an equilibrium magnetic field.Therefore the hydrodynamic problem and dynamo problem are decoupled.Using kinematic dynamo theory,the induced magnetic field could be predicted when the seawater velocity is known.

Harmonic solutions of linear kinematic dynamo problem for linear progressive waves were obtained by many works[2,3]. Focusing in the tsunami induced magnetic field,two kinds of one dimensional simplified models are derived:the first one is based on the projection of Maxwell equation at vertical direction[15]; taken the dispersive effects into account an elaborated model was proposed recently[9].The attenuation of the induced magnetic field could be well predicted by these two models for long waves. At sea surface,both of these two models reduce to a simple formulae:the induced magnetic field linearly depends on the sea surface elevation.The other relative parameters include the local main magnetic field,the local water depth and conductivity of the seawater.

When considering the induced magnetic field at the sea surface only,the dispersive model and long-wave approximation reduce to the same expression for long waves:

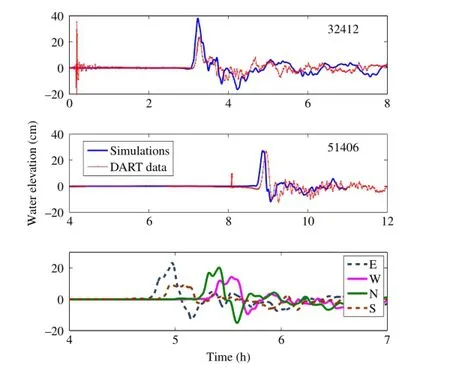
Fig.2.Sea surface elevation during February 27,2010 Chile tsunami event.DART 51406 and 32412 are two buoysforrealtime tsunamimonitoring systems operated by National Oceanic and Atmospheric Administration(NOAA)center for tsunami research.Sea surface elevations at four numericalwave gauges around Easter Island, wherein E,W,N and S are abbreviation of each directions.These four positions are two degrees away from Easter Island.

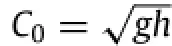
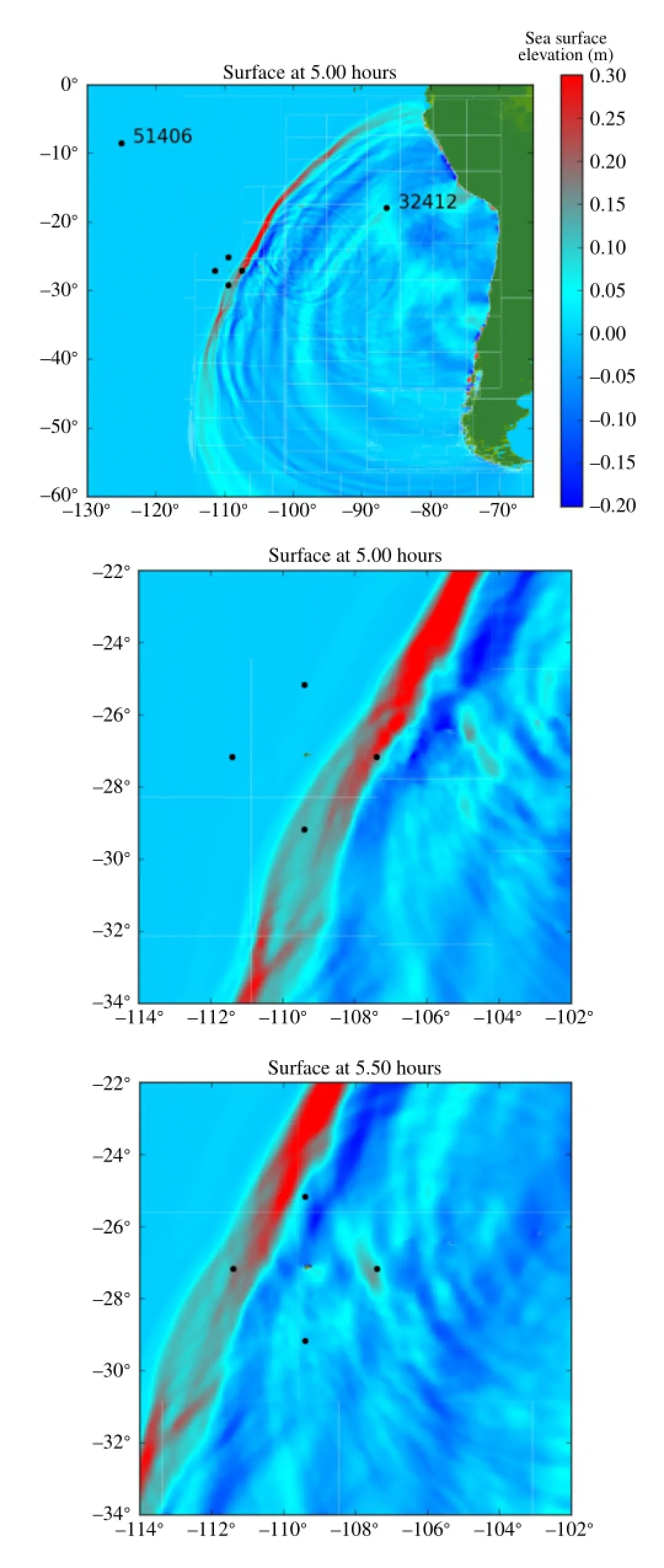
Fig.3.Top:sea surface elevation at 5.0 h of origin earthquake time.DART 51406 and 32412 are two buoys for real time tsunami monitoring systems operated by NOAA center for tsunami research.Middle and bottom:sea surface elevations at four numerical wave gauges around Easter Island,wherein E,W,N, and S are abbreviation of each directions.The horizontal and vertical coordinates are longitude and latitude respectively,and the color represents the sea surface elevation in meters.These four positions are two degrees away from Easter Island. (For interpretation of the references to color in this figure legend,the reader is referred to the web version of this article.)

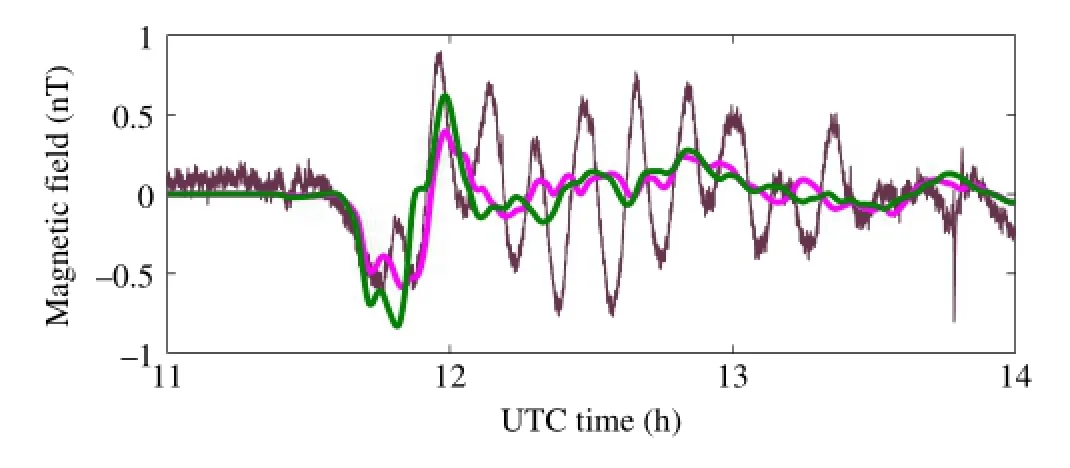
Fig.4.Predicted and observed amplitude are almost congruent.The north and west numerical wave gauges information are used to estimate the magnetic field, due to the bathymetry effects are fully developed when the tsunami passed by the island.The slow variation of main Earth magnetic field is filtered.In the trailing part after 12 o’clock,the short dispersive tsunami waves are not be accurately predicted with nonlinear shallow water equations.Consequently,the periodic variation of magnetic signal could not be predicted.

The space–time behavior of magnetic anomalies induced by tsunamis in open oceans has been investigated.It was found that the magnitude of the magnetic anomaly induced by a 0.2 m tsunami is on the order of 1.0 nT at the sea surface.Even using a simple 1D kinematic dynamo model,the induced magnetic field is well predicted,see Fig.4,which indicating the essence of the phenomenon is well captured.

Focusing on tsunami waves,it has been verified in a very real sense that the seawater’s motion induced an observable magnetic field,although it is a tiny signal comparing with the background main Earth magnetic field.This has important implications:a small amplitude transoceanic tsunami is expected to be on time detected before it propagates into shallow water region,which may serve as a makeup especially at regions such as Indian Ocean and South China Sea,where tsunami monitoring systems have not been setup yet but high risk is identified for the next devastating tsunami[16].In broader terms,it encourages future studies on the multidiscipline interactions associated with tsunami as well as other kinds of long waves in ocean.Based on the spatial and temporal behaviors of the magnetic signal over the ocean surface, seawater’s motions of certain scales are expected to be detected remotely by unmanned near space airship or satellite[7,17],which may provide novel approaches for scientific research.

Acknowledgments

We thank Keller Stroke from NOAA for providing 2010 Chile tsunami wave elevation at DART 32412 and 51406.The geomagnetic data are obtained from the Bureau Central de magnetisme Terrestre(http://www.bcmt.fr).Supports by the Shanghai Leading Academic Discipline Project(No.B206)and National Natural Science Foundation of China(No.11272210)are greatly appreciated.

References

[1]M.Faraday,Experimentalresearches in electricity,Philos.Trans.R.Soc.London 122(1832)163–177.

[2]J.T.Weaver,Magnetic variations associated with ocean waves and swells, J.Geophys.Res.70(1965)1921–1929.

[3]J.C.Larsen,The electromagnetic field of long and intermediate water waves, J.Mar.Res.29(1971)28–45.

[4]D.Madurasinghe,E.O.Tuck,The induced electromagnetic field associated with submerged moving bodies in an unstratified conducting fluid,IEEE J.Ocean. Eng.19(1994)193–199.

[5]N.Zou,A.Nehorai,Detection of ship wakes using an airborne magnetic transducer,IEEE Trans.Geosci.Remote Sens.38(2000)532–539.

[6]L.D.Pukhtyar,A.S.Kukushkin,Investigation of the electromagnetic fields induced by sea wave motion,Phys.Oceanogr.7(1996)33–41.

[7]R.Tyler,S.Maus,H.Luhr,Satellite observationsofmagnetic fields due to ocean tidal flow,Science 299(2003)239–241.

[8]C.S.Manoj,S.Maus,A.Chulliat,Observation of magnetic fields generated by Tsunamis,EOS Trans.Am.Geophys.Union 92(2011) http://dx.doi.org/10.1029/2011EO020002.

[9]B.Wang,H.Liu,Space–time behavior of magnetic anomalies included by tsunami waves in open ocean,Proc.R.Soc.A 469(2013)20130038.

[10]http://depts.washington.edu/clawpack/users/geoclaw.html.

[11]R.J.LeVeque,D.L.George,High-resolution finite volume methods for the shallow water equations with bathymetry and dry states,in:P.L.F.Liu,H.Yeh, C.E.Synolakis(Eds.),Advanced Numerical Models for Simulating Tsunami Waves and Runup,World Scientific,2008,pp.43–73.

[12]R.J.LeVeque,D.L.George,M.J.Berger,Tsunamimodelling with adaptive refined finite volume methods,Acta Numer.20(2011)211–289. http://dx.doi.org/10.1017/S0962492911000043.

[13]S.Tadepalli,C.E.Synolakis,The run-up of N-waves on sloping beaches,Proc.R. Soc.Lond.Ser.A 445(1994)99–112.

[14] P.A. Madsen, D.R. Fuhrman, H.A. Schäffer, On the solitary waveparadigm for tsunamis, J. Geophys. Res. 113 (2008) 1–22.

[15] R. Tyler, A simple formula for estimating the magnetic fields generated by tsunami flow,Geophys.Res.Lett.32(2005)L09608. http://dx.doi.org/10.1029/2005GL022429.

[16]P.L.F.Liu,X.Wang,A.J.Salisbury,Tsunami hazard and early warning system in South China Sea,J.Asian Earth Sci.36(2009)2–12.

[17] S. Maus, F. Yin, H. Lühr, e t a l ., Resolution of direction of oceanic magnetic lineations by the six-generation lithospheric magnetic field model from CHAMP satellite magnetic measurements,Geochem.Geophys.Geosyst.9 (2008)Q07021.

3 August 2015

∗ at: Department of Engineering Mechanics, Shanghai Jiao Dongchuan Roa, Shanghai 200240, China.

E-mail address:benlongwang@sjtu.edu.cn(B.Wang).

http://dx.doi.org/10.1016/j.taml.2015.08.001

2095-0349/©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*This article belongs to the Fluid Mechanics