Direct comparison of hydraulic tortuosity and electric tortuosity based on finite element analysis

H.Saomoto∗,J.Katagiri

aInstitute of Earthquake and Volcano Geology,National Institute of Advanced Industrial Science and Technology,Tsukuba,Ibaraki,305-8567,Japan

bMethane Hydrate Research Center,National Institute of Advanced Industrial Science and Technology,Tsukuba,Ibaraki,305-8569,Japan

Direct comparison of hydraulic tortuosity and electric tortuosity based on finite element analysis

H.Saomotoa,∗,J.Katagirib

aInstitute of Earthquake and Volcano Geology,National Institute of Advanced Industrial Science and Technology,Tsukuba,Ibaraki,305-8567,Japan

bMethane Hydrate Research Center,National Institute of Advanced Industrial Science and Technology,Tsukuba,Ibaraki,305-8569,Japan

A R T I C L EI N F O

Article history:

2 June 2015

Accepted 24 June 2015

Available online 21 July 2015

Hydraulic tortuosity

Electric tortuosity

Porous media

Porosity

Finite element method

Tortuosity is one of the key parameters to characterize the transport properties of porous media.There are many models for tortuosity estimation based on some definitions:geometric,hydraulic,electric,and diffusive definitions.However,relationships among those tortuosities remain unclear due to the lack ofdirect comparison on the same porous media.Here we focus on hydraulic and electric tortuosities and have conducted a series of finite element simulations with the Navier–Stokes equation and the equation for electric current to directly compare tortuosities.The results revealed that:(1)on average,hydraulic tortuosity is 15%greater than that ofthe electric one;(2)the proposed modelbased on the van Genuchten-type function successfully approximates both hydraulic and electric tortuosities;(3)tortuosities obtained from the porous media packed with circular particles and square particles show quantitatively similar trends.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY license(http://creativecommons.org/ licenses/by/4.0/).

Tortuosity is one of the key parameters to represent complex microstructure in porous media and much affects the macroscopic transport properties characterized by parameters such as permeability,electric conductivity,and diffusion conductivity.For instance,permeability derived from the Kozeny–Carman equation[1]is expressed as a function of porosity,shape factor,and tortuosity.Also,Archie’s law[2],which is an experimental model for electric conductivity of porous media,incorporates the effect of tortuosity by a parameter referred to as tortuosity factor.

There are many models for tortuosity estimation based on some definitions[3,4]:geometric models[5,6](Tg),hydraulic models [7,8](Th),electric models[9,10](Te),and diffusive models[11,12] (T]d).Those models are different in terms of their basic concepts: geometry,fluid mechanics,electrodynamics,and diffusion equation.However,it should be noted that most of those models for each tortuosity are a function of porosity despite of the difference between the background concepts.Besides,the magnitude relation among those tortuosities is considered to hold Tg＜Td≈Te＜Thfrom the viewpoint of dimensional analysis for the local hydraulic and electric conductivities at a point on a flow path[13–15].However,the relationships among those magnitude are quite qualitative and remain unclear due to the lack of direct comparison on the same porous media.One of the few investigations of the comparison for hydraulic and electric tortuosities is demonstrated by Ghanbarian et al.[4]using the Wheatstone bridge circuit,but it seems difficult to model complicated pore structure with a single Wheatstone bridge.

Here we focus on the differences between hydraulic and electric tortuosities and have conducted a series of finite element simulations to directly compare hydraulic and electric tortuosities on the same finite element mesh.Using the simulation results, we have discussed the relation between hydraulic and electric tortuosities and have newly proposed an empirical model for both tortuosities.Note that it is difficult to experimentally measure the tortuosity inside the porous media.

Figure 1 shows the porous models used in this study.Here, two series of porous media are prepared:one is composed of circular particles having the diameter of 2.0 mm(Fig.1(a)),the other is composed of square particles having the edge length of 1.772 mm(Fig.1(b)).Since it is known that tortuosity depends on the value of porosity,we produced several porosity levels ranging from 0.5 to 0.9 by means of the Monte Carlo computation without intersection of each particle.Next,we need to solve two types of partial differential equations defined on those porous models to obtain tortuosities;one is for porous flow and the other is for electric current.

The governing equation of porous flow is the stationary Navier–Stokes equation described as follows:

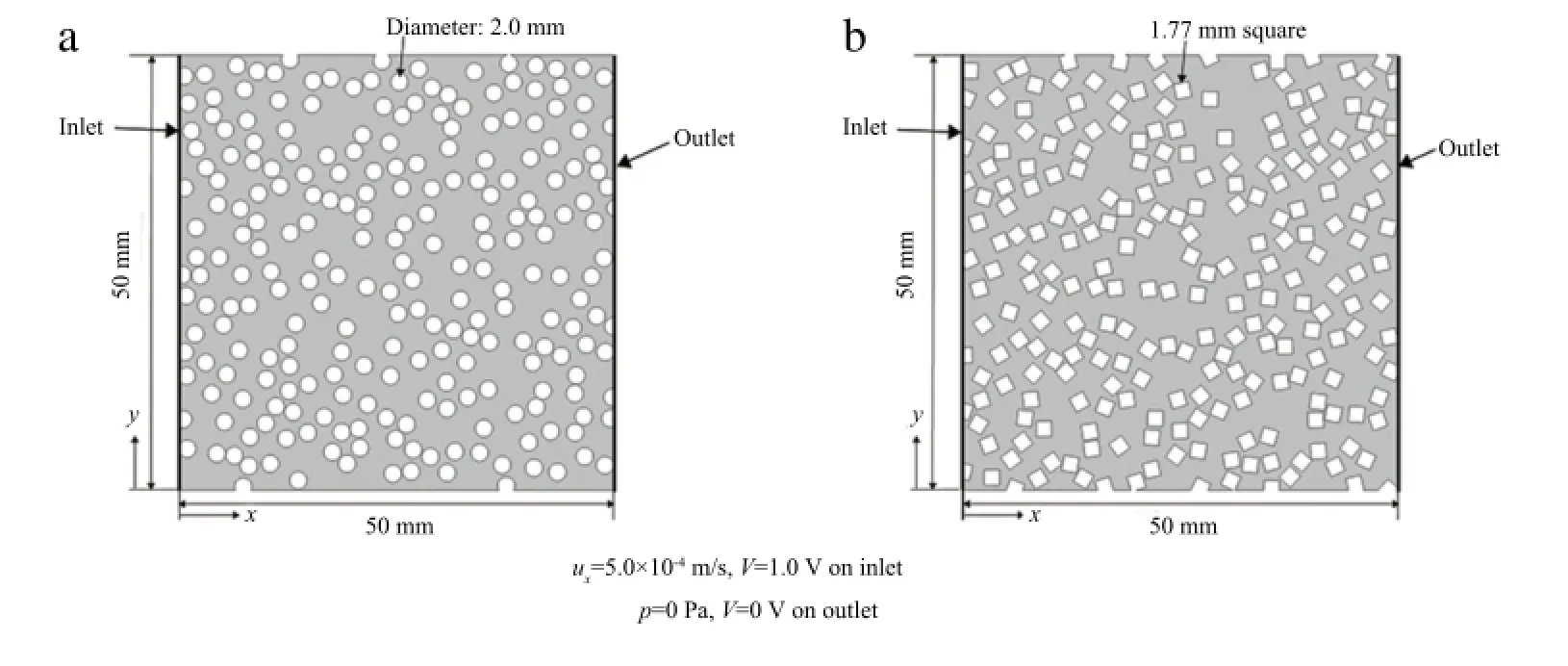
Fig.1.(a)Porous media composed of circular particles having diameter of 2.0 mm(porosity:0.70).(b)Porous media composed of square particles having edge length of 1.772 mm(porosity:0.70).

Table 1Physical properties of pore fluid.

where u,ρ,p,andµare velocity of the pore fluid,density of the pore fluid,pore pressure,and the viscosity of the pore fluid,respectively.Physical parameters of the pore fluid,which is assumed to be water,are listed in Table 1.The no-slip boundary condition(u=0)is adopted at the solid boundaries in the porous media.The constant normal fluid velocity(5.0×10−4m/s)is set at the inlet,which satisfies a condition concerning the Reynolds number(Re)expressed by Re=1.The pressure free boundary is set at the outlet(p=0).The other governing equation for stationary electric current is given as follows:

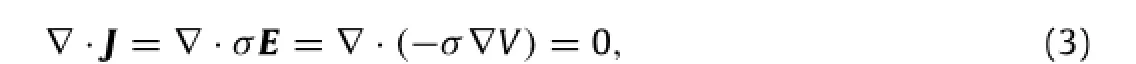
where V,E,J,andσare electric voltage,electric field,current density,and the electric conductivity of the pore fluid,respectively. The insulated boundary conditions(n·J=0)are applied on the edges ofthe solid region exceptthe boundaries where electric voltage is defined.Electric voltages at the boundaries are set to 1.0 V for the inlet and to 0 V for the outlet,respectively.

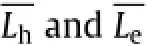
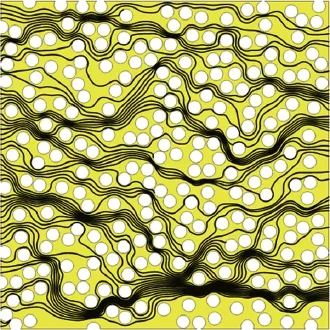
Fig.2.Streamlines of hydraulic flow(porosity:0.70).

Fig.3.Streamlines of electric flow(porosity:0.70).

Figures 2 and 3 respectively show hydraulic and electric streamlines for the porous media having porosity of 0.7 withcircular particles.As can be seen in Fig.2,some localized flow paths are clearly produced,in which relatively higher fluid velocities are observed.In contrast to the result of the hydraulic streamlines, electric streamlines(Fig.3)seem to be quite homogeneous. It is emphasized that these tendencies were always observed irrespective of the particle shapes and porosity.To understand those phenomena,the dimensional analyses for hydraulic and electric conductivities are useful.Friedman and Seaton[13] derived proportional relations for those conductivities via the dimensional analyses such that gh∝r4and ge∝r2,where ghand gedenote hydraulic and electric conductivities,respectively. Also,r indicates the radius of a cylinder regarded as a part of fluid path.Since various sizes of r will be found in the porous media, the heterogeneity of those conductivities will arise.We can thus easily comprehend that the higher exponent of r leads to strong heterogeneity,which results in highly tortuous streamlines.

Figure 4 shows the relationship between tortuosities and the porosity for the circle packed porous model,in which five different cases were simulated at each porosity level.Note that the variance of tortuosities among five cases is simply caused by the five different pore structures.We can find some features.(1)In a large sense,both hydraulic and electric tortuosities have linearity with respect to porosity.(2)The ratio Th/Tereaches almost 1.2 when porosity equals 0.5.(3)The variance among five cases at a porosity for hydraulic tortuosity is higher than that of the electric one. Yazdchi et al.[16]simulated almost the same problem of porous flow with circular particle packed porous model and they also indicated the linear relationship for the hydraulic tortuosity,which is nearly identical to our results.Nevertheless,the linear relation seems difficult to hold the fundamental boundary condition: Th(or Te)→∞atφ=0,Th(or Te)→1 atφ=1,whereφ represents porosity.

Now we discuss the relationship between our numerical results and the models for both hydraulic and electric tortuosities considered as a function of porosity.One of the most used models for the estimation of both hydraulic and electric tortuosities(T)is the logarithmic function of porosity[7,11,17–20],which is given by

where P is a parameter to be determined by experiments or simulations.Evidently,the logarithmic function satisfies T→∞at φ=0 and T→1.0 atφ=1.According to Comiti and Renaud[7],the value of P for hydraulic tortuosity ranges from 0.86 to 3.2 for plate-packed porous media with different particle aspect ratio.For two dimensional porous flow problem,Matyka et al.[19] derived P=0.77 for the hydraulic tortuosity from the lattice Boltzmann simulation for a porous modelcomposed offreely overlapping squares.We also fitted our results by Eq.(5)and found good agreements with P=0.50 for the hydraulic tortuosity and with P=0.20 for the electric tortuosity(Fig.4).Presence of overlapping particles in the porous media is thought to be the major cause of the difference between our fitted result and the result reported by Matyka et al.[19].In other words,the aggregated particles are easily apt to generate long flow channels due to their large diameter,resulting in a larger value of P.Itshould be noted that the logarithmic function cannot precisely trace the higher porosity region(φ≥0.7)of the hydraulic tortuosity due to the tangent trend being convex upward.In fact,this convexed tendency of the hydraulic tortuosity is commonly observed in most of simulation results[16,19,21].On the other hand,the electric tortuosity is clearly approximated by the logarithmic function.

To improve the accuracy of the fitting with the boundary conditions and the convexed region mentioned above,we newly propose a function to evaluate the tortuosity based on the van Genuchten-type function[22].That is,

Fig.4.Relationship between tortuosities and porosity for circular particle packed porous media.

Fig.5.Relationship between tortuosities and porosity for square particle packed porous media.

whereα(positive value)and m(0≤m≤1)are fitting parameters. As the van Genuchten function is originally designed for moisture characteristic curve of soils having the changing tangent,it is suitable for locally convexed trend as indicated in the hydraulic tortuosity.Although there are two parameters,geometric meanings of those are quite clear;parameterαregulates the location of the inflection pointon the curve and parameter m controls the increasing trend of the curve.Also,the proposed model may be simple to use because the parameter m is a normalized parameter.The upper and lower bounds for the parameters are important when we determine the parameters via the non-linear least square fitting. Usingα=0.217 and m=0.572,the proposed function well approximates the plot of hydraulic tortuosity distributed within 0.5≤φ≤0.9(Fig.4).In addition to hydraulic tortuosity,the proposed function can also fit the plot of the electric tortuosity with a high degree of accuracy.

Figure 5 shows the relationship between tortuosity and porosity for the square particle packed porous media.Similarly, the proposed model can also fit both tortuosities precisely.By comparing Fig.4 with Fig.5,we can discuss the effect of particle shape to tortuosities.According to the regression equationproposed by Comiti and Renaud[7],they argued that a higher aspect ratio leads to a higher value of P.Since the difference in the aspect ratio between a circle and a square is small,similar tortuosity trends are formed in each model.

The knowledge obtained from this study is summarized as follows. (1) In two-dimensional problem, the ratio composed of hydraulic and electric tortuosities (Th/Te) is less than 1.2 with φ≥ 0.5. (2) The logarithmic function fails to fit hydraulic tortuosity in the higher porosity region (φ ≥ 0.7) due to the tangent trend be-ing convex upward. (3) We proposed an empirical model to es-timate both hydraulic and electric tortuosities based on the van Genuchten-type function. The model successfully approximates tortuosities distributed within 0.5 ≤ φ ≤ 0.9. (4) Both the logarithmic function and our model clearly approximate the electric tortuosity. (5) Tortuosities obtained from the porous media packed with circular particles and square particles show similar trends, suggesting that the particles with high aspect ratio will be required to discuss the shape effect to tortuosity.

Future work on our tortuosity model is to estimate the applicability of the proposed model based on the van Genuchtentype function to the three-dimensional porous model composed of realistic irregular-shaped particles such as sand grains.

References

[1]P.C.Carman,Fluid flow through granular beds,Trans.Inst.Chem.Eng.15 (1937)150–166.

[2]G.E.Archie,The electrical resistivity log as an aid in determining some reservoir characteristics,Pet.Trans.AIME 146(1942)54–62.

[3]M.B.Clennell,Tortuosity:a guide through the maze,Geol.Soc.Lond.Spec.Publ. 122(1997)299–344.http://dx.doi.org/10.1144/GSL.SP.1997.122.01.18.

[4]B.Ghanbarian,A.G.Hunt,R.P.Ewing,et al.,Tortuosity in porous media:a critical review,Soil Sci.Soc.Am.J.77(2013)1461–1477. http://dx.doi.org/10.2136/sssaj2012.0435.

[5]B.-M.Yu,J.-H.Li,A geometry model for tortuosity of flow path in porous media,Chin.Phys.Lett.21(2004)1569–1571.http://dx.doi.org/10.1088/0256-307X/21/8/044.

[6]P.-Y.Lanfrey,Z.V.Kuzeljevic,M.P.Dudukovic,Tortuosity model for fixed beds randomly packed with identical particles,Chem.Eng.Sci.65(2010) 1891–1896.http://dx.doi.org/10.1016/j.ces.2009.11.011.

[7]J.Comiti,M.Renaud,A new modelfordetermining mean structure parameters of fixed beds from pressure drop measurements:application to beds packed with parallelepipedal particles,Chem.Eng.Sci.44(1989)1539–1545. http://dx.doi.org/10.1016/0009-2509(89)80031-4.

[8]M.Mota,J.A.Teixeira,W.R.Bowen,et al.,Binary spherical particle mixed beds:porosity and permeability relationship measurement,Trans.Filtr.Soc. 44(2001)101–106.

[9]J.C.Maxwell,A Treatise on Electricity and Magnetism,vol.1,Clarendon Press, London,1873.

[10]S.W.Coleman,J.C.Vassilicos,Transport properties of saturated and unsaturated porous fractal materials,Phys.Rev.Lett.100(2008)035504. http://dx.doi.org/10.1103/PhysRevLett.100.035504.

[11]H.L.Weissberg,Effective diffusion coefficient in porous media,J.Appl.Phys. 34(1963)2636–2639.

[12]J.W.Beeckman,Mathematical description of heterogeneous materials, Chem.Eng.Sci.45(1990)2603–2610.http://dx.doi.org/10.1016/0009-2509(90)80148-8.

[13]S.P.Friedman,N.A.Seaton,Critical path analysis of the relationship between permeability and electrical conductivity of three-dimensional pore networks, Water Resour.Res.45(1998)1703–1710. http://dx.doi.org/10.1029/98WR00939.

[14]A.G.Hunt,Applications ofpercolation theory to porous media with distributed local conductances,Adv.Water Resour.24(2001)279–307. http://dx.doi.org/10.1016/S0309-1708(00)00058-0.

[15]R.P.Ewing,A.G.Hunt,Dependence of the electrical concuctivity on saturation in real porous media,Vadose Zone J.5(2006)731–741. http://dx.doi.org/10.2136/vzj2005.0107.

[16]K.Yazdchi,S.Srivastava,S.Luding,On the validity of the Carman–Kozeny equation in random fibrous media,in:Internatinal Conference on Particlebased Methods II,PARTICLES 2011,October 26–28,Barcelona,Spain,2011.

[17]D.S.Tsai,W.Strieder,Effective conductivities ofrandom fiber beds,Chem.Eng. Commun.40(1986)207–218. http://dx.doi.org/10.1080/00986448608911698.

[18]E.Mauret,M.Renaud,Transport phenomena in multi-particle systems—I. Limits of applicability of capillary model in high voidage beds-application to fixed beds of fibers and fluidized beds of spheres,Chem.Eng.Sci.52(1997) 1807–1817.http://dx.doi.org/10.1016/S0009-2509(96)00499-X.

[19]M.Matyka,A.Khalili,Z.Koza,Tortuosity-porosity relation in porous media flow,Phys.Rev.E 78(2008)026306. http://dx.doi.org/10.1103/PhysRevE.78.026306.

[20]M.Barrande,R.Bouchet,R.Denoyel,Tortuosity ofporous particles,Anal.Chem. 79(2007)9115–9121.http://dx.doi.org/10.1021/ac071377r.

[21]A.Duda,Z.Koza,M.Matyka,Hydraulic tortuosity in arbitrary porous media flow,Phys.Rev.E 84(2011)036319. http://dx.doi.org/10.1103/PhysRevE.84.036319.

[22]M.Th.van Genuchten,A closed-form equation for predicting the hydraulic conductivity of unsaturated soils,Soil Sci.Soc.Am.J.44(1980)892–898. http://dx.doi.org/10.2136/sssaj1980.03615995004400050002x.

1 September 2014

in revised form

∗.

E-mail address:h-saomoto@aist.go.jp(H.Saomoto).

http://dx.doi.org/10.1016/j.taml.2015.07.001

2095-0349/©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY license(http://creativecommons.org/licenses/by/4.0/).

*This article belongs to the Fluid Mechanics