地下集水工程渗滤系统的离散元数值模拟

齐 阳，高 强，唐新军，李晓庆

(新疆农业大学 水利与土木工程学院，新疆 乌鲁木齐830052)

地下集水技术是利用所营造的渗滤系统(河床含水层+人工滤层 +集水构筑物)的滤净功能，将地表江河水及含水层潜水诱渗至集水构筑物内并取出地表的一种取水技术[1]。该方法是新疆农村安全饮水以及工农业用水的常用取水方式之一。但是目前该技术缺乏系统、完善的研究，有关层间系数的合理取值范围缺乏明确的规定，造成集水工程滤层设计的随机性比较大，极易出现渗滤系统淤堵或者基土细粒大量穿过滤层进入集水廊道的问题[2]。

然而，目前地下集水工程渗滤系统的研究大多停留在宏观角度，难以从本质上揭示其渗滤机理。渗滤系统的研究问题属于典型的流固耦合问题，目前众多学者[3－11]在解决流固耦合问题时多采用颗粒流的方法。周健等[3]采用颗粒流的方法在砂土管涌——滤层防治方面进行了模拟研究;李识博等[4]对松散堆积物坝基渗透淤堵试验进行颗粒流模拟;倪小东[5]采用颗粒流的方法模拟了管涌的砂槽试验。上述数值模拟试验结果与相关物理试验结果均拟合较好，充分说明了颗粒流方法解决流固耦合问题的可行性。因此，本文尝试采用颗粒流的方法对均匀基土－滤层渗滤系统进行不同层间系数(D15/d85，其中 D15、d85分别为滤料、基土的控制粒径)的系列数值模拟试验，以验证颗粒流方法在地下集水工程渗滤系统研究方面的可行性，以便用其对复杂级配基土做更深一步的研究。

1 基土－滤层渗滤系统数值模拟原理

1.1 流固方程

对于固相颗粒，通常采用力－位移定理和动量方程[12]来模拟颗粒的运动。

对于液相介质，采用 Navier－Stokes连续方程和运动方程[13]模拟孔隙中流体的运动，具体如下式所示:

式中:ρf为流体密度;ε为孔隙率;v为流速;εv为宏观流速;t为时间;▽为梯度;▽p为压力梯度;μ为流体的动力黏度;fb为单位体积内流体与颗粒之间的作用力，主要为流体与固体之间的拖曳力，可用下式表示:

估算孔隙介质渗透性的公式有很多，但其核心都是Kozeny－Carman关系式，这里采用渗透率公式[14]估算渗滤系统各层的渗透性:

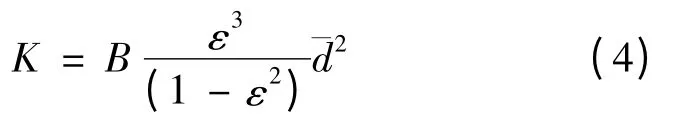
式中:B为常数，其值常取1/180;ε为孔隙率;¯d为颗粒平均直径。

1.2 流固耦合过程

颗粒流程序中，流固耦合方程采用显示差分方程求解。当前时步根据颗粒间位置按力－位移定理确定接触力，并将该力与流体对颗粒的拖曳力叠加后根据运动方程确定下一时步颗粒新位置、速度及接触力。流体采用划分网格法计算，流域内颗粒运动引起孔隙率变化，从而造成渗透率、流速等改变，进而影响到流体对颗粒的拖曳力，继而影响颗粒下一时步的位置，具体过程如图1所示。

图1 颗粒流流固耦合计算过程

2 基土－滤层渗滤系统数值模型的建立

本文采用Cu小于5的砂样作为基土，并根据层间系数比(D15/d85)的需要更改滤料控制粒径生成试样。本次数值模拟试验设定的层间系数有3、3.5、4、4.5、5、6 六个值，因此涉及到的滤料也为六种。基土和滤料的级配曲线如图2所示。

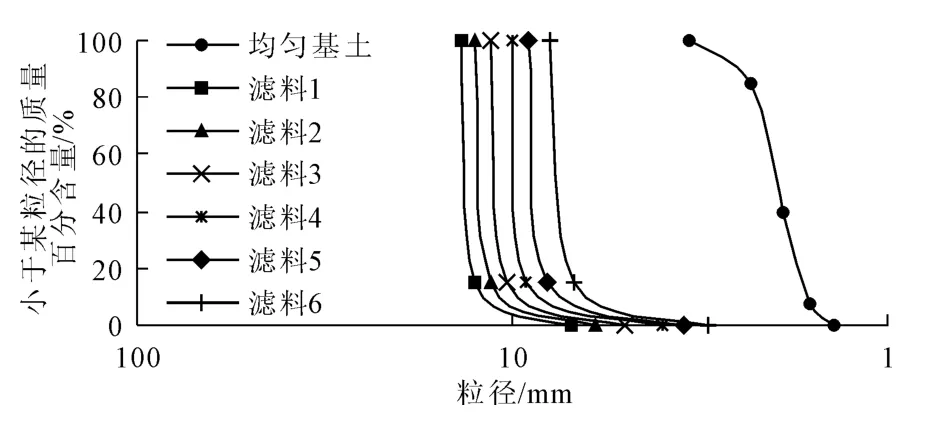
图2 基土及其滤料级配曲线

综合考虑基土细粒含量、计算机运行速度限制等因素后，将数值模型的尺寸定为60 mm×60 mm×100 mm。数值模型中，X、Y轴向墙不能透水，主要作用是限制颗粒侧向移动;Z轴负半轴墙，边界条件设定为可透水，Z轴正半轴墙为网状墙，其作用等效于允许水流和颗粒穿过的边界条件。流体单元的尺寸定为12 mm×12 mm×10 mm，试样部分占据5×5×10个单元，如图3灰色网格线所示。模型中，基土和滤料分别占总空间的2/5和3/5。数值模型及模型参数分别见图3和表1。

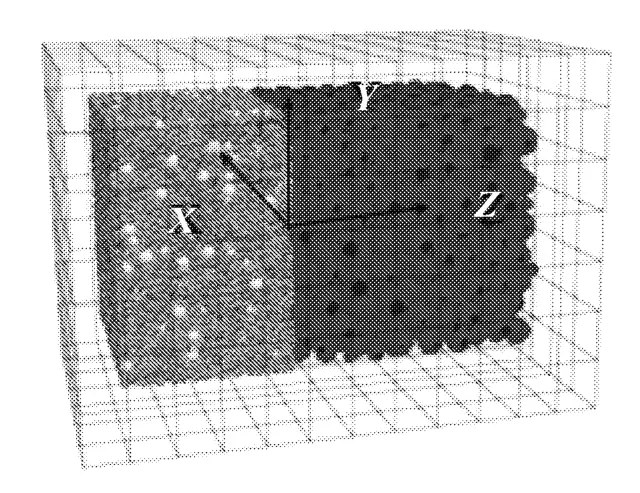
图3 数值模型

表1 数值模型参数

模型最小尺寸 60 mm，基土最大粒径为 3.4 mm，滤料最大粒径是8 mm～13.65 mm，模型最小尺寸与基土、滤料最大粒径的比值分别为17.65、4.39 ～7.5，符合相关试验标准[15]中不得小于 4 的规定。为防止基土、滤料颗粒在生成过程中剧烈混掺，生成一墙将模型沿Z轴方向分成两个空间，在左侧空间生成基料，循环消除内部不均衡力后，再在右侧空间生成滤料，再经过循环消除不均衡力后，删除中间墙体。最后，在Z轴向砂样两端施加20 kPa的压力差(确保水力梯度远大于发生管涌的临界水力梯度)，并保持右端压力为零，使砂样沿Z轴向产生一定的压力梯度，模拟实际情况下的沿重力方向的渗流。

3 模拟结果分析

利用流体单元参数及程序内置FISH语言设置监测函数，获取基土中心、滤层及两者界面处的孔隙率、渗透率的变化情况，统计基土流失率、侵蚀率及滤层各处基土颗粒的滞留情况，以探究系统水力特性变化规律。基土沿Z轴方向平均分成10层，将第3层和第5层分别作为基土和界面的监测层，滤层的参数取6～10层的均值。基土层间系数D15/d85表示滤层设计准则，D15为滤料控制粒径，d85为基土控制粒径。

3.1 不同层间系数对应的渗滤系统中基土颗粒的移动状态

图4给出了不同层间系数情况下模拟试验结束时数值模型中颗粒的分布情况。其中，每个层间系数同时给出隐去滤料颗粒和不隐去滤料颗粒时数值模型中的颗粒分布状态。

图4 不同D15/d85值下模拟试验结束时渗滤系统中基土颗粒的分布状态

由图4可知，当 D15/d85不大于3.5的时候，基土颗粒无明显整体移动，极少量的基土细粒进入并滞留在滤层靠近界面处;当 D15/d85介于4～5之间的时候，基土颗粒出现明显的整体移动，主要体现在，界面处基土颗粒进入滤层之后，上游基土颗粒整体向下移动填充界面处位置，出现不同程度的沉降;当D15/d85大于5的时候，形成集中的渗流通道，基土颗粒沿渗流通道持续移动，逐渐发展成管涌破坏。

总体而言，对于均匀基料，渗流过程中颗粒的移动规律主要表现为沿着渗流方向整体移动，渗透变形表现为较大的沉降变形。这主要是由均匀基料的级配决定的，均匀基料没有骨架颗粒和填充颗粒之分，所有颗粒都参与骨架结构的形成，基土颗粒间孔隙较细，且较细颗粒和较粗颗粒粒径相差不大，所以不存在细颗粒沿粗颗粒孔隙移动的现象，因此当界面处颗粒进入滤层之后，上游颗粒就会整体向下移动。

3.2 不同D15/d85值下渗滤系统各处孔隙率的变化

图5给出了不同层间系数下渗滤系统基土、滤层及两者界面处的孔隙率随渗流作用时间的变化曲线。六种情况下，滤层的孔隙率皆先递减然后再保持稳定。但是，随着D15/d85值的增加滤层的孔隙率的减小量加大，这是因为D15/d85值越大，滤料越粗，

图5 基土、滤层及两者界面处的孔隙率随渗流作用时间的变化曲线

进入滤层的基土颗粒就愈多，孔隙率就愈小。基土中心和界面处的孔隙率都是先增加后保持稳定，并且D15/d85越小，保持稳定的速度越快。但是对于滤层的孔隙率，层间系数较大的时候，渗流初期波动较剧烈，这是因为D15/d85较大时有较多的基土颗粒穿过界面进入滤层，因此在系统稳定之前孔隙率处于波动状态。整体而言，当D15/d85≤5时，渗滤系统各处孔隙率最终趋于稳定，说明上述渗滤系统最终都保持稳定，不会发展成管涌。此外，模拟试验结束时，界面处孔隙率明显大于基土和滤层，且不随渗流作用时间减小，充分说明该情形下均匀基料不会出现在界面处淤堵的情形;当层间系数大于5时，界面处的孔隙率持续减小，说明模拟试验结束时渗滤系统仍处于不稳定状态。

3.3 不同D15/d85值下渗滤系统各处渗透率的变化

图6、图7分别给出了不同层间系数下渗滤系统中基土、界面处的渗透率，滤层的渗透率随渗流作用时间的变化曲线。由渗透率的计算公式可知，渗透率的大小主要与孔隙率和监测范围内的颗粒平均粒径有关。对于均匀基料，由于没有细料迁移现象，

孔隙率不会有太大变动，又由于基土中心和界面处颗粒平均粒径相差不大，所以该情况下，基土渗透率K基和界面处渗透率K界的变化曲线与孔隙率的变化曲线接近。由于界面处有颗粒较大的滤料颗粒，平均粒径会大于基土中心处，因此对于任一D15/d85值皆有K界＞K基。

6种情况下，滤层的渗透率都是先递减后保持稳定。初始渗透率随着D15/d85的增加而增大，但是稳定后的渗透率随着D15/d85的增加而减小，甚至会出现低于界面处的情况。这主要是由于D15/d85值较小的时候，基土颗粒难以或者少量进入滤层，滤层保持了较大的渗透率，但是 D15/d85值较大时，大量基土颗粒进入滤层造成滤层孔隙率和颗粒平均粒径显著降低，致使渗透率显著下降。

由上述分析可知，对于均匀基料，当 D15/d85的取值能够保持渗滤系统稳定的时候，始终有K基＜K界＜K滤，但是在层间系数大于5的时候，由于滤层滞留的基土颗粒过多，会出现渗透性低于界面处的情况，应予以避免。

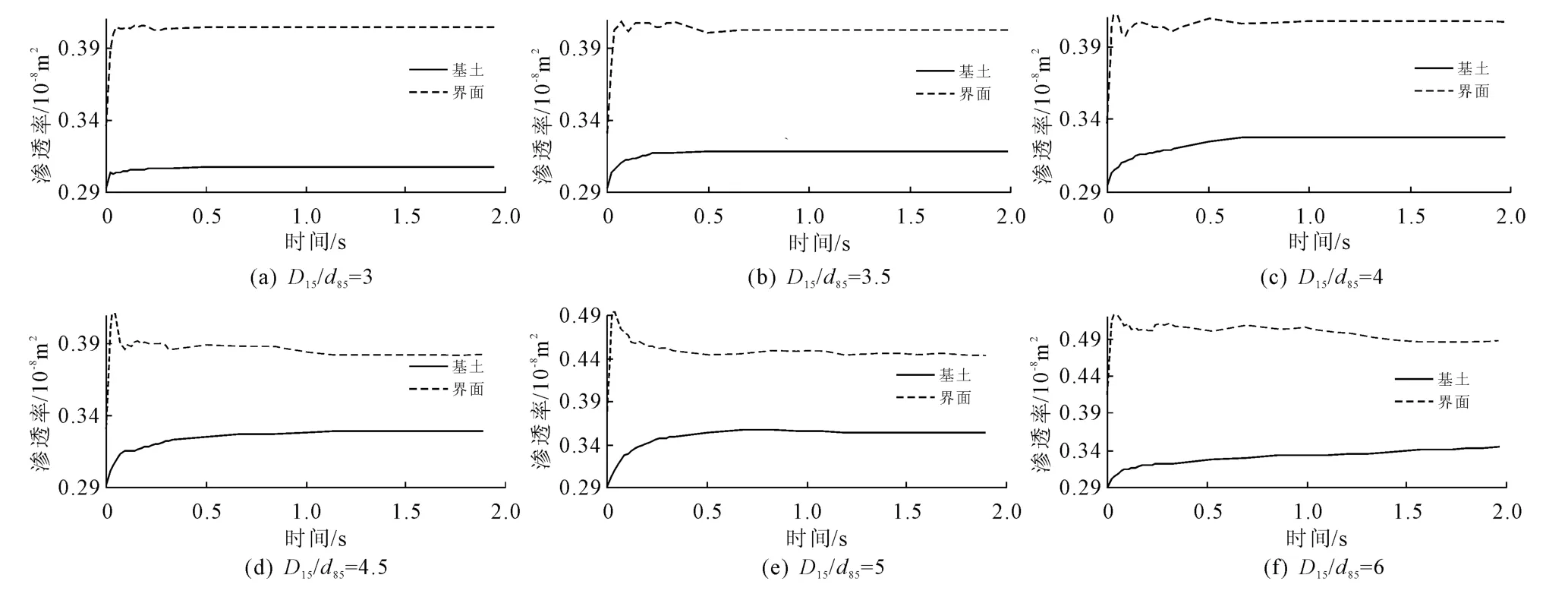
图6 基土、界面处的渗透率随渗流作用时间的变化曲线

3.4 不同D15/d85值下渗滤系统滤层各处侵蚀基土颗粒量的变化

将数值模型滤层部分沿渗流方向平均分成三层(根据靠近基土的程度，依次为第一层、第二层、第三层)，统计出各层的侵蚀基土颗粒的总体积随渗流作用时间的变化情况，以便分析不同时刻滤层各层侵蚀基土颗粒的分布情况，如图8所示。由图8可知，进入滤层的基土颗粒主要滞留在第一层，并随着D15/d85的增加，呈现逐渐增多的趋势;第二、三层滞留的基土颗粒量很少，随 D15/d85的增加略微增大，但D15/d85＞5时，呈现显著增加的趋势。

由此可知，D15/d85≤5时，进入滤层的基土颗粒通常会滞留在滤层中，但这时由于进入滤层的颗粒总量较少不会造成滤层淤堵;D15/d85稍大于5时，由于滤层第一层滞留的基土颗粒过多，会造成滤层出现明显淤堵的现象。

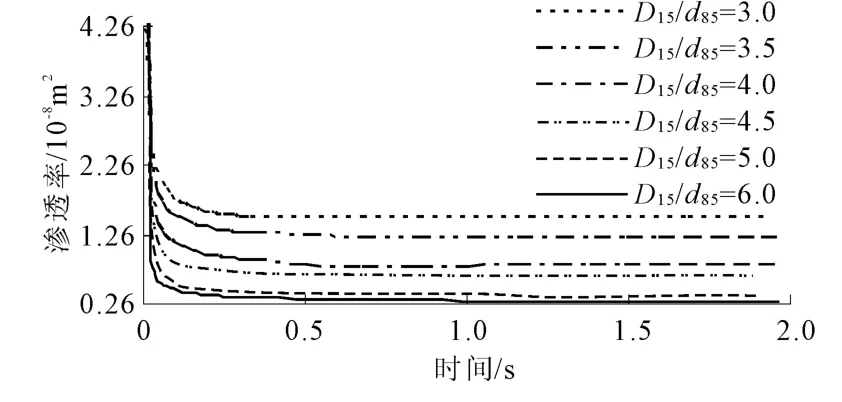
图7 不同层间系数下滤层的渗透率随渗流作用时间的变化曲线

图8 不同D15/d85值下滤层各分层侵蚀基土颗粒量的变化曲线

3.5 不同D15/d85值下进入滤层和穿出滤层的基土百分量的变化

图9 、图10分别给出了不同层间系数下进入滤层的基土百分量和穿出滤层的基土百分量随渗流作用时间的变化曲线，其中进入滤层的基土量又称为侵蚀基土量。从图9、图10中可以明显看出，对于均匀级配基土，在层间系数小于或者等于5的情况下进入滤层的侵蚀基土颗粒量曲线最终都趋于水平，并且穿出滤层的侵蚀基土百分量亦趋于平缓，且保持在一个较小的范围内，说明在该层间系数范围内，渗滤系统最终会趋于稳定，不会发展成为管涌;层间系数大于5时，进入滤层的侵蚀基土颗粒量和穿出滤层的侵蚀基土量在渗流后期仍处于增长的趋势，且模拟结束时侵蚀基土量已达到了16%，穿出滤层的侵蚀基土量也已经是层间系数不大于5时的数倍，因此势必会发生较大的沉降变形，所以认为该情况下系统不稳定。

图9 进入滤层的基土百分量变化曲线

图10 穿出滤层的基土百分量变化曲线

综合上述分析可知，对于均匀级配基土，在设定的水力梯度下，对系统的保土性分析后发现，D15/d85≤5时，渗滤系统流失的颗粒较少，滤层的保土功能良好;D15/d85＞5时，渗滤系统会流失较多的基土颗粒，形成较大的沉降变形，滤层的保土功能较差，渗滤系统濒临失稳的边缘。该结果与太沙基准则基本一致，说明采用颗粒流的方法对基土－滤层渗滤系统进行数值模拟研究是可行的。对系统的透水性分析后发现，D15/d85在3～5之间时，系统始终有K基＜K界＜K滤，渗滤系统透水功能良好。对滤层侵蚀基土颗粒的滞留情况分析后发现，随着D15/d85的增加，侵蚀基土量递增，但D15/d85≤5时，由于进入滤层的侵蚀基土量有限不会造成滤层淤堵。

4 结论

(1)颗粒流方法，在基土－滤层渗滤系统模拟方面具有独到的优势，它不仅可以对各粒径区间颗粒的移动过程进行直观的观测，还可以监测渗滤系统各处的孔隙率、渗透率，基土流失百分量等参数的变化过程，从而实现对渗滤系统的精准分析。

(2)层间系数D15/d85的取值是决定滤层是否有效及渗滤系统水力特性优劣的主要因素，当D15/d85≤5时，渗滤系统保土功能和透水功能都比较好;当D15/d85＞5时，渗滤系统保土功能不足，有集中渗漏通道形成，系统失稳。由此可知，对于地下集水工程中的滤层，若含水层为均匀基土，宜控制层间系数D15/d85不大于5。

(3)数值试验结果与太沙基准则的一致性，充分说明了采用颗粒流的方法对基土－滤层渗滤系统进行数值模拟研究是可行的，结果是可信的，值得用其对渗滤系统进行更深入的研究。

[1]吴正淮.渗渠取水[M].北京:中国建筑工业出版社，1981.

[2]李晓庆，高 强，唐新军.细沙河道上修建地下集水廊道的工程实践[J].人民长江，2013，44(17):29-32.

[3]周 健，周凯敏，姚志雄，等.砂土管涌 －滤层防治的离散元数值模拟[J].水利学报，2010，41(1):17-24.

[4]李识博，王常明，王刚城，等.松散堆积物坝基渗透淤堵试验及颗粒流模拟[J].水利学报，2012，43(10):1163-1170.

[5]倪小东，王 媛，王 飞.管涌的砂槽试验研究及颗粒流模拟[J].四川大学学报:自然科学版，2009，41(6):51-57.

[6]刘先珊，刘 洋.考虑流固耦合效应的饱和砂土渗流破坏数值模拟[J].兰州大学学报:自然科学版，2013，49(5):633-643.

[7]游碧波，周翠英.双层堤基条件下管涌逸出的颗粒流模拟[J].中山大学学报:自然科学版，2010，49(6):42-49.

[8]郑 刚，戴 轩，张晓双.地下工程漏水漏砂灾害发展过程的试验研究及数值模拟[J].岩石力学与工程学报，2014，33(12):2458-2471.

[9]周 健，姚志雄，张 刚.砂土渗流过程的细观数值模拟[J].岩土工程学报，2007，29(7):977-981.

[11]刘 洋，周 健，付建新.饱和砂土流固耦合细观数值模型及其在液化分析中的应用[J].水利学报，2009，40(2):250-256.

[12]Itasca Consulting Group Inc. PFC3D Version4.0[M].USA:Itasca，2008.

[13]Itasca Consulting Group Inc. PFC3D Particle Flow Code in 3 Dimensions-Optional Features[M]. USA:Minneapolis，2005.

[14]JACOB Bear. Hydraulics of Groundwater[M]. McGrao－ Hill，1979.

[15]中华人民共和国水资源部.SL237－057－1999粗颗粒土的渗透及渗透变形试验[S].北京:中国水利水电出版社，1999.