MPC法在水电站厂房结构数值模拟中的应用研究

2015-12-21王明辉马震岳

水利与建筑工程学报 2015年5期

王明辉，陈婧，马震岳，吴娴

(大连理工大学建设工程学部水利工程学院，辽宁大连116024)

在工程实践中，梁和壳与三维连续实体的组合结构是较为常见的结构方式。例如在进行大型水电站厂房结构分析时，由于整体结构复杂，若全部采用实体单元进行建模，除了前期处理工作量大以及导致生成大量的单元节点外，还需要消耗巨大的计算机资源。对于该类复杂结构的建模，通常拆分为梁、壳单元与实体单元，以达到减小节点数的目的[1]。问题是这三种单元的节点具有不同的自由度，使得不同单元的节点位移不协调[2]，对此通常主要有以下几种处理方案:刚度叠加法、约束方程法和MPC法等[3]。其中MPC法与其他处理方案相比，具有简捷、适应性强、精度高等优点。

杜宝江等通过研究，验证了在静力计算中，MPC法可以代替约束方程法解决实体单元与梁单元的连接问题[4];谢元丕，冯刚通过研究，验证了在静力计算中，MPC法可以替代约束方程法解决实体单元与壳单元的连接问题[5－6]。

MPC法虽在不少结构中进行了应用，并进行了精度验证[7－8]。但目前有关 MPC法的建模研究仅针对一些较为简单的结构或构件，而在水电站厂房这类由蜗壳、尾水管等组成的独特的复杂结构建模中，MPC法的适用性仍有待验证。另外，目前MPC法的应用也仅局限于静力分析中，在动力分析方面的适用性还不得而知。因此，本文尝试将MPC法应用到水电站厂房这类复杂的结构建模及分析中，且分别通过静力、动力两方面的分析，与整体采用实体单元建模的计算结果进行比较，以验证MPC法的有效性和适用性。

1 理论分析

虽然不同自由度的单元相互组合，在构成总刚度矩阵时按单元下标叠加是没有问题的，但是由于不同单元的自由度不同，可能会导致叠加后在某些方向上出现物理自由度不连续、应力不连续等问题的存在。为了解决这个问题，通常会在划分网格时进行一定的处理，使得不同的单元使用同一个节点，这样可以保证节点平动位移的协调性，但是转角位移的协调性仍然有很大的问题。

例如，梁单元的轴线与实体单元表面相互垂直，如图1所示，两种不同的单元在连接处共同使用节点i，对于实体单元来讲，节点 i有三个不同的自由度，如式(1)所示:

式中:u'i，v'i，w'i分别是沿节点局部坐标系(x'，y'，z')坐标轴方向的位移。

对于梁单元来讲，节点i有六个不同的自由度，如式(2)所示:

式中:θ'ix，θ'iy，θ'iz分别为绕节点局部坐标系(x'，y'，z')坐标轴的转角。

虽然三维实体单元①在节点i处不能转动，但是梁单元②在节点i却有三个转角自由度，可以分别绕着三个不同的方向进行转动，形成铰接。如图1所示，梁单元在节点i处能够随意转动[9]，而实际结构并非如此，如果使用这样的模型进行分析，将会产生错误的结果[10]。

图1 实体单元与梁单元共用节点i

2 MPC法

MPC全称为 Multipoint Constraint，即多点约束方程。通过建立协调方程，MPC法可以将没有对应网格处的节点联系在一起[5]，从而保证不同单元节点的协调性，使得计算结果精确可靠。在大型结构分析软件Ansys中，MPC算法主要使用Conta174与Conta175等接触单元[11]。MPC方程的本质是定义不同自由度节点的一种特定的耦合关系，具体来说就是选取某一个节点的一些自由度为标准值，定义其它某几个节点的某几个自由度与标准值的特定关系[12－13]。

MPC法一般关系式如下:

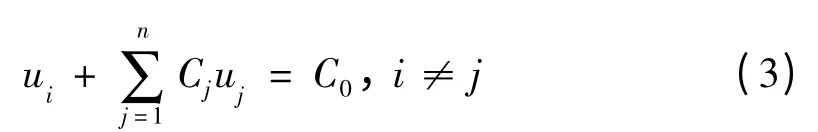
式中:ui为从自由度;uj为主自由度;Cj为权系数;C0为常数项;i，j分别为从、主节点某个自由度的下标号。

通过Ansys软件，可以利用MPC算法对不同自由度单元节点进行连接处理，具体操作主要有以下内容:通过接触单元将不同自由度单元的节点定义为接触关系，选择计算的方法为 MPC，确定接触面的方式为绑定[14－15]。

3 计算模型

本文依据某水电站工程实际结构建立了计算模型。水电站厂房各机组段结构基本相同，机组段中间设结构缝。为了提高计算效率，从中选择一个机组段进行分析研究。计算模型范围从厂房左侧结构分缝处至右侧结构分缝处，从上游边墙至下游边墙，从尾水管底部至发电机层顶部。模拟的结构既包括蜗壳以及其外围混凝土、机墩等大体积混凝土构件，也包括立柱、楼板等局部细小构件。计算模型与实际结构的尺寸比例为1∶1。

在计算模型中建立以Z轴为垂直方向的笛卡尔坐标系，以1 686 m高程(水轮机安装高程)处为原点，向上为正，以X轴和Y轴为水平坐标，以机组中心为原点，X轴与厂房纵向轴线平行，正方向指向左侧;Y轴与厂房纵向轴线垂直，为横向，正方向指向右侧。模型的纵剖面和横剖面分别如图2和图3所示。

3.1 实体模型建模

如图4所示的模型，楼板、立柱、风罩、机墩、蜗壳等全部采用Solid45或Solid95实体单元。模型底部施加三向固定约束，厂房左右岸廊道以上分缝处边界自由，水轮机层以下的其它边界均用弹簧单元Combine14模拟围岩约束边界条件。这个假定全部采用实体单元建模的计算结果是准确的，作为比较的基础。

图2 厂房纵剖面

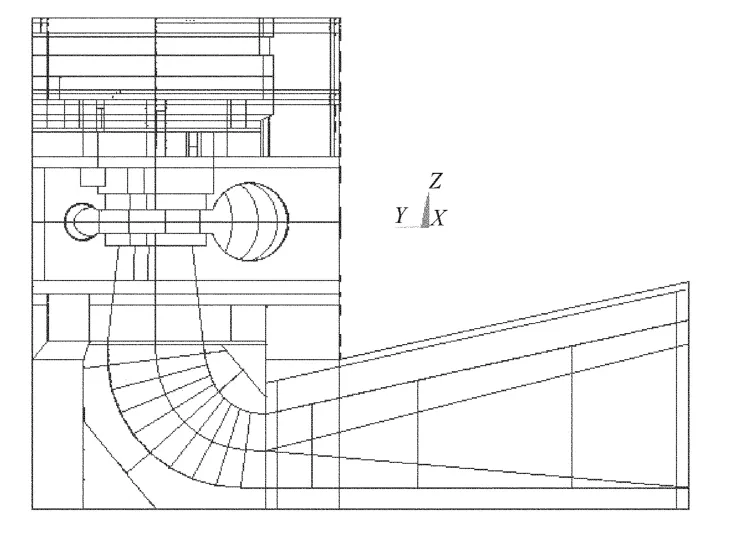
图3 厂房横剖面

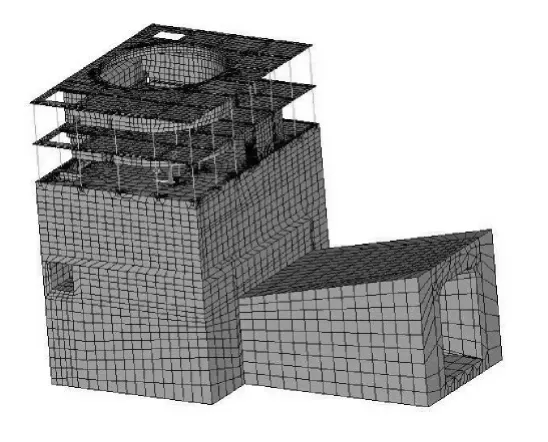
图4 实体计算模型

3.2 梁壳单元与实体单元组合建模

如图5所示的模型，楼板采用壳单元Shell63来模拟，立柱和梁采用 Beam188单元模拟，风罩、机墩、蜗壳等全部采用 Solid45或 Solid95实体单元。模型底部施加三向固定约束，厂房左右岸廊道以上分缝处边界自由，水轮机层以下的其它边界均用弹簧单元Combine14模拟围岩约束边界条件。以此为实体－板壳组合单元计算模型。

图5 梁壳与实体组合计算模型

4 实例分析

4.1 静力计算

机墩组合结构是水电站厂房中关键的受力结构，不仅有着极其复杂的构造，包含有较大较多的孔洞，而且承受着水轮机和发电机等传递的静力荷载和动力荷载。因此规范对水电站厂房机墩刚度有明确的要求，因此有必要对机墩的刚度进行验算分析。分别在定子基础截面和下机架上的节点上施加水平单位力、切向单位力和竖向单位力，以此计算定子基础和下机架的各个方向刚度。得到的定子基础截面和下机架截面的刚度结果列于表1。

表1 两种模型机墩刚度结果对比表

从表1中可以看出，楼板采用壳单元、立柱和梁采用梁单元时，机墩各个部位各个方向的最小刚度均小于厂房结构全部采用实体单元时的对应值，但减小的幅度很小，最大仅减小了1.6%。说明在水电站厂房的静力分析中，MPC法可以有效地解决实体单元与梁单元以及实体单元与壳单元的连接。

4.2 模态计算

分别对实体单元与梁壳实体组合单元模型进行模态计算。得到两种模型机墩的前20阶自振频率，列于表2中;将实体单元模型计算的前3阶阵型列于图6(a)、图7(a)、图8(a)，将梁壳实体组合单元模型计算的前3阶阵型列于图6(b)、图7(b)、图8(b)。

表2 两种模型机墩的前20阶自振频率对比表

从表2中可以看出，楼板采用壳单元、立柱和梁采用梁单元时，机墩部位的频率均小于厂房结构全部采用实体单元时的对应值，最大仅减小了1.7%。从阵型图中可以看出，两种方案的阵型图基本相似。说明在水电站厂房的模态分析中，MPC法可以有效地解决实体单元与梁单元以及实体单元与壳单元的连接。

4.3 谐响应计算

水轮发电机组运行时所产生的振动荷载主要有垂直动荷载、水平动荷载和发电机扭矩。由于静力法计算无法反映振动荷载作用的频率等因素的影响，因此利用动力法进行计算。在动力法计算中，将机组振动荷载作为简谐振动力施加在定子基础和下机架截面处，并且认为各荷载分项是同相位的。由于荷载特性符合谐响应方法的条件，因此可以方便地采用此法进行计算。机墩部位谐响应计算成果如表3所示。

从表3中可以看出，楼板采用壳单元、立柱和梁采用梁单元时，机墩各个部位的位移和应力与厂房结构全部采用实体单元时的对应值相差很小;位移值最大仅相差1.8%，应力值最大仅相差3.4%。说明在水电站厂房的谐响应分析中，MPC法可以有效地解决实体单元与梁单元以及实体单元与壳单元的连接。