基于Fluent的纤维过滤器内部流场数值模拟
2019-12-12
(1. 常州纺织服装职业技术学院机电学院,江苏常州 213164; 2.中国矿业大学机电工程学院,江苏徐州 221116)
引言
深层过滤技术广泛应用于石油、化工、造纸、采矿、自来水等行业用水、生产生活用水以及其他工业废水的处理,纤维过滤器以其过滤精度高、日产水量大、对水质适应性强等优点成为深层过滤的典型设备。目前,国内外学者对纤维过滤器的研究主要集中在新型纤维过滤材料的研究以及过滤器结构的优化设计方面,对过滤器过滤效果影响因素的研究较少。采用传统的物理实验方法进行研究时,由于过滤器运行时罐体封闭,无法直观的看到过滤器内部水流特性,增大了深入研究过滤器内部流场分布状况的难度。随着计算机技术的发展和CFD技术的不断成熟,运用流体分析软件对过滤器内部流场进行数值模拟分析成为了可能[1-2]。
1 模型的建立
1.1 多孔介质模型
对于滤纸、多孔滤板和流过充满介质的填充床等的流动问题通常采用多孔介质模型来模拟[3-4]。纤维过滤器纤维滤层比表面积大,流体通过滤层速度小,表现为层流状态,纤维滤料充满滤床,具有多孔介质的属性,因此运用多孔介质模型模拟纤维滤床较合理。
多孔介质模型实际上就是在动量方程中增加包含黏性阻力项和惯性阻力项的源项来表示的,其表达式为:
(1)
式中,Si为i向(x,y,z)动量源项;D为黏性阻力系数矩阵;C为惯性阻力系数矩阵;μ为黏性系数;ρ为流体密度;vj为流场某点沿某方向的速度。
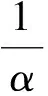
(2)
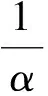
半经验的Ergun公式适用于多种类型的滤床,且适用的Re数范围较宽,可用于计算滤床层的黏性阻力系数和惯性阻力系数。Ergun公式的表达式为:
(3)
式中, Δp为压力降;L为滤层厚度;Dp为颗粒的平均直径;ε为纤维过滤器的孔隙率;v∞为流场某点沿某方向的速度。
纤维过滤器的实际过滤过程表现为层流状态,式(1)中的第二项值很小,忽略后可得Blake-Kozeny方程,其表达式为:
(4)
综合比较式(1)~式(4)可以得出黏性阻力系数和惯性阻力系数表达式分别为:
(5)
(6)
1.2 边界条件设定
对于常见的数值模拟物理模型,Fluent提供了多种常用的边界条件,主要包含速度入口、压力入口出口、内部介质以及壁面等。纤维滤层模型属于不可压缩流动,根据已知条件,选择速度入口(inlet),自由出流(outflow),固定壁面(wall)以及多孔介质阶跃(porous-jump)边界条件。圆柱形滤层物理模型如图1所示[5-6]。
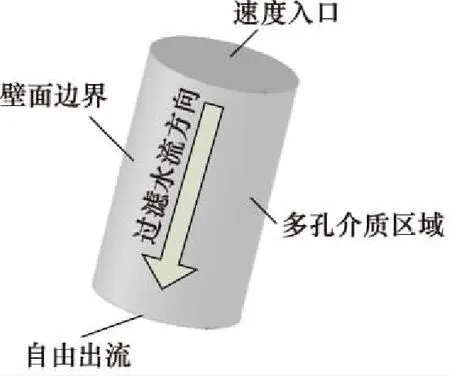
图1 圆柱形滤层物理模型
1.3 黏性阻力系数和惯性阻力系数的计算
多孔介质模型参数的设定是数值模拟的关键,因为该参数的合理设置能够使模拟的滤床更加逼近于真实的纤维滤料滤床,使模拟结果更接近实际值。纤维过滤器滤层所使用的纤维滤料平均直径为50 μm,Dp取50 μm;根据过滤器的实际填充滤料情况,滤床孔隙体积与床层总体积之比为73.5∶100,因此ε取73.5%。将Dp、ε带入式(5)、式(6)可得多孔介质模型的黏性阻力系数和惯性阻力系数为:
(7)
(8)
1.4 网格划分
采用Fluent专用的前处理软件GAMBIT对模型进行网格划分。为了比较不同滤层结构内部压力场和速度场的分布规律,拟对圆柱形滤层、倒锥形滤层和球形滤层三种不同滤层结构进行数值模拟,三种不同结构的滤层厚度相等,且下端出水截面面积相同,三种不同滤层结构模型的网格划分如图2所示。

图2 三种不同滤层结构模型的网格划分
2 数值模拟
2.1 工况分析
对于多孔介质模型滤层,其几何形状参数及滤料本身的多孔介质参数将成为过滤效果的主要影响因素,脉动的入口速度也会对过滤效果以及过滤器内部流场分布产生影响,因此,综合考虑滤层半径、滤层厚度及滤速等因素,对纤维滤层过滤特性展开研究[7-9]。圆柱形滤层的工况如表1所示。
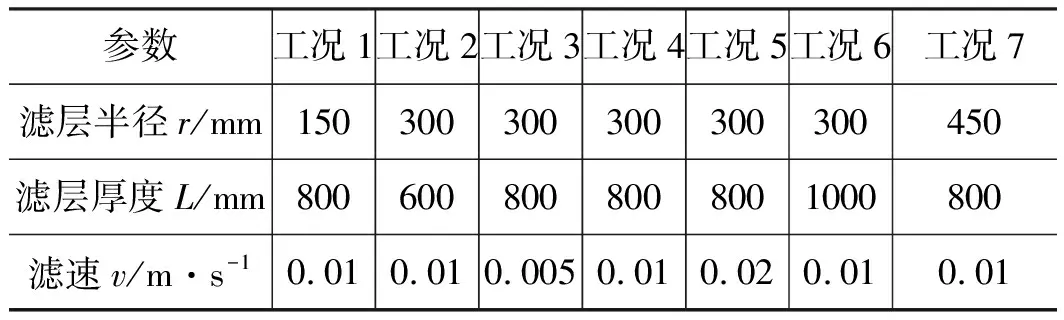
表1 圆柱形滤层的工况
2.2 迭代计算
在Fluent中读取上述Gambit生成的网格文件,对网格进行检查并设定单位后,选取相应的求解器及计算模型,过滤介质指定为水,设定相应的边界条件、误差收敛判据及迭代次数,各种工况下计算结果均能迅速收敛[10-13]。
3 仿真结果分析
3.1 三种不同滤层结构内部压力对比分析
为了比较不同滤层结构内部压力分布规律,即滤层几何形状对滤层内部压力分布的影响规律,对图2所示的三种不同滤层结构内部压力场进行数值模拟计算,y=0 mm截面的压力云图如图3所示。
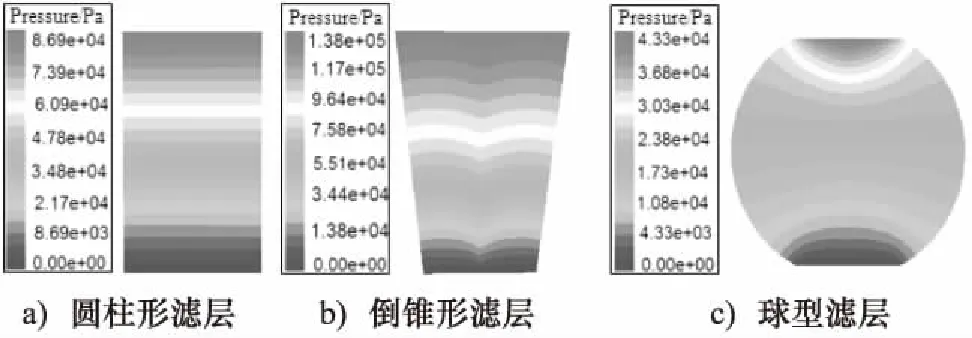
图3 三种不同滤层结构内部压力分布云图
比较图3中可以得出,相同滤层厚度时,圆柱形滤层压力损失与滤层厚度近似呈线性关系;倒锥形滤层进水口较出水口大,下部滤层较密实,也是主要的截污区域,随着过滤的进行,滤层孔隙被不断堵塞,上层滤料截留的污物向下部集中,使压力损失增大;球型滤层进出水口之间有较大的区域没有参与过滤,对水流起到了一定的缓冲作用,能够储存一定的悬浮颗粒,滤床压力损失较小。结果表明,倒锥形滤层压力损失较大,不利于过滤器的平稳运行;球型滤层压力损失较小,但实际参与过滤的滤料较少,不利于出水浊度的提高。
3.2 圆柱形滤层压力场数值模拟结果分析
为了研究滤层厚度、滤层半径以及滤速对滤层压力的影响规律,分别对工况1到工况7进行了数值模拟计算,压力随滤层厚度、滤层半径及滤速的变化规律曲线如图4~图6所示。

图4 压力与滤层厚度的关系(工况2、工况4、工况6)
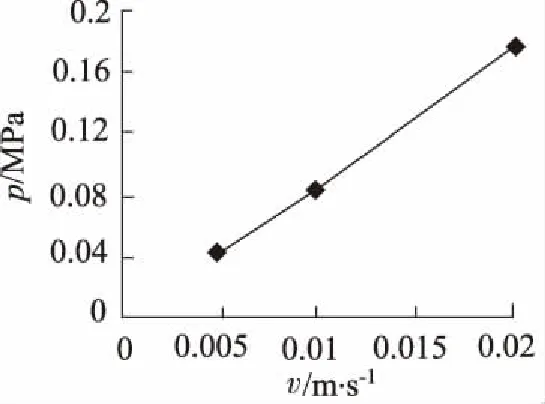
图5 压力与滤速的关系(工况3、工况4、工况5)
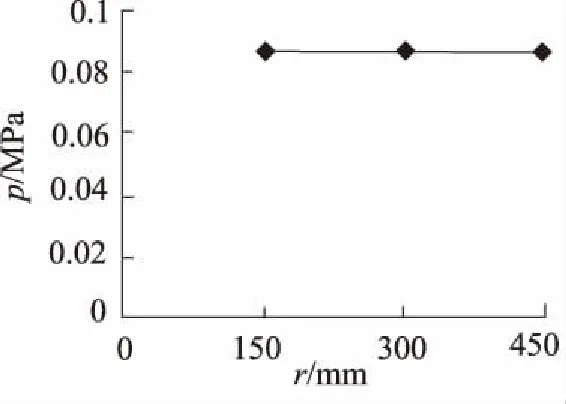
图6 压力与滤层半径的关系(工况1、工况4、工况7)
由图4可知,相同滤层半径和滤速、不同滤层厚度条件下,滤层压力分布规律大致相同:即沿水流方向压力不断减小,压力损失与高度近似呈线性关系,与清洁纤维滤床层压降经验公式相吻合。
由图5可知,相同滤层厚度和半径、不同滤速条件下,最大压力损失与滤速近似呈线性关系。滤床总压力损失随着滤速的增加而增加,这主要是由于随着过滤的进行滤床孔隙不断被原水中的悬浮颗粒堵塞,当达到平衡时增大滤速,悬浮颗粒会继续涌入滤层内,使滤层内部孔隙率减小,增大压力损失。
由图6可知,相同滤层厚度和滤速、不同半径条件下,滤层最大压力损失相同,结果表明,半径对滤层内部压力分布影响较小。
3.3 三种不同滤层结构内部速度分布对比分析
三种不同滤层结构结构情况下,y=0截面的速度分布云图如图7所示[12]。
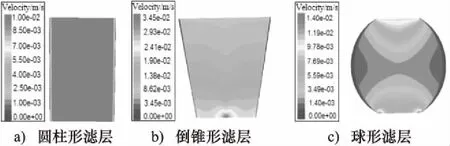
图7 三种滤层y=0截面的速度云图对比
由图7中可以得出,对于圆柱形滤层,滤速除沿壁面位置有所减小外,整个滤层内部的速度变化不大;对于倒锥形滤层,滤速沿整个滤层由上而下逐渐增大,且出水口处速度达到最大为0.0345 m/s,这主要是由于在进出水量相同的情况下,下部截面积减小,因此滤速较大;对于球形滤层,中部截面积较大的区域速度较小,几乎不参与过滤,仅仅起到储存一定悬浮颗粒的作用,出水口处滤速有所增大。结果表明,圆柱形滤层结构内部滤速平稳,有利于过滤器出水水质的提高。
3.4 圆柱形滤层速度场数值模拟结果分析
为了研究滤速对圆柱形滤层内部速度分布的影响规律,分别对工况3、工况4和工况5进行数值模拟计算,y=0截面上的速度矢量如图8所示。
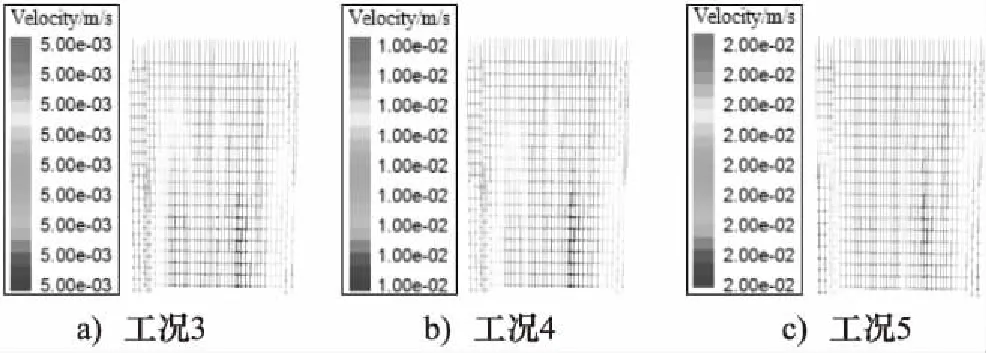
图8 不同滤速时速度分布矢量图
由图8可知,滤层厚度和半径相同条件下,滤速随滤层厚度的变化而变化。上部滤层滤速稳定,中部滤速有所波动,滤层下部速度明显分布不均匀。
为了研究滤层厚度对圆柱形滤层内部速度分布的影响规律,分别对工况2、工况4和工况6进行数值模拟计算,y=0截面上的速度矢量如图9所示。
由图9可以看出,滤层速度和半径相同条件下,滤层厚度增大时,仅仅增大了滤层上部大孔隙区域,由于起主要过滤作用的是滤层中下部,因此满足过滤精度时,滤层厚度的增大对过滤器的过滤精度不会产生影响。
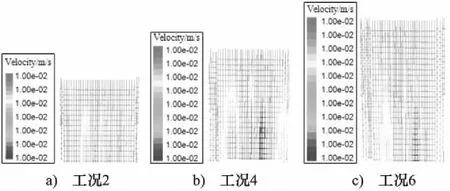
图9 不同滤层厚度时速度矢量图
为了研究滤层半径对圆柱形滤层内部速度分布的影响规律,分别对工况1、工况4和工况7进行数值模拟计算,y=0截面上的速度矢量如图10所示。
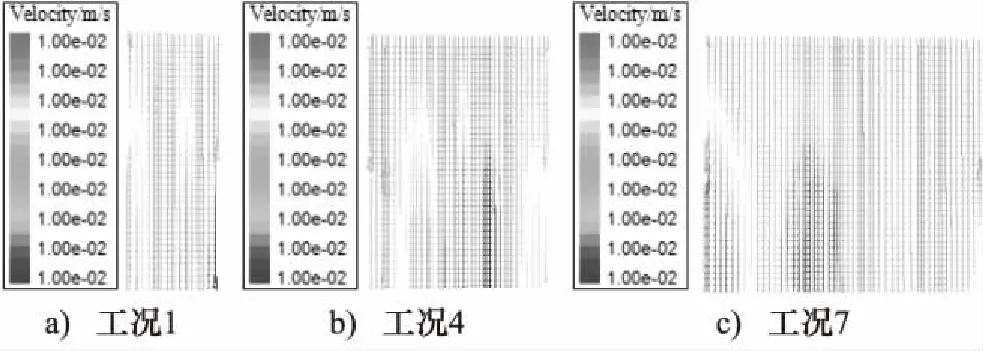
图10 不同滤层半径时速度矢量
由图10可知,滤层速度和厚度相同条件下,滤层半径的变化对滤层内部速度场的分布影响较小,过滤的主要区域集中在滤层中下部。
4 结论
采用多孔介质模型对滤层参数进行设置,运用流体动力学软件Fluent对不同滤层结构的过滤器内部流场进行数值模拟,并主要分析了半径、厚度和滤速对圆柱形滤层结构内部压力场和速度场的影响规律,结论如下:
(1) 不同滤层半径、厚度和滤速条件下,滤层内部压力分布规律大致相同:即沿水流方向压力不断减小,压力损失与高度近似呈线性关系,与清洁纤维滤床层压降经验公式相吻合。由于下部滤料较密实,是滤床的主要截污区域,随着过滤的进行,孔隙不断被堵塞,压力损失增大,因此,下部滤床的压力损失大于上部滤床的压力损失;
(2) 由于上部滤层孔隙率较大,大部分原水能够顺利通过,滤层对速度场分布的影响较小,因此,上部滤层过滤速度稳定;原水流经上部滤层后进入滤层中部,中部滤料较密实,是主要的截污区域,由于滤料分布不均、滤料截留悬浮颗粒后堵塞滤料孔隙等原因导致水流分配的不均,滤速有所波动,从而使下部滤层速度分布不均匀。
