GPS似大地水准面精化及精度分析

2015-12-21范占永蔡东健高笔清

水利与建筑工程学报 2015年6期

范占永，李磊，蔡东健，高笔清

(1.苏州工业园区测绘地理信息有限公司，江苏苏州215001;2.张家港市城市测量队，江苏张家港215600;3.江西理工大学建筑与测绘工程学院，江西赣州341000)

随着现代空间测量技术的迅速发展，大地水准面理论研究也不断深入，区域似大地水准面精化精度已发展到厘米级的研究阶段［1－3］。

大地水准面精化的方法一般有GPS水准拟合法、重力法及组合法三种方法［4－7］。当不考虑地球重力场模型和重力等数据影响的时候，在某小区域范围里，利用高精度的GPS大地高和精密几何水准数据通过最小二乘方法来拟合区域似大地水准面能得到良好的效果［8］。

通过一定方法对原有的似大地水准面进行精化，达到在区域范围内代替低等级水准测量和三角高程测量的目的，从而使精化后的似大地水准面可以通过GPS(RTK)测量就能方便快速获取该区域内任一点的正常高。

1 区域似大地水准面精化

空间大地测量中，有大地高系统、正高系统、正常高系统，它们分别是以椭球面为基准、大地水准面为基准、似大地水准面为基准。大地测量中，将似大地水准面与椭球面之间的高差称之为高程异常［9－10］。

GPS水准点就是GPS得出大地高和通过水准测量得出正常高的点。由GPS点获得大地高H大，水准点获得正常高H正，两者(大地高和正常高)作差可得高程异常NGPS=H大－H正;由于通过原似大地水准面格网值内插法也可得出该点的高程异常，从而有差值，利用此差值即可构建似大地水准面拟合模型。在似大地水准面拟合模型中，平面模型、曲面模型、切比雪夫模型、三次多项式模型以及多面函数模型等一般被学者们常用来构建精化似大地水准面拟合模型［11－15］。

曲面拟合法的原理是将GPS水准点获得的高程异常近似看作各点坐标的曲面函数，通过此拟合函数从而来计算其他地方的GPS点的高程异常，从而得到正常高，它也是区域似大地水准面精化常用的一种方法。由于本文所精化的区域北宽南窄，呈三角形，地势西南向东北略有倾斜，属平原地带，总面积约1 000 km2，境内最高海拔136.6 m，故拟采用二次多项式曲面拟合法来拟合高程异常从而进行该区域的似大地水准面的精化，二次多项式的数学模型如下:

其中，a0，a1，a2，a3，a4，a5为拟合系数;φm，λm为拟合区的中心纬度和经度。设B=［1，φ -φm，λ -λm，(φ- φm)2，(φ - φm)(λ - λm)，(λ - λm)2］T=［a0，a1，a2，a3，a4，a5］为拟合系数。当有足够的观测值ΔN'(大于或等于6个)后，对于函数模型V=BÂΔN'，利用经典最小二乘平差方法，可以得到拟合系数的估值。拟合系数求出以后，根据GPS测点的经纬度代入此模型中就可以求得其高程异常，进而可得到测点正常高。

根据上述大地水准面精化原理，开发具有可操作界面的应用程序，程序在.NET3.5框架下，采用C#语言进行开发。利用该程序实现此精化范围内大地高向国家85高程基准的转换。

2 实例及精度分析

某区域实测GPS水准点36个，其中，GPS点为C级GPS控制网点，水准点通过二等水准测量得到，GPS水准点(通过经纬度体现)分布位置如图1所示，利用实测得到的36个二等水准点与原有似大地水准面内插法得到的正常高相比较并作精度统计，统计结果如表1所示。

图1 GPS水准点分布位置

表1 原似大地水准面精度统计

根据图1中GPS水准点分布情况，该区域进行似大地水准面精化采用二次多项式拟合法结合最小二乘平差方法，考虑到需作内、外符合精度比较，数据处理时只选取18个特征点参与拟合计算出似大地水准面模型，剩下的18个点作为外符合精度检核点。利用精化后的似大地水准面计算出36个点的正常高，然后同精化前的水准测量的正常高相比较，并按式(2)、式(3)、式(4)分别依此计算出似大地水准面精化后正常高的平均偏差、最大偏差和中误差:

本文通过似大地水准面精化成果将参与精化似大地水准面计算的18个GPS点的大地高转换为正常高，与水准测量所得的正常高相比较，得到似大地水准面精化成果的内符合精度，数据如表2所示。

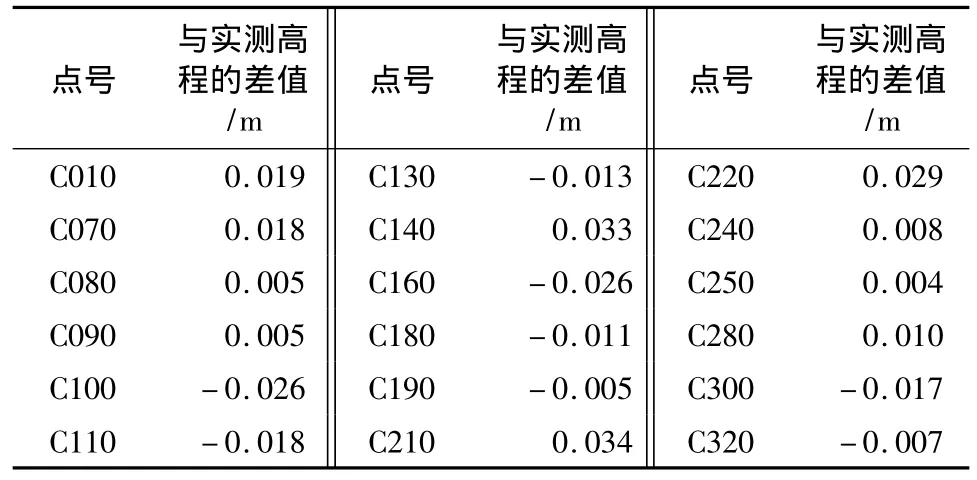
表2 精化似大地水准面内符合精度统计

通过式(2)、式(3)、式(4)，可得精化后内符合平均偏差为0.016 m，最大偏差为0.034 m，中误差为 ±0.019 m。

将剩下没参与拟合的18个GPS点的大地高导入似大地水准面精化成果中计算拟合模型中的正常高，所得到的正常高与已知的水准高进行比较，从而得到似大地水准面精化后的外符合精度。外符合数据如表3所示。

同理，通过式(2)、式(3)、式(4)，可得精化后外符合平均偏差为0.013 m，最大偏差为0.041 m，中误差为 ±0.018 m。

表3 精化似大地水准面外符合精度统计

由表1中数据可得出，原似大地水准面平均偏差为 0.016 m，最大偏差为 0.052 m，中误差为±0.020 m。由此可得知，精化后的似大地水准面成果相较于原似大地水准面精度由±0.020 m提高到±0.018 m，这一结果验证了似大地水准面精化的正确性和有效性。

为了充分利用GPS水准点数据，将36个点的GPS大地高成果直接用原有似大地水准面转换为正常高，与实测水准高比较，发现没有超过三倍中误差的点，故利用所有点，即36个GPS水准点全部作为拟合点来参与拟合计算第二次区域似大地水准面精化模型。第二次精化后，内符合精度统计结果如表4所示。

表4 第二次精化似大地水准面内符合精度统计

从表4可得出内符合精度情况，平均偏差为0.013 m，最大偏差为 0.041 m，中误差为 ±0.016 m。与第一次内符合精度比较，平均偏差和中误差均优于第一次，虽然C140 GPS水准点相较于第一次偏差有所增大，但最大偏差依然没有超过第一次的最大偏差，整体精度依然比第一次精化后的结果有提高。

图2所示为:原似大地水准面、第一次精化似大地水准面、第二次精化似大地水准面的计算的正常高与实测水准高程的较差，可得出虽然精化之后的结果大体上优化了精度，但是仍然有少数点的高程偏差反而会增大，这可能是由于GPS水准点本身误差就存在相对较大的情况，也可能是由于这些点处于似大地水准面精化边界所造成的。

图2 似大地水准面拟合高程与实测水准高程较差

根据本区域精化后的似大地水准面内外符合精度可知，高程异常精度满足一般工程要求(城市似大地水准面精度要求为±0.020 m)。由以上数据可得，原似大地水准面外符合精度为0.02 m(与实测水准点相比较);第一次精化时选取18个点作为拟合点，18个点作为外符合精度检核点，得第一次精化后内符合精度为 ±0.019 m，外符合精度为±0.018 m;第二次精化利用GPS水准点所有点作为拟合点，得第二次似大地水准面内符合精度为±0.016 m，故本区域选用第二次精化成果为最终精化成果用于工程实践中。