既有预应力结构现存预应力数学模型研究

高 杰，黄 颖

(福建船政交通职业学院，福建福州350007)

如何在经济与技术许可的情况下准确地评估预应力混凝土桥梁承载力已成为各个国家和地区桥梁可靠性研究的热门课题［1－3］。对大量既有预应力混凝土桥梁而言，有效预应力是决定其承载能力的重要因素，通过对此类桥梁进行检测和评估，了解现存预应力情况，可使在役预应力混凝土桥梁的技术改造决策更加科学、改造技术方案设计更加合理、经济，具有重要的社会意义、经济价值和广泛的应用前景。

目前，在大量的既有预应力混凝土桥梁检测中，对桥梁现存预应力的估计都存在很大的盲目性和主观性，如果没有在桥梁建设初期安装健康监测系统，运营期现存有效预应力值就很难准确估计。预应力混凝土桥梁常用的评估方法中:基于规范的评估方法［4］主观性强，评估结果误差较大;荷载试验法［5］精度高，但是需要花费大量的人力物力财力，并且存在一定的风险性;基于裂缝统计特性法［6］需要建立在大量的检测数据基础上;结构动力特性评估方法［7］的准确程度从目前的研究结果看，说法不一，准确性还有待评估。

在既有桥梁服役过程中，桥梁的现存预应力直接影响到桥梁的承载能力，而直观反映出来的就是桥梁的挠度和基本频率，通过建立桥梁相对容易检测值——包括桥梁挠度、桥梁基本频率与现存预应力之间的函数关系［8－10］，通过检测得到桥梁响应代入到此函数关系中，相对准确的获得桥梁的现存预应力，便于工程的实际应用。目前国内外对桥梁基本频率和有效预应力之间的函数关系做了许多研究，也取得了一些有益的成果［11－12］，本文主要研究桥梁挠度与现存预应力之间的关系，利用既有构件静力承载力试验结果和有限元分析结果，采用数学优化分析综合分析软件1stOpt 6.0程序对构件各代表性截面的有限元分析结果进行拟合，建立基于荷载作用下桥梁挠度改变量的现存预应力预测模型，为实际工程提供一定的参考依据。

1 预应力简支梁三维有限元模型建立

利用福建省福州市鳌峰闽江大桥(闽江三桥)需要拆除重建的机会，从原桥中选取一跨进行切割，将切割梁单元运至试验室进行既有结构现存预应力的试验研究，具体试验梁的几何及材料参数见文献［13］，采用有限元软件ANSYS建立该切割板梁单元的三维有限元模型。其中Solid65单元模拟混凝土，普通钢筋和预应力钢筋均采用Link8，粘结滑移单元Combin39模拟预应力钢筋单元和混凝土单元之间的粘结滑移关系［14］，混凝土的本构模型为Darwin等［15］提出的增量式正交各向异性单轴等效应力—应变本构模型，混凝土开裂模型采用分布式裂缝，假定混凝土开裂后单元依旧连续，破坏准则采用三轴受力下的Drucker－Prager强度准则;钢筋的材料模型采用双折线理想等效强化模型弹塑性应力—应变关系，钢筋屈服后考虑应变强化。依此建立了该切割预应力板梁单元的三维有限元模型见图1，模型由22540个混凝土单元，501个预应力筋单元和3840个钢筋单元组成。

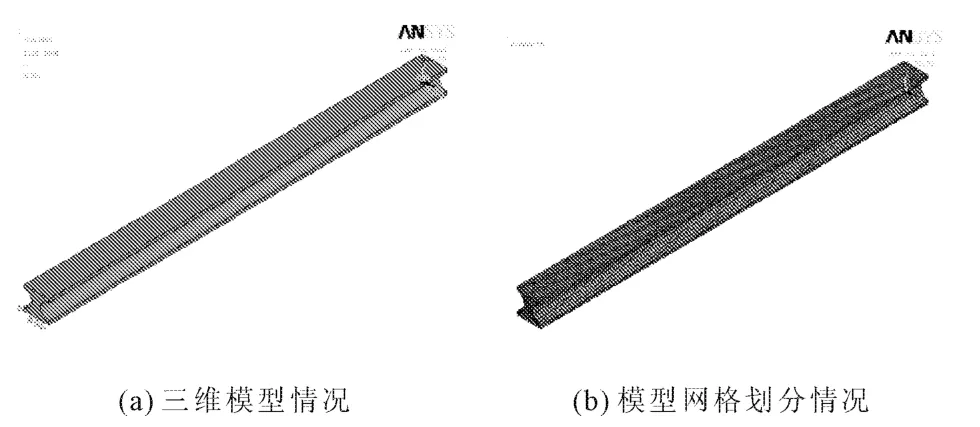
图1 有限元模型三维视图

2 预应力变化情况下加载规律分析

为了研究在预应力损失情况下，外荷载变化对结构响应的影响，同时在梁体三等分处作用对称集中荷载，跨中截面属于“纯弯段”，此种加载方式能尽量具有代表性的三个截面:1/4、跨中、3/4，单元构件减少剪力效应对结构响应的影响。分析截面选取简支梁面位置示意图见图2，对其进行外荷载作用下随着预应力变化的结构响应分析，在有限元约束建模中，支座两端竖向约束和横向约束同时施加，这样可以避免梁体的扭转，以免计算结果的不收敛。分析时预应力最大值选取设计张拉控制力565 kN，通过模型的静力加载分析得到在预应力变化情况下不同外荷载作用简支梁1/4、跨中(1/2)、3/4三个截面的挠度，有限元分析结果见图3。

图2 单跨预应力混凝土空心板单元构件示意图

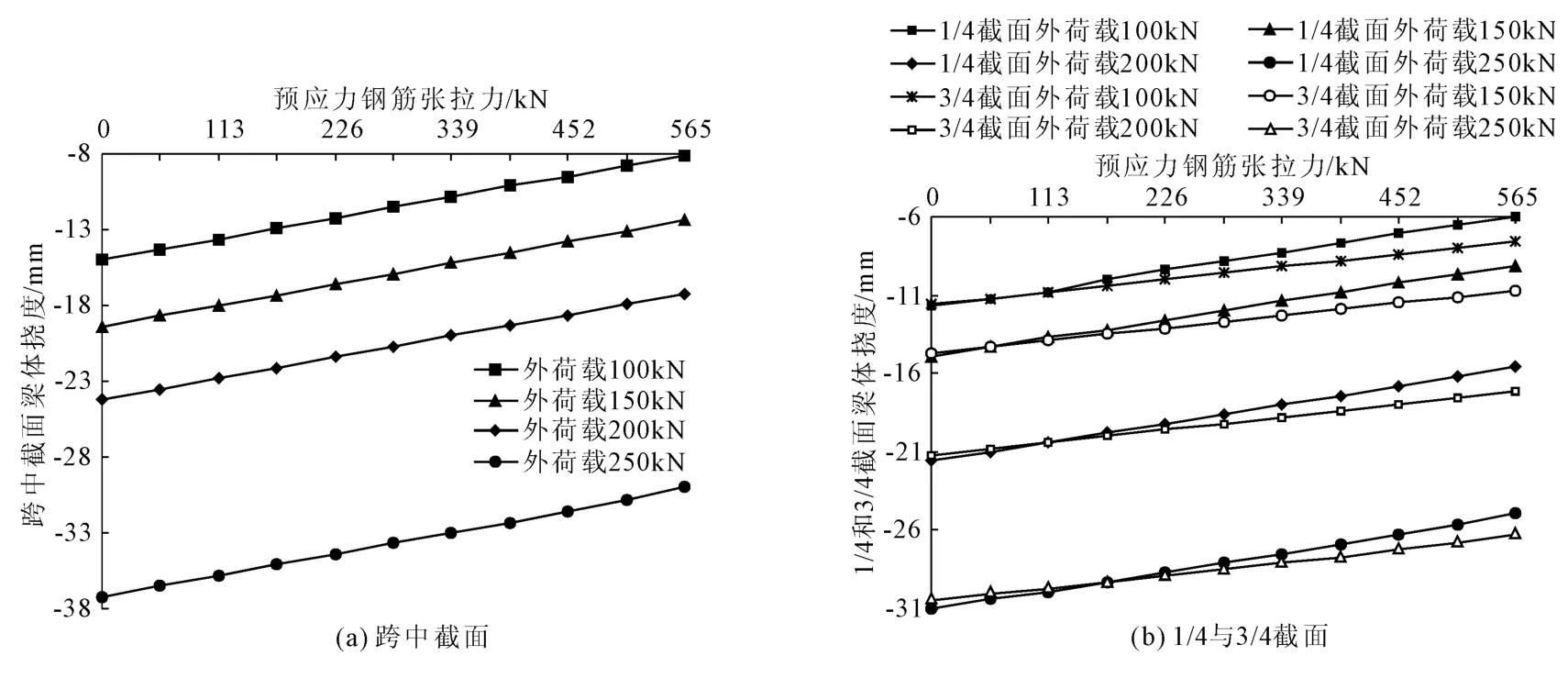
图3 各截面外荷载—挠度示意图

从图3(a)的分析可以看出跨中截面挠度在各级加载作用下，预应力和响应之间呈现明显的线性关系，在相同加载情况下，预应力越大，梁体挠度越小;加载量越大，梁体响应也越大。从图3(b)可知，1/4截面和3/4截面梁体挠度不同，在各级加载作用下，3/4截面挠度明显大于1/4截面，从梁截面示意图2可以看出，该既有梁单元的预应力钢筋线形布置以跨中为中心轴，左右为不对称布置，也就造成原本对称的两个截面响应不同。3/4截面处为直线布筋，而1/4截面处为曲线布筋，在预加力作用下，曲线布筋梁可以看成承受向上的均匀荷载以及轴向力，向上的均匀荷载可以用来抵消外加力产生向下的荷载，而直线布筋就只有轴向力，因此曲线布筋形式使得预应力效应更强，这也就是在相同荷载作用下，3/4截面挠度比1/4截面大的原因。

3 现存预应力和挠度关系预测模型建立

在对既有结构的检测中，结构的初始响应难以获得，因此分析中，选取一个加载状态作为分析的初始状态，通过求差计算，获得每一次加载级别结构响应与初始状态之间的差值，利用数值分析软件1stOpt 6.0建立简支梁关键截面挠度变化相对值与预应力损失关系的数学模型。在本文的分析中，以外荷载100 kN作为分析的初始状态，将每一级别外荷载作用下，预应力改变获得的挠度值减去外荷载为100 kN时的挠度值，得到挠度改变量Δδ，Δδ的计算值见表1，通过分析和试算，将预应力损失与初始预应力之间的比值定义为λ，即:

式中:Ns为预应力损失量，kN;Ncon为张拉控制力，kN。

外荷载P和预应力单位均取kN，挠度增量Δδ单位取mm，以预应力损失度λ在0% ～100%为分析对象，将表1中的数据Δδ作为因变量，λ映射到X轴作为自变量，将两者进行非线性拟合，通过一系列数学模型的试算，得到最终的构造函数为:

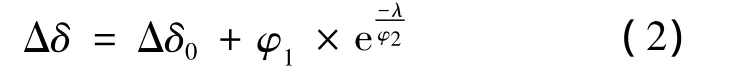
其中:Δδ挠度增量，mm;Δδ0为构件未施加预应力在外荷载增量作用下挠度值，mm，与外荷载施加方式有关，本文分析取沿着梁跨方向对称加载，因此:

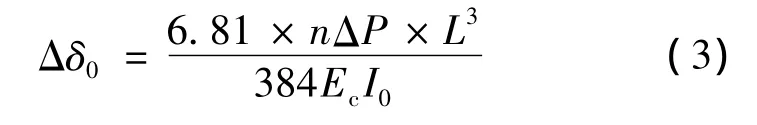
式中:φ1为挠度常数，与支承条件、梁体截面形式、普通钢筋配筋率等因素有关;φ2为预应力影响系数，与预应力钢筋布筋形式、预应力钢筋偏心距等因素有关;n为外荷载加载级别;ΔP为外荷载分级加载量，kN;EcI0为无预应力梁体毛截面刚度。

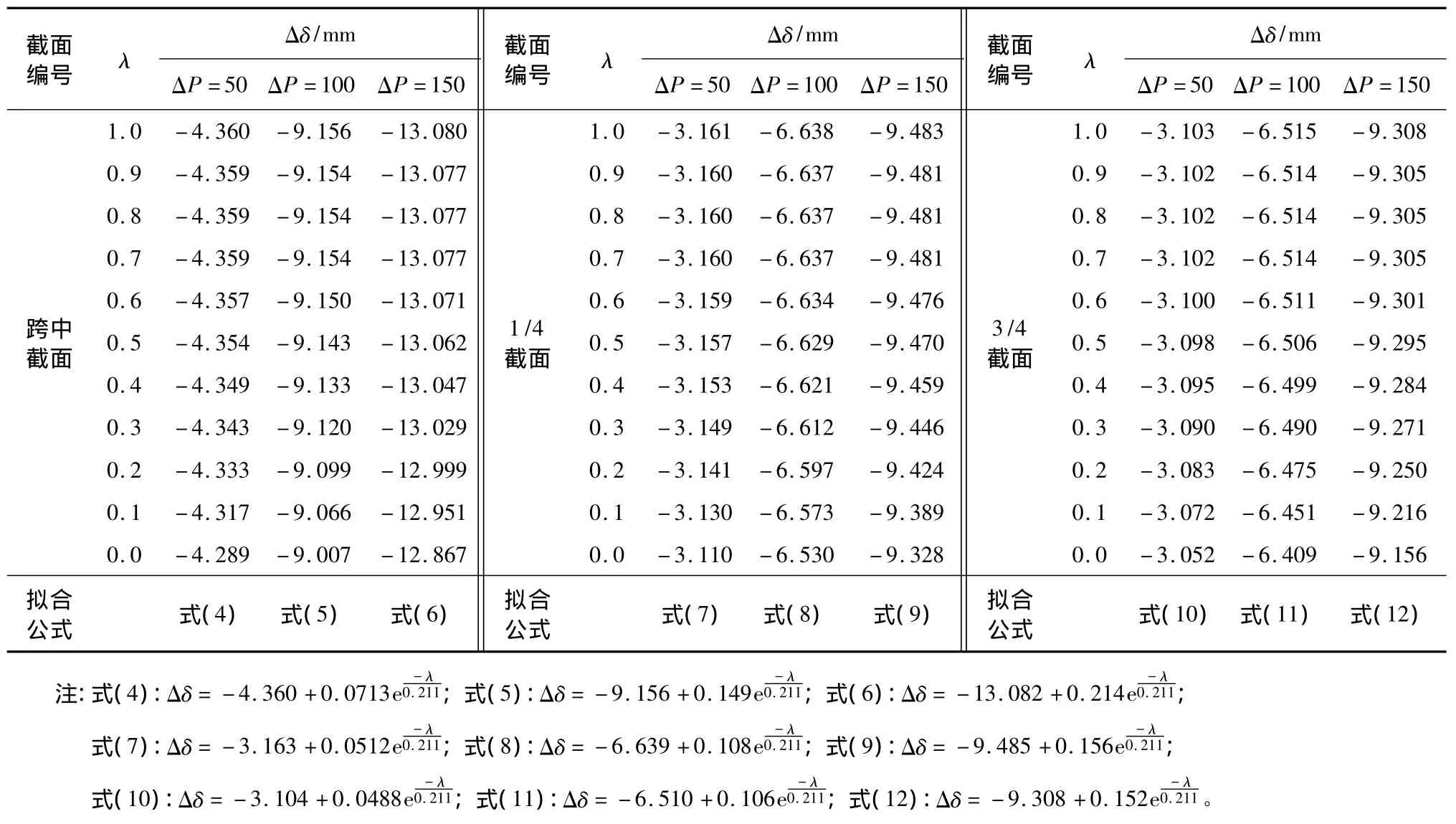
表1 截面挠度增量—预应力损失度数学模型

得到的数学模型及相关参数见表1，对建立的数学模型对数据进行拟合分析，从图4各截面(a)拟合曲线可以看出，建立的三个截面挠度增量数学模型拟合相关系数达到0.99以上，确定系数也达到0.98，证明公式是有效的，从图4各截面(b)可以看出，误差分布很离散，没有明显的规律性，进一步说明拟合效果很好。依照此公式，在对既有结构或者构件进行预应力损失估计时，只需要通过静力分级加载试验，首先将一级加载获得结构响应作为初始状态，再通过下一级加载获得结构的挠度减去初始状态挠度，获得挠度增量，代入所建立的数学模型就可以获得预应力损失度，进而计算出结构现存预应力，完成结构现存预应力的预测。

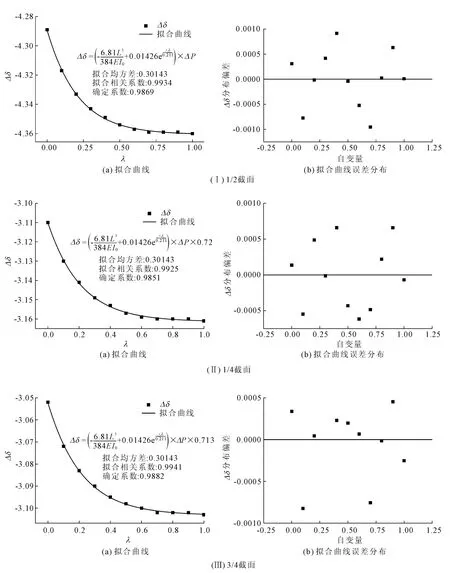
图4 各截面挠度增量与预应力损失度拟合曲线

4 试验对比分析

通过在分级加载下的挠度变化量Δδ=δPi－δP0和预应力损失度λ=Ns/Ncon之间的数学模型，在对既有结构预应力损失的评估中，只需要通过静力加载获得分级荷载作用下的挠度变化量，通过该数学模型公式就可以计算出预应力损失度，进而估计结构或者构件的现存预应力。对试验室试验梁在分级加载下的挠度响应结果进行分析，将外荷载等于100 kN的工况减去初始状态工况试验结果，获得挠度变化量见表2，将挠度变化量代入拟合公式，就可以推算出每个截面的预应力损失度λ，分析得到三处截面预应力损失度分别为14.6%、22.7%、18.8%，对应的该既有结构现存预应力值约为437 kN，与通过应力释放法试验［9］获得的预应力损失度进行对比，1/4截面的误差较大为8.2%，跨中截面和3/4截面误差还是比较满意的，证明了数学模型的有效性。

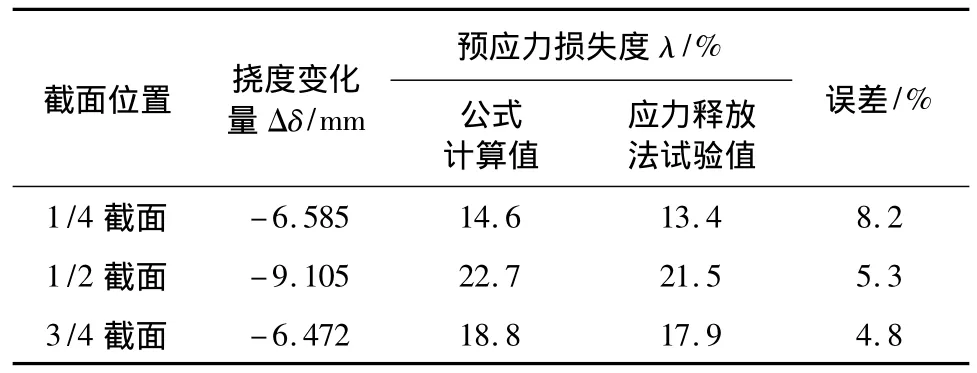
表2 试验梁预应力损失度估算

5 结语

本文利用有限元软件ANSYS建立既有预应力混凝土板梁单元三维有限元模型，分析了在预应力递增情况下外加荷载变化的结构挠度响应，获得截面的荷载—挠度变化曲线。利用1stOpt软件中的优化算法:麦夸特法和通用的全局优化法，建立了简支梁1/4截面、1/2截面、3/4截面在外荷载分级作用下挠度变化相对值与预应力损失度关系的数学模型，通过该数学模型可以推算既有结构的预应力损失值。将推算结果与应力释放法试验获得的预应力损失度进行对比，误差基本在5%以内，证明了数学模型的有效性和可应用性。

［1］宗周红，任伟新，郑振飞.既有桥梁承载能力评估方法［J］.地震工程与工程振动，2005，25(5):147-152.

［2］张劲泉.我国公路桥梁承载能力检测评定技术的现状与发展［J］.公路交通科技，2006，23(4):15-17.

［3］赵 煜，贺拴海.在役预应力混凝土箱梁开裂后承载力评估［J］.同济大学学报:自然科学版，2010，38(9):12-15.

［4］中华人民共和国交通部.公路钢筋混凝土及预应力混凝土桥涵设计规范:JTG D62－2004［S］.北京:人民交通出版社，2004.

［5］洪 涛，卢玫 ，周储伟.预应力梁结构响应的简要荷载试验法研究［J］.新技术新工艺，2013(4):22-26.

［6］赵 煜，贺拴海.在役预应力混凝土箱梁开裂后承载力评估［J］.同济大学学报:自然科学版，2010，38(9):12-15.

［7］Kim J T，Ryu Y S，Chung Bang Yun.Vibration-based method to detect Prestress-loss in beam－type bridges［R］.Proeeedings of the SPIE－The International Society for Optical.

［8］黄 颖，许永吉.基于ANSYS的预应力混凝土空心板梁单元挠度与固有频率的研究［J］.南昌大学学报:工学版，2014，36(1):27-30.

［9］卢志芳.考虑时变性和不确定性的混凝土桥梁收缩徐变及预应力损失计算方法［D］.武汉:武汉理工大学，2011.

［10］黄 颖，房贞政.在役预应力混凝土简支梁永存预应力的数值模拟研究［J］.福州大学学报:自然科学版，2013，41(6):1110-1114.

［11］Breccolotti M，Ubertini F，Venanzi I.Natural Frequencies of Prestressed Concrete Beams［C］//Theoretical Prediction and Numerical Validation，Proceeding of the XIX Aimeta Conference，Ancona，Italy，2009:14-17.

［12］张耀庭，汪霞利，李瑞鸽.全预应力梁振动频率的理论分析与试验研究［J］.工程力学，2007(8):116-120.

［13］黄 颖，房贞政.已服役20年预应力结构现存预应力的试验研究［J］.哈尔滨工程大学学报，2014，35(10):1201-1205.

［14］王新敏.ANSYS工程结构数值分析［M］.北京:人民交通出版社，2013.

［15］Darwin D，Pecknold D A.Analysis of RC shear panels under cyclic loading［J］.Journal of the Structural Division，ASCE，1976，102(2):355-369.