考虑流固耦合的降雨入渗过程对非饱和土边坡的影响研究

荆周宝，刘保健，解新妍，李 哲

(1.长安大学公路学院，陕西西安710064;2.长安大学特殊地区公路工程教育部重点实验室，陕西西安710064)

降雨是一种常见的天气现象，山区边坡受降雨影响产生崩塌滑坡等地质灾害屡有发生，边坡多为非饱和土质，这说明雨水对其力学变形行为有很大的影响。雨水入渗会在边坡内形成渗流场，在渗流场的影响下，非饱和土质边坡这一固体会产生力学变形行为，边坡固体的变形又将会对雨水渗流场产生影响，二者相互作用最终导致非饱和土质边坡的变形，甚至崩塌，这就是一种典型的非饱和流固耦合现象。近些年，流固耦合已经吸引了国内外许多专家学者为之探究，并取得了一定的成果。Papagiannakis等［1］用Galerkin加权余量原理推导了二维稳态渗流的有限元形式;在非饱和问题中，Lumbp［2］运用了伽辽金有限元方法来求解;孙冬梅、荣冠等［3－4］都对饱和—非饱和渗流问题进行了研究，并获得相应成果。但目前大多数研究还是以某一单一场为主，并没有考虑渗流场与固体变形之间相互影响这一耦合作用。

为此，本文在前人研究的基础上，利用大型通用有限元软件ABAQUS强大的非线性分析能力，以一典型理想边坡为算例，进行了考虑流固耦合和土水特征曲线的降雨入渗对非饱和土坡影响的有限元数值模拟研究，得出了降雨对非饱和土质边坡的影响特征，提出了在实际工程设计防护中考虑耦合作用和雨水入渗影响的合理性和必要性，为进一步研究非饱和土质边坡稳定性预测、边坡防护及相关工程设计打下了基础。

1 非饱和土边坡降雨入渗过程分析

1.1 降雨入渗理论

入渗率qr［5］是指诸如土体类的多孔介质发生入渗过程时，单位面积在单位时间内所通过的水量。它是雨水渗入土质边坡过程的重要参数，常以cm/s或m/d为单位。入渗率反映土体的入渗能力。

Horton［6］在水文学中提出，雨水落至地表，不断浸入土体，随着时间的增加，土体入渗率逐渐减小，最终趋于稳定，即对于诸如土壤类多孔介质，都有一个随时间变化并最终趋于稳定的可渗入最大流量值，这一最大流量值所在趋势线被称为极限曲线，这个曲线代表了多孔介质的入渗能力。入渗能力在降雨过程中先随时间的增长而降低，最终趋于稳定，达到极限流量而不再变化。降雨之初入渗能力的动态变化主要是由雨水充填土体孔隙的不断变化而造成的，最终土体饱和，入渗能力也就趋于一个不变值。在降雨过程中任一时间段，如果降雨强度超过了入渗能力，那么超过的雨水将无法深入土体，而是从地表流走。如图1所示。

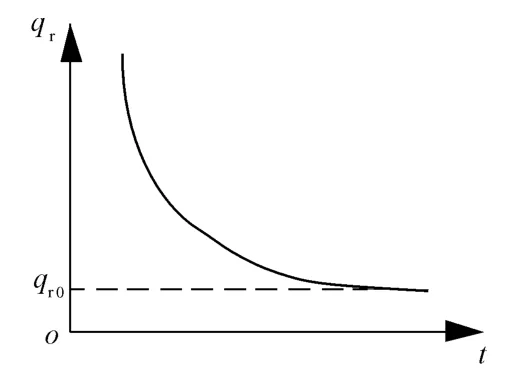
图1 入渗能力示意图

土体的入渗能力是以入渗率这一参数体现的。根据饱和—非饱和渗流理论［7］，qr(t)为任意时刻t对应的入渗率，q(0，t)为相同时刻地表土壤水分运动通量，两者的值相等，即有:

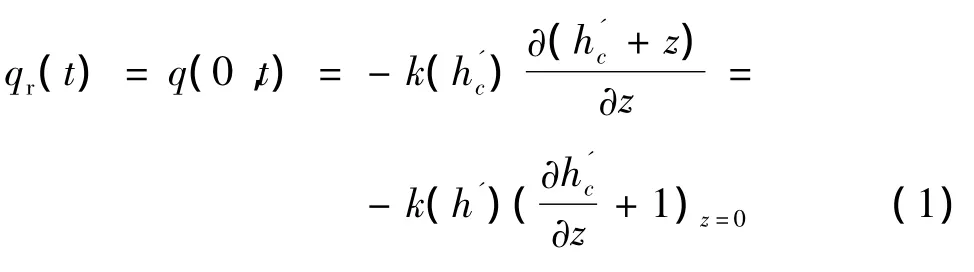
式中，z坐标取向上为正，hc在一般土中为压力水头，在非饱和土称为基质势。

非饱和土质边坡降雨入渗过程中，开始时边坡土体干燥，雨水落至地表形成积水，由于含水率梯度的绝对值在地表处较高，压力水头梯度也相应较大，所以雨水入渗过程之初入渗率qr(t)值很高。随着雨水不断浸入，压力水头梯度的绝对值逐渐降低，入渗率值也相应减小;当入渗末期即土体趋于饱和时，入渗率值趋于稳定，呈现不变的趋势，这与Horton所提出的多孔介质土体入渗能力随时间变化关系理论的特征相一致。

1.2 降雨入渗的过程

降雨入渗是雨水渗入土体的物理现象，在天然条件下，降雨入渗是一个涉及多个物理力学参数变化的复杂过程，为了描述这一复杂过程，1973年，Mein等［8］提出了降雨入渗过程中的降雨强度q、土壤允许入渗的容量fp、土壤饱和时的水力传导系数Kws三大因子，用来描述降雨入渗的复杂过程［9］:

(1)q＜Kws:降雨之初，边坡土体视为干燥状态，雨水落至地表将全部入渗，而不会出现地表径流，此时水的入渗率基本呈不变状态。

(2)fp＞q＞Kws:土壤允许入渗容量fp与入渗深度成反比，即入渗深度越深，土壤允许入渗容量越小，但此时降雨强度小于土壤允许入渗容量，全部雨水渗入土体，入渗率值不会变小，且呈现较高值，这种状态下坡面即为流量边界。

(3)q＞fp:随着降雨入渗过程的不断进行，雨水不断渗入边坡土体，土壤允许入渗容量fp逐渐降低，使得部分降雨并未渗入边坡土体，而是形成径流，从地表流走，这说明边坡土体此时已处于饱和状态。入渗率值也在降雨强度达到并超过土壤允许入渗容量后，逐渐减小。

2 流固耦合基本原理及在有限元中的求解

2.1 基本原理

流固耦合是指应力场和渗流场的相互作用，这种相互作用在力学领域中被称之为流—固耦合作用，在地质岩土领域常称之为水—岩(土)相互作用。简言之，流固耦合就是两种或两种以上的物质相互作用的一种动态过程。在岩体中，渗流场向裂隙壁施加法向渗透压力和切向拉力，从而影响了岩体应力分布;应力场会对裂隙宽度产生影响，裂隙的渗透系数又与裂隙宽度相关，即裂隙的渗透系数会随裂隙宽度的改变而改变，故应力场影响着岩体的渗流场。同理，在土体中，渗流场向土体作用面施加的渗透压力和渗流体积力会对土体的应力分布产生影响;而应力场的改变会对土体的体积应变和土体孔隙率产生影响，进而改变土体渗透系数，即应力场影响着土体的渗流场。所以说在岩(土)体中，应力场和渗流场是相互作用、相互影响的，在研究相关领域问题时这种相互关系的考虑是必不可少的。因此，为了更真实的分析降雨入渗过程对土质边坡的影响，必须考虑渗流和应力的耦合。

2.2 耦合场计算方法

流固耦合的计算方法目前大致分为两种:间接耦合和直接耦合［10］。间接耦合是首先通过渗流计算得到应力计算所需要的孔隙水压力，然后将该孔隙水压力调入到应力分析中，即渗流场和应力场是分别计算再相互调配耦合的，而直接耦合是通过对应力场和渗流场进行空间离散来建立数学模型，进而求得其解析解来达到完全耦合。

ABAQUS软件是采用直接耦合的方法来分析研究应力场和渗流场的耦合作用的，分析计算过程中程序对应力场节点位移和渗流场的孔隙水压力进行空间离散，将时间积分引入渗流方程中，再将应力、渗流方程转化为矩阵形式，并对其进行牛顿迭代从而得到耦合作用的控制方程，同时对模型建立初始边界条件和应力渗流条件，然后在设置时间步内进行解析解，并使耦合方程及其求解过程满足模型设置条件，最终实现真正意义上的流固耦合。基于此，本文采用ABAQUS软件进行直接耦合分析计算。

2.3 耦合的有限元求解控制方程

诸如土体类多孔介质的孔隙结构比较复杂，耦合的有限元求解视“流”(体)和“固”(体)为连续体相互重叠，采用连续介质法，将多孔介质系统用连续系统来代替，这样就能够用连续系统内的可测定变量来描述多孔介质系统内的应力渗流过程，从而使得流固耦合控制方程建立在具体可测的物理力学变量基础之上，来更好的实现流固耦合。ABAQUS正是基于这种方法来进行流固耦合分析计算的［11］。

虚功原理可以用来表示固体材料的应力平衡，在t时刻，一定体积固体材料内构成的虚功原理为:

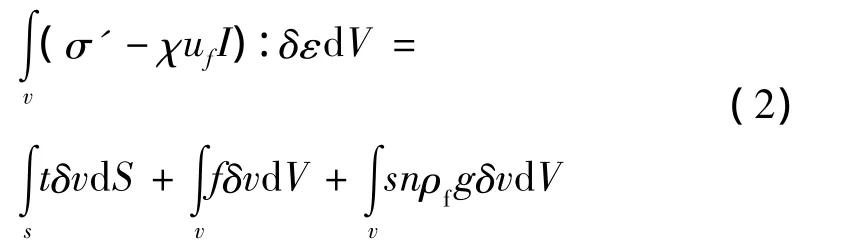
式中:δε =sym(∂δv/∂x)表示虚变形速率，σ'为有效应力，δv为虚速度场，t为单位面积的表面力，f为单位体积的体积力，s为固体材料饱和度，n为固相材料的孔隙率，ρf为流体密度，g为重力加速度。

耦合的有限元求解过程中采用位移有限元的方法，将虚功方程用拉格朗日公式离散化，从而得到固体和流体材料的有限元网格，因此，流体需要满足耦合连续控制方程，使其在相同时间增量内流入的流量等于其体积增加的速率，即

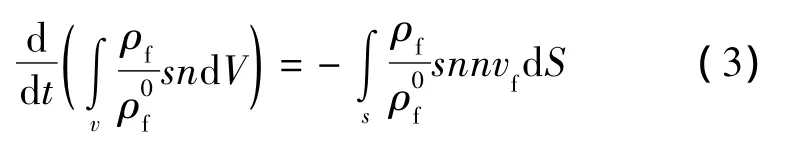
式中:vf表示渗流速度，n为面S的外法线方向，ρ0f为参照密度。

3 基于ABAQUS的有限元数值模拟的实现

3.1 屈服准则的选取

有限元法中包含的本构模型较多，岩土体一般多采用理想弹塑性本构模型:如Drucker－Prager(简称D－P)模型和Mohr－Coulomb(简称M－C)模型等［12］。其中较之D－P模型M－C是最经典的土力学模型，比较实用，该模型对于一般的岩土非线性分析来说结果是充分可靠的，因此被广泛用于模拟大部分岩土材料。但该模型在屈服面上存在棱边或者尖角，这可能会使运用该模型本构进行分析计算的模型收敛缓慢甚至收敛困难。而ABAQUS软件则采用了扩展的Mohr－Coulomb准则，消除了经典的M－C模型在屈服面处的棱角，使其变得连续且光滑，有利于模型分析计算的收敛性。因此，本文最终选取扩展的Mohr－Coulomb理想弹塑性本构来对边坡土体进行模拟。

即屈服准则为:

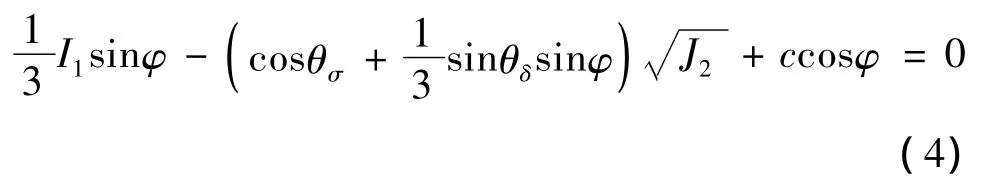
式中:I1为应力张量第一不变量，J2为应力偏张量的第二不变量;θσ为应力罗德角;φ为土的内摩擦角;c为土的黏聚力。

3.2 流动法则的选取

有限元流动法则分为关联流动法则和非关联流动法则，ψ(剪胀角)的取值决定了关联流动法则的类型:当ψ=φ时，为关联流动法则;当ψ≠φ时，为非关联流动法则。Mohr－Coulomb的塑性势方程为［13］:

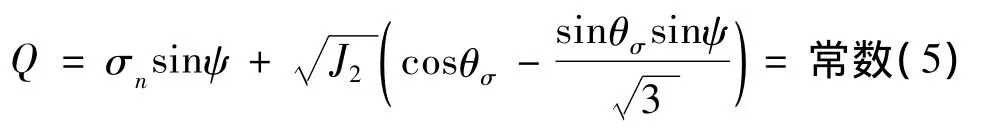
式中:σn为平均应力;ψ为剪胀角，且0≤ψ≤φ，当ψ=0时为无剪胀现象。

在有限元计算中当选取关联流动法则时，土体会呈现剪胀倾向，并且这种剪胀是无限制的，这不符合土体的性状，故岩土材料不适用关联流动准则。非关联流动准则不会使土体出现剪胀倾向，但其剪胀角的赋值具有很大的随意性，这会给模型土体参数与实际参数带来较大的差距，导致计算分析出现一定程度的误差。故本文选用ψ=0时无剪胀现象的情况。

3.3 渗透系数随应力场的改变

流固耦合的基本原理是应力场通过改变岩土体的孔隙体积大小和分布状况，来改变岩土体材料的渗透系数，即渗透系数随应力场发生改变，然后再影响应力场的相互作用。因此，在计算过程中需要根据孔隙率的变化不断的调整渗透系数，从而实现对流固耦合问题的数值模拟。

孔隙率与渗透系数耦合作用的经验公式［14］为:

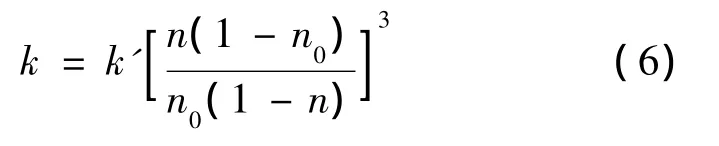
式中:n0表示土体初始孔隙率;n为变化后的孔隙率;初始孔隙率n0对应渗透系数k'，变化后的孔隙率n对应渗透系数k。

3.4 土水特征曲线

降雨入渗过程实质上是入渗水分在非饱和区运动的过程。在非饱和土中，雨水入渗会使土体饱和度增加，非饱和土含水率增大时，吸力会大幅度降低，因此在计算过程中需要考虑土水特征曲线来实现对降雨入渗问题的数值模拟。

饱和度随基质吸力的关系［15］:

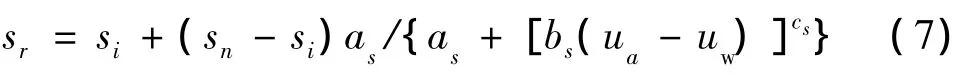
式中:sr、si和sn分别为饱和度、残余饱和度和最大饱和度;as、bs及cs均为材料系数;(ua－uw)为基质吸力。

3.5 初始条件和边界条件的确定

按照实际土坡的边界及初始条件在有限元模型建立过程中，相应定义并设置模型的初始应力、孔隙水压、饱和度和基质吸力分布、孔隙比等，基于ABAQUS进行流固耦合分析计算，对非饱和土质边坡受降雨入渗过程的影响进行研究分析。边界条件BC选项定义孔压边界条件，ABAQUS默认的是不透水边界。

4 算例分析

将土体视为均布孔隙的多孔介质，结合ABAQUS有限元软件，基于经典的Mohr－Coulomb屈服准则，对非饱和土质边坡受降雨入渗过程的影响进行应力场和渗流场的耦合分析研究。

4.1 计算模型及网格划分

本文选取一二维边坡作为耦合分析算例［16］，边坡土质均质且各向同性，坡脚为40°，坡高30 m，初始地下水位位于坡脚处，坡脚以下土层厚度为10 m。模型网格划分采用扫掠方式，网格单元属性为CPE4P耦合平面应变单元，如图2所示。

图2 有限元模型及网格图

4.2 计算参数

采用Mohr－Coulomb理想弹塑性材料模拟，表1列出了计算土坡土壤力学特性的参数。降雨过程中，排除地表形成积水的情况，视土坡模型顶面均受到降雨入渗的作用，入渗强度20 mm/h，持续时间66 h。

耦合作用是一种动态变化的过程，应力场通过改变孔隙体积进而影响了土体的渗透系数，即孔隙比(或孔隙率)的变化会导致土体渗透系数变化，公式(6)给出了渗透系数和孔隙比的变化关系，初始孔隙比取为1.0，运用该公式计算结果如表2所示。

表1 土壤各项参数

表2 渗透系数随孔隙比、孔隙率变化计算表

本例中地下水位以上的土体为非饱和土，取其最大基质吸力为－400 kPa，并且认为边坡中基质吸力从－400 kPa～0 kPa呈线性分布，饱和度随基质吸力的关系式(7)中残余饱和度si取0.08，最大饱和度 sn取1，即此时基质吸力为0 kPa，as、bs和 cs是材料系数，在本例模拟过程中分别取为1、5×10－5、3.5。把这些参数代入到式(7)中，得到如图3土水特征曲线。

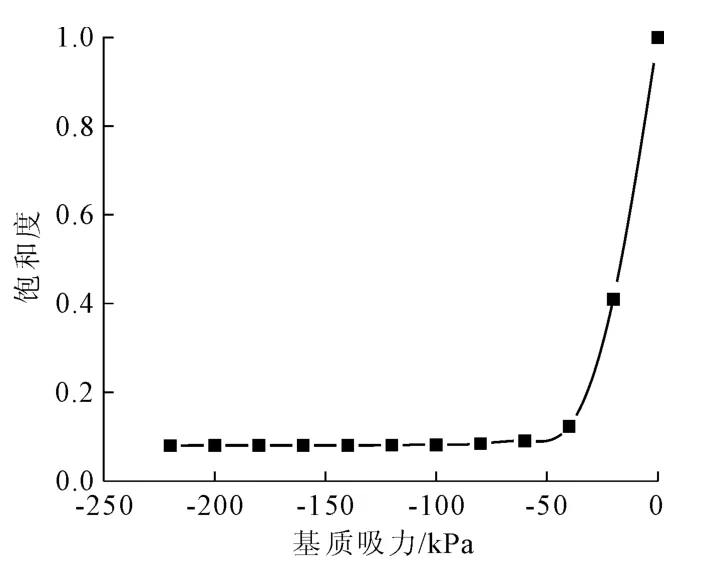
图3 土水特征曲线

4.3 边界条件和初始条件

边界条件:本例考虑降雨入渗过程的第二种情况，即降雨强度小于土壤允许入渗容量，全部雨水渗入土体，坡面为流量边界。

模型左右两侧不透水，只有沉降而无水平位移;底部边界不透水，亦无水平和竖向位移;除位移约束外，还需设置孔压边界条件，利用Distribution空间函数设置左右边界沿深度线性增加的孔压。其余边界暂设为不排水边界，不做额外的修改。

初始条件:按照实际土坡的边界及初始条件在有限元模型建立过程中，相应定义并设置模型的初始应力、孔隙水压、饱和度和基质吸力分布、孔隙比等，基于ABAQUS进行流固耦合分析计算，得到土体的初始状态，对非饱和土质边坡受降雨入渗过程的影响进行研究分析。

4.4 结果分析

4.4.1 孔压分析

由孔压水头分布云图4～图6可见，初始孔压力水头分布与考虑降雨入渗后的孔压分布有着很大的区别，考虑降雨入渗后，边坡顶部以下的吸力区范围随着降雨时间的增长而逐渐缩小，基质吸力也相应减小。对比降雨48 h和72 h后的孔压水头分布云图可以看出随着降雨时间的增长，边坡土体孔隙水压及饱和度均增大，斜坡地表浅层的基质吸力则相应减小甚至消失。可以预见，在降雨停止之后，边坡土体的孔隙水压及饱和度会随着时间的推移而逐渐减小，斜坡地表浅层的基质吸力又会逐渐增大。

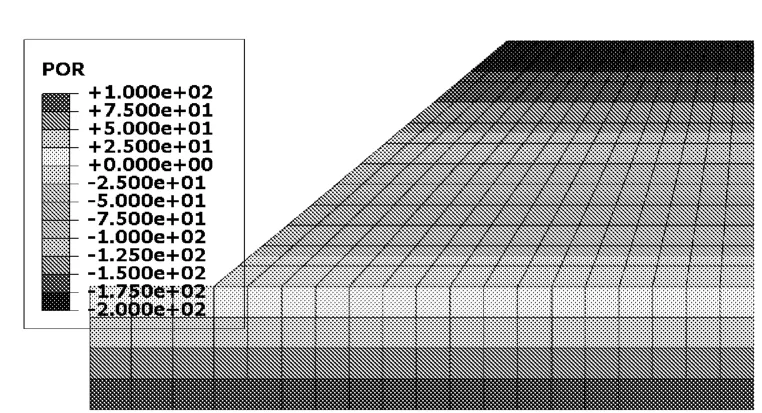
图4 初始孔压力水头分布(kPa)

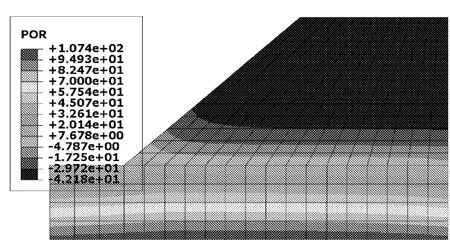
图5 降雨48 h后的孔压水头分布(kPa)

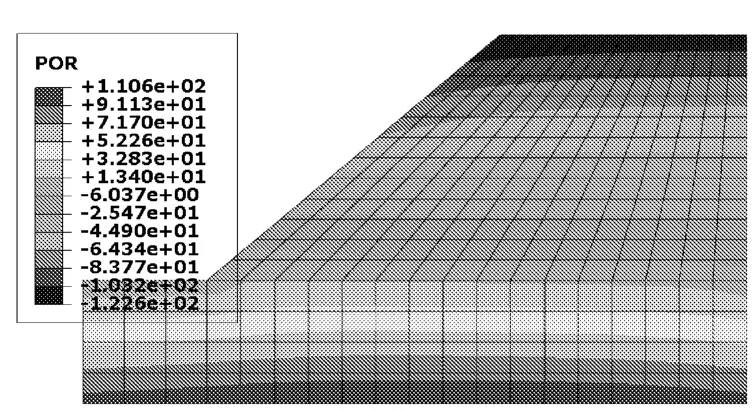
图6 降雨72 h后的孔压水头分布(kPa)

4.4.2 饱和度分析

由图7初始饱和度分布云图可见，水位以下饱和度为1，水位以上快速的减小为0.08。对比48 h和72 h的图8、图9可以发现随着降雨时间的延长，水位以上非饱和土的饱和度不断增加，在降雨减小或停止之后，边坡土体饱和度随着时间的推移又逐渐减小。

4.4.3 变形分析

图10和图11分别给出了t=72 h的水平位移和沉降的等值线图，由图10、图11可见，最大水平位移发生在坡脚，为9.547 mm;最大沉降发生在土坡中部，为4.063 mm。由图12降雨72 h后的位移矢量图分析可得，边坡在降雨入渗条件下发生滑动变形，即边坡产生不稳定性趋势。

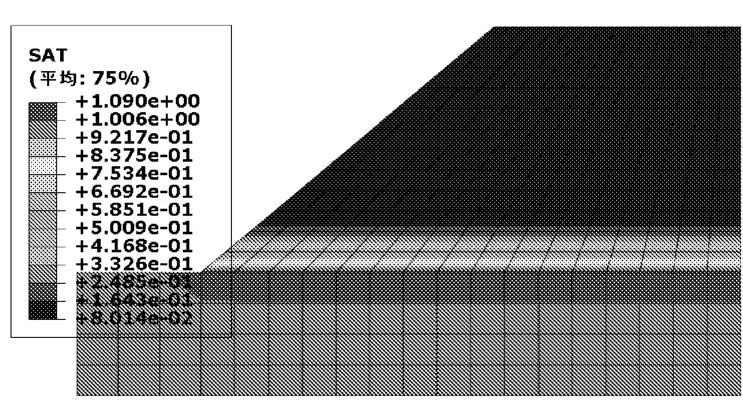
图7 初始饱和度分布

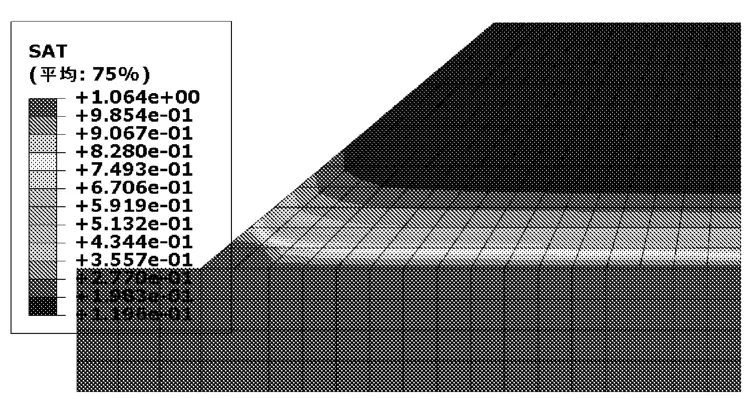
图8 降雨48 h后的饱和度分布

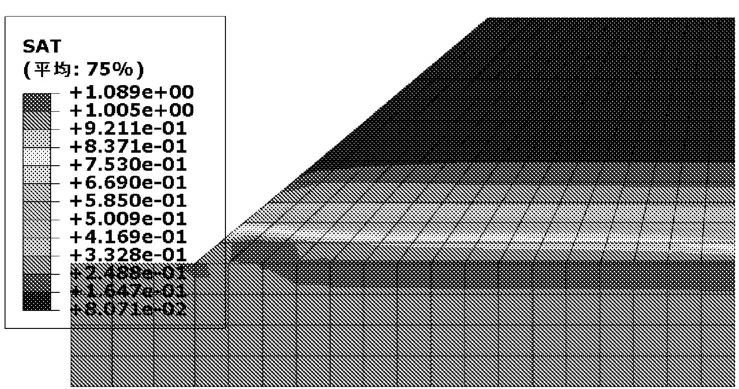
图9 降雨72 h后的饱和度分布

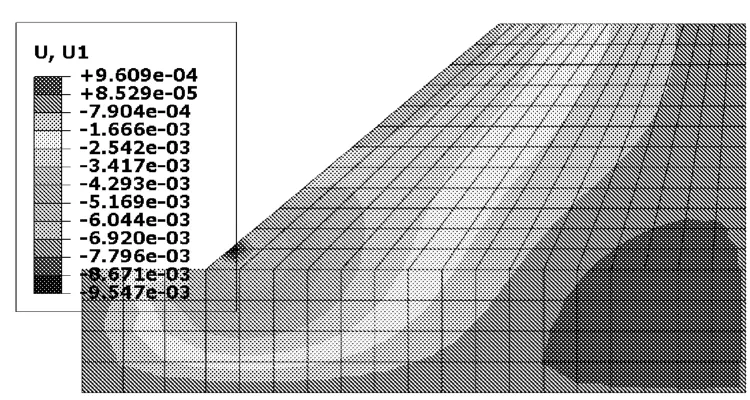
图10 降雨72 h后边坡水平位移(m)

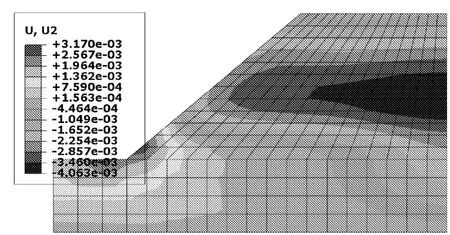
图11 降雨72 h后边坡沉降(m)

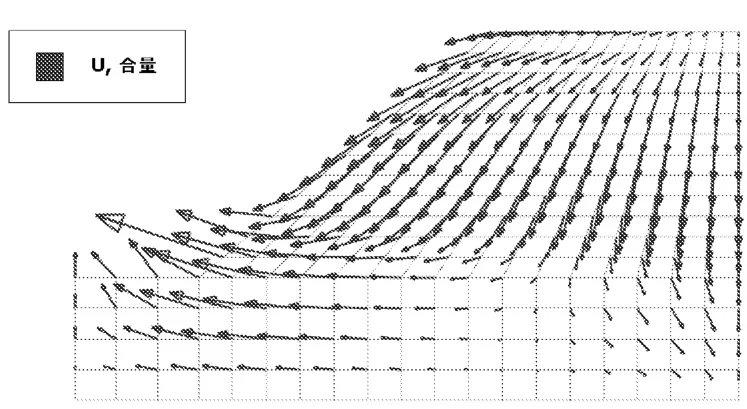
图12 降雨72 h后边坡位移矢量图

4.4.4 塑性区的发展分析

由图13、图14降雨23 h和降雨72 h的等效塑性应变云图可见，降雨入渗过程中土坡坡脚浅层最先出现塑性区，并沿坡面向上发展。等到塑性区贯通，即土坡滑动失稳破坏。

图13 降雨23 h后的等效塑性应变

图14 降雨72 h后的等效塑性应变

5 结论

本文基于ABAQUS有限元分析软件，考虑了流固耦合和土水特征曲线，结合一典型非饱和土质边坡算例，对非饱和土质边坡受降雨入渗过程的影响进行了有限元数值模拟研究，结合孔压水头分布云图得到以下结论:

(1)坡脚水位以下孔压为正值、饱和度为1，坡脚水位以上孔压为负值、饱和度快速递减，这与地下水位以上为非饱和区土体这一情况相符合，说明考虑了流固耦合和土水特征曲线的有限元模拟是符合实际的。

(2)降雨会使非饱和区形成暂态饱和区，随着降雨时间的延长，边坡土体非饱和区含水率逐渐增大，吸力相应减小。在降雨结束后，边坡土体非饱和区的饱和度随着时间的推移会不断降低，斜坡地表浅层的基质吸力又会逐渐增大。

(3)由位移矢量图和等效塑性应变图可以看出降雨会使边坡滑动变形，甚至失稳破坏。

(4)降雨入渗过程中土坡坡脚浅层最先出现塑性区，并沿坡面向上发展。因此，在保护非饱和土质边坡措施方面，坡面防水的重要性可能高于边坡排水。

(5)降雨对土质边坡物理力学特性的影响是明显的，边坡工程设计中应该对雨水入渗有足够的重视。

以上结论的得出说明考虑了流固耦合和土水特征曲线的有限元模拟是合理的、切合实际的。因此，为了更真实的分析降雨入渗过程对土质边坡的影响、更好地服务于工程设计，在常规边坡设计分析计算中应考虑降雨入渗以及耦合作用的影响。

［1］Papagiannakis A T，Fredlund D G.A steady state model forflow in satured-unsatured soils［J］. Canadian Geotechnical Journal，1978，15(3):313-321.

［2］Lumbp.Effect of rainstorm on slope stability［C］//Proceedings of Symposium on Hong Kong Soils.Hong Kong:Hong Kong University Press，1962:73-87.

［3］孙冬梅，朱岳明，张明进.降雨人渗过程的水－气二相流模型研究［J］.水利学报，2007，38(2):150-156.

［4］荣 冠，张 伟，周创兵.降雨人渗条件下边坡岩体饱和非饱和渗流计算［J］.岩土力学，2005，26(10):1545-1550.

［5］王 彦.降雨入渗对边坡稳定的影响［D］.南京:河海大学，2001.

［6］芮孝芳.产流模式的发现与发展［J］.中国农村水利水电，2013(5):105-112.

［7］赵 江.路基路面在降雨条件下渗流分析及边坡稳定性研究［D］.昆明:昆明理工大学，2005:17-23.

［8］徐 晗，朱以文，蔡元奇，等.降雨入渗条件下非饱和土边坡稳定分析［J］.岩土力学，2005，26(12):1958-1962.

［9］张子达.边坡降雨入渗的力学特性分析［J］.中外公路，2007，27(2):27-30.

［10］李宗坤，陈丽刚，韩立炜.基于ABAQUS渗流与应力耦合的边坡稳定性分析［J］.人民黄河，2011，33(2):103-104.

［11］朱以文，蔡元奇，徐 咯.ABAQUS与岩土工程分析［M］.香港:中国图书出版社，2005.

［12］张晓咏，戴自航.应用ABAQUS程序进行渗流作用下边坡稳定分析［J］.岩石力学与工程学报，2010，29(S1):2930-2931.

［13］林 嵩.降雨入渗过程中的土质边坡稳定分析［D］.大连:大连理工大学，2008.

［14］孙 锋.堤坝劈裂灌浆的流固耦合分析［D］.青岛:山东科技大学，2007.

［15］陈锡阳.基于ABAQUS的真空联合堆载预压软基固结分析［D］.湘潭:湘潭大学，2011.

［16］费 康，张建伟.ABAQUS在岩土工程中的应用［M］.北京:中国水利水电出版社，2010.