负弯矩作用下钢-混凝土组合箱梁畸变屈曲分析*
2015-12-19周旺保蒋丽忠李书进孔凡
周旺保 蒋丽忠 李书进 孔凡
(1.武汉理工大学 土木工程与建筑学院,湖北 武汉430070;2.中南大学 土木工程学院,湖南 长沙410075)
钢-混凝土组合箱梁由钢梁通过抗剪连接件与混凝土板形成整体,共同承受外部荷载的作用.在实际楼板结构中,因为混凝土翼缘板的抗扭刚度和侧向刚度很大,所以在组合箱梁的负弯矩区域,钢梁受到混凝土板侧向和扭转约束作用.钢梁底板在承受较大的不利分布荷载发生屈曲时,产生侧向变形的同时伴随着钢梁腹板的横向变形,即畸变屈曲,因此畸变屈曲为负弯矩作用下钢-混凝土组合箱梁的主要屈曲模式.
目前,对钢-混凝土组合梁稳定性能的研究一般采用数值计算方法或简化理论计算方法.Lee、Vrcelj 等[1-2]利用数值方法分别对普通工字钢连续梁和组合连续梁非线性基本屈曲性能进行了研究,并进行了参数分析.聂建国等[3]运用瑞利-里兹能量法推导出了翼板完全断开的工字钢混凝土组合梁侧扭失稳模式的临界弯矩计算公式.Ye 等[4-5]以弹性地基压杆弯扭屈曲代替工字钢约束畸变屈曲的方法对工字钢组合梁畸变屈曲性能进行了研究,并指出弹性地基梁法比能量变分法更为合理.Svensson、Williams 等[6-8]相继对弹性地基梁方法进行了拓展,如增加楼板刚度贡献和腹板参与面积等.周旺保等[9-10]对工字钢-混凝土组合梁的腹板转动和侧向约束刚度进行了深入研究,获得了工字钢-混凝土组合梁畸变屈曲高精度解析解.刘沐宇等[11]采用能量变分法构建了剪切应力作用下考虑弹性转动约束边界的工字钢-混凝土组合梁高腹板的临界屈曲应力计算模型,基于弹性薄板理论分析了混凝土桥面板、剪力钉、钢翼缘板结构特性、材料参数与边界弹性转动约束系数之间的关系.童根树等[12]采用能量法获得了工字钢-混凝土组合梁下翼缘弹性畸变屈曲临界应力,并在大量数值计算基础上获得了工字钢-混凝土组合梁畸变屈曲临界荷载的实用计算公式.
上述研究对象基本为工字钢-混凝土组合梁,对于钢-混凝土组合箱梁畸变屈曲方面的研究尚不多见.文献[13-16]的研究表明:纯弯矩作用下组合梁畸变屈曲临界荷载计算方法是变轴力作用下畸变屈曲临界荷载计算方法的基础.本研究对负弯矩区组合箱梁底板的转动及侧向约束刚度进行全面、深入的研究,获得钢梁底板转动及侧向约束刚度的计算方法,在此基础上进一步推导负弯矩作用下组合箱梁畸变屈曲临界弯矩计算公式,最后结合15 个算例对文中简化计算方法的精度进行分析及讨论.
1 基本假定
钢-混凝土组合箱梁基本尺寸见图1,组合箱梁与普通钢梁的侧向失稳模式不同,组合箱梁中钢梁上翼缘嵌在侧向和扭转刚度较大的混凝土板内,钢梁侧向变形和扭转变形都受到混凝土板的约束.因此,组合箱梁的屈曲失稳为伴随钢梁腹板侧向弯曲变形的弯扭畸变屈曲.

图1 钢-混凝土组合箱梁截面尺寸Fig.1 Section dimensions of steel-concrete composite box beams
为了简化计算,文中做如下假定[12-18]:
(1)混凝土板的侧向弯曲刚度及扭转刚度相对较大,钢梁上翼缘受到混凝土板的约束不能发生侧向和扭转变形;
(2)不考虑混凝土的抗拉能力;
(3)钢梁底板两侧受钢梁腹板的竖向约束作用很大,即取钢梁底板竖向约束刚度ky= ∞.
根据上述基本假定,组合箱梁畸变屈曲模型可简化为水平和扭转方向受弹簧约束、竖向受刚性约束的薄板约束扭转问题,其简化计算模型如图2所示.
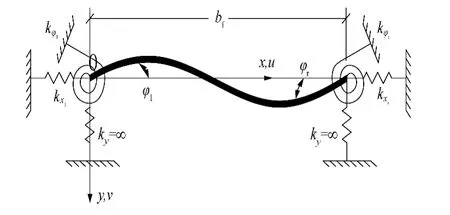
图2 钢-混凝土组合箱梁简化计算模型Fig.2 Simplified calculation model of steel-concrete composite box beams
2 钢梁腹板约束刚度的推导
2.1 钢梁腹板转动约束刚度的推导
钢梁腹板下缘发生转动时,腹板两横向边简支,与上翼缘交接边固支,与底板交接边简支.钢梁腹板屈曲变形边界条件可表示为[9-10]
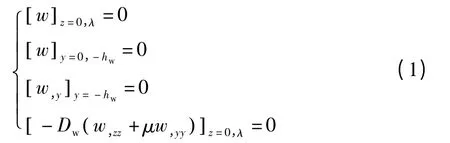
式中:Dw= Et3w/12 (1 - μ2) ,其中μ 为钢材泊松比,E 为钢材弹性模量,tw为钢梁腹板厚度;w 为腹板屈曲变形函数;hw为钢梁腹板高度;λ = l/n,其中n为屈曲半波数,l 为组合箱梁长度.
钢梁左腹板侧向变形可用三次函数f1(y) 和三角级数进行模拟,表达式如下[15-16]:

式中:cl为左腹板屈曲变形广义坐标.
根据上述边界条件,f1(y) 可表示为
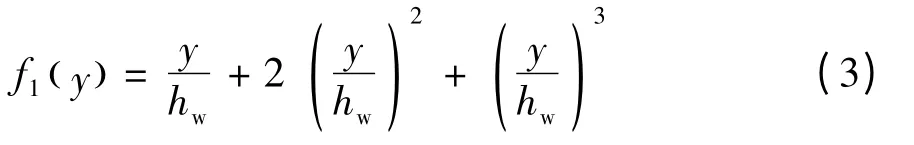
因此,钢梁左腹板屈曲变形函数可表示为[15-16]

在考虑混凝土板翼缘钢筋后,腹板下边缘处轴向压应力为

式中,yc为组合箱梁等效截面形心至坐标原点距离,Af为钢梁底板横截面积,At为钢梁上翼缘横截面积,Aw为钢梁腹板横截面积,As为混凝土钢筋面积,ys为钢筋形心至钢梁底板的距离,Mx(z) 为作用在组合梁上的负弯矩值,I 为组合箱梁截面惯性矩.
根据势能驻值原理可得[15-16]

根据弹性薄板理论可知钢梁左腹板所受的侧向分布力为[15]

同理,可得

式中,kφr,1为钢梁右腹板的转动约束刚度,cr为右腹板屈曲变形广义坐标,fx,φr为钢梁右腹板所受的侧向分布力.
2.2 钢梁腹板侧向约束刚度的确定
钢梁腹板下缘发生侧向移动时,腹板两横向边简支,与上翼缘交接边固支,与底板交接边可侧向移动.钢梁腹板屈曲变形边界条件可表示为[9-10]

钢梁左腹板/右腹板侧向变形可用三次函数和三角级数进行模拟,表达式如下[15-16]:

根据上述边界条件,f2(y) 可表示为[15-16]
田间性能试验在位于山东省临沂市莒南县道口乡烟苗育苗区进行,试验地为一处标准化育苗大棚。烟苗品种为K326,烟苗生长期为竖膀期,株高约7~8cm。消毒液为30%有效氯的漂白粉10~20倍稀释液。剪叶操作按农艺要求,剪切位置在烟苗生长点以上,对大叶1/3处进行水平剃剪,每剪10盘烟苗对切刀和壳体内腔消毒1次;在切刀旋转状态下打开消毒容器开关约20s后再关闭,停机消毒,消毒时间不低于2min。
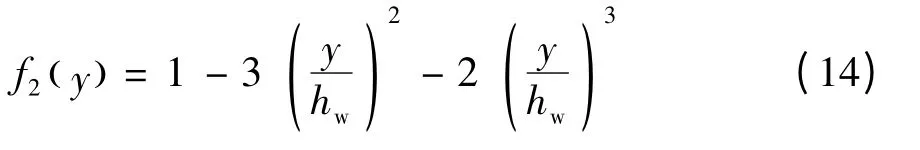
因此,钢梁左腹板/右腹板屈曲变形函数可表示为

根据势能驻值原理可得[15-16]

式中,kx为钢梁左腹板/右腹板的侧向约束刚度,d为左腹板/右腹板屈曲变形广义坐标,

根据弹性薄板理论可知此时左腹板/右腹板所受的侧向分布弯矩为[15]

3 组合箱梁弯扭畸变屈曲临界弯矩
3.1 临界弯矩的推导
如图2所示,设钢梁底板水平侧向位移为u,钢梁底板平面外屈曲变形函数为v,左端转角为φl,右端转角为φr.钢梁底板屈曲变形的边界条件为[15-16]

钢梁底板变形函数可用三角函数进行模拟,表达式如下:

根据变形协调,可取[15-16]


钢梁底板的位移函数可表示为


式中,Iy=tfb3f/12 ,tf为底板厚度,bf为底板宽度,分别为钢梁底板左侧/右侧转动约束刚度,kx= - kx1为钢梁底板的侧向约束刚度.
根据腹板与底板的变形协调,钢梁底板的左端转角、右端转角及侧向位移可表示为

将式(27)代入式(24)、(25)和(26)后,根据伽辽金法[19]可得


η 为组合箱梁屈曲变形向量,η = (cl,cr,d)T.
3.2 临界屈曲荷载计算方法
因为所取的腹板及底板屈曲变形函数往往不可能是组合箱梁真实的屈曲变形,这就相当于增加了约束才可能使其实现,因此提高了所得的组合箱梁畸变屈曲临界荷载.为消除误差,将钢梁底板转动约束刚度乘以折减系数ζ 进行折减.联立式(7)、(10)、(16)及(28)可得

式中,B = ζB0+B1,N = ζN0+N1,H = 2H0+H1,S = 2S0+ S1.
当组合箱梁发生畸变屈曲时,变形向量η 不能为零,此时组合箱梁畸变屈曲问题可以转化为下式所示的特征矩阵的广义特征值问题:

求解式(30)可得 3 个广义特征值σti(i = 1,2,3),取σcr即为组合梁弯扭临界屈曲特征应力.组合箱梁畸变屈曲临界弯矩可由下式进行计算:

4 参数分析和算例
钢-混凝土组合箱梁截面尺寸示意图如图1所示,各算例基本几何尺寸如表1所示.
利用有限元法对各算例在负弯矩作用下的畸变屈曲临界弯矩进行计算;同时变化钢梁底板转动约束刚度折减系数,采用不同的转动约束刚度折减系数对各算例畸变屈曲临界弯矩进行计算,以获得合适的钢梁底板转动约束刚度折减系数.有限元分析利用ANSYS 软件实现:混凝土板以侧向约束代替,即在进行屈曲分析时约束钢梁上翼缘x 方向及y 方向的平动,模拟混凝土板对钢梁的侧向及转动约束;钢梁部分采用SHELL43 单元模拟,弯矩以应力梯度方式施加,钢梁端部所有节点均约束其x 方向及y 方向的平动,限制端部的侧向及扭转变形,右侧再取一个节点,约束其纵向平动自由度,以满足组合箱梁构件静定要求同时允许截面沿弯矩作用方向发生转动.ζ = 0.5 时,文中计算方法与有限元计算方法比较结果如表2所示.

表1 组合箱梁算例基本几何尺寸Table1 Basic geometric size of composite box beams mm

表2 负弯矩作用下组合箱梁畸变屈曲临界弯矩Table2 Distortional buckling critical moment of composite box beam under negative moment
由表2可知,当取ζ = 0.5 时,15 个算例平均误差为0.63%,误差方差为0.000 011 2,说明取ζ =0.5 时,文中计算方法能取得较好的精度.转动约束刚度折减系数取不同值时的误差分析如图3所示.
从图3可以看出:转动刚度折减系数取0.5 时,计算精度较高;随着折减系数偏离0.5 的幅度增大,计算精度减小,建议取折减系数为0.5.
从表2及图3可以看出:在负弯矩作用下,同截面组合箱梁畸变屈曲临界弯矩受构件的长度影响较小;转动约束刚度折减系数取0.5 时,式(31)与有限元计算方法吻合良好,建议取折减系数为0.5.

图3 转动约束刚度折减系数参数分析Fig.3 Parameter analysis of the reduction coefficient of rotating restraint stiffness
5 结论
文中对组合箱梁钢梁底板侧向约束刚度kx和转动约束刚度kφ进行了深入的研究,进一步获得了组合箱梁畸变屈曲临界弯矩的计算方法,并通过实例与现有计算方法相比,得到以下主要结论:
(1)钢梁底板转动约束刚度kφ及侧向约束刚度kx均与纵向压应力呈耦合关系.
(2)在负弯矩作用下,同截面组合箱梁畸变屈曲临界弯矩受构件的长度影响较小.
(3)在负弯矩作用下,转动约束刚度折减系数取0.5 时,文中方法的结果与有限元计算方法结果吻合良好,上下波动不超过2%,证明了文中计算方法的有效性.该分析方法为进一步获得组合箱梁变轴力作用下临界弯矩的实用计算公式提供了理论基础.
[1]Lee D S.Inelastic lateral-distortional buckling of continuously restrained continuous beams [J].Steel and Composite Structures,2005,5(4):305-326.
[2]Vrcelj Z,Bradford M A.Inelastic restrained distortional buckling of continuous composite T-beams[J].Journal of Constructional Steel Research,2009,65(4):850-859.
[3]聂建国,王宇航,蔡奇.翼板开洞率100%的钢-混凝土组合梁整体弹性稳定性分析[J].工程力学,2010,27(6):51-56.Nie Jian-guo,Wang Yu-hang,Cai Qi.Elastic lateral stability analysis of composite steel-concrete beams with whole openings in concrete slab [J].Engineering Mechanics,2010,27(6):51-56.
[4]Ye J H,Chen W.Elastic restrained distortional buckling of steel-concrete composite beams based on elastically supported column method [J].International Journal of Structural Stability and Dynamics,2013,13(1):1-29.
[5]叶继红,陈伟.工字钢-混凝土组合梁弹性约束畸变屈曲研究[J].建筑结构学报,2011,32(6):82-91.Ye Ji-hong,Chen Wei.Elastic restrained distortional buckling of I-steel-concrete composite beams[J].Journal of Building Structures,2011,32(6):82-91.
[6]Svensson S E.Lateral buckling of beams analysed as elastically supported columns subject to a varying axial force[J].Journal of Constructional Steel Research,1985,5(3):179-193.
[7]Williams F W,Jemah A K.Buckling curves for elastically supported columns with varying axial force,to predict lateral buckling of beams [J].Journal of Constructional Steel Research,1987,7(2):133-147.
[8]Goltermann P,Svensson S E.Lateral distortional buckling:Predicting elastic critical stress [J].Journal of Structural Engineering,1988,114(7):1606-1625.
[9]周旺保,蒋丽忠,邵光强,等.钢-混凝土组合梁负弯矩区弹性畸变屈曲分析[J].中南大学学报:自然科学版,2012,43(6):2316-2323.Zhou Wang-bao,Jiang Li-zhong,Shao Guang-qiang,et al.Elastic distortional buckling analysis of steel-concrete composite beams in negative moment region[J].Journal of Central South University:Science and Technology,2012,43(6):2316-2323.
[10]周旺保,蒋丽忠,余志武.钢-混凝土组合梁负弯矩区畸变屈曲弯矩计算公式[J].计算力学学报,2012,29(3):446-451.Zhou Wang-bao,Jiang Li-zhong,Yu Zhi-wu.The distortional buckling calculation formula of the steel-concrete composite beams in the negative moment region [J].Chinese Journal of Computational Mechanics,2012,29(3):446-451.
[11]刘沐宇,陈齐风,张强.弹性转动边界约束的组合梁腹板剪切屈曲分析[J].华中科技大学学报:自然科学版,2014,42(1):84-88.Liu Mu-yu,Chen Qi-feng,Zhang Qiang.Wed plate buckling analysis in steel-concrete composite girder considering elastic rotational restraint boundary under shear[J].Journal of Huazhong University of Science and Technology:Natural Science Edition,2014,42(1):84-88.
[12]童根树,夏骏.工字形截面钢连续梁负弯矩区的稳定性[J].建筑钢结构进展,2007,9(1):46-51.Tong Gen-shu,Xia Jun.Buckling of I-sectional steel beams loaded by negative moments [J].Progress in Steel Building Structures,2007,9(1):46-51.
[13]童根树,夏骏.工字形截面框架梁负弯矩区的弹性侧向稳定分析[J].建筑结构,2006,36(S1):390-394.Tong Gen-shu,Xia Jun.Elastic lateral stability analysis of I-sec frame beam in negative moment zone [J].Building Structures,2006,36(S1):390-394.
[14]Chen Shi-ming,Jia Yuan-lin.Numerical investigation of inelastic buckling of steel-concrete composite beams prestressed with external tendons[J].Thin-Walled Structures,2010,48(3):233-242.
[15]Zhou Wang-bao,Jiang Li-zhong,Kang Jun-tao,et al.Distortional buckling analysis of steel-concrete composite girders in negative moment area[J].Mathematical Problems in Engineering,2014,2014:635617.
[16]Jiang Li-zhong,Qi Jing-jing,Scanlon A,et al.Distortional and local buckling of steel-concrete composite boxbeam [J].Steel and Composite Structures,2013,14(3):243-265.
[17]贾远林,陈世鸣.钢-混凝土组合梁在负弯矩作用下的屈曲失稳系数研究[J].工程力学,2009,26(11):121-126.Jia Yuan-lin,Chen Shi-ming.Buckling coefficient of steel-concrete composite beams in negative bending[J].Engineering Mechanics,2009,26(11):121-126.
[18]刘洋,童乐为,孙波,等.负弯矩作用下钢-混凝土组合梁受力性能有限元分析及受弯承载力计算[J].建筑结构学报,2014,35(10):10-20.Liu Yang,Tong Le-wei,Sun Bo,et al.FEA and bending capacity calculation for mechanical behavior of steel-concrete composite beams under negative moment[J].Journal of Building Structures,2014,35(10):10-20.
[19]Tinh Quoc Bui,Minh Ngoc Nguyen.Meshfree Galerkin Kriging model for bending and buckling analysis of simply supported laminated composite plates [J].International Journal of Computational Methods,2013,10(3):1350011.
