非饱和土中部分埋入桩的竖向振动*

章敏 王星华 冯国瑞 梁燕

(1.太原理工大学 建筑与土木工程学院，山西 太原030024;2.中南大学 土木工程学院，湖南 长沙410075)

随着我国交通和能源等基础建设的发展，部分埋入式桩基础被广泛应用于山区(或深水)桥梁、海上平台以及离岸码头等结构中.与传统的全埋入式桩基础相比，桩顶自由段的存在使部分埋入桩具有更小的承载力和动力阻抗，在较大竖向或复杂荷载条件下甚至发生压屈失稳破坏.探讨部分埋入桩在振源(列车、风电机组等)运营或工作期间的动力响应对保证上部结构安全和正常工作具有重要的学术和工程应用价值.

在国外，有关部分埋入桩动力响应的研究大多集中在桩的自由振动特性和自振模态上.Lee 等［1］基于Winkler 地基假定，对部分埋入变截面桩的自振特性进行了研究;Catal、Yusuf 等［2-4］通过引入变形曲线的二阶导数来反映桩的剪切效应，推导了单层和双层地基中部分埋入桩在弯矩和剪力作用下自振频率的非平凡解，讨论了自由段长度、边界条件和截面形状因子的影响.Sapountzakis 等［5］考虑剪切变形和转动惯量，采用边界元法对任意荷载作用下部分埋入Timoshenko 梁进行了非线性动力分析.近些年，国内学者对这一问题也做了进一步研究.任青等［6-7］基于传递矩阵法和桩- 桩相互作用因子，探讨了成层土中部分埋入群桩以及柔性高承台群桩的竖向动力阻抗;在此基础上，钟锐等［8］将该问题推广到了非线性土体的情况;此外，余云燕等［9］从损伤检测的角度，采用回传射线矩阵法对部分埋入缺陷桩在半正弦脉冲作用下的频域及时域响应进行了分析.

以上研究主要针对单相介质土情况，而天然土层大多为固、液、气三相混合物，孔隙水与土骨架间存在着相对运动，并受到空气含量的影响.饱和度的变化将引起土体基质吸力、有效应力等性质发生一系列的改变，研究符合实际土体环境下的桩土动力相互作用问题应当考虑土体的三相耦合效应.张智卿等［10-11］在忽略孔隙气体的单相流基础上，首次推导了简化条件下非饱和土层中端承桩在半正弦脉冲激励作用下的时域响应解答，但所采用的波动方程仍属于两相介质模型，无法考虑毛细压力作用，具有一定的局限性.借助唯象理论，徐明江［12］建立了三相多孔介质的波动方程，并就非饱和地基上薄板竖向振动的混合边值问题进行了分析.从已有文献来看，桩在单相和饱和两相介质中的动力响应研究已较为成熟，在理论分析、试验测试、数值模拟等方面均取得了许多公认的成果，有关非饱和土-桩动力相互作用的研究则尚处于起步阶段.

基于以上背景，本研究从三相多孔介质波动方程出发，充分考虑不同相之间的耦合效应和毛细压力作用，在求得自由场竖向位移和剪应力分布的基础上，结合半埋入桩上下区域的连续性条件和桩端弹性支承假定，导出了竖向稳态谐振下部分埋入单桩阻抗函数的封闭形式解答，分析了饱和度和自由段长度对桩-土系统动力响应的影响;以期为后续研究部分埋入群桩基础的振动特性提供理论基础.

1 计算模型与边界条件

1.1 计算模型与基本假定

非饱和土中部分埋入桩受竖向简谐振动的计算模型如图1所示.假定柱形坐标系统(r，θ，z)的z 轴与桩身轴线相一致，坐标原点位于自由段与埋入段的分界处.桩为等截面、均质弹性圆杆，桩端和土层底部简化为弹性支承，自由段桩长为L1、埋入段桩长为L2，半径为r0、弹性模量为Ep、密度为ρp，土层底部和桩端地基反力系数分别为ks、kb.桩顶作用一竖向激振力P(t)=P0eiωt，埋入段每延米的桩侧摩阻力为f(z).

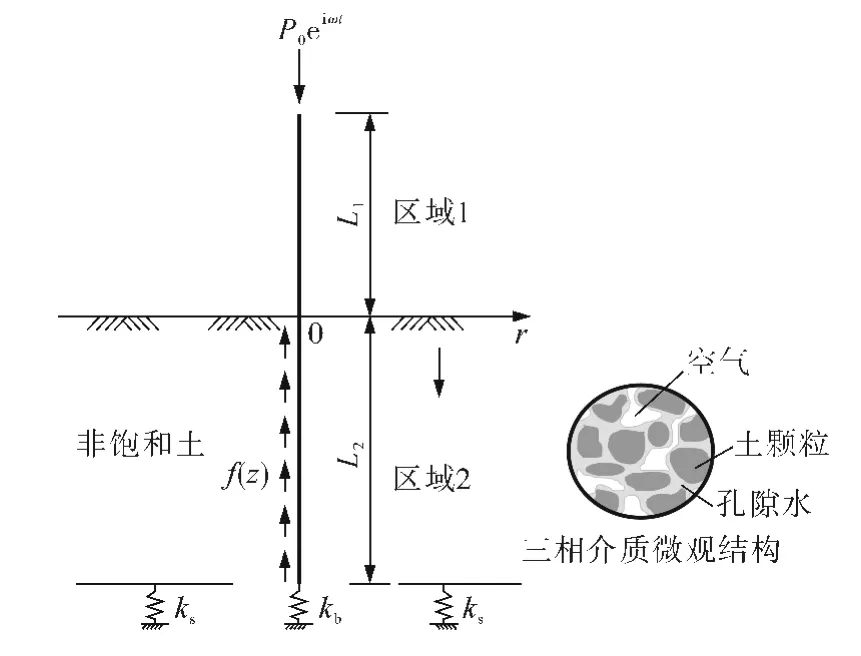
图1 非饱和土中部分埋入桩计算模型Fig.1 Calculation model of a partially-embedded pile in unsaturated soil

为简化计算，假定桩周土为均匀、各向同性的固、液、气三相弹性多孔介质;地表为透水和透气的自由边界;桩-土体系仅发生弹性小变形，且桩-土之间完全连续接触，不发生滑移和脱离;基桩等效为Euler 梁模型，忽略其横向变形.尽管在高承台桩的极限承载力计算中，应进行折减以考虑压屈稳定，而本研究旨在研究工作荷载条件下桩的振动特性，忽略桩身可能发生的动力屈曲失稳破坏.另外，文献［12］关于非饱和土及其波动方程的基本假定在本文中仍然适用.

需要说明的是，文中将桩端土体简化为Winkler弹性地基，弹簧刚度可近似采用非饱和地基上刚性圆盘在竖向简谐振动作用下的复刚度来代替.然而，由于问题的复杂性，仅文献［12］对此做了初步研究，但表达式过于繁琐，且未单就饱和度本身的影响进行分析.为便于应用，文中根据文献［13］提出的模拟公式，采用单向介质半空间表面刚性基础的地层动刚度表示kb，即kb=4μr0/(1 -ν)，μ 和ν 分别为土体剪切模量和泊松比.研究表明［14］，对于渗透性较好的地基，按该理论与饱和两相介质理论得到的动力柔度系数的差别并不大;此外，非饱和半空间在简谐圆盘荷载下的位移和应力分布受饱和度本身的影响很小［15］，为此文中暂且假定kb不随饱和度的影响而变化.

1.2 边界条件

(1)非饱和土层的边界条件

水平方向无限远处土体应力、应变和位移均趋近于0:

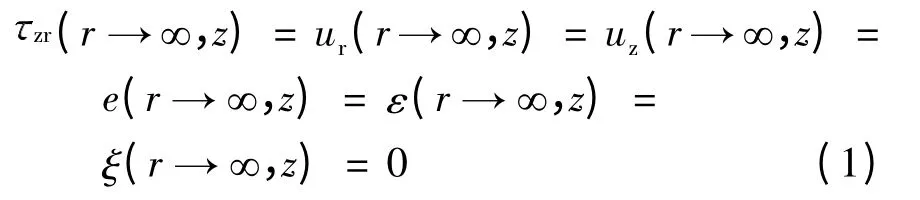
式中，zr为剪应力，ur、uz分别代表土体径向和竖向位移，e、ε 和ξ 分别为土骨架的体积应变、孔隙水及空气相对于土骨架的体积应变.

地表为透水透气边界，且正应力为0:

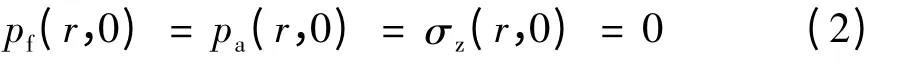
土层底部假定为弹性支承:

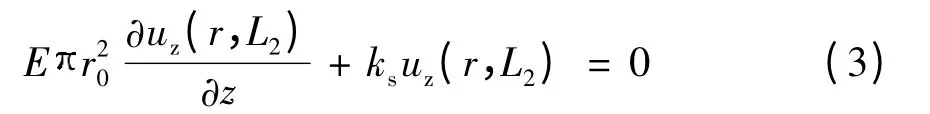
式中，E 为土体的弹性模量，与土骨架的Lame 常数λ、μ 满足

(2)桩土接触面两侧的连接条件

桩土完全接触，接触面无滑移脱离:

式中，wp为桩身竖向位移.

桩身材料密实，桩土接触面不透水、不透气:

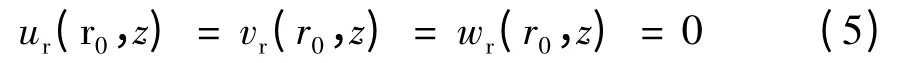
式中，vr、wr分别为孔隙水和空气的相对径向位移.

接触面上土体剪应力与桩身摩阻力相等:

(3)桩的边界条件

桩顶边界条件:

桩端边界条件:

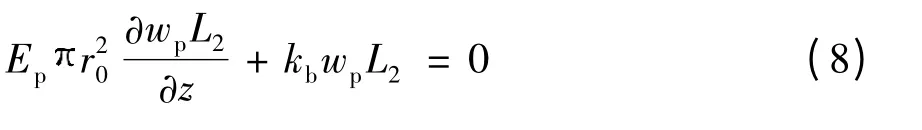
2 部分埋入桩竖向振动问题求解

2.1 控制方程

徐明江［12］根据多相孔隙材料的连续介质理论，考虑各相物质间的粘性、惯性耦合效应，以及毛细压力作用，推导了非饱和土的动力控制方程，其向量形式可表述为

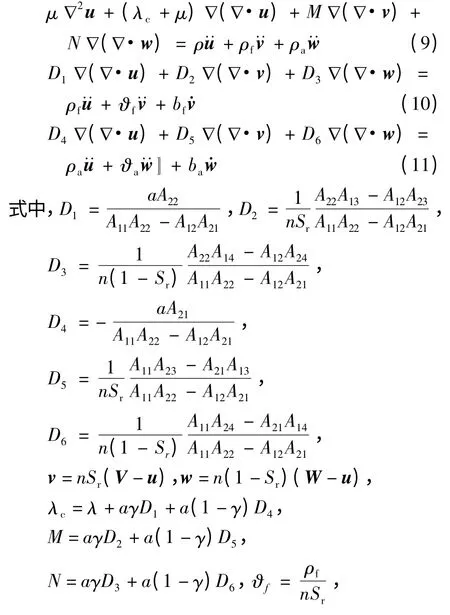
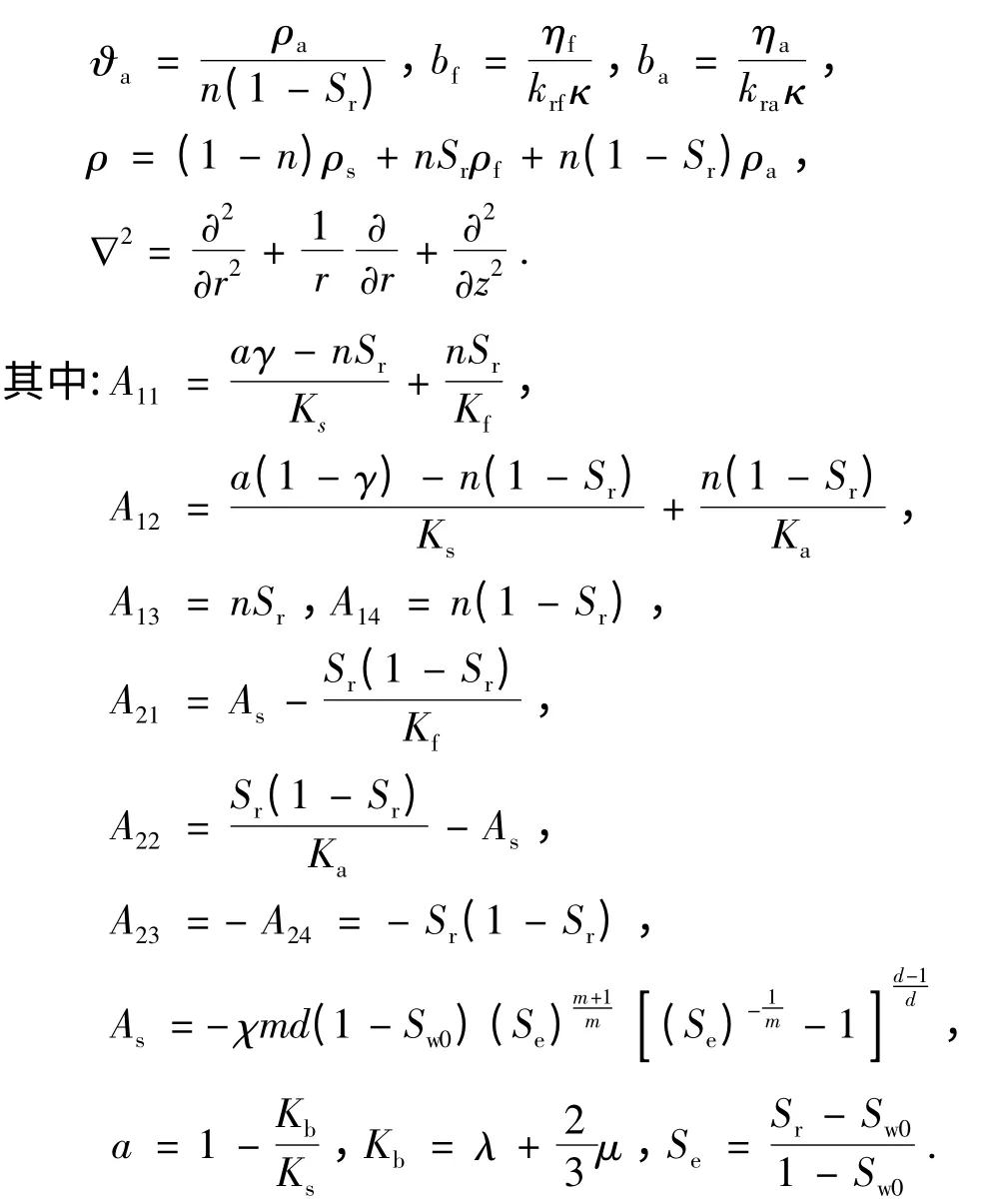
u、v 和w 分别表示固相位移矢量、水和气体相对于土骨架的位移矢量;V、W 分别表示水和空气的绝对位移;点号表示对时间的偏导;ρs、ρf、ρa和ρ 分别代表土颗粒密度、流体密度、气体密度和土体密度;Sr和Sw0为流体饱和度和束缚饱和度;γ 为有效应力系数，取决于土体饱和度、土体结构、干湿循环特性以及应力变化，可近似取γ=Sr;n 为土体孔隙率;λ 和μ 为土骨架的Lame 常数;ηf和ηa分别为流体和空气的粘滞系数;krf和kra分别为流体和空气的相对渗透系数，其表达式详见文献［15］;k 为土的固有渗透系数(m2);Ks、Kf、Ka及Kb分别是土颗粒、流体、空气及土骨架的体积压缩模量;参数As中χ、m 和d 分别为拟合参数.以上各变量中，下标符号s、f 和a 分别代表非饱和土体的固、液、气相.

2.2 非饱和土竖向振动解

考虑到桩土体系为稳态简谐振动，上述方程可略去公共时间因子eiωt(ω 为圆频率，)，同时引入如下无量纲参数和变量对方程(9)-(11)中的三式进行无量纲处理:

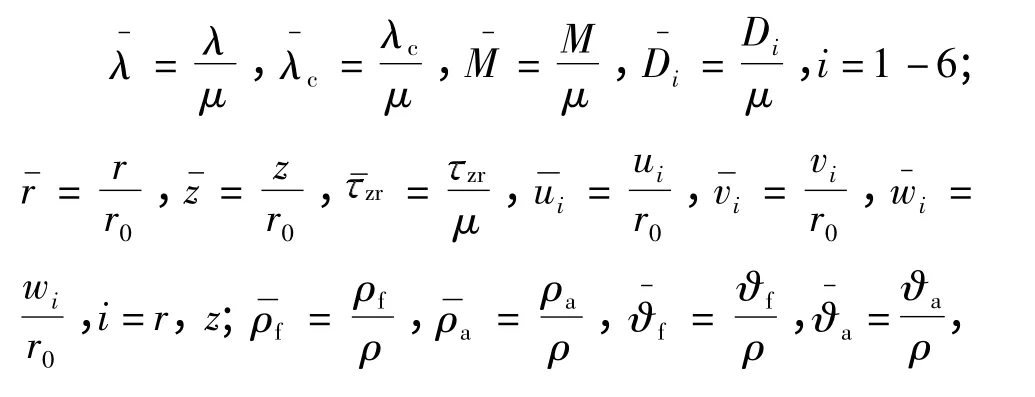
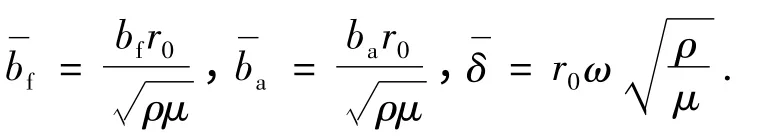
文献［16］在考虑自由场地竖向和径向波动效应的前提下，通过算子分解和分离变量法对非饱和土控制方程(9)- (11)进行解耦，求得了频域内桩-土界面的位移和剪应力，解答如下.

非饱和土层在桩-土界面处的竖向位移幅值为

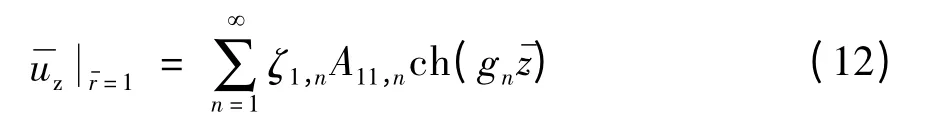
式中，ζ1，n= (g8，n/gn)K0(g8，n)+ c1，nk1，nK0(g2，n)+c2，nk2，nK0(g4，n)+ c3，nk3，nK0(g6，n).

桩周土对桩身的剪切应力幅值为

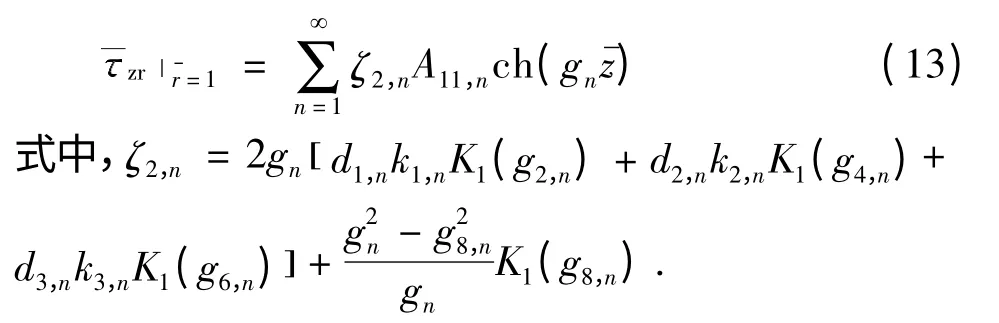
式中，K0(g)、K1(g)分别为零阶和一阶第二类修正Bessel 函数，其余变量的含义和表达式详见文献［16］.以上两式中的ζ1，n、ζ2，n是由桩土耦合振动特性以及接触面两侧的衔接条件决定的一系列系数，反映了各振动模态下桩-土的振动耦合效应.

对于桩端为弹性支承条件，由式(3)，可得gn满足如下超越方程:

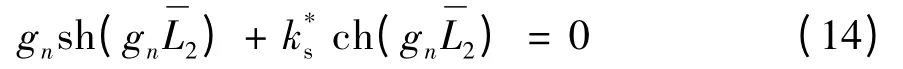
2.3 部分埋入单桩竖向振动求解

在简谐荷载作用下桩体发生强迫振动，取区域1和区域2 桩身微元体作动力平衡分析，可得桩的竖向振动方程为

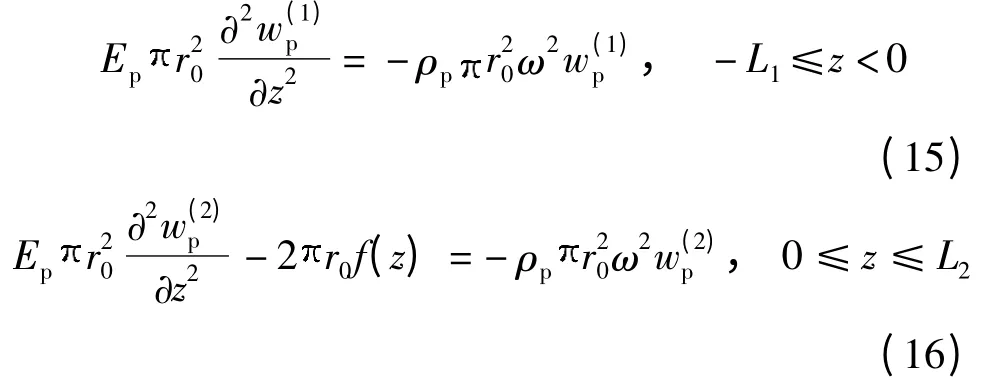
结合式(6)，以上两式可写成如下无量纲形式:

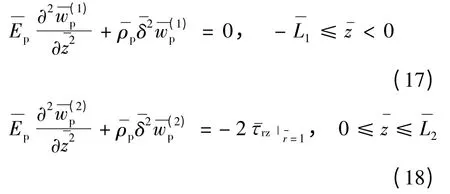
将式(13)代入式(17)-(18)，可得方程的解为

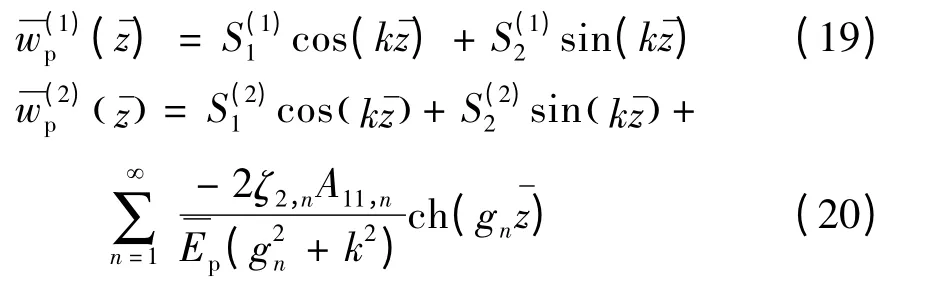
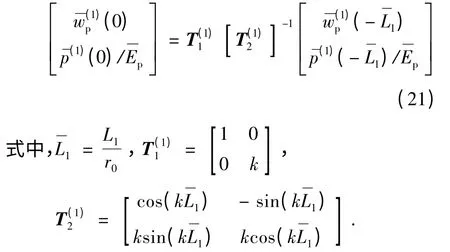
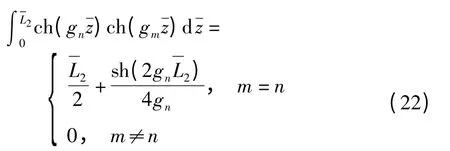
将埋入段桩身位移表达式(式(18))代入桩土分界面上的位移连续条件式(4)，可得

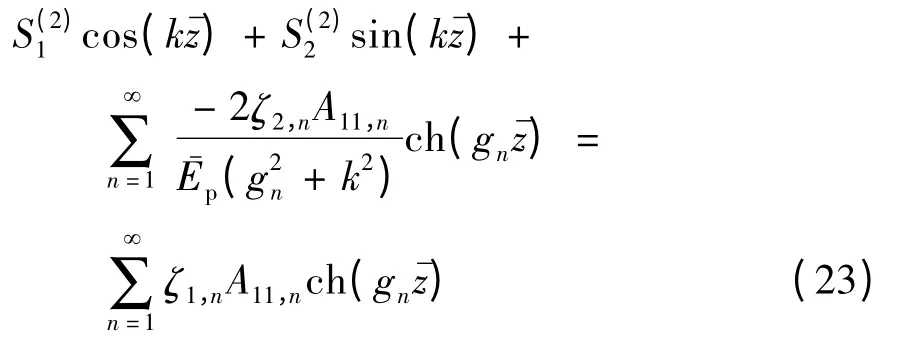
根据正交函数的性质，可得到参数A11，n的表达式为

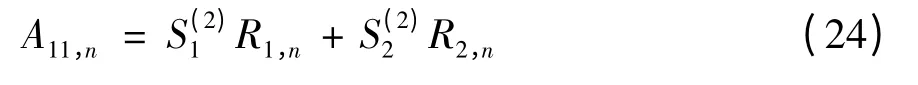
式中，

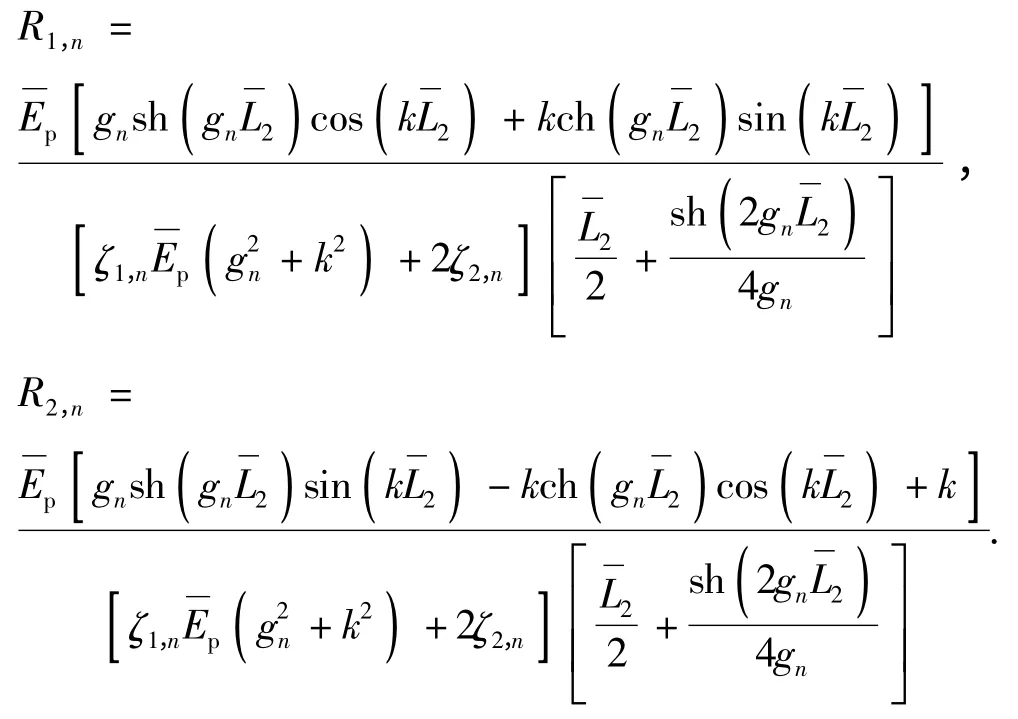
则埋入段桩身竖向位移幅值为

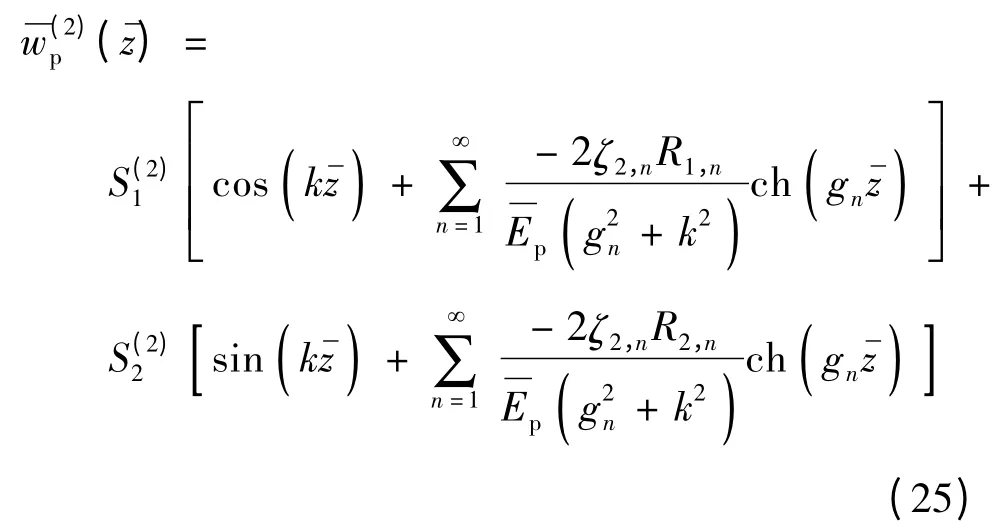
桩身任意一点的正应力可表示为

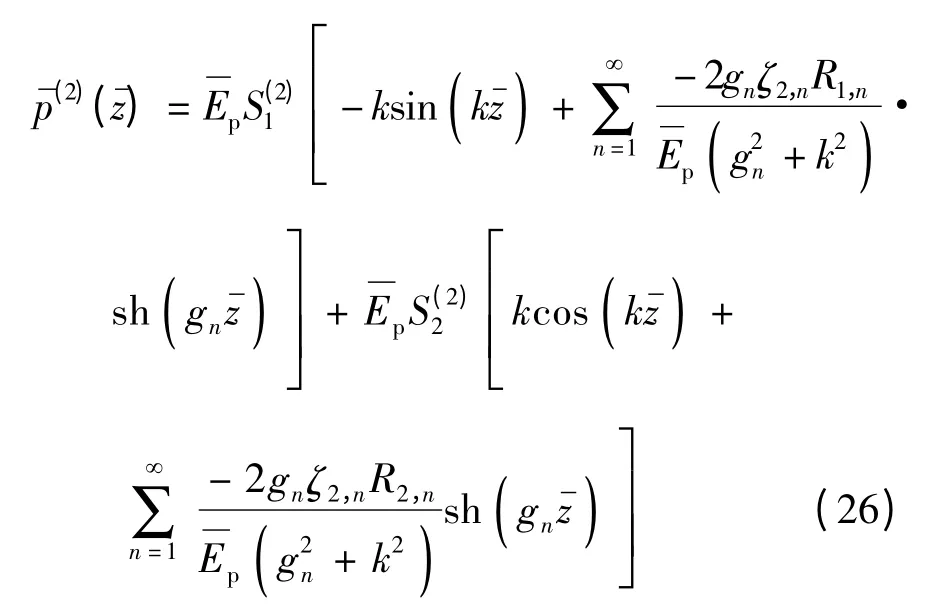
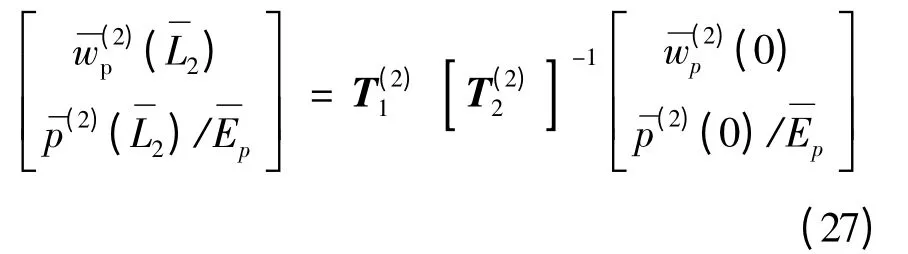
式中，T(2)1为2 ×2 的系数矩阵，各元素分别为

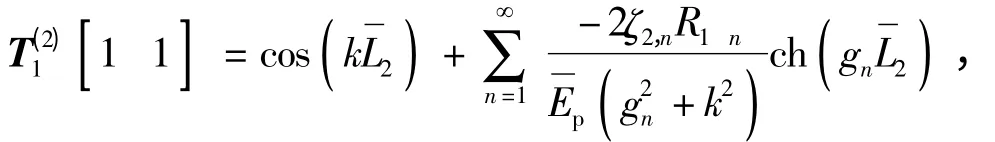
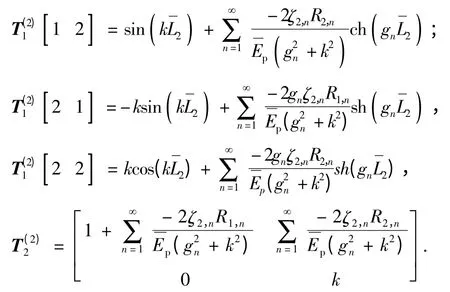
在自由段和埋入段分界处(z =0)，桩身位移和应力满足连续性条件，即

对于桩顶作用简谐荷载P0eiωt，存在，同时将式(21)和(27)代入上式，可得

考虑桩端为弹性支承，令k*b= kb/ (μ r0)，则式(8)可写成如下无量纲形式:

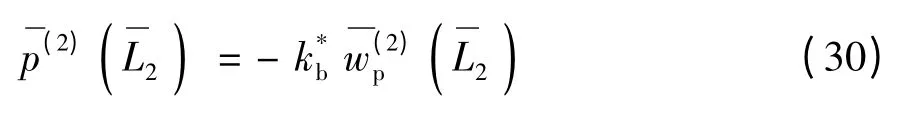
由式(29)和(30)可得部分埋入桩无量纲形式的桩顶阻抗为

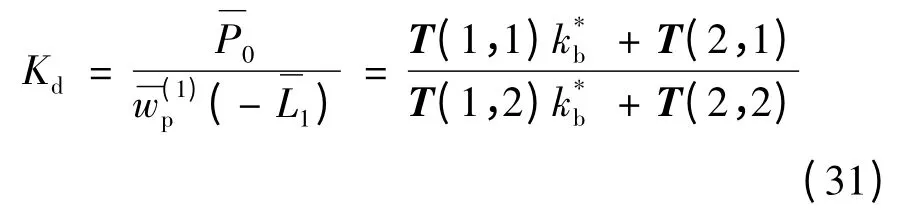
值得说明的是，当考虑土底和桩端土体阻尼效应时，只需将以上结果中的反力系数ks、kb分别用ks+iωηs、kb+iωηb代替即可，形成复刚度，其余不作改变，其中ηs、ηb分别代表土层底部和桩端地基的阻尼系数.

3 计算与讨论

为验证上述理论推导的正确性，并考虑到目前尚无严格非饱和条件下桩的解析和试验结果，令Sr=0.9999、As=0、L1=0，将文中解退化到以往饱和状态下的全埋入桩情况，与文献［17］的结果进行对比.原文仅列出了各参数的无量纲形式，换算成实际参数分别为:土层，Ks= 22.5 GPa、ρs= 2 712.3 kg/m3、Kb=675 MPa、μ =311.5 MPa、n =0.482、κ =6.52 ×10-13m2;基桩，Ep=809.9 GPa、ρp=2 264.2 kg/m3;土层底部地基反力系数为k*s =0.01.由图2(a)可知，按三相介质动力方程得出的桩顶复动刚度无论实部(Re)还是虚部(Im)都与Zeng 等［17］的结果基本一致(图中变量含义同文献［17］).此外，张玉红等［18］应用间接边界元法对饱和土与桩基础动力相互作用进行了分析，文中解在变化规律上与其结果大致相同(见图2(b)).数值差异可能来自于模型将底部土层简化为弹簧支承的假定及弹簧刚度取值上.鉴于目前尚无商业软件能够精确模拟非饱和土动力特性，且严格考虑桩端土体真三维波动效应及桩土耦合作用将显著增加理论求解的难度，文中按Winkler 地基模式处理桩端支承不失为一种简便可行的办法.

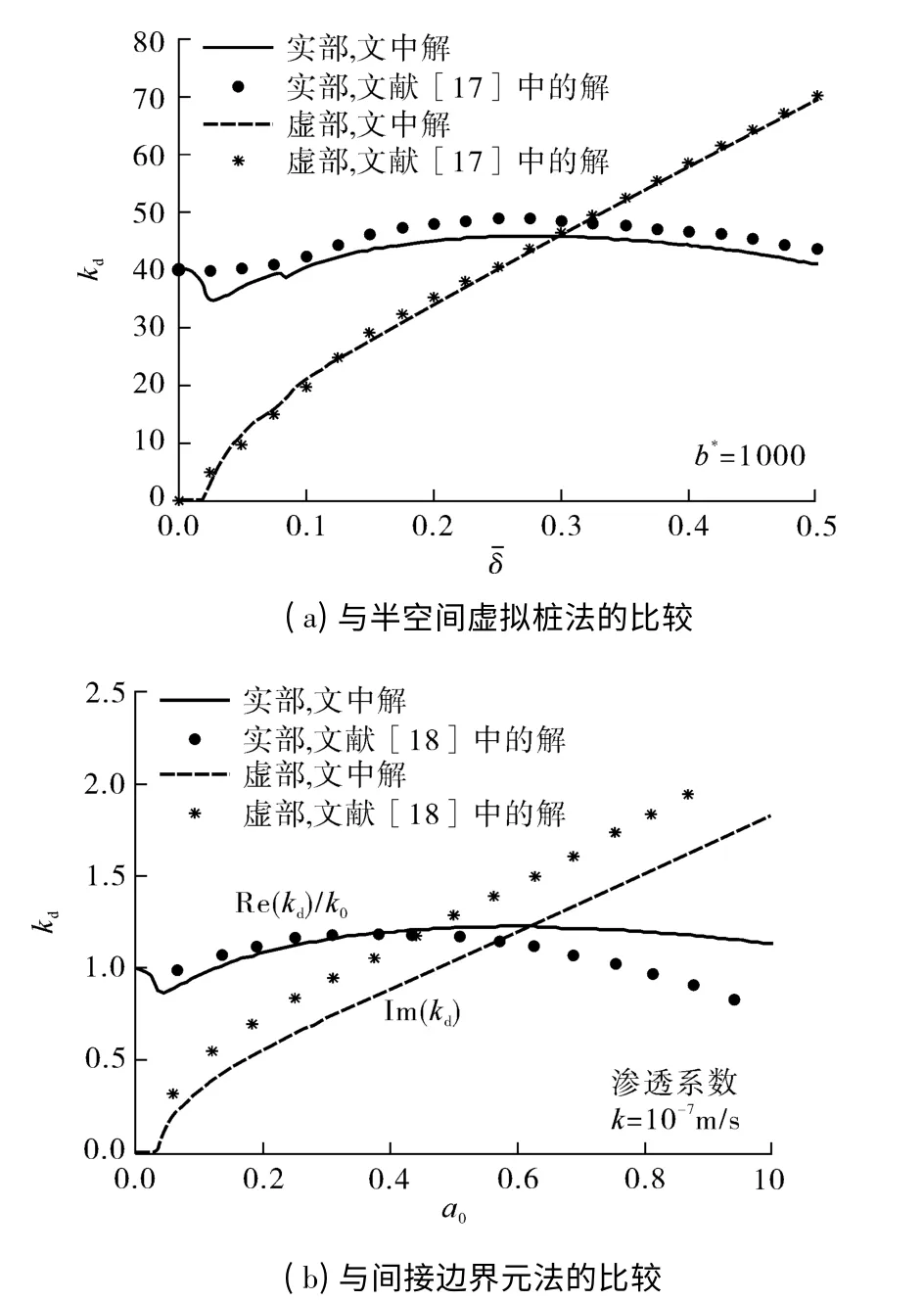
图2 饱和两相介质解与其他解的对比Fig.2 Contrast with the solutions of two-phase saturated medium

为讨论不同参数对部分埋入桩竖向动力阻抗的影响，选取如下计算参数:土颗粒，Ks=36 GPa，ρs=2700 kg/m3;水，Kf=2.0 GPa，ρf=1 000 kg/m3，ηf=1.0×10-3Pa·s;空气，Ka=145 kPa，ρa=1.29 kg/m3，ηa=18×10-6Pa·s;土骨架，Kb=698MPa，μ=72.2MPa，n=0.45，γ=Sr，Sw0=0.05，κ=1.0×10-8m2、ks*=1.0;V-G 模型拟合参数，χ =1.0 ×10-4Pa-1，m=0.5，d =2;基桩，Ep=36.1 GPa，ρp=2500 kg/m3、L2=20m.图中横坐标采用无量纲频率，其中d为桩径.

埋入段桩长保持不变时，桩身自由段长度L1对桩顶阻抗的影响如图3所示.

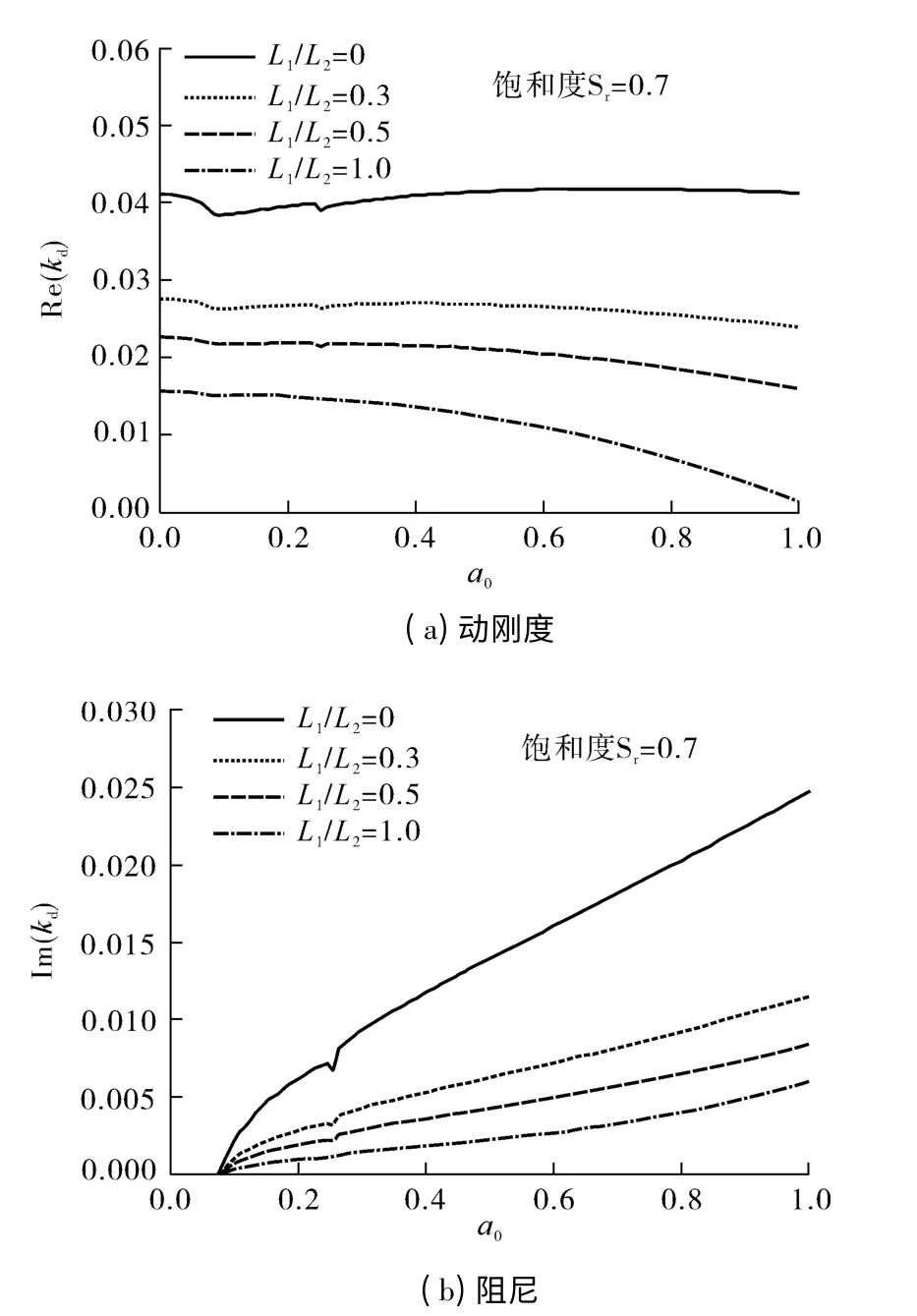
图3 埋入比对桩顶阻抗的影响Fig.3 Effect of length ratio on the vertical impedance of piles

由图3可知，桩身外伸部分的存在增大了桩基础的柔性，使桩顶动刚度和阻尼大幅度降低.当埋入比L1/L2=1.0、无量纲频率a0=1.0 时，动刚度降至0左右，阻尼降低幅度接近80%，且动刚度随频率的增大而逐步降低，阻尼间的差异也逐渐增大.为保证结构安全性，工程设计中应格外重视埋入比的合理取值.然而，阻尼曲线的第一共振频率则基本不受自由段桩长的影响，原因在于该共振是由有限厚度土层中横波的传播与反射引起的，主要受土层条件控制.

频率10、20 和30 Hz 时桩顶动刚度和阻尼随饱和度的变化曲线如图4所示.

由图4可知，动刚度随饱和度的升高而缓慢增大，达到峰值后缓慢减小，其中高频振动时较为明显，而阻尼则基本不随饱和度变化.这是由于频率较高时孔隙流体的惯性耦合作用较为强烈，对桩动力特性的影响也更为显著，低频振动时的惯性效应则较弱.但总的说来，阻抗曲线变化幅度不大，饱和度本身对桩竖向振动特性的影响较为有限.需要说明的是，由于非饱和土中存在毛细压力现象，产生的基质吸力使土体颗粒间有效应力增加，从而提高了土的的抗剪强度，继而使动剪切模量增大，并最终影响埋置结构的动力响应.由于本研究旨在探讨Sr本身对单桩动力特性的影响，故此处对饱和度的这种间接作用不作进一步讨论，相关内容可参考文献［16］.

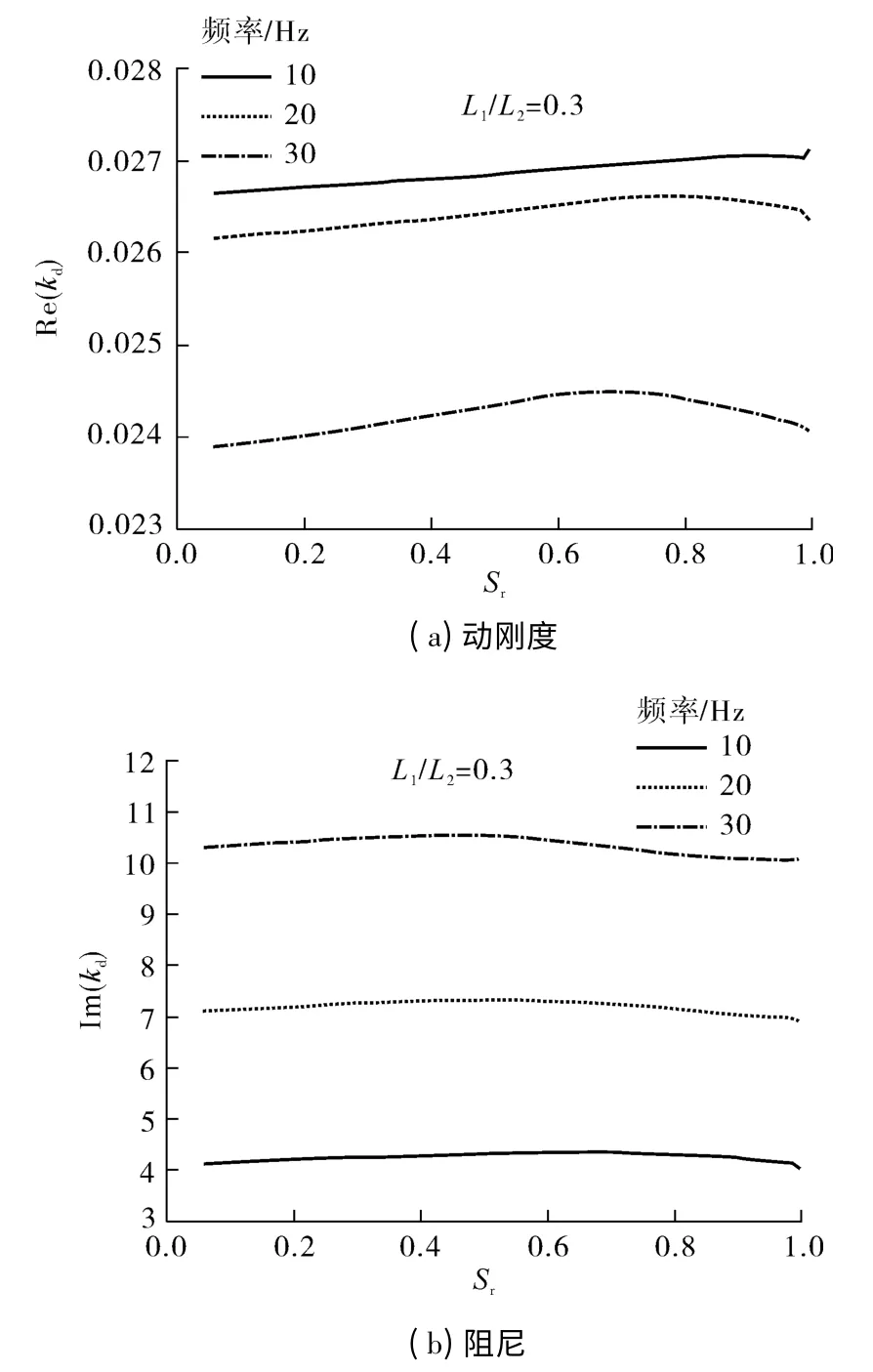
图4 土体饱和度对桩顶阻抗的影响Fig.4 Effect of saturation on the vertical impedance of piles

基桩在稳态振动下，桩周附近将产生向外辐射的柱状波，从而引起自由场的动力响应.桩顶作用单位荷载幅值=1，不同饱和度下地表位移幅值沿径向的分布曲线如图5所示.

由图5可知，随距离的增加，位移uz呈指数衰减趋势，且不同饱和度下的差异逐渐增大.当距基桩中心10r0时，位移大小降至桩侧位置的20% ～30%.在群桩基础桩-桩动力相互作用的分析中，该位移近似为相邻桩振动引起的附加位移.

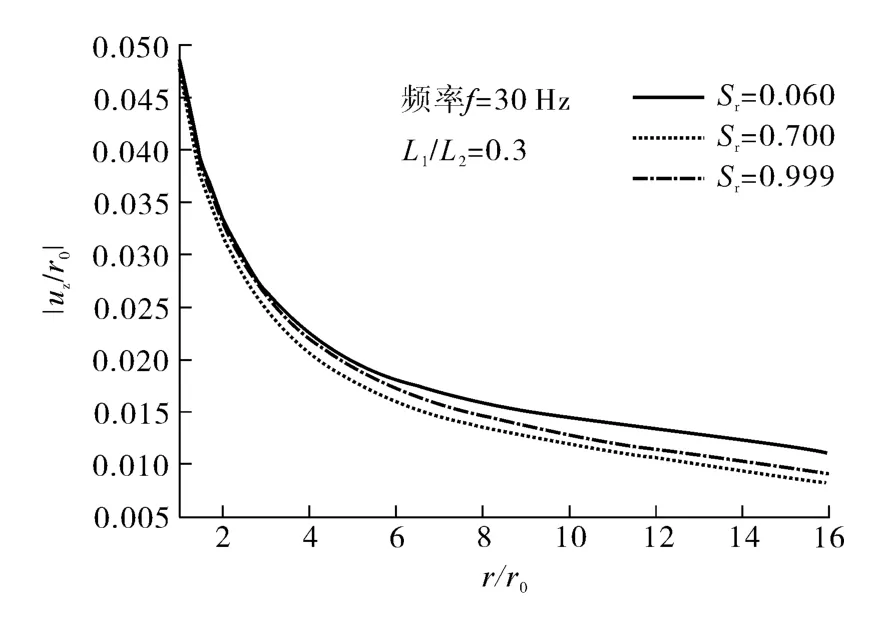
图5 地表位移幅值随距离的变化Fig.5 Variation of surface displacement amplitude with distance

地表6r0处地表位移幅值随频率的变化规律如图6所示.为表达方便，图中纵坐标采用ωuz表示，由于与桩顶速度导纳iω/kd的定义类似，这里称之为地表点的速度导纳.

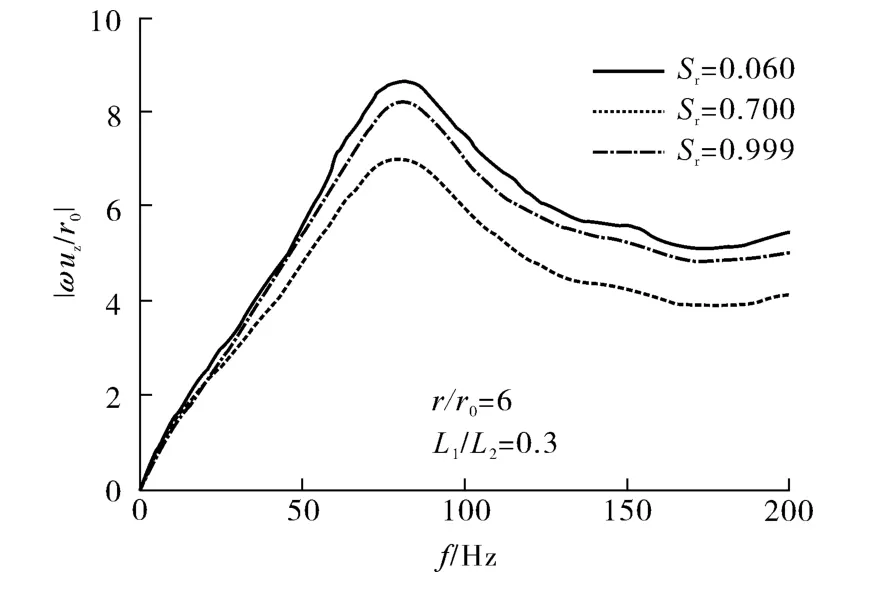
图6 r/r0 =6 处地表位移幅值随频率的变化Fig.6 Variation of surface displacement amplitude with frequency(r/r0 =6)

由图6可知，随着频率的增大，导纳值逐渐增大，并在80 Hz 左右达到峰值;此后，不同饱和度下的速度导纳差值基本相同，且Sr=0.7 时速度导纳值最小.由于导纳和复刚度存在简单的倒数关系，不难看出，这与图4中复刚度在饱和度0.7 附近达到最大值的规律相一致.

Sr=0.7、L1/L2=0.3 时土层底部不同地基反力系数对桩顶阻抗的影响如图7所示.

由图7可知，地基反力系数的影响主要体现在低频阶段，地基反力系数较小时，即土层底部较软，横波共振频率(对应第一个共振点)相应较低，表明横波剪切共振的消弱作用较低.该共振点在阻尼曲线上表现为一截止频率，低于该频率，土层阻尼很小.随着频率的进一步增大，不同地基反力系数下的刚度和阻尼值则基本保持相同.

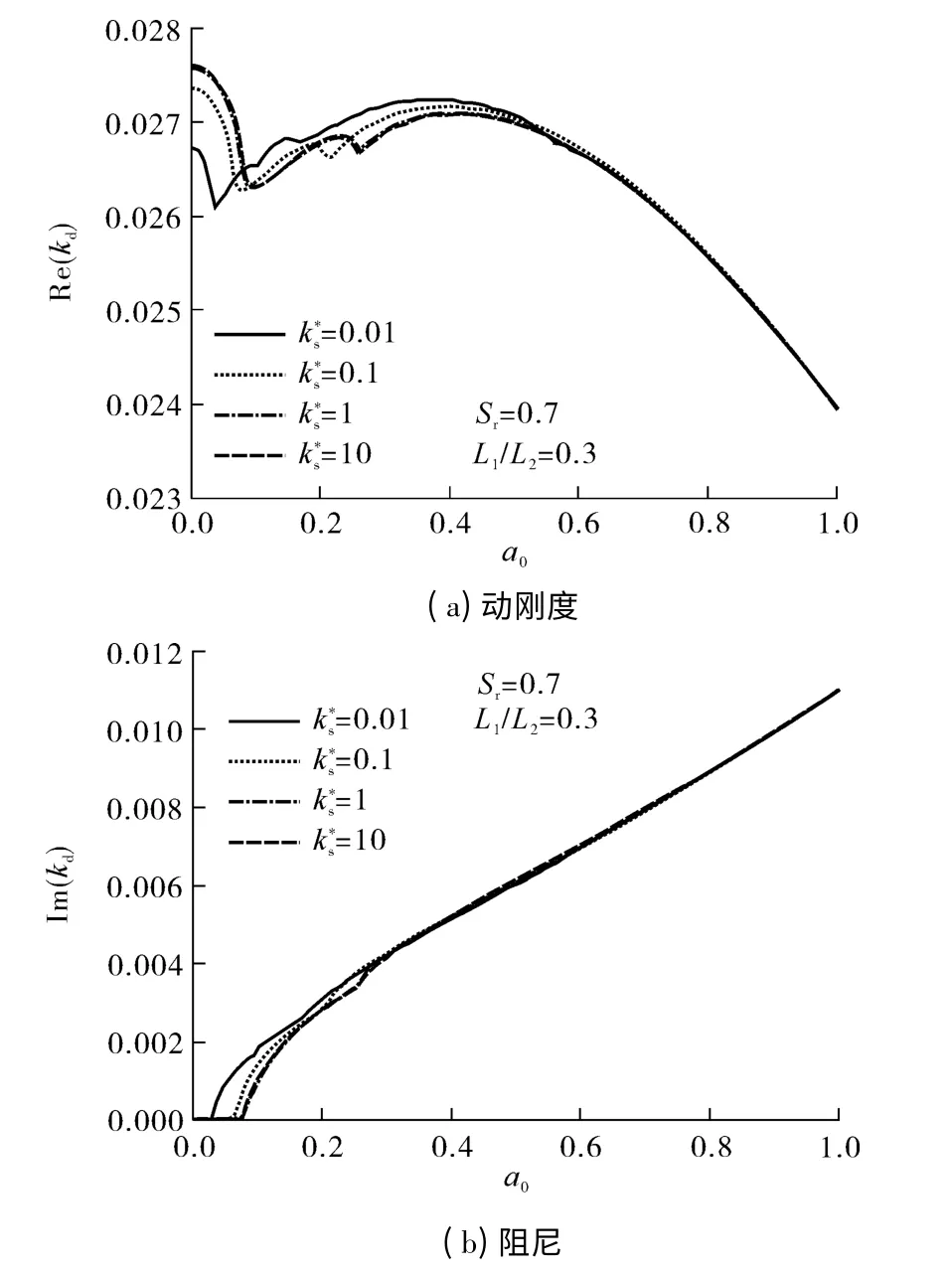
图7 土底反力系数对桩顶阻抗的影响Fig.7 Effect of reaction coefficient at soil layer bottom on the vertical impedance of piles

饱和度Sr分别为0.7 和0.999 时，渗透系数对桩顶阻抗的影响如图8所示.图中κ 为土体固有渗透系数，转换为常用的Darcy 渗透系数分别为10-1、10-3和10-5m/s.

由图8可知，当土体处于非饱和状态时，3 种渗透系数下的计算曲线差别很小，此时孔隙水的流动性对桩的动力响应几乎不产生作用.土层接近完全饱和时，渗透系数的影响才逐渐体现，表现为土体渗透性降低，阻抗增大，特别是在高频阶段，尤为明显.这表明孔隙水对桩动力特性的参与作用只在准饱和或完全饱和状态时才得以发挥.

为研究桩竖向振动所引起的土层振动特性，引入无量纲土层复阻抗因子γs=ζ2，n/ζ1，n，其实部和虚部分别代表土层动力反应的刚度和阻尼部分.土层的阻抗作用由无数个单独模态组合叠加而成(对应n=1，2，3，…)，但一般说来，仅前几阶模态具有明显的表征特性.不同土底反力系数对1 -3 阶土层阻抗因子的影响如图9所示.

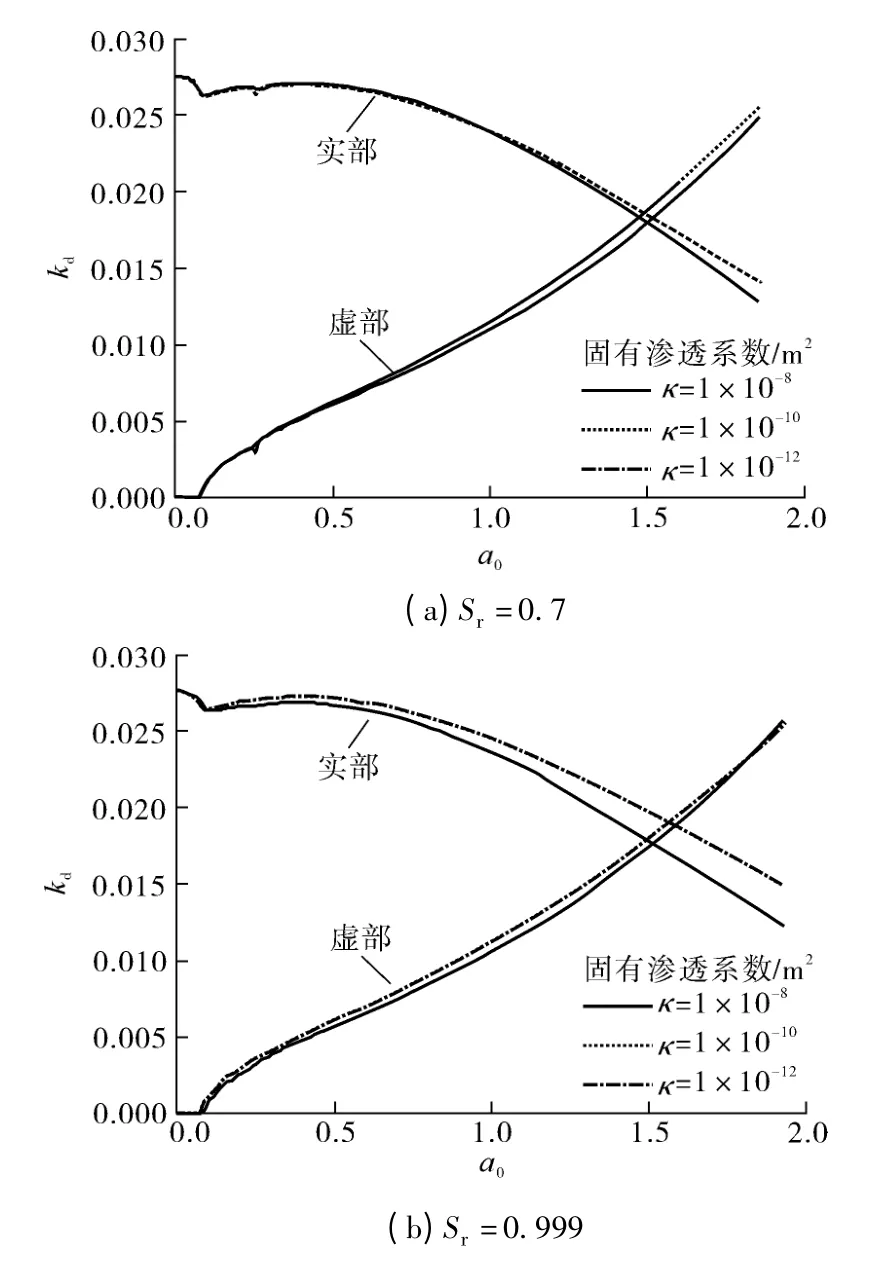
图8 土体渗透系数对桩顶阻抗的影响Fig.8 Effect of permeability on the vertical impedance of piles

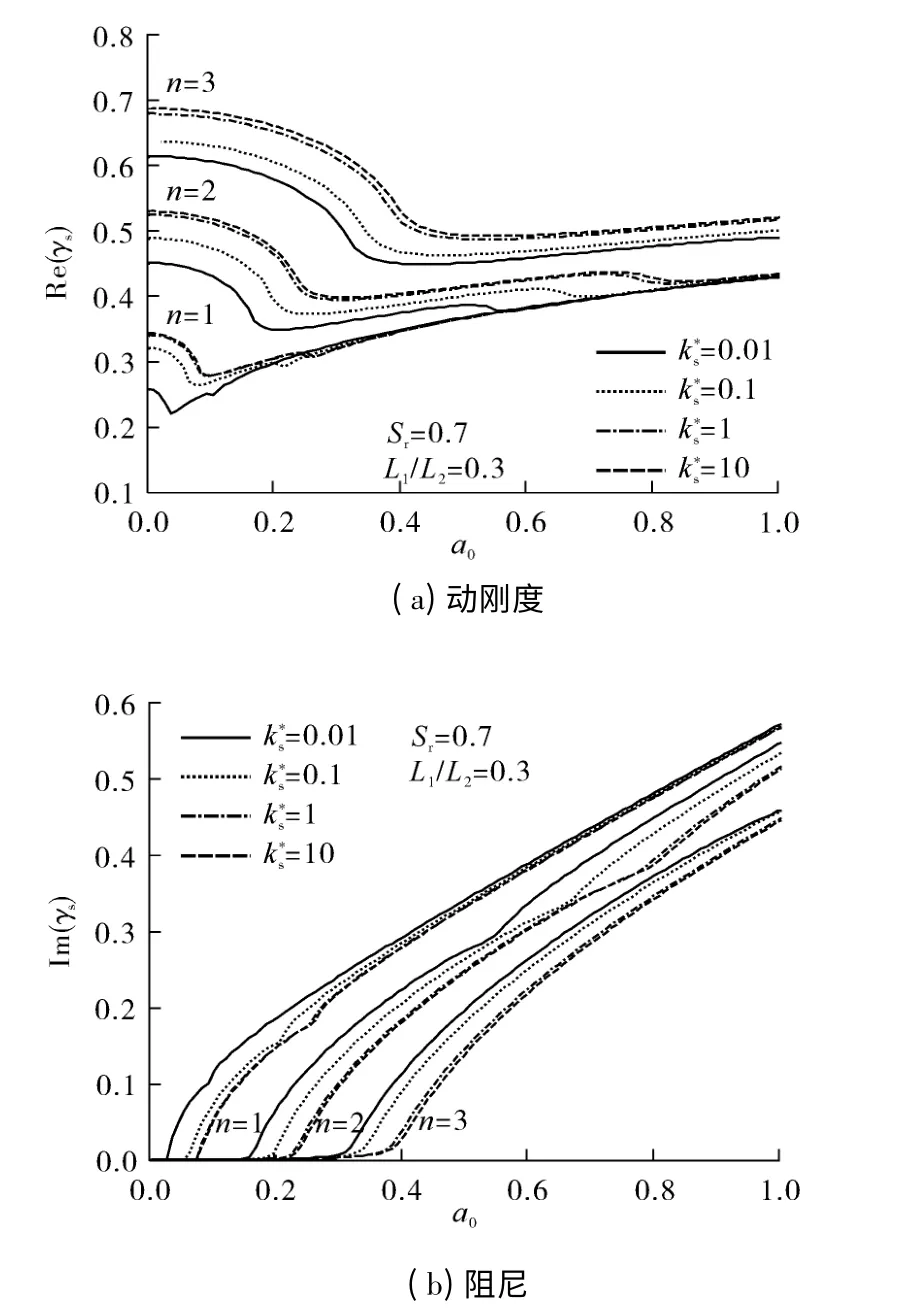
图9 土底反力系数对土层阻抗因子的影响Fig.9 Effect of reaction coefficient at soil layer bottom on the resistance factor of soil layer

由图9可知:土底反力系数对土层阻抗存在显著影响.土层阻抗刚度部分随着k*s的增加而增加，刚度最小处所对应的共振频率(对应阻尼曲线的截止频率)也相应增加，而阻尼部分则随之降低;且随着频率的增大，同一模态下阻抗因子间的差异逐渐减小.从土层复阻抗因子的表达式可以看出，γs是一个与土层和荷载特性密切相关的量，其变化受土层剪切模量、厚度、泊松比、模态阶数和激振频率等参数的影响，而与基桩特性关系不大.

4 结论

针对非饱和土中部分埋入式弹性支承桩的竖向振动问题，采用三相多孔介质波动方程，考虑不同相之间的耦合效应和毛细压力作用，借助算子分解和分离变量法，并结合桩端弹性支承假定，导出了简谐振动下部分埋入桩阻抗函数的封闭解，计算结果表明:

(1)桩顶复刚度随自由段桩长的增加而大幅降低，阻尼曲线的第一共振频率则基本不受此影响;

(2)频率较高时，随着土体饱和度的升高，动刚度缓慢增大，达到峰值后则缓慢减小，阻尼则基本保持不变，总的说来，在桩竖向振动特性的影响因素中，饱和度的作用较为有限;

(4)土体处于非饱和状态时，不同渗透系数下的桩顶阻抗差别很小，孔隙水对桩基动力特性的参与作用只在准饱和或完全饱和时才得以发挥.

［1］Lee B K，Jeong J S，Fan L G，et al.Free vibrations of tapered piles embedded partially in Winkler type foundations ［J］.KSCE Journal of Civil Engineering，1999，3(2):195-203.

［2］Catal H H.Free vibration of partially supported piles with the effects of bending moment，axial and shear force［J］.Computers Structures，2002，24(12):1615-1622.

［3］Catal H H.Free vibration of semi-rigid connected and partially embedded piles with the effects of the bending moment，axial and shear force ［J］.Engineering Structures，2006，28(14):1911-1918.

［4］Yusuf Y，Hikmet H C.Free vibration of piles embedded in soil having different modulus of subgrade reaction ［J］.Applied Mathematical Modelling，2008，32(5):889-900.

［5］Sapountzakis E J，Kampitsis A E.Nonlinear dynamic analysis of Timoshenko beam-columns partially supported on tensionless Winkler foundation ［J］.Computers and structures，2010，88(21):1206-1219.

［6］任青，黄茂松，钟锐，等.部分埋入群桩的竖向振动特性［J］.岩土工程学报，2009，31(9):1384-1390.Ren Qing，Huang Mao-song，Zhong Rui，et al.Vertical vibration of partially embedded pile groups［J］.Chinese Journal of Geotechnical Engineering，2009，31(9):1384-1390.

［7］任青，黄茂松.分层地基中柔性高承台群桩基础的竖向振动特性［J］.土木工程学报，2009，42(4):107-113.Ren Qing，Huang Mao-song.Analysis of axial vibration of floating pile groups with flexible caps in layered soils［J］.China Civil Engineering Journal，2009，42(4):107-113.

［8］钟锐，黄茂松，任青，等.考虑土体非线性的部分埋入群桩竖向振动分析［J］.同济大学学报:自然科学版，2011，39(12):1360-1366.Zhong Rui，Huang Mao-song，Ren Qing，et al.Analysis of dynamic response of partially embedded pile group with a consideration of soil nonlinearities in vertical vibration［J］.Journal of Tongji University:Natural Science，2011，39(12):1360-1366.

［9］余云燕，余莉芬.均质土中部分埋入变模量桩的波动响应研究［J］.振动工程学报，2010，23(2):200-205.Yu Yun-yan，Yu Li-fen.Transient wave of the pile with variable modulus embedded partially in homogeneous soil［J］.Journal of Vibration Engineering，2010，23(2):200-205.

［10］张智卿，王奎华，谢康和，等.成层非饱和土中桩的纵向振动特性分析［J］.科技通报，2007，23(1):88-96.Zhang Zhi-qing，Wang Kui-hua，Xie Kang-he，et al.A study on longitudinal vibration behavior of inhomogeneous pile embedded in layered unsaturated soils［J］.Bulletin of Science And Technology，2007，23(1):88-96.

［11］张智卿，王奎华，李强，等.非饱和土中端承桩纵向振动问题简化解［J］.工程力学，2010，27(5):159-165.Zhang Zhi-qing，Wang Kui-hua，Li Qiang，et al.Simplifiedsolution for vertical vibration of an end bearing pile embedded in unsaturated soil ［J］.Engineering Mechanics，2010，27(5):159-165.

［12］徐明江.非饱和土地基与基础的动力响应研究［D］.广州:华南理工大学土木与交通学院，2010.

［13］Lysmer J，Richart F E.Dynamic response of footing to vertical load［J］.Journal of Soil Mechanics and Foundation Division，ASCE，1966，92(SM1):65-91.

［14］陈龙珠，陈胜立.饱和地基上刚性基础的竖向振动分析［J］.岩土工程学报，1999，21(4):392-397.Chen Long-zhu，Chen Sheng-li.Vertical vibration of a rigid circular footing on saturated soil［J］.Chinese Journal of Geotechnical Engineering，1999，21(4):392-397.

［15］Zhang M，Wang X H，Yang G C，et al.Solution of dynamic Green's function for unsaturated soil under internal excitation［J］.Soil Dynamics and Earthquake Engineering，2014，64:63-84.

［16］王星华，章敏.非饱和土半空间中单桩竖向振动特性研究［J］.岩土工程学报，2013:35(7):1210-1220.Wang Xing-hua，Zhang Min.Dynamical response of vertically loaded pile in half-space of unsaturated porous media［J］.Chinese Journal of Geotechnical Engineering，2013:35(7):1210-1220.

［17］Zeng X，Rajapakse R K N D.Dynamic axial load transfer from elastic bar to poroelastic medium ［J］.Journal of Mechanical Engineering，1999，125(9):1048-1055.

［18］张玉红，黄义.流体渗透系数对饱和土中桩基础阻抗函数的影响［J］.西安交通大学学报，2001，35(4):407-410.Zhang Yu-hong，Huang Yi.Effect of permeability coefficient of two-phase saturated soils on impedance functions of piles［J］.Journal of Xi'an Jiaotong University，2001，35(4):407-410.