波形钢腹板梁桥腹板抗剪强度特性分析

赵磊，王涛，张兴，王芳

（1.贵州大学土木工程学院，贵州贵阳 550025；2.贵州大学机械工程学院，贵州贵阳 550025）

波形钢腹板梁桥腹板抗剪强度特性分析

赵磊1，王涛1，张兴1，王芳2

（1.贵州大学土木工程学院，贵州贵阳 550025；2.贵州大学机械工程学院，贵州贵阳 550025）

基于理论计算与ABAQUS有限元软件，对波形钢腹板简支梁桥腹板截面的不同弯折角度及弯折段与直线段不同长度模型进行计算，分析了波形钢腹板梁桥腹板抗剪强度特性。结果表明，在外部荷载作用下，随着腹板弯折角度的增大，腹板所受剪应力逐渐增大；大角度腹板可有效提高波形钢腹板承担竖向剪力的比例，使砼梁板受到的剪应力减小；在腹板弯折角一定的情况下，与腹板的弯折段和直线段采用等长截面形式相比，采用不等长截面形式所受剪应力较大；与波形钢腹板相比，直腹板梁桥受力较差。

桥梁；波形钢腹板；抗剪强度；剪应力；截面形式

波形钢腹板与砼腹板最主要的不同在于波形钢腹板几乎承受主梁上的全部剪力，且剪应力大小沿梁高度方向近似相等。在相关设计中，波形钢腹板的几何尺寸由其抗剪强度决定，即钢腹板上的应力应小于所选钢材的设计抗剪强度。中国对波形钢腹板箱梁的引进较晚，目前对它的研究处于初级阶段，也只修建了为数不多的波形钢腹板箱梁桥，其中河南卫河大桥是国内第一座将波形钢腹板梁桥应用于高速公路的简支桥梁。该文以该桥中跨跨度52 m简支段作为模拟原型，取钢腹板厚度t为10 mm，采用ABAQUS有限元数值模拟方法计算波形钢腹板的应力，然后改变波形钢腹板的主要几何参数尺寸，研究各几何参数对波形钢腹板受力性能的影响，为波形钢腹板梁桥腹板设计提供参考。

1 工程背景

河南卫河大桥采用简支三跨结构，跨径组合为47 m+52 m+47 m。横断面采用单箱三室直腹式等截面箱梁，梁高3.2 m，主跨高跨比为1／16.25。顶板宽16.85 m，底板宽11.85 m，翼缘板悬长2.5 m，顶板厚25 cm，顶板端部厚20 cm，底板厚22 cm（见图1）。

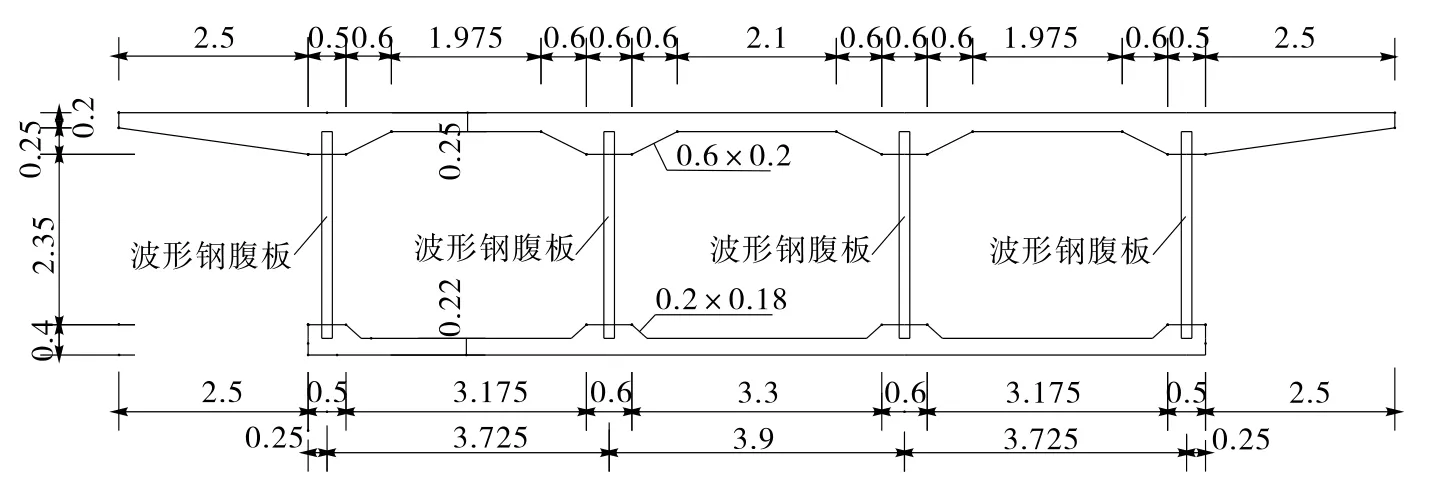
图1 河南卫河大桥上部结构断面图（单位：m）

以其中跨跨度52 m简支段为模拟原型，取箱梁顶底板砼为C50，波形钢腹板采用Q345型钢，设计抗拉、抗压、抗弯应力f 为310 MPa，抗剪强度fv为180 MPa，设计采用公路-Ⅰ级荷载。波形钢腹板主要几何参数（见图2）如下：一个周期波形钢腹板的水平总长度l=1 600 mm；波形钢腹板的直板段水平长度a=430mm；斜板段水平长度c= 370 mm；波高h=220 mm；水平折叠角β=30.7°；板厚t=10 mm；腹板高度hw=2.73 m。

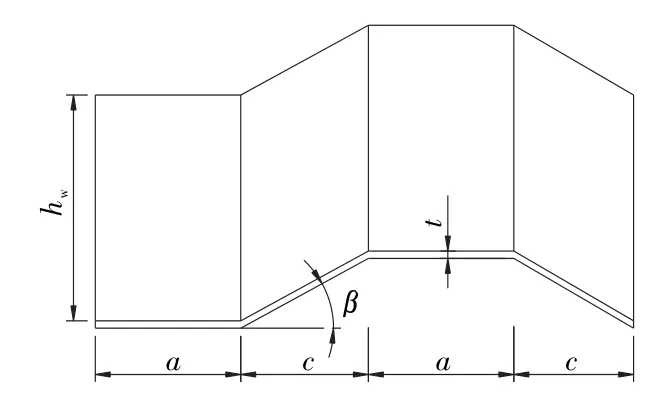
图2 波形钢腹板几何参数示意图

2 计算理论

波形钢腹板梁桥腹板的受力以剪力为主，整座桥梁的剪力主要由腹板承担，假定其剪力全部由腹板承担。依据JTG D60-2015《公路桥涵通用设计规范》计算剪力效应，公路-Ⅰ级荷载集中力pk= 1.2×360 k N=432 k N，均布荷载qk=10.5 k N／m，荷载布置见图3。由于腹板主要承担剪力，几乎不承担弯矩作用，故取桥纵向剪力最大值的支点附近为计算截面，剪力影响线见图4。

图3 波形钢腹板几何参数

图4 支点附近剪力影响线

由于ABAQUS中已考虑结构自重作用效应，在依据规范计算支点剪力效应过程中只需计算可变作用作为基本组合效应的设计值Sud，取安全等级为二级，且采用车道荷载计算，则结构重要性系数γ0=1，γQ1=1.4。对于52 m简支梁桥，根据影响线布置荷载得：假定剪力全部由波形钢腹板承担，考虑支点横隔板整面约束作用效应，支点的各片梁组成的整体截面剪应力强度近似采用基本公式计算：

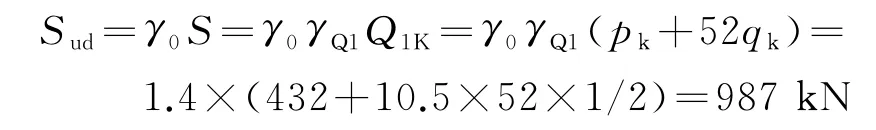
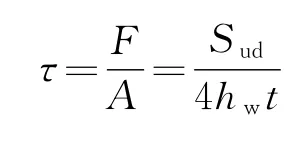
3 腹板不同弯折角度模型计算分析

3.1 腹板弯折角度30.7°

取腹板水平折叠角β=30.7°，板厚t=10 mm，腹板高度hw=2.73 m（见图5）。采用Solid三维实体单元建立模型，单元计算网格采用C3D8R三维六面体二次减缩元。砼弹性模量为34.5 GPa，泊松比为0.2；型钢弹性模量为206 GPa，泊松比为0.3。边界采用铰支约束，采用公路-Ⅰ级荷载加载。模型计算结果见图6。在ABAQUS有限元软件中，坐标轴1、2、3方向分别代表坐标x、y、z轴，剪应力τ= τyz即为桥梁横截面向上或向下方向的剪应力S23。

图5 腹板弯折角度为30.7°单周期截面尺寸（单位：mm）

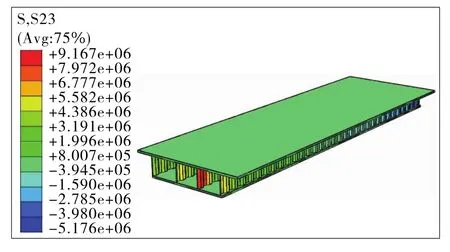
图6 腹板弯折角度30.7°有限元模型计算结果（单位：Pa）

腹板厚度t=10 mm时，理论抗剪强度为：

根据图6，τmax=S23max=9.17MPa，与理论计算值基本吻合。

3.2 腹板弯折角度60°

腹板弯折角度取60°进行模型分析计算，腹板截面见图7，其中砼顶、底板及尺寸、腹板厚、高度、材料强度等材料条件同3.1节。计算结果见图8。

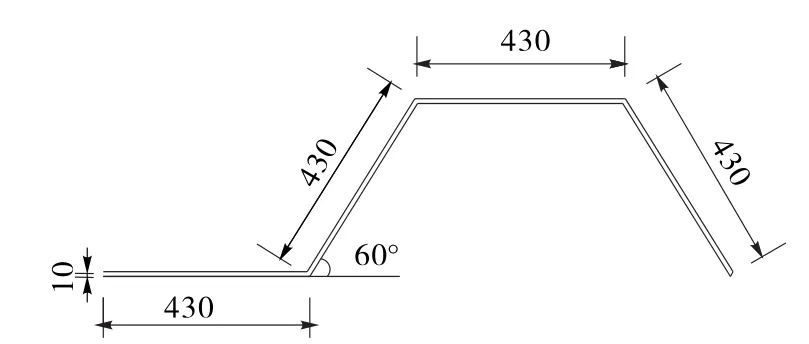
图7 腹板弯折角度60°单周期截面尺寸（单位：mm）

图8 腹板弯折角度60°有限元模型计算结果（单位：Pa）

根据图8，τmax=S23max=12.22MPa。与弯折角

度30.7°的波形钢腹板梁桥相比，60°弯折角度的波形钢腹板承担了更大部分竖向剪力，与前者相比，60°弯折角度腹板的砼顶、底板所受到的竖向剪力显著减小。

3.3 腹板弯折角度0°（直板）

腹板弯折角度取0°进行模型分析计算，腹板截面直接由波形变换为平直钢板，厚度取10 mm；砼顶、底板及尺寸、腹板高度、材料强度等材料条件同3.1节。计算结果见图9。

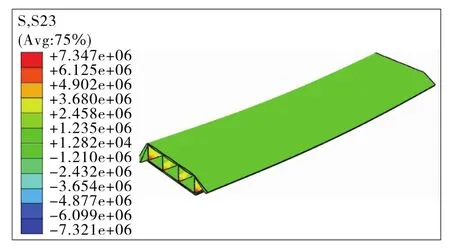
图9 腹板弯折角度0°时有限元模型计算结果（单位：Pa）

根据图9，τmax=S23max=7.35MPa，说明0°弯折角度的腹板只承担了小部分竖向剪力，且桥梁发生了整体屈曲，虽然腹板剪应力较小，但受力情况极差。

3.4 不同弯折角度模型计算结果分析

波形钢腹板梁桥腹板不同弯折角度模型计算结果见表1。

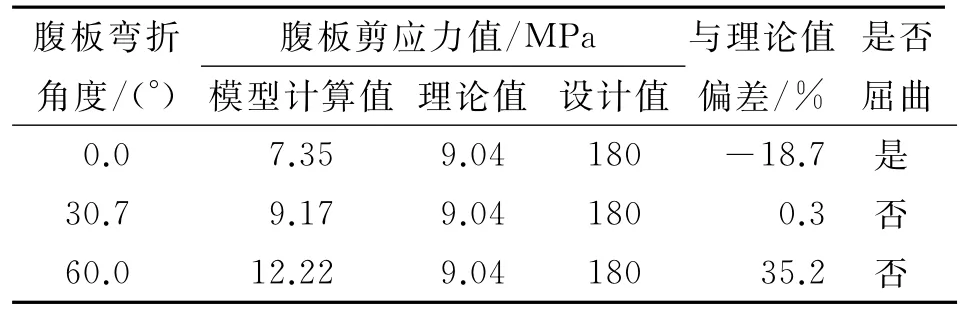
表1 腹板剪应力与弯折角度

从表1可以看出：在外部荷载作用下，随着腹板弯折角度的增大，腹板所受剪应力逐渐增大，其函数关系近似为线性关系；30.7°弯折角度腹板的受力较接近理论计算结果；60°弯折角度腹板承担的竖向剪力相对较多，使砼分担的剪力显著减小，证明大角度腹板能提高波形钢腹板分担竖向剪力的比例，使砼承担更小的剪力；直腹板梁桥在型钢材料远未达到设计抗剪强度时即发生屈曲破坏，与波形钢腹板相比，直腹板梁桥受力较差。为了使波形钢腹板在屈曲之前更能发挥抗剪强度，可以考虑设计适中的腹板弯折角度。

4 弯折段和直线段不同长度模型计算分析

4.1 折减弯折段长度模型计算

对波形钢腹板梁桥1 600 mm型腹板弯折部分进行长度折减，取原长度的一半即215 mm作为弯折段长度进行模型计算，材料、尺寸、角度等其他指标同3.1节。腹板截面见图10，计算结果见图11。

图10 斜腹板为215 mm单周期截面尺寸（单位：mm）

图11 斜腹板为215 mm有限元模型计算结果（单位：Pa）

根据图11，τmax=S23max=10.72MPa。与斜腹板为430 mm波形腹板相比，215 mm斜腹板波形腹板承担了更大的竖向剪力，与前者相比，215 mm长斜腹板波形腹板受到的剪应力较大，受力情况较差，偏于危险。主要原因为减小腹板弯折段长度相当于减小腹板波高，使波形板的受力逐渐趋近于直板形式，其截面受力情况与直板极为相似，而且可以大胆推测，当腹板的波高逐渐减小时，腹板应力将逐渐增大，桥体将逐渐出现局部及整体屈曲，其受力趋近于直板截面屈曲形式。因此，在设计中不可使腹板相对波高过小，要特别注重波形钢腹板梁桥腹板弯折段长度或波高的计算及取值。

4.2 折减直线段长度模型计算

对3.1节中的腹板直线部分进行长度折减，取原长度的一半即215 mm作为直线段长度进行模型计算，材料、尺寸、角度等其他指标同3.1节。腹板截面见图12，计算结果见图13。

根据图13，τmax=S23max=9.91MPa，与斜腹板长度为215 mm的波形腹板相比，这种形式腹板应力偏小，但桥梁发生了整体和局部屈曲；与斜腹板长度为430 mm的波形腹板相比，这种形式腹板剪应

力相对较大，受力情况较差。为了不使波形钢腹板梁桥过早发生屈曲，在设计中不可使腹板相对波高过大，要特别注重波形钢腹板梁桥腹板直线段长度选取和计算。

前几天，我和几个同学聚会，十多年未见面了，大家都异常兴奋，在茶香氤氲的包间里，彼此亲切地询问着对方的近况。多年不见，昔日青涩懵懂的学友，如今都已成熟睿智，我们谈起了各自的生活，都想从别人那里寻找一些幸福感。

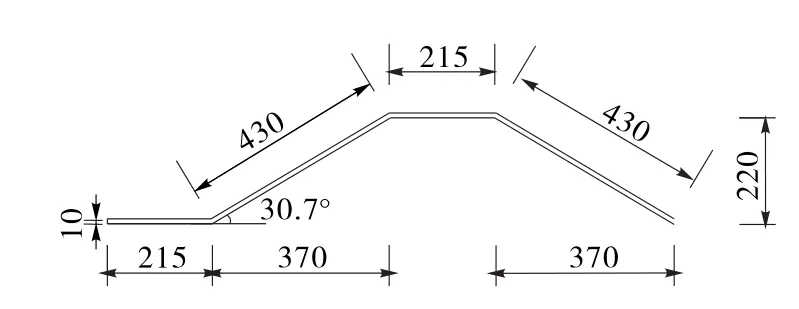
图12 直腹板为215 mm单周期截面尺寸（单位：mm）

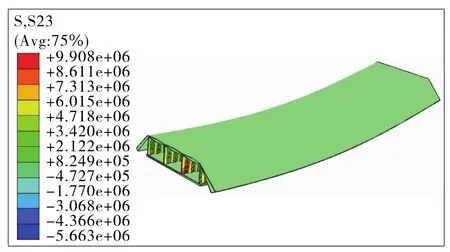
图13 直腹板为215 mm有限元模型计算结果（单位：Pa）

4.3 腹板截面单周期800 mm模型计算

取3.1节中波形钢腹板单周期长度1 600 mm的一半即800 mm，使腹板截面各部分长度均减到一半，并保持板厚度10 mm不变，以此作为波形钢腹板单周期长度进行模型计算，材料、尺寸、角度等其他指标同3.1节。腹板截面见图14，计算结果见图15。

根据图15，τmax=S23max=7.42MPa，相比于腹板单周期长1 600 mm各种类型受力情况，腹板单周期长800 mm波形钢腹板梁桥所受剪应力更小，顶、底板砼所受剪应力也更小，腹板受力情况更好，主要是因为腹板剪应力分布沿桥纵向更为均匀、合理。因此，要特别注重波形钢腹板梁桥腹板单周期长度的计算及取值。

图14800 mm单周期截面尺寸（单位：mm）

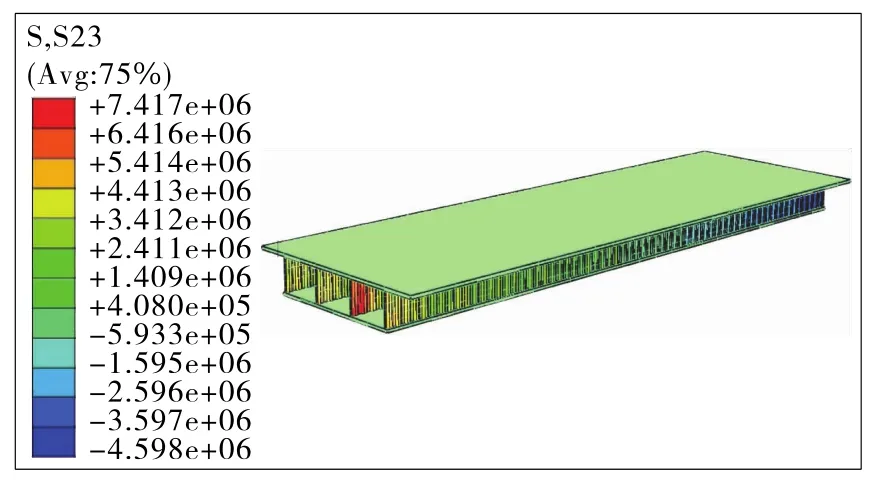
图15 腹板单周期800 mm有限元模型计算结果（单位：Pa）

4.4 弯折段和直线段不同长度模型结果分析

波形钢腹板梁桥腹板弯折段、直线段不同长度模型的计算结果见表2。

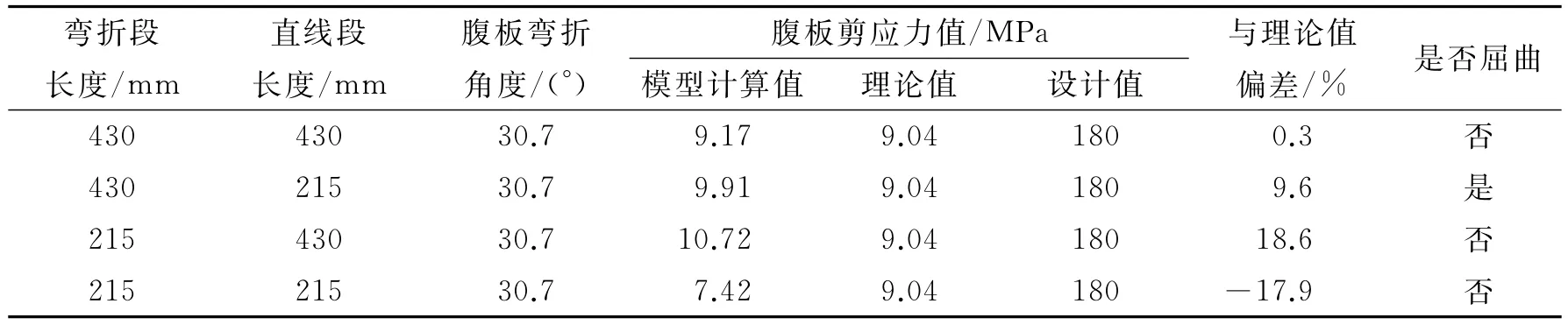
表2 腹板剪应力与弯折段、直线段长度

从表2可看出：在不改变腹板弯折角30.7°的情况下，当腹板弯折段、直线段长度采用不等长的截面模型时，腹板所受剪应力增大；弯折段、直线段长度均为430 mm的波形钢腹板所受剪应力最接近于理论计算值；弯折段、直线段长度均为215 mm的波形钢腹板所受剪应力最小。直线段与弯折段长度不相等的波形钢腹板在外荷载作用下受到的竖向剪应力比弯折段、直线段等长波形钢腹板更大，从而产生屈曲，承载能力不如弯折段、直线段等长的波形钢腹板。设计时应优先选用弯折段、直线段等长的结构形式，并重点计算和选用腹板单周期长度。

5 结论及建议

（1）在外部荷载作用下，随着腹板弯折角度的增大，腹板所受剪应力逐渐增大，其函数关系近似为线性关系。

（2）对于52 m波形钢腹板简支梁桥，采用单板周期1 600 mm，弯折角度30.7°，弯折段、直线段长度均为430 mm的波形钢腹板其受力较接近理论计算结果。

（3）60°弯折腹板承担的竖向剪力相对较大，砼顶、底板承担的剪力相对减小，证明大角度腹板能提高波形钢腹板承担竖向剪力的比例，使砼梁板受到的剪力减小。

（4）直腹板梁桥在型钢材料远未达到设计抗剪强度时即发生屈曲破坏，与波形钢腹板相比，直腹板梁桥受力较差，建议不采用0°直腹板形式。为了使波形钢腹板在屈曲之前更能发挥抗剪强度，可考虑设计适中的腹板弯折角度。

（5）在腹板弯折角为30.7°的情况下，当腹板弯折段、直线段长度采用不等长的截面模型时，腹板所受剪应力显著增大，且腹板斜边段相对较大的腹板截面形式受力较大，腹板直线段相对较短的腹板截面形式虽然受力较小但更容易发生屈曲。说明直线段与弯折段长度不等的波形钢腹板在外荷载作用下受到的竖向剪应力比弯折段、直线段等长波形钢腹板更大，较易屈曲，受力情况差。设计中建议不选用弯折段、直线段长度不等的波形钢腹板截面形式。

（6）弯折段、直线段长度均为215 mm的波形钢腹板所受剪应力最小，弯折段、直线段长度均为430 mm的波形钢腹板所受剪应力次之。设计时建议优先选用弯折段、直线段等长的结构形式，并根据工程特点重点计算和选用波形钢腹板单周期长度。

［1］ 陈宝春，黄卿维.波形钢腹板PC箱梁桥应用综述［J］.公路，2005（7）.

［2］ 朱越峰，吴朴，谢旭，等.部分波形钢腹板箱梁受力特性分析［J］.浙江大学学报：工学版，2008，42（1）.

［3］ GB 50017—2003，钢结构设计规范［S］.

［4］ JTG D60—2015，公路桥涵通用设计规范［S］.

［5］ JTG D62—2004，公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.

U448.21

A

1671-2668（2016）06-0165-05

2016-06-10