密闭圆筒仓内储粮自然对流及热湿耦合传递的研究
2015-12-19王远成白忠权张中涛
亓 伟 王远成,2 白忠权 张中涛
(山东建筑大学热能工程学院1,济南 250101)(可再生能源建筑利用技术教育部重点实验室2,济南 250101)
密闭圆筒仓内储粮自然对流及热湿耦合传递的研究
亓 伟1王远成1,2白忠权1张中涛1
(山东建筑大学热能工程学院1,济南 250101)(可再生能源建筑利用技术教育部重点实验室2,济南 250101)
粮食作为吸湿性多孔介质,具有吸湿和解吸湿特性。一般粮食收获后,大部分时间在密闭非通风状态下自然存储。鉴于粮仓外气候条件的季节和昼夜变化,会使粮堆的温湿度发生周期变化,导致超出存储安全指数。该文将以仓储粮堆内局部热湿耦合传递过程作为研究对象,借助多物理场数值模拟软件(COMSOL)进行数值模拟,研究近似冬夏季工况下粮堆内温湿度的动态变化规律,充分考虑了仓储粮作为吸湿性多孔介质具有复杂的热源、湿源。
吸湿性多孔介质 热湿耦合传递 多物理场数值模拟 圆筒仓储粮 自然对流
通常粮食收割后其水分含量比较大,对其干燥降低水分非常重要。粮食收获后,一般将其含水量降至12%~14%方可仓储,这样在一年的存储期内的大多数温度下粮食品质是安全的。谷物作为一种生物体,本身存在一定的呼吸作用,而且具有吸湿和解吸湿特性。对于粮堆子环境来说,其生物特征的变化必将影响周围存在的霉菌和昆虫等生物,这些对粮食的品质有一定损坏,谷物自身呼吸对其内部物质来说也有一定损耗。粮食干燥仓储后,在较长一段时间内处于非通风状态,粮堆内流体流动为自然对流。鉴于粮食温度及水分对粮食品质的影响,研究温度和水分对仓储粮堆内传热传质规律的影响有至关重要的作用。
该文对仓储粮热湿耦合传递规律进行了初步研究。研究主要考虑以下3点:1)研究的是粮堆在自然对流(非通风)条件下的热湿传递过程,而非强制对流(机械加压送风)条件下,机械加压送风粮食干燥过程前人已研究较多;2)研究充分考虑了粮食作为吸湿性多孔介质,本身具有吸湿和解吸湿特性,通过多物理场数值模拟软件(COMSOL)进行数学建模,将其特性以热源、湿源的方式添加到模型的源项之中;3)研究考虑到粮仓的非满仓存储,上部区域存有空气,所以将研究对象划分为双区域,即多孔介质区域和空气区域。通过模拟结果可以指导现实粮仓的温湿控制,阐明粮堆内粮食霉变、结霜发生机理,为提供解决和减轻粮食霉变、结霜措施提供理论依据,同时对研究粮堆内病虫群落分布规律有指导意义。
1 仓储粮堆内传热传质问题的研究现状
Fuji jian等[1]采用试验观测方法对加拿大北边地区的金属圆筒仓内小麦的温度和水分含量变化进行了一年时间的监测,逐时时间表明粮仓内小麦温度变化的峰谷值比外界温度变化的峰谷值延迟1个月,由于粮仓内温度梯度的影响,产生一定浮升力,引起粮仓内部空气的自然对流,最终导致其水分的迁移和再分配。Ruska Laszlo等[2]利用二维笛卡尔柱坐标系下的导热微分方程通过数值模拟得到了圆筒仓内粮堆温度随仓外气温变化的机理,但其研究忽略了粮食颗粒吸湿和解吸湿作用对相变潜热的影响以及颗粒表面水蒸汽的蒸汽阻力,并且未涉及水分迁移和再分配。Ali M.S.Al-Amri等[3]利用二维笛卡尔柱坐标系下的质扩散方程通过数值仿真得到了圆筒仓内粮堆水分迁移随仓外大气湿度变化的规律,此文献忽视了温度梯度对水分扩散的影响。K.K.Khankari等[4]利用数值模拟方法研究了在温度梯度影响下存储粮堆内水分只受扩散作用的迁移规律。文献指出温度梯度不仅引起粮堆内的热量传递,而且影响了其内水分的迁移和再分配,即所谓的索瑞特效应。M.Prakash等[5]借助计算流体力学模拟软件(CFD)建立了吸湿性多孔介质在自然对流条件下的热质传递模型,该文献描述了一个紊流叠加饱和吸湿性多孔介质系统的热湿传递。
我国对于储粮生态系统的热湿耦合研究起步较晚,多为现场实地调研。王远成[6-7]对粮食存储的热湿传递问题有较多研究,一方面,通过对小麦、玉米等谷物的热物性测试、计算获得了小麦、玉米等谷物的比热及导热系数;在数值模拟方面,基于吸湿和解吸湿相变理论和局部热质平衡原理,提出了涉及对流和扩散的描述深层粮堆内部热湿耦合传递规律的模型,并借助计算流体动力学技术(CFD)模拟了仓储粮堆内温度和湿度随仓外气候改变的变化规律。
基于国内外对仓储粮堆内传热传质问题的研究现状,本研究以仓储粮堆内局部热湿传递过程作为研究对象,研究近似冬夏季工况下粮堆内温湿度的动态变化规律,充分考虑了仓储粮作为吸湿性多孔介质具有复杂的热源、湿源。
2 仓储粮堆内热湿耦合传递机理的研究
对于仓储粮堆内热湿耦合传递机理的研究是繁琐深奥的。因为对仓储粮堆内热湿传递的影响因素是多方位的。除了仓储粮品质和温湿度以外,还有粮仓存储大小、仓外温湿度、大气压力、太阳辐射强度和粮仓气密性都会对仓内热量传递和水分迁移再分配产生影响。其详细表示如图1。一方面,由于外界气温的昼夜和季节变化,粮食不断的通过外围护结构于外界进行热量交换,另一方面,考虑到粮食存在热惰性,鉴于上述两方面的原因,在粮堆内部易形成温度梯度。在温度梯度的影响下,会在粮堆中产生于温度梯度同向的水蒸汽压力梯度,由于粮食颗粒具有吸湿和解吸湿特性,最终导致水蒸汽在粮堆内扩散,引起水分迁移和再分配。
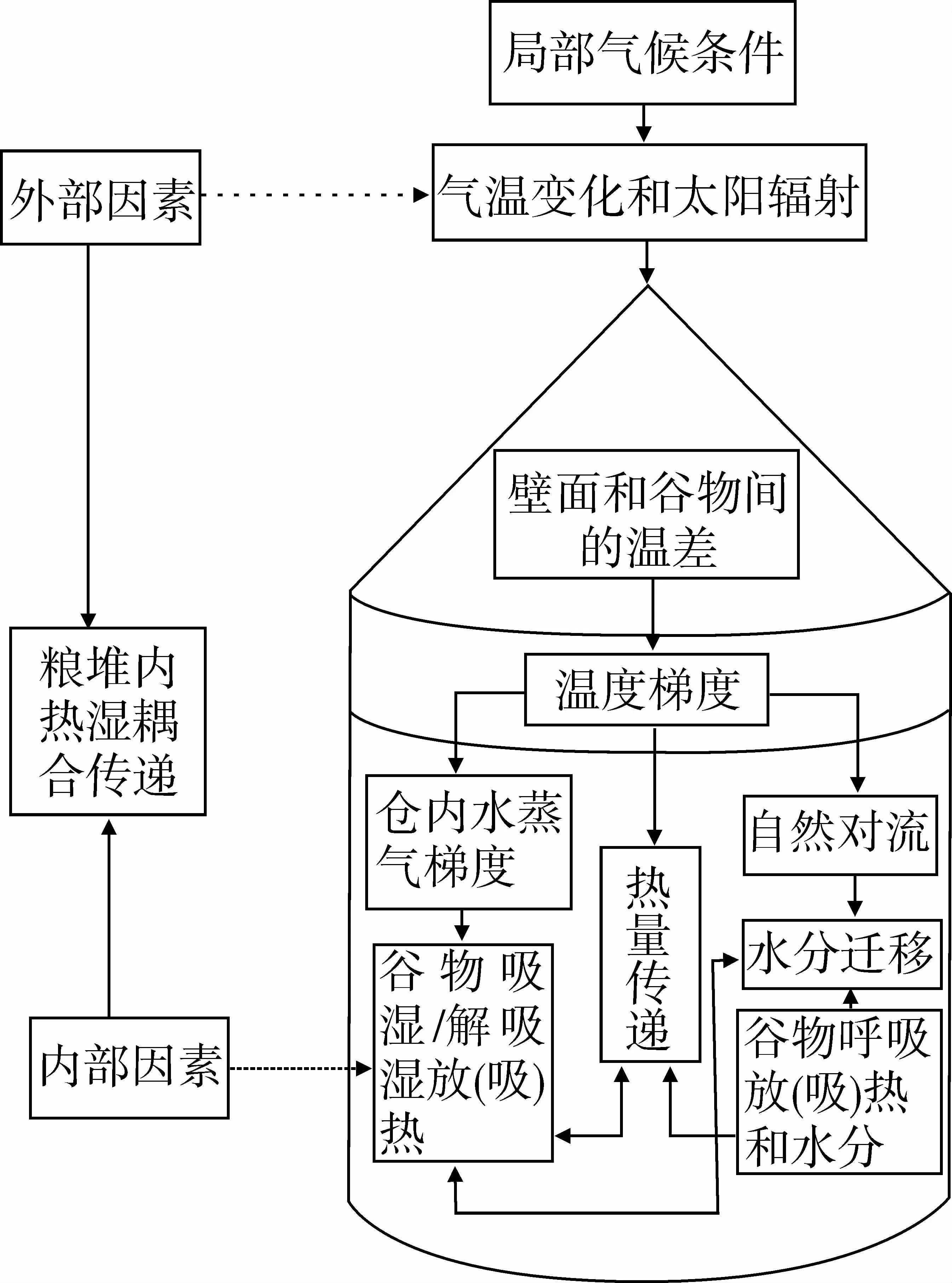
图1 仓储粮堆内热湿耦合影响因素详解
对于此热湿传递现象的后果是:其一,粮仓会在局部形成高温高湿区域,不仅为病菌和害虫提供更好的生存条件,而且引起粮食霉变和呼吸加剧损耗干物质;其二,由于局部气候条件的不同可能在粮仓局部形成低温高湿区域,只要其温度低于露点温度就会产生结露现象,加剧粮食颗粒的霉变,严重可能裂变成颗粒发芽现象。一般对于仓储粮堆来说,粮食颗粒都是随机的静态储藏。在一定温度下,会在粮食颗粒表面形成水蒸汽吸附边界层,当仓内水蒸汽压力大于颗粒表面水蒸汽吸附压力时,颗粒缝隙中的水蒸汽会源源不断的进入粮食颗粒内,即所谓的粮食吸湿作用;当仓内水蒸汽压力小于颗粒表面水蒸汽吸附压力时,颗粒中的水分会通过毛细管扩散到颗粒缝隙中,即所谓的粮食解吸湿作用。
3 吸湿性多孔介质热湿耦合传递的数学模型
本研究基于表征体元(REV)和局部热质平衡原理,考虑到粮食颗粒的吸湿和解吸湿特性以及由于温度梯度产生的仓内空气的自然对流的影响,并将热湿效应和湿热效应考虑其中,采用有限元法求解双区域热湿耦合模型。假设本研究研究的多孔介质是连续性的、均匀分布的气固两相。假设粮食颗粒之间缝隙中的空气由于粮堆温度变化而引起的空气扰动,形成一定的浮升力。
3.1 多孔介质区域
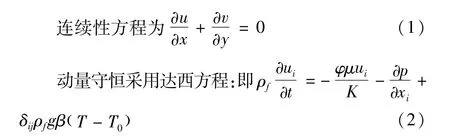
基于本研究对象是封闭粮仓,粮堆被看作是吸湿性多孔介质,其存在气固两相(气相为粮粒缝隙中的空气,固相为粮食颗粒),对于粮堆应用能量守恒涉及空气和粮粒的物性参数,所以为了求解方便采用等效方式。如:ρbulk=ερair+(1-)ερgrain;Cbulk=εCair+(1-)εCgrain;kbulk=εkair+(1-)εkgrain。下述为能量守恒方程,即
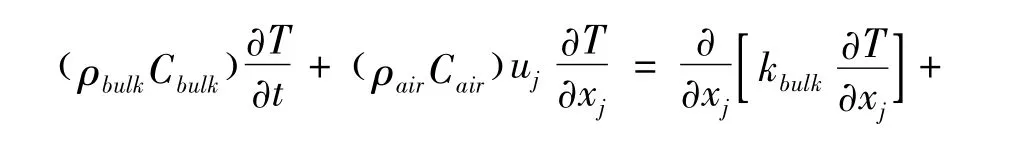

其中方程右侧最后一项是表示粮粒的吸湿解吸湿特性。其作为源项表示单位体积条件下谷物水分的凝结或蒸发相变潜热,hfg假定为常数为2476.55 kJ/kg;此研究将粮粒呼吸产热忽略在外。小麦的热物性参数:
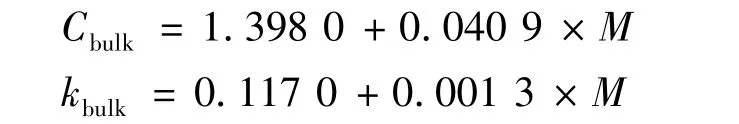
式中:M表示含湿量,M=Wg/(1+Wg)×100。
水分平衡方程为
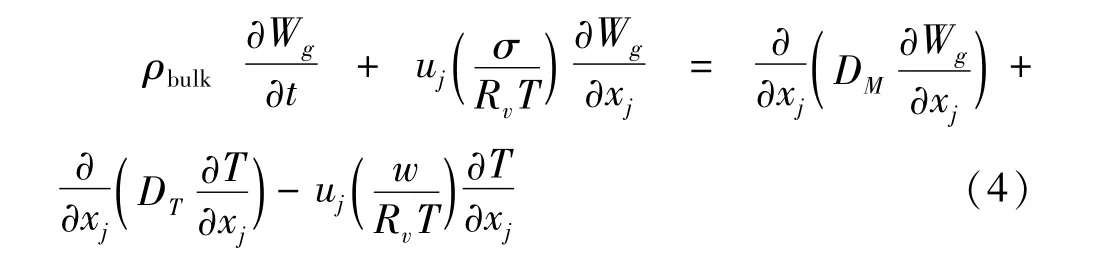
3.2 空气区域
鉴于在竖直方向上存在浮升力,且流动为湍流自然对流,所以其动量方程采用Navier-Stokes方程。

k-ε方程:
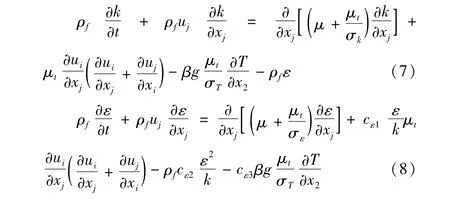
3.3 数学模型有效性的验证
该文的数学模型有效性通过相似原理与外国文献和试验数据的比较验证。Anderson等[8]以小麦为对象构建了如图2所示的试验台研究对流扩散情况下的水分迁移规律。Anderson搭建的试验模型为可以容纳450 kg小麦、容积为0.57 m3的长方体仓,其中初始时刻小麦的湿基水分为14.6%,边界条件为只在水平方向存在温度梯度、上下边界为绝热边界,各个边界设定为不可渗透边界。试验观测周期为316 d。结合试验台上的观测点,得到相应的数据表(见表1)。
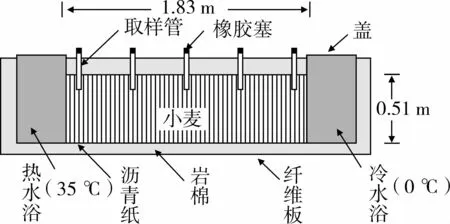
图2 水分迁移试验台
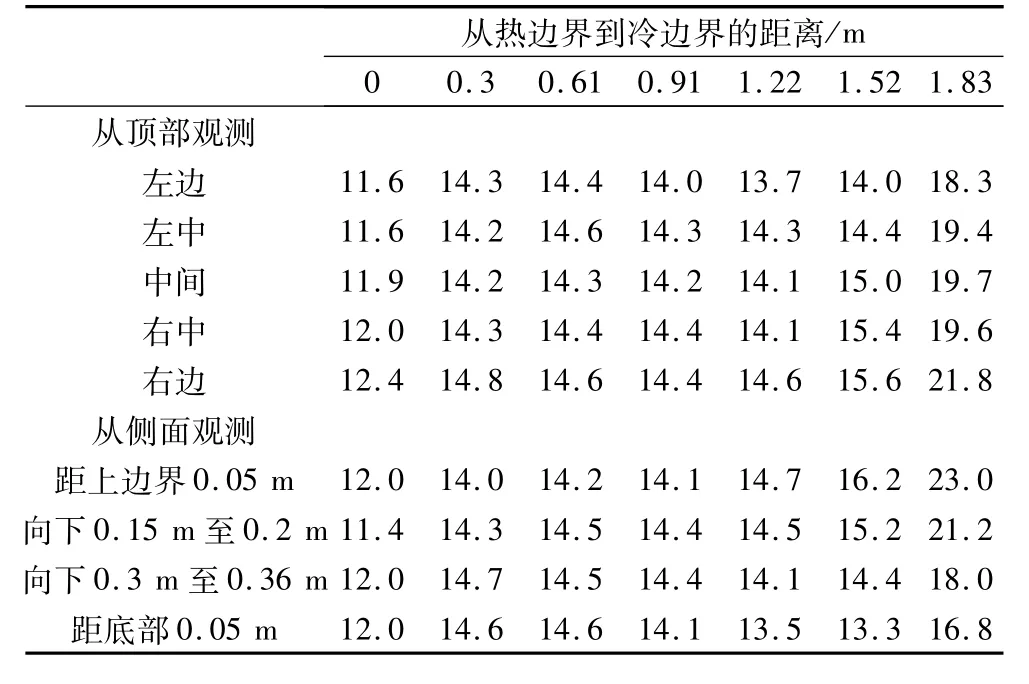
表1 平均含水量(%湿基)
本研究以初始粮温与气温的差值产生的梯度作为驱动力诱导粮仓内水分的迁移,研究比较周期里的水分瞬态变化,为方便比较,只取150 d的变化趋势,研究成果与K.K.Khankari的模拟结果和Anderson的试验结果进行比较如图3,可以发现结果基本吻合,所以可以验证上述数学模型的有效性。
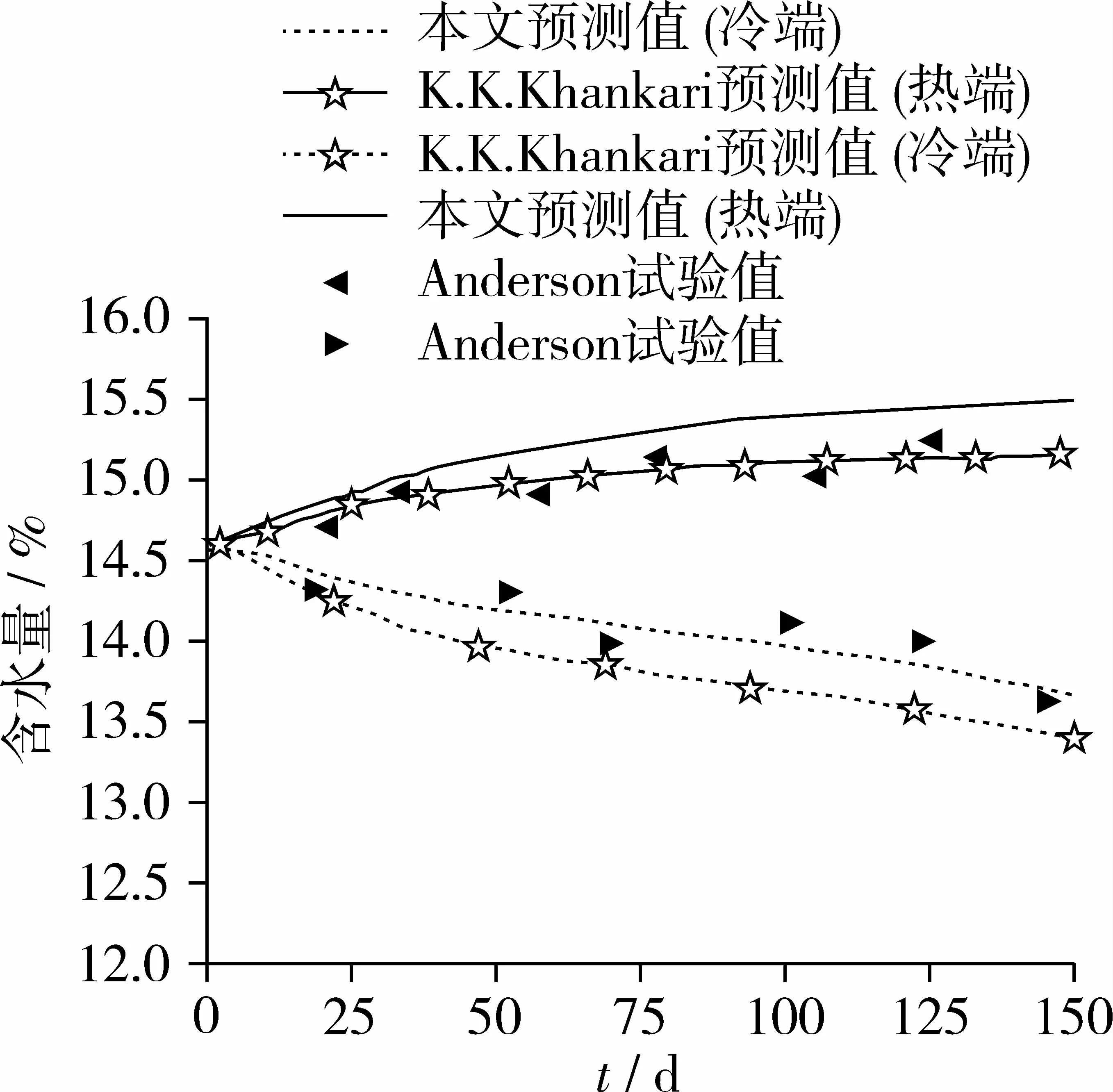
图3 模型有效性湿度瞬态变化比较
4 吸湿性多孔介质热湿耦合传递的物理模型和模拟条件
本研究以圆柱形仓储小麦粮堆内局部热湿传递过程作为研究对象,鉴于粮仓为圆柱形结构符合轴对称原理,其示意图如图1,圆柱形仓储粮仓下部分区域是仓储小麦的粮堆区域,上部分区域是用于机械排风的空气区域。且粮仓内的各个物性参数和变量都满足对称规律,所以为了加快多物理场数值模拟软件(COMSOL)的运算速度,将物理模型选定为圆柱形粮仓轴向截面的一半,如图4。其几何尺寸定义为:径向宽度R=5 m,粮堆高度L1=10 m,粮仓外侧高度L2=12 m,粮仓轴向高度 L3=16 m。对于抽象复杂的问题研究简单的依靠几个偏微分方程和物理模型是远远不够的,还需要一定的辅助条件。常见的辅助条件有初始条件和边界条件。传热学中指出边界条件分为3类:第1类是定常条件,如给定恒定温度恒定速度,也成为Dirichlet条件;第2类是给定一通量值,如给定边界零通量边界,也称为Neumann条件;第3类是混合边界条件,也称为Robin条件。本研究只涉及前两类条件,对第3类该文不做介绍。
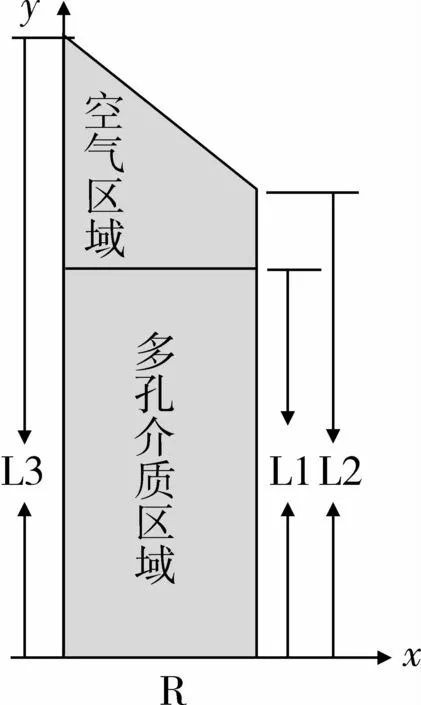
图4 圆柱形粮仓轴向截面几何尺寸
对于该文物理模型在二维笛卡尔坐标系下的边界条件设定为粮仓底部表面设定为热湿绝缘,轴线处由于考虑轴对称原理其温度梯度和水分梯度为零,粮仓顶部和侧面于外界大气接触设定为定温条件,各边界面上都是非流动、不可渗透边界,特别提示在空气区域和多孔介质区域交界面处只考虑热量交换而忽略水分迁移。用数学语言描述如下所示:

5 模拟结果及分析
对于模拟工况可以划分成冬季粮堆(热芯粮)和夏季粮堆(冷芯粮)两大类。基于冬季时期粮堆温度大于外界气温,随着时间推移温度梯度逐渐形成,进而产生了上述所述的温度梯度和水分梯度,最终导致粮温由外到内逐渐降低,粮堆内水分发生迁移和再分配;类似夏季时期粮堆温度小于外界气温,最终导致粮温由外到内逐渐升高。
5.1 相同初始水分(湿基水分)不同温差(温度K)粮堆内温度和水分分布规律

图5 相同湿基水分不同温差下热芯粮堆内温度、水分变化比较图
通过图5可看出在相同湿基水分条件下模拟150 d后2种工况的的温度场趋势大体相同,对于空气区域基本已经冻透,由于粮堆具有热惰性,所以多孔介质区域的温度场的变化趋势没有空气区域明显,粮堆轴心处依然保持原有温度,但鉴于两模拟工况的温度梯度不同,工况2粮堆内的温度梯度较工况1大,且模拟时间较短,粮仓内部轴心处的热量还没有传递到粮仓外,所以粮堆2内小麦维持在原状态的区域要明显少于粮堆1,且保持原工况的区域集中于粮堆的顶部轴心处;从图5c,图5d比较可知,温差大小影响水分迁移的速度,不同储粮部位的温差越大,水分迁移幅度越大。通过图5c图例可知,最低含水量和最高含水量差值为1.980%,通过图5d图例可知,最低含水量和最高含水量差值为11.497%。因此,当外界气温与粮堆温度相差较大时,导致局部粮堆水分增幅过高,可能引起粮堆内局部计算区域的水分含量超出安全储藏值,导致此区域粮食因为水分过高而产生发芽、霉变等影响粮食品质的现象。
5.2 相同温差(温度K)不同初始水分(湿基水分)下粮堆内温度和水分分布规律
通过图6可以发现相同温差不同湿基水分条件下温度场的变化规律大体相同,水分含量对于粮仓内温度的变化影响不大,都是模拟150 d后在粮仓轴心处维持在温度292.88 K,表明粮仓中心位置基本没有温度变化,简单从温度场角度看,只要粮食收获干燥达到安全存储指数,中心位置的粮食品质没有变化;通过图6c、图6d可知,在存储期内对于热芯粮其水分迁移大体方向是一致的,同理,冷芯粮的水分迁移位置也是一样的,通过图例可知在湿基水分为14%初始粮温293.15 K初始气温273.15 K条件下粮堆内含水量最大差值为1.980%,湿基水分为16%初始粮温293.15 K初始气温273.15 K条件下粮堆内含水量最大差值为2.585%。因此,粮食湿基水分较大的粮仓在存储期内易超出粮食的安全存储指标。
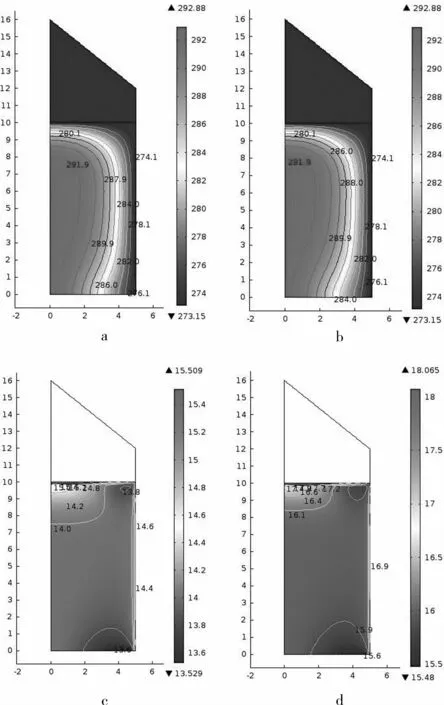
图6 相同温差不同湿基水分下热芯粮堆内温度、水分变化比较图
5.3 相同初始水分(湿基水分)相同温差(温度K)下粮堆内温度和水分分布规律
工况1表示的是夏季冷芯粮,工况2表示的是冬季热芯粮。图7a空气区域没有等温度表示150 d时其温度与外界气温相等,由于粮仓底面是绝热的,所以无论是夏季工况还是冬季工况在多孔介质区域内的下半部分只存在水平方向上的温度梯度,在其上半部分既有水平方向的温度梯度又有竖直方向的温度梯度;对于夏季工况,水分分别沿着多孔介质区域的右下部分和顶部右侧向其侧边界面和顶部内侧迁移,进而在这些区域形成高温高湿区,最终导致结顶现象发生,对于冬季工况,水分分别沿着多孔介质区域的底部边界和顶部右侧向其侧边界面和顶部内侧迁移,进而在这些区域上形成狭窄的低温高湿区。对于湿基水分为14%夏季冷芯粮来说,在150 d存储期内其含水量变化范围为7.896%~15.247%,最大差额为7.351%;对于湿基水分为14%冬季热芯粮来说,在相同存储期内含水量变化范围为12.859%~24.356%,最大差额为11.497%;而且夏季冷芯粮表现出较低的含水量(最低值为7.896%),在计算区域局部形成低湿地带;冬季热芯粮表现出较高的含水量(最高值为24.356%),在计算区域局部形成高湿地带。因此,比较冬夏季粮堆内温度和水分分布情况可知,夏季粮堆存储较冬季容易,但综合温度和水分分布图,夏季在计算区域低端右侧易发生结露现象,冬季在存粮顶端轴心处易发生结顶现象,在低端右侧可能产生结露现象。
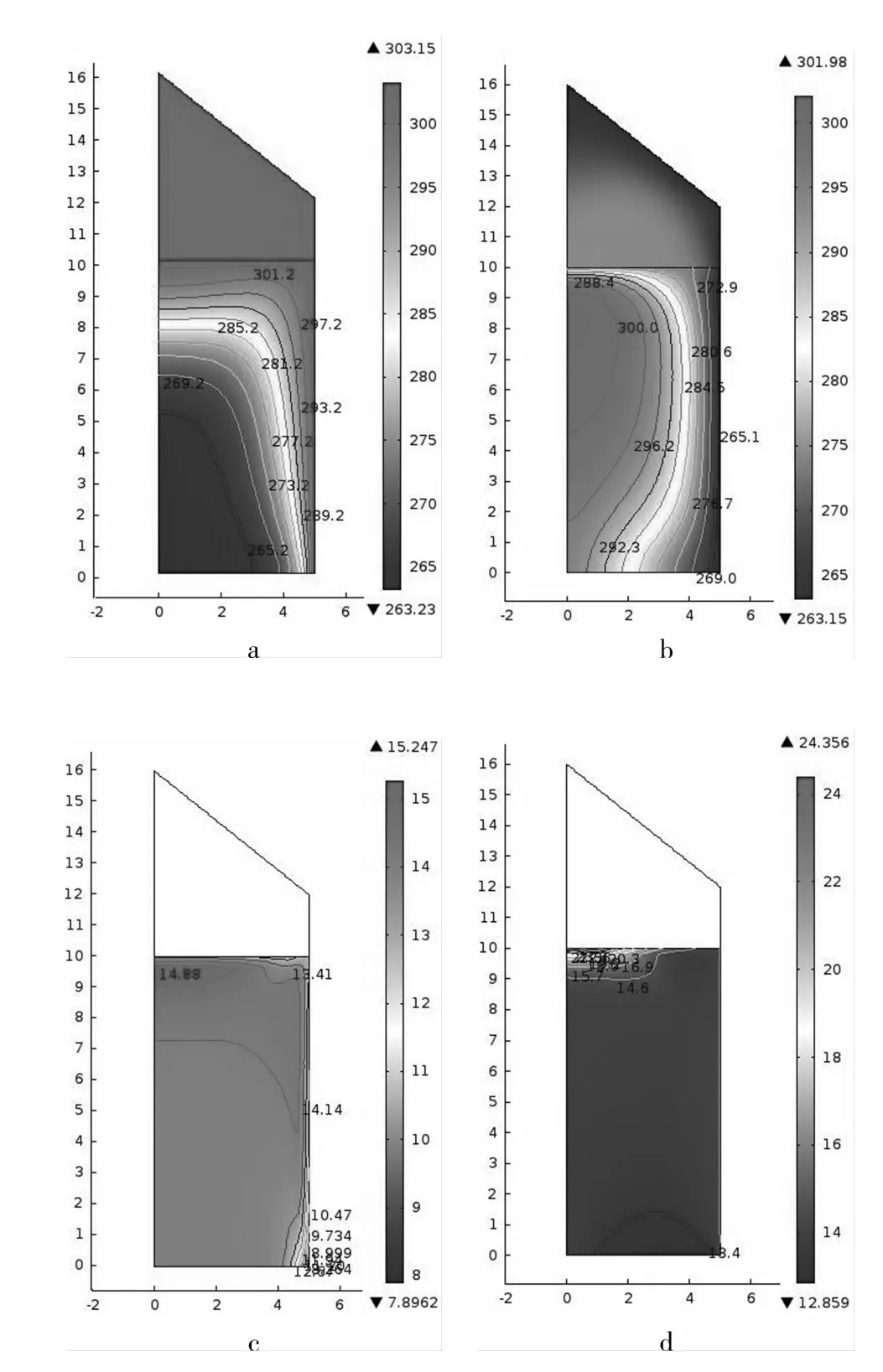
图7 相同温差相同湿基水分下冷热芯粮堆内温度、水分变化比较图
6 结论
该文通过建立简单的圆柱形存储粮仓热湿耦合数学模型,借助多物理场数值模拟软件(COMSOL)求解,得出密闭粮仓内的温度和水分分布规律,通过瞬态模拟结果指导现实粮仓的工程实例。通过上述模拟结果可以得到以下结论:
6.1 通过对相同温差不同初始水分(湿基水分)工况下温度和水分分布规律研究可知,湿基水分为14%初始粮温293.15 K初始气温273.15 K条件下粮堆内含水量最大差值为1.980%,湿基水分为16%初始粮温293.15 K初始气温273.15 K条件下粮堆内含水量最大差值为2.585%,所以粮食在收获干燥之后应尽可能的降低其水分含量,只有这样才能保证在粮食在存储期间内粮堆内水分迁移量减少至最低值,确保粮食尽可能的在安全存储指标之内。
6.2 通过对相同初始水分(湿基水分)不同温差工况下温度和水分分布规律研究可知,湿基水分为14%初始粮温293.15 K初始气温273.15 K条件下最低含水量和最高含水量差值为1.980%,湿基水分为14%初始粮温303.15 K初始气温263.15 K条件下最低含水量和最高水分含量差值为11.497%,所以粮食在存储期间要尽量减少粮温和外温的差值,因为导致粮堆内热湿耦合传递的本质驱动力是温度梯度,温度梯度减小了,可以保证水分迁移量减少,同时也降低了粮仓内局部结霜现象发生的可能性。
6.3 通过相同初始水分(湿基水分)相同温差近似冬夏季工况下温度和水分分布规律研究可知,对于湿基水分为14%夏季冷芯粮来说,在150 d存储期内其含水量变化范围为7.896%~15.247%,最大差额为7.351%;对于湿基水分为14%冬季热芯粮来说,在相同存储期内含水量变化范围为12.859%~24.356%,最大差额为11.497%,粮食夏季存储其安全指数比冬季存储指数高。冬季工况易在粮堆顶端轴心处发生结顶现象。
[1]Fuji Jian,Digvir S.Jayas,Noel D.GWhite.Temperature fluctuations and moisturemigration in wheat stored for 15 months in ametal silo in Canada[J].J.Stored Prod.Res.,2009,45:82-90
[2]Ruska Laszlo,Timar Adrian.Simulation of changes in awheat storage bin regarding temperature International Symposia Risk Factors for Environment and Food Safety&Natural Resources and Sustainable Development,Faculty of Environmental Protection[C].Oradea,2009:276-282
[3]Ali M SAI-Amri,Sirelkhatim K Abbouda.Application of a Mass Transfer Model for Simulation and Prediction of Moisture Distribution in Stored Corn Grains[J].Scientific Journal of King Faisal University(Basic and Applied Sciences),2004(5):197-213
[4]K K Khankari,R V Morey,S V Patankar.Mathematical model formoisture diffusion in stored grain due to temperature gradients[J].Transactions of the ASAE.1994,37(5):1591-1604
[5]Mahesh Prakash,Yuguo LI.CFD modeling of natural convec-tion heat and mass transfer in hygroscopic porousmedia[J].Drying technology,2000,18(10),2175-2201
[6]王远成,段海峰,张来林.就仓通风时粮堆内部热湿耦合传递过程的数值预测[J].河南工业大学学报:自然科学版,2009,30(6):75-79
[7]王远成,张忠杰,吴子丹,等.计算流体力学技术在粮食储藏中的应用[J].中国粮油学报,2012,27(5):86-91
[8]Anderson JA,JD Babbitt,W O SMeredith.The effect of temperature differential oil the moisture content of stored wheat.Can.J.Res.,1943,21(c):297-306
[9]王殿轩,李兆东,陆群,等.不同温度下米象的运动行为研究[J].河南工业大学学报:自然科学版,2011(4):10-13.
Research of Closed Silo Stored Grain in the Natural Convection and the Coupled Heat and Moisture Transfer
QiWei1Wang Yuancheng1,2Bai Zhongquan1Zhang Zhongtao1
(School of Thermal Energy Engineering,Shandong Jianzhu University,Jinan 250101)(Key Laboratory of Renewable Energy Utilization Technologies in Buildings,Ministry of Education2,Jinan 250101)
The grain is a kind of hygroscopic porous medium with characteristics ofmoisture absorption and moisture absorption.After harvest,the grain are stored in a closed non natural storage ventilation condition formost of time.In view of the seasonal and diurnal variation of granary and climatic conditions,temperature and humidity willmake a circled alteration on the grain heap and have effects on the storage security.The paper has taken the grain storage in local coupled heat and moisture transfer process as the research object,utilizing numerical simulation software ofmulti-physics field(COMSOL)for numerical simulation,to research the approximate dynamic changes in winter and summer on grain temperature and humidity;to give full consideration to the grain storage as a hygroscopic porousmedia with complex heat,moisture source conditions.
hygroscopic porous,media coupled heat and moisture transfer,numerical simulation ofmultiphysics field,cylindrical grain storage,natural convection
TS210.3
A
1003-0174(2015)10-0083-07
国家自然基金(51276102),山东省自然基金(ZR2011 EEM011)
2014-04-10
亓伟,男,1987年出生,硕士,生物性多孔介质传热传质研究
