改进R-D算法的ISAR成像仿真研究

李文静，陈红卫

(江苏科技大学 电子信息学院，江苏 镇江212003)

0 引 言

逆合成孔径雷达 (Inverse Synthetic Aperture Radar，ISAR)是一种重要的微波探测工具，在国土防御、空间探测等领域发挥着重要的作用［1］。它不仅具有全天时、全天候、远距离探测和识别非合作运动目标的能力，而且能够对导弹、卫星、飞机、舰船、天体等运动目标进行远距离成像。

逆合成孔径成像的主要任务是对完成运动补偿的回波信号进行相干积累，从而重建目标散射点的空间分布。目前在逆合成孔径雷达中使用的算法主要有距离多普勒算法、采用现代谱估计的超分辨算法［2］、基于压缩感知的成像算法、联合时频技术成像算法等。最经典的成像算法为距离多普勒(R -D)算法，此算法的运算量小，适合于实时处理，容易物理实现［3］。但算法要求散射点的多普勒频率在相干积累时间内近似为常数，这种假设只有对平稳目标或者目标小转角成像的情况下近似成立，因此采用R-D 算法获得的图像横向分辨率通常较低。距离-多普勒算法只适用于小转角和平稳目标成像(3° ～5°)。

针对基本R -D 算法存在的不足，本文采用脉冲压缩技术、插值技术、极坐标格式、后阈值处理技术以及窗函数特性改进R -D 成像算法，并对算法进行仿真验证。

1 ISAR 成像的原理

1.1 ISAR 成像系统

逆合成孔径雷达的成像系统一般是目标运动、雷达静止。图1 示意了ISAR 的成像系统。雷达发射机发射信号，发射信号经空间目标返回形成回波信号，雷达接收机接收回波信号，成像系统从回波信号中提取信息、显示运动目标。ISAR 成像空间目标的表面特性复杂且转过的角度很小，通常可以近似看成是由很多不同位置、不同反射系数的散射点构成。ISAR 成像的目标就是要正确显示出各散射点的相对位置及其回波强度。

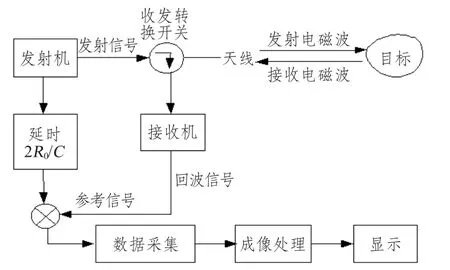
图1 ISAR 成像系统Fig.1 The system of ISAR imaging

1.2 ISAR 成像的等效转台模型

目标和雷达之间的相对运动可分为平动和转动:平动对成像没有贡献，成像前需进行运动补偿;在转动中，散射点沿纵向的位移是产生散射点多普勒频移的基础。转台成像是假定目标放置在一个转动的平台上，目标相对于雷达视线只有旋转运动。图2 为转台成像的几何关系［4］。图2 中，x － o － y 为目标坐标系;u －o －v 为雷达观测坐标系;R0为目标和雷达间的距离;θ 为目标旋转角度;ω 为绕轴心转动匀速角速度，理想情况θ=ωt;(x，y)为目标上一个散射点的坐标;R(θ)为点(x，y)到雷达的距离。当ISAR 满足远场条件和小角度成像条件时，R(θ)可以近似地表示为:

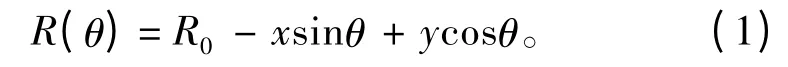
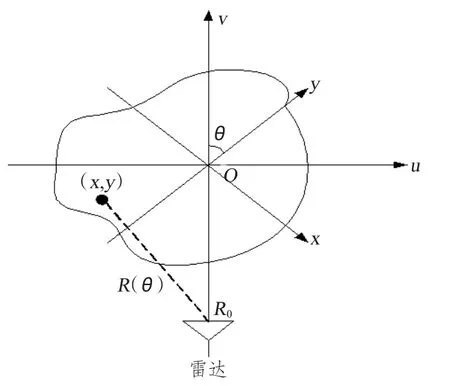
图2 转台成像的几何关系Fig.2 The geometry relation of turntable imaging

假设雷达发射信号为Et=exp(jwt)，目标的距离尺寸为2L，(x，y)散射点的理想模型为g(x，y)，波长为λ，则去载频相位项和固定延迟项R0后，雷达接收到的基频回波可以表示为:

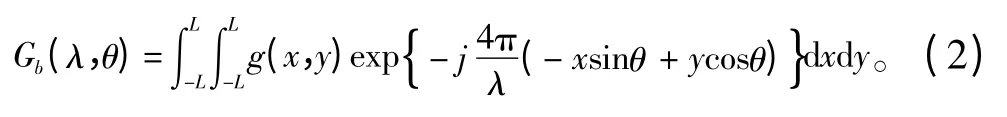
式(2)表明，雷达成像所需要的信息从2 个方面获得:一是对不同波长下的雷达回波信号进行处理得到目标一维距离向轮廓，为满足距离向的高分辨率要求需使用宽带多频信号;二是对不同旋转角θ 的目标回波进行处理得到目标的方位向轮廓，这要求目标有绕其轴心的转动［5］。

1.3 ISAR 的R-D 成像

ISAR 利用R -D 进行成像，R -D 成像算法是基于目标均匀旋转模型的一种经典的算法［6］。目标上散射点相对于雷达的径向运动速度决定了回波信号的多谱勒频率。

假设对回波信号的处理在t = 0 附近较小时间间隔内进行，即θ ≈0 ，则由式(1)和式(3)可得式(4)和式(5)。由式(4)和式(5)可知，回波信号的多普勒频率和距离延时可确定散射点(x，y)的位置。

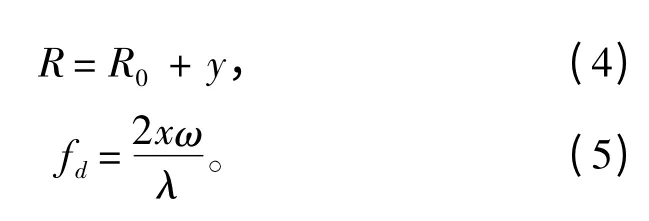
2 改进的R-D 算法

2.1 线性调频信号的脉冲压缩

为解决雷达系统中作用距离和分辨率之间的矛盾，可采用脉冲压缩技术。即发射时采用宽脉冲信号，接收时采用相应的脉冲压缩法来获得窄脉冲。脉冲压缩技术较多，如直接相关法、快速傅里叶变换法、频域分析法等。线性调频(Linear Frequency Modulation，LFM)信号的脉冲压缩技术包含:匹配滤波处理和解线频调处理。

匹配滤波的基本思想:雷达发射端发射一个中频经过线性频率调制的宽脉冲信号，在接收端雷达将接收到的目标回波信号通过一个与发射信号相位共轭匹配的压缩网络。匹配滤波脉压处理过程如图3(a)所示。解线频调脉压根据线性调频信号特性提出，其基本思想是将回波信号与本振信号进行差拍处理。解线频调处理的流程如图3(b)所示。

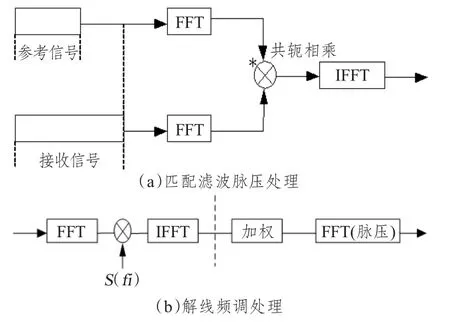
图3 匹配滤波脉压处理与解线频调处理Fig.3 Match the pulse compression and dechirping

图4 是雷达检测2 个RCS 分别为σ1= 1 m2，σ2= 0.5 m2的目标回波未经压缩和经压缩的2 种情况。这2 个目标在时间上的间隔不足以被分辨，图4(a)中也显示了2 个目标的合成回波信号是重叠的，无法分辨。但经脉冲压缩以后，2 个脉冲完全分开，2 个目标可以被分辨。由此可看出脉冲压缩技术的优点［7］。

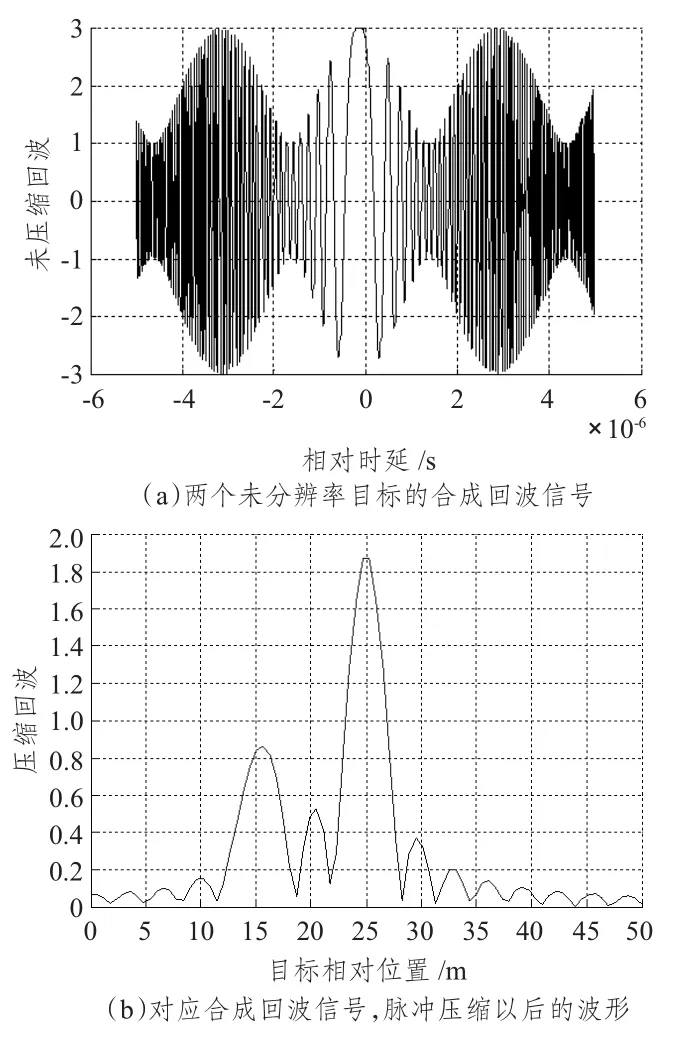
图4 脉冲压缩技术在雷达系统中的应用Fig.4 Pulse compression applied in the radar system

2.2 基于LFM 回波模型的R-D 算法

ISAR 系统发射的LFM 信号为

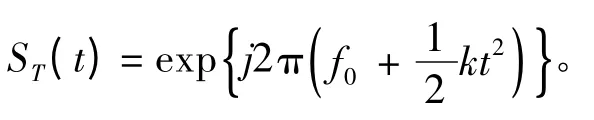
式中:f0为载波频率;k 为调频斜率。

则距离雷达为R 远处的点目标回波信号可记为式(6)。将式(6)的目标回波信号和参考信号进行混频，并对整个目标区域进行积分，回波信号简化后可用式(7)表示。式中g(x，y)和G(fx，fy)是一对二维傅里叶变换对。若G(fx，fy)在(fx，fy)平面上的值已知，则g(x，y)可以通过对G(fx，fy)取二维傅里叶逆变换而得到。R -D 成像算法示意如图5所示。

在ISAR 成像系统中，雷达从一个方向角向目标发射一个LFM 并接收回波，然后在下一个方向角依次重复这个过程，从而获得一个二维数据集，第一维距离向为LFM 波调频频率，第二维方位向为目标旋转角。

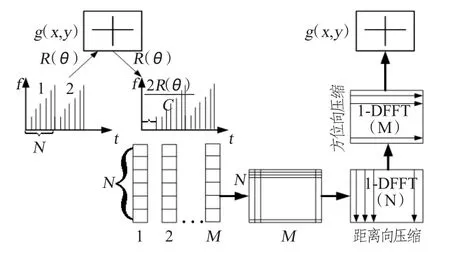
图5 R-D 成像算法示意图Fig.5 The chart of R-D imaging algorithm

2.3 R-D 算法中加权窗及后阈值处理

一般的R-D 算法中，由于sinc 函数的副瓣较高，二维场景成像得到的图像较模糊。为克服此缺点，可在R-D 算法中采用加权技术，展宽主瓣抑制旁瓣。ISAR 成像中获得的散射点数据集已经离散化，可利用离散傅里叶变换 (Discrete Fourier Transform，DFT)。加权技术可采用加权窗函数完成，常用的加权窗函数有矩形窗函数、三角窗函数、Hanning 窗函数、Hamming 窗函数、Kaiser 窗函数和Blackman 窗函数等。表1 列出了几种窗函数的特性比较［8］。

后阈值处理是在目标图像输出前进行的处理。首先选择合适的阈值，然后根据阈值进行处理，对大于阈值的维持原有值，对小于阈值的用0 值替换。

表1 窗函数特性比较Tab.1 Comparative characteristics of different windowing function

2.4 R-D 算法中的极坐标格式

R-D 算法适用于转角较小的情况，当转角过大时散射点发生越分辨单元走动，造成重建图像的模糊。为解决这个问题，可采用极坐标格式算法。它是用极坐标格式记录频率空间观测样本，将极坐标系转化为直角坐标系，对距离向和方位向进行插值，最后利用二维傅里叶变换完成成像过程，实现大转角情况下成像。极坐标格式算法(PFA)的流程如图6 所示。插值方法有最近邻插值、线性插值、多项式插值、三次样条插值等。一般来说插值方法的阶数越高，成像质量也越好，但计算量相应增大。

图6 PFA 算法的流程Fig.6 The process of PFA algorithm

3 仿真实验与结果

3.1 仿真算法实现

根据目标的旋转角度大小情况分别处理雷达回波信号。一种情况是目标尺寸不大，在3° ～5°之间的较小转角成像，另一种情况是较大转角成像。其流程如图7 所示。

图7 本文仿真算法流程Fig.7 The algorithm process in this paper

3.2 仿真目标模型与雷达参数

仿真目标模型是由110 个散射点组成的飞机形状，长度为18 m，宽度为16 m，其散射点模型如图8 所示。雷达的带宽为525 MHz，中心频率为8 GHz。小角度转动范围为4.23°;大角度转动范围为-30°。

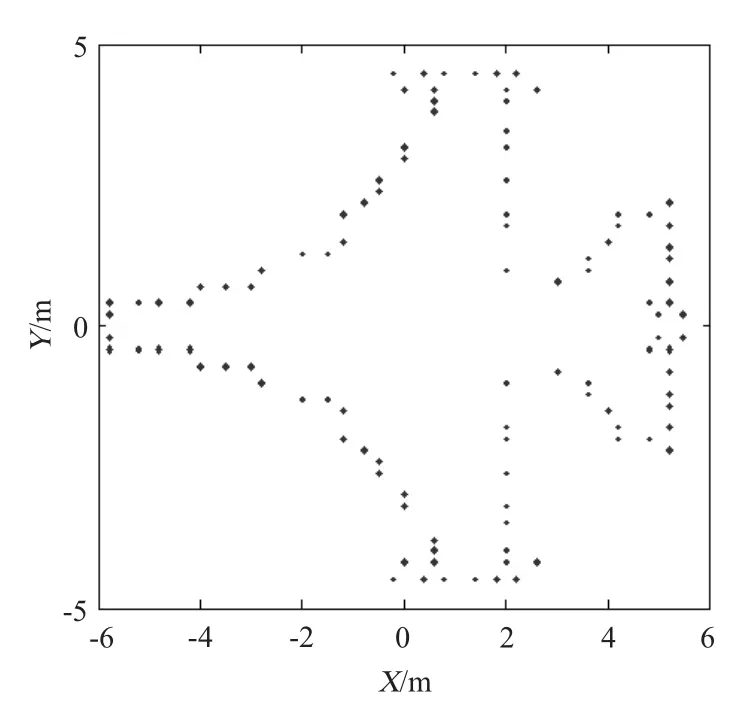
图8 仿真用的散射点模型Fig.8 The model of simulation

3.3 仿真结果

仿真结果如图9 所示。其中图9(a)是在小转角情况下基本R-D 算法的成像结果，图9(b)是在小转角情况下本文算法的成像结果。图10(c)是在大转角情况下本文算法的成像结果。

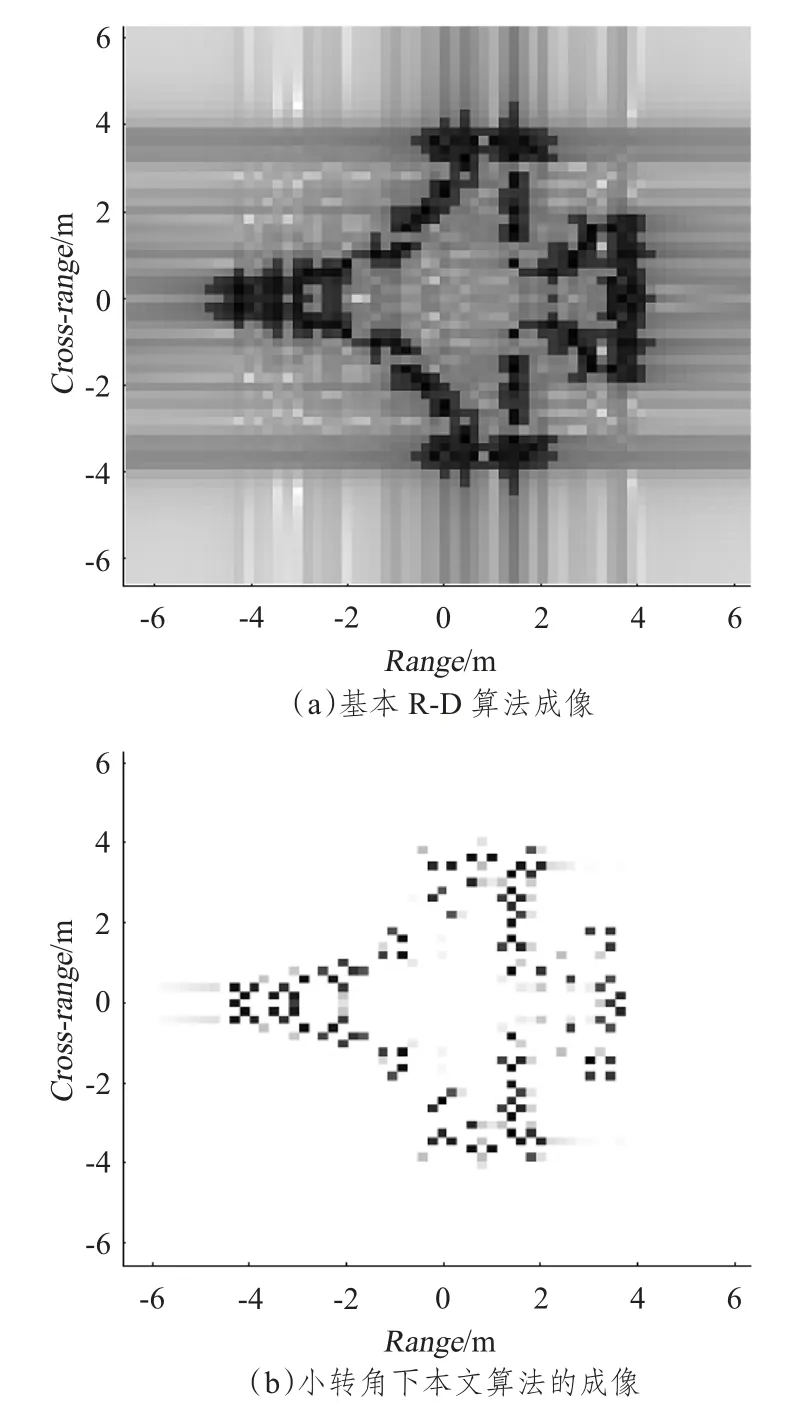
图9 成像结果比较Fig.9 The compare of imaging result

图10 大转角下本文算法的成像Fig.10 The imaging in the large rotation angle

图9(b)成像中采用了Kaiser 窗函数，函数中α =3 取值不同会导致展宽主瓣和抑制旁瓣的效果不同，文中经对比选用α = 3 。图10 (c)成像中采用了8 点sinc 插值方法的极坐标格式算法。

4 结 语

在ISAR 成像中，R -D 算法以其高效、实用得到广泛应用。本文在基于R -D 算法基础上，研究脉冲压缩技术、后阈值处理技术、插值技术、极坐标格式以及窗函数特性在R -D 成像算法中的应用。当转角较小时，采用脉冲压缩技术、加权技术和后阈值处理技术改进R -D 算法;当相干积累角度增大，即转角较大时采用插值技术和极坐标格式改进R-D 算法。并采用二维目标飞机散射点模型对改进算法进行仿真，仿真结果表明算法的有效性。

［1］王虹现.ISAR 成像新方法研究［D］. 西安:西安电子科技大学，2010.WANG Hong-xian. The new imaging method of inverse synthetic aperture radar［D］.Xi′an:Xidian University，2010.

［2］白雪茹.空天目标逆合孔径雷达成像新方法研究［D］.西安:西安电子科技大学，2011.BAI Xue-ru. Space target inverse synthetic aperture radar imaging research new methods ［D］. Xi′ an:Xidian University，2011.

［3］李宁.逆合成孔径雷达成像方法研究［D］.南京:南京航空航天大学，2011.LI Ning. The research of inverse synthetic aperture radar imaging method ［D］. Nanjing:Nanjing University of Aeronautics and Astronautics，2011.

［4］刘永坦.雷达成像技术［M］.哈尔滨:哈尔滨工业大学出版社，2003.

［5］王桦.微波成像算法研究与仿真［D］.西安:西北工业大学，2006.WANG Hua.Research and simulation of microwave imaging algorithm ［D］. Xi′ an:Northwestern Polytechnical University，2006.

［6］林翊青，李景文.大距离徙动情况下距离多普勒(RD)算法与后向投影(BP)算法的比较［J］.雷达科学与技术，2004，2(6):349 -354.LIN Yu-qing，LI Jing-wen. The compare of RD algorithm and BP algorithm in large range migration［J］. Radar Science and Technology，2004，2(6):349 -354.

［7］MAHAFZA B R，ELSHERBENI A Z.朱国富，等，译.雷达系统设计MATLAB 仿真［M］.北京:电子工业出版社，2009.MAHAFZA B R，ELSHERBENI A Z. MATLAB simulation for radar system design［M］.Electronic Industry Press，2009.

［8］WILEY J，SONS.Inverse synthetic radar imaging with MATLAB algorithms［M］. First Edition，2012.