超磁致伸缩作动器的磁路设计与仿真分析

曹海龙，朱石坚，楼京俊，杨理华，李超博

(海军工程大学 动力工程学院，湖北 武汉430033)

0 引 言

传统的被动式隔振技术无法适应现代潜艇声隐身技术发展的要求，而不断发展的主动隔振技术为此提供了新的技术途径。作动器是主动隔振系统的核心部件，其精度和性能的优劣直接关系到整个控制系统的运行是否能够达到预定目标。超磁致伸缩材料(GMM)是一种新型的功能材料，它能有效地实现电能与机械能的相互转换，具有应变大、电能－机械能转换效率高、能量密度大、响应速度快等优点，因而在精密机械控制、机械传动机构传感器、水声换能器等技术领域有着广阔的应用前景［1－4］。利用超磁致伸缩材料制作而成的超磁致伸缩作动器(GMA)具有体积小、响应快，输出力和输出位移大等特点［5－6］，适合主动隔振系统的要求。但是GMA 的设计主要依赖于设计人员的经验，制约着高性能的GMA 的开发。本文通过Ansys 进行GMA 的仿真分析，可以得到磁轭材料对GMA 磁场均匀度的影响，能够更好地完成GMA 的设计。

1 GMA 的基本原理及磁路设计

1.1 基本原理

GMA 的结构一般有磁场施加系统、预应力施加系统及冷却系统［7］，其结构如图1 所示。

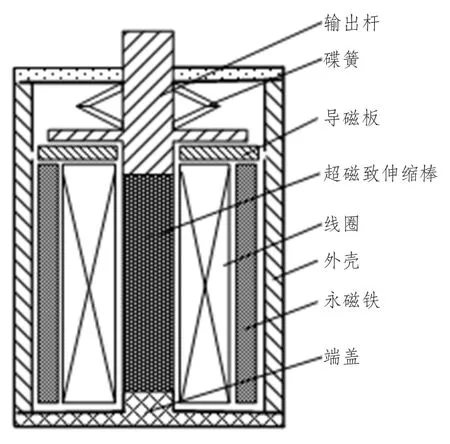
图1 GMA 结构简图Fig.1 The simple structure diagram of GMA

其基本工作原理为:以驱动线圈产生的磁场作为驱动磁场，在结构上由导磁材料制作的输出杆、导磁板及端盖，与GMM 棒形成闭合磁路［8］。当改变输入电流时，驱动线圈产生的磁场发生变化，由于GMM 棒的轴向磁致伸缩效应，GMM 棒即随之发生伸缩变形(即执行器输出位移和力)，从而实现电磁能向机械能的转换［6］。通过控制输入电流，可以控制执行器位移和力的输出。

磁路设计是为了设计一个低磁阻的磁路，把磁通量集中到GMM 棒的轴线上，使得GMM 棒上的磁场能量最大化，而在其他非工作区域尽量减小能量的损失，即减少不必要的漏磁［9－10］。

1.2 偏置磁场的选取

由图1 可知，GMM 棒的驱动磁场由线圈和永磁铁共同组成，其中永磁铁的作用是产生一定的偏置磁场使GMM 棒处于极化状态，避免倍频现象，改善作动器的线性特性。目前产生偏置磁场的方式主要有采用独立的直流螺线管线圈、在激励电流上叠加直流偏置分量及永磁铁3 种［11］。

采用独立的直流螺线管线圈或在激励电流上叠加直流偏置分量的方式，能够方便的调节偏置磁场，但是这2 种方式都会产生电阻损耗，从而使GMA 内部磁路的温度升高，影响GMA 的使用性能，同时在激励电流上叠加直流的方式会导致作动器轴向尺寸的增大。永磁铁产生的偏置磁场固定，其优点是:价格便宜;磁能积(BH)大;能提供所需的偏置磁场;工作稳定性好。故本文采用永磁铁来产生偏置磁场。

永磁铁的布置方式主要有如图2 所示2 种方式:图2(a)为利用圆筒形永磁铁产生偏置磁场，图2(b)为采用圆盘形永磁铁在端部产生偏置磁场。(a)方式获得的磁场强度较为均匀但磁阻较大，(b)方式易于获得较高的偏置磁场且磁阻较小，但其磁场均匀度要劣于(a)方式。采用高磁导率的磁轭材料可以减小磁路的磁阻，为了提高磁场的均匀度，本论文采用(a)图所示永磁铁的布置方式提供偏置磁场。

图2 永磁铁产生偏置磁场的方式Fig.2 The mode of permanent magnet generating bias field

1.3 GMM 棒的设计与选型

本文研究的作动器，主要工作在10 ～500 Hz 之间，属于中、低频驱动器，取GMM 棒的计算伸长量Δl 等于其设计最大输出位移xmax，则GMM 棒的计算长度为:

式中λj为磁致伸缩系数。

由于GMA 的设计指标为最大输出位移xmax=0.25 mm，当GMA 工作在线性区域时，取磁致伸缩系数λj= 3 × 10－3，则GMM 棒的计算长度lj=83.3 mm。由于受加工限制，GMM 棒需要特性的尺寸，将lj按所选GMM 棒的尺寸规格圆整即得设计长度ls，所选的ls应等于或大于并最接近lj，取ls=90 mm。

GMM 棒半径rt须满足对最大输出力Fmax的要求:

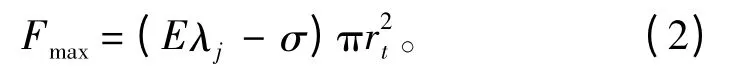
式中:E 为弹性模量;σ 为预压应力。

由于GMA 的设计指标为最大输出位移Fmax=2 400 N;GMM 棒的弹性模量E = 30 GPa。为了使GMM 棒工作在线性区域，取预压应力σ=8.1 MPa，此时设计半径为:

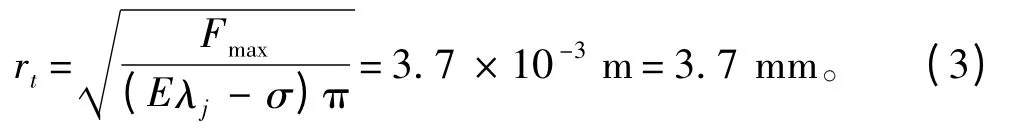
由于受加工限制以及材料本身工作时的误差影响，取GMM 棒半径rt= 4 mm。

综上所述，GMM 棒的设计长度为ls= 90 mm，设计半径rt= 4 mm。选择材料时须遵循技术经济性，在保证预定应用场合所需GMA 性能的基础上选择具有最大性价比的材料牌号，本文选取了浙江台州椒光生产的GMM 棒。

2 GMA 磁场有限元仿真

根据课题需要，作动器将工作于恒定磁场或者低频交变磁场环境下，本文将利用Ansys 进行磁场的有限元仿真分析。由于作动器为3D 轴对称结构，故采用2D 轴对称静态磁场分析即可。

2.1 定义各种材料的参数

GMM 棒给定静止相对磁导率ur= 10;线圈、线圈骨架、空气均设置相对磁导率ur= 1;端盖、导磁板和输出杆均设置相对磁导率ur= 5 000。由于本文采用的永磁铁线性度比较好，故采用固定的相对磁导率，经求解ur= 1.099 7。各个部件的材料选择如表1 所示。

表1 作动器的材料性能Tab.1 Material properties of the actuator

2.2 模型的建立与网格划分

在Ansys 绘图区域，建立驱动器的分析模型如图3 所示。选用八节点单元(PLAN53)对模型进行剖分，各节点仅有一个自由度——矢量磁位ZA，注意到在输出杆和壳体之间有0.1 mm 的气隙，这个气隙会产生磁阻，对整个磁路会有一定的影响，必须对它单独建模。为了比较精确的计算出稀土GMM棒在各种电流驱动下的伸缩量，也必须对稀土GMM棒进行单独建模，如图4 所示。整个剖分结果如图5 所示，总计1 109 个单元，3 430 个节点，其中GMM 棒剖分为8 ×30 =240 个单元，气隙剖分为1 ×10 =10 个单元。

2.3 求解过程

图3 驱动器磁场分析几何模型Fig.3 The geometric model of the drive magnetic field analysis

图4 GMM 棒的网格划分Fig.4 The mesh generation of GMM

图5 GMA 有限元模型Fig.5 The finite element model of GMA

首先给线圈平面施加电流密度，根据安培匝数满足NI = 7 308 的条件下，设定N = 1 800，线圈外径为66 mm，内径为16 mm，当激励电流为I = 3 A时，对驱动线圈施加激励载荷J 为:

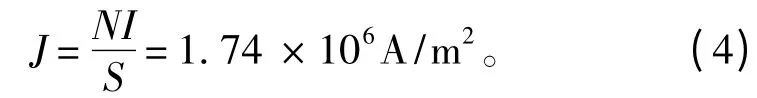
式中:J 为电流密度;N 为线圈匝数;I 为电流大小;S为线圈截面积。

然后根据边界实际情况，需定义平行边界条件或者垂直边界条件。对于平行边界条件，通常都是带有常量AZ 的边界条件，设置AZ = 0 完成对平行边界条件的定义;垂直边界条件会自行发生不需施加任何外部边界条件。

3 GMA 磁场有限元仿真结果分析

3.1 GMA 的外壳材料的选择

GMA 的外壳可以采用磁导率较高的钢制外壳或者采用磁导率较低的铝制外壳。

当采用钢制外壳时，外壳的磁导率较高而GMM棒的磁导率较低，这样永磁铁、导磁板和外壳构成了闭合回路，其仿真结果如图6 所示;当采用铝制外壳时，外壳的磁导率较低(基本为ur= 1，外壳的相对磁导率相当于空气)，这样永磁铁、导磁板、输出杆、GMM 棒、端盖构成闭合回路，其仿真结果如图7 所示。

图6 钢制外壳磁力线分布图Fig.6 The magnetic field lines distribution of steel casing

图7 铝制外壳磁力线分布图Fig. 7 The magnetic field lines distribution of aluminum casing

从图6 可看出，没有磁力线经过GMM 棒，这就意味着在GMM 棒处的磁场强度基本为0，这说明钢制外壳不满足条件，故排除;从图7 可看出，磁场存在磁漏现象，但是经过GMM 棒的磁感线较为密集，这说明GMM 棒附近的磁场强度较大，比钢制外壳有显著提高。故本文选择铝作为GMA 的外壳材料。

3.2 磁场轴线均匀度分析

当通过磁场来驱动材料的时候，一般都希望材料所在的磁场范围均匀，而这均匀性的要求因驱动材料的不同而不同。对于像GMM 棒这样的脆性材料，由于内部磁场的不均匀性会导致内应力的产生从而减少了材料使用寿命，因而实现GMM 棒伸缩规则化的均匀磁场分布，有利于GMA 控制性能的提高，可见均匀的内部磁场非常重要。

在GMA 的闭合磁路中，导磁板、输出杆以及端盖等磁轭材料的相对磁导率对GMM 棒轴线上的磁场均匀度影响较大。对不同相对磁导率的磁轭材料进行仿真分析，分别设定磁轭材料的相对磁导率ur= 1，100，1 000，5 000，然后分别对不同相对磁导率的磁轭材料的GMA 进行建模仿真分析，得出GMM 棒轴线上不同点的磁场强度。

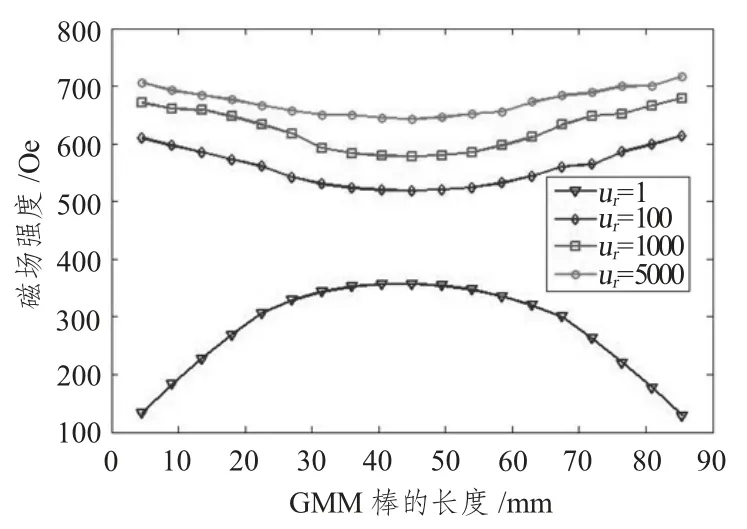
图8 GMM 棒中心线磁场均匀性与磁轭材料相对磁导率的关系Fig.8 The relationship between the field homogeneity of GMM rod center line and the relative magnetic permeability of the yoke material

从图8 可看出，当磁轭材料的相对磁导率ur=1 时，GMM 中部的磁场强度最大，两端磁场强度较小，磁场均匀性很差，这是因为ur= 1 时，磁轭材料不具备约束磁场的作用，无法形成闭合的磁路;当ur≥100 时，磁轭材料具备了约束磁场的作用，随着磁轭材料相对磁导率的增加，GMM 棒中心线的磁场强度在不断的增加，而且其磁场均匀度也逐渐变好。

综上所述，本文选用ur= 5 000 的磁轭材料来形成GMA 的闭合磁路，这时其磁场强度较大，磁场均匀度也较好。对GMA 进行Ansys 仿真分析，其磁场强度分布如图9 所示，从图可看出，在GMM 棒所在区域，其磁场强度较大，满足设计需求。

图9 GMA 的磁场强度分布图Fig.9 The magnetic field strength distribution of GMA

4 结 语

本文通过对GMA 的偏置磁场的选取以及GMM棒的理论计算和选型，提出了GMA 的磁路设计。然后通过GMA 的仿真分析表明:1)当采用圆筒形永磁铁产生偏置磁场时，外壳材料只能选择非导磁材料;2)当GMM 棒在适当的温度、预压力和偏置磁场下工作时，增加磁轭材料的相对磁导率，能够增大其磁场强度，提高驱动磁场的均匀度。

［1］唐鸿洋，张洪平，张羊换，等． 超磁致伸缩合金TbDyFe组织与性能研究现状［J］． 金属功能材料，2013(2):45－51．TANG Hong-yang，ZHANG Hong-ping，ZHANG Yanghuan，et al． Research status of organizational and performance of super-magnetostrictive alloy TbDyFe［J］．Metallic Functional Materials，2013(2):45 －51．

［2］侯淑萍，杨庆新，陈海燕，等．超磁致伸缩材料的特性及其应用［J］．兵器材料科学与工程，2008(5):95 －98．HOU Shu-ping，YANG Qing-xin，CHEN Hai-yan，et al．Characteristic and application of giant magnetostrictive material［J］． Ordnance Material Science and Engineering，2008(5):95 －98．

［3］CORCOLLE R，DANIEL L，BOUILLAULT F． Optimal design of magnetostrictive composites:an analytical approach［J］． Magnetics，IEEE Transactions on，2008，44(1):17 －23．

［4］宣振兴，邬义杰，王慧忠，等．超磁致伸缩材料发展动态与工程应用研究现状［J］．轻工机械，2011(1):116－119．XUAN Zhen-xing，WU Yi-jie，WANG Hui-zhong，et al．Research status of giant magnetostrictive material developments and engineering applications ［J］． Light Indurstry Machinery，2011(1):116 －119．

［5］郭东明，杨兴，贾振元，等．超磁致伸缩执行器在机电工程中的应用研究现状［J］．中国机械工程，2001(6):124－127．GUO Dong-ming，YANG Xing，JIA Zhen-yuan，et al．Research status of giant magnetostrictive actuators in electromechanical engineering ［J］． China Mechanical Engineering，2001(6):124 －127．

［6］王社良，王熙斌，代建波，等．GMA 设计与试验研究［J］．装备制造技术，2010(8):1 －3．WANG She-liang，WANG Xi-bin，DAI Jian-bo，et al．Design and experimental study on giant magnetostrictive actuator［J］． Equipment Manufacturing Technology，2010(8):1－3．

［7］KYUNG H S，SEUNG H C，YOUNG KIM Y． Topology design optimization of a magnetostrictive patch for maximizing elastic wave transduction in waveguides［J］．Magnetics，IEEE Transactions on，2008，44 (10):2373－2380．

［8］GABDULLIN N A，KHAN S H． Application of change in permeability of magnetic shape memory (MSM)alloys for optimization of magnetic circuit in actuators［C］//London，United Kingdom，2014．

［9］赵海涛，何忠波，李中伟．超磁致伸缩驱动器磁路优化设计［J］．兵器材料科学与工程，2008(5):72 －75．ZHAO Hai-tao，HE Zhong-bo，LI Zhong-wei，et al．Magnetic circuit optimum design for giant magnetostrictive actuator［J］． Ordnance Material Science and Engineering，2008(5):72 －75．

［10］李明范，项占琴，吕福在．超磁致伸缩换能器磁路设计及优化［J］．浙江大学学报(工学版)，2006(2):192 －196．LI Ming-fan，XIANG Zhan-qin，LV Fu-zai． Magnet circuit design and optimization of giant magnetostrictive transducer［J］．Journal of Zhejiang University(Engineering Science)，2006(2):192 －196．

［11］谭先涛．超磁致伸缩驱动器的优化设计研究［D］．上海:上海交通大学，2010．TAN Xian-tao． A thesis submitted to shanghai jiao tong university for the degree of master［D］．Shanghai:Shanghai Jiaotong University，2010．