iGPS测量不确定度空间分布分析方法

孙涪龙，赵罡*，王伟，陈磊

(1.北京航空航天大学 机械工程及自动化学院，北京100191;2.上海飞机制造有限公司，上海200436)

iGPS是一种新型数字化大尺寸空间测量设备，相较于其他数字化测量设备，它凭借其大尺寸测量精度高、测量实时性好、可同时多点测量、无光路遮挡失效问题、扩展方便等优势［1-2］，已逐渐在航空航天制造领域得以应用，如美国波音公司将iGPS应用于747，777与787等型号飞机的总装对接中［2-3］，加拿大庞巴迪公司将其用于C系列飞机的装配对接过程等，目前我国的航空航天企业也开始引进iGPS，并对其应用进行了初步探索.

使用iGPS进行实际测量时，为满足测量精度要求，需根据其测量不确定度对测量现场进行快速评估与布局优化，因此对iGPS测量不确定度，尤其是其空间分布规律进行研究具有重要意义.该分布规律与发射器数目与空间布局形式密切相关，不同的发射器的数目与布局方案下测量不确定度空间分布规律差异显著.目前的研究中，文献［4-5］对iGPS角度测量不确定度进行了研究并给出了其变化规律;文献［6］研究了iGPS测量的动态跟踪性能，说明了其在动态测量方面的不足;文献［7］提出了iGPS测量单元与测量网络的概念，对基于单元测量场的iGPS测量网络测量精度进行了分析与仿真，但未涉及发射器不同布局的精度分析;文献［8］研究分析了几种典型发射器布局的iGPS测量精度，但难以推广到任意布局的情况;文献［9］提出了一种基于多不确定度融合的iGPS测量网评价方法，但其建立的两站测量网使用传统的计算方法，且未考虑发射器分布的任意性及其覆盖范围的影响.

本文依据iGPS测量原理，给出了iGPS测量模型，建立了测量不确定度通用两站分析模型，并结合发射器覆盖范围，提出了基于两站模型变换的iGPS测量不确定度空间分布分析方法;通过实验，对比数值仿真结果与实际测量数据，对该方法进行了分析验证.

1 iGPS测量原理

iGPS测量的基本原理为前方交会原理.接收器接收到空间中任意两台发射器的信号，即可解算出测点的空间位置.考虑到发射器空间布局的任意性，建立通用两站测量模型如下.

设两发射器A和B的水平间距为2d，竖直间距为2h.建立如图1所示的坐标系Oxyz，其中，A和B位于平面xOz上，A站的x坐标值与z坐标值小于B站，α为测点M相对于某发射器的方位角，β为测点M相对于某发射器的俯仰角.

图1 通用两站测量模型Fig.1 Universal two-station measurement model

计算测点 M 的坐标(x，y，z).由于 x，y 与 z均可从A与B两方面出发进行计算，而传统的前方交会计算方法［10］未完全考虑两方面情况.本文对每个坐标分量分别引入两个变量，x包括x1与x2两个变量，y与z同理.于是有

当接收器位于多台发射器的覆盖范围内时，系统会对每两台发射器与接收器组成的两站系统进行解算，再经过数据融合得到测点的空间位置坐标.

2 iGPS测量不确定度分析方法

2.1 iGPS测量不确定度

在由n台发射器组成的iGPS测量环境中，空间内一点M(x，y，z)的测量不确定度定义为

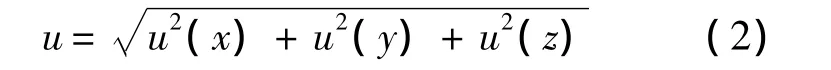
设测点相对于发射器i的方位角为αi、俯仰角为 βi，其不确定度分别为 u(αi)与 u(βi)，则

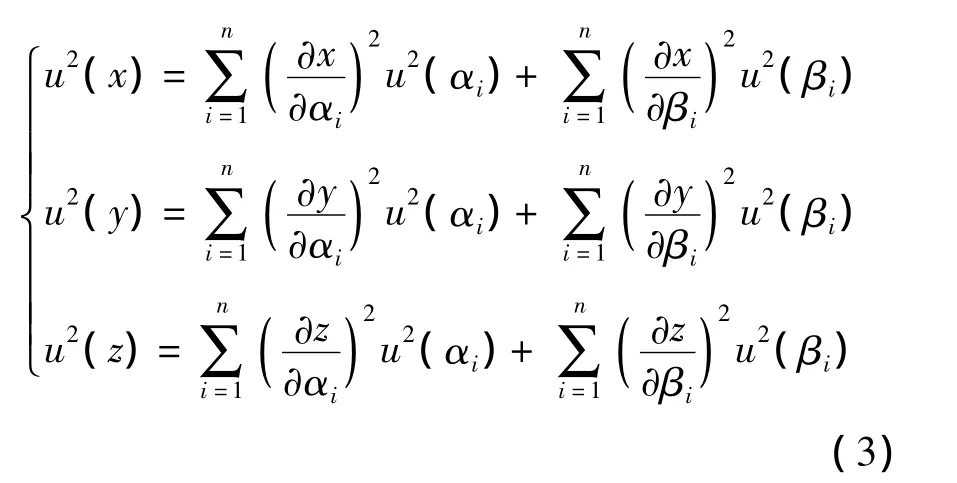
据此，本文首先在通用两站测量模型的基础上，建立iGPS测量不确定度通用两站分析模型.

2.2 不确定度通用两站分析模型

根据式(3)计算测量不确定度.对式(1)求导，可得

由式(3)可计算得到u(x1)与u(x2)，u(y1)与u(y2)以及u(z1)与u(z2).

式(1)中，由于每个坐标分量均包括两个信息，为了将各坐标分量包含的两个信息进行统一，需要进行数据融合.

数据融合的方法包括加权平均法、卡尔曼滤波法、贝叶斯估计法等［11］.其中，加权平均法简单、直观，尤其适用于对原始数据进行直接处理的情形［12］，因此本文采用加权平均法对各坐标信息进行融合.

使用加权平均法进行数据融合应保证融合后数据的标准差最小，并据此确定各原始数据的权因子［13-14］.据此，n个数据的融合结果q的标准差其中，σi为各原始数据的标准差，ωi为对应的权因子.由多元函数求极限理论，可解得 σq有最小值此时 ωi=采用该方法进行数据融合后，结果的标准差小于任一源数据的标准差［14］.

据此对 x，y与 z坐标进行数据融合.由于u(x1)=u(x2)，u(y1)=u(y2)，故有

由于 u(z1)≠u(z2)，令 σ1=u(z1)，σ2=u(z2)，则可求出 ω1与 ω2，并有

进一步，根据式(2)可计算合成不确定度u.可以看出，由于两发射器位于xOz平面上，因此u关于xOz平面对称分布.

关于 u(αA)，u(αB)，u(βA)与 u(βB)的取值，英国巴斯大学与英国国家物理实验室的研究表明［4］，iGPS发射器与接收器引起的测角标准不确定度平均值约为:方位角 0.80″，俯仰角0.25″，即

至此，建立了测量不确定度通用两站分析模型.该模型考虑了分别由两站出发的计算结果，并通过数据融合进行统一，提高了完备性;考虑了两发射器在水平方向与竖直方向的分布，可对任意布局的两站系统进行分析.

2.3 基于两站模型变换的测量不确定度空间分布分析方法

在一个由多台发射器组成的iGPS测量系统中，任取两台发射器A和B可组成一个两站系统并确定测点T的坐标.为计算T在该两站系统中的测量不确定度，需要对上述两站模型进行变换.

如图2所示，设两发射器A和B在全局坐标系Oxyz下的坐标值为(xA，yA，zA)和(xB，yB，zB)，其中将z坐标值较小的发射器设定为A站，即满足zA＜zB，测点T 的坐标值为(xT，yT，zT).由A 和B 两发射器的全局坐标，计算其水平间距和竖直间距，建立通用两站模型坐标系 O′x′y′z′;利用几何关系计算测点 T 在两站模型中的坐标 T′(x′T，y′T，z′T)，有

图2 两站模型变换示意图Fig.2 Two-station model transformation

对y′T的符号进行判断，根据上述两站模型的对称性可知，由于不确定度u关于xOz平面对称分布，于是可取对 x′T的符号进行判断，由于在两站模型中，两发射器的x坐标值互为相反数，因此根据TA与TB在xOy平面上的投影即可判断 x′T的符号，即:若，则

将两发射器水平与竖直间距以及T′坐标值(x′T，y′T，z′T)代入两站模型，计算得到测点 T 在该两站系统中的测量不确定度.

对于一个由n台发射器组成的iGPS测量系统，可计算得到C2n个基本测量信息与不确定度信息［15］.使用加权平均法对这些基本坐标信息进行数据融合，根据各基本坐标信息的不确定度计算权因子与总不确定度，并进一步计算得到测点的融合坐标.

上述即为iGPS测量不确定度空间分布分析方法.由于考虑了发射器数目与空间布局因素，该方法可对任意iGPS测量环境的测量不确定度空间分布规律进行计算分析.

2.4 考虑发射器覆盖范围的影响

由于每个iGPS发射器发出的激光扇面在方位方向的覆盖角度范围为360°，而在俯仰方向的覆盖角度范围为±30°，因此需考虑发射器覆盖范围的影响.在一个两站系统中，只要接收器在某一个发射器的激光覆盖范围之外，则不能解算出测点的坐标信息.

据此对建立的测量不确定度空间分布分析方法进行修正，在进行测量不确定度计算之前，首先判断接收器是否在各个发射器的覆盖范围之内，剔除不能照射到接收器的发射器，仅保留有效的发射器参与解算.

3 数值仿真与实验分析

3.1 方案设计

3.1.1 实验环境

实验场地长15 m，宽6 m，高3 m，地基稳定，震动较小，密闭与遮光条件良好，可保证环境温度与湿度基本恒定，墙壁与地面反射系数小，实验区域无阳光或人工光源直射.

3.1.2 实验设备

Nikon iGPS 4Tx全空间跟踪定位测量系统，Leica AT901-B激光跟踪仪.其不确度变如表1所示.

表1 实验设备测量不确定度比较Table1 Measurement uncertainty comparison of experimental equipment

在设定的实验空间范围内，该激光跟踪仪的测量不确定度小于0.05mm，而iGPS测量不确定度为0.25mm，激光跟踪仪的测量精度为iGPS的5倍以上.因此，可以使用激光跟踪仪作为测量基准设备.

3.1.3 实验方案

针对设定的实验环境，进行测量不确定度的数值仿真计算与实际测量偏差的对比分析.将上述不确定度空间分布分析方法编程实现，计算测量不确定度空间分布数值仿真结果;使用激光跟踪仪与iGPS对空间内选定的测量点进行测量，并对两者的测量结果进行偏差计算.对比数值仿真结果与实测偏差结果，对该方法进行验证.

为验证建立的测量不确定度通用两站分析模型，本文构建两站系统作为研究对象;在使用iGPS进行实际测量时，考虑到测量精度、覆盖范围、光线遮挡等方面的因素，一般均以配置4台发射器的四站系统作为实际测量的最小系统，因此为验证提出的iGPS测量不确定度空间分布分析方法，本文构建四站系统作为研究对象，进行数值仿真计算与实际测量偏差的对比分析.

3.2 两站系统

3.2.1 实验方法与过程

在实验场地内建立iGPS两站系统并标定，得到发射器的位置坐标，如表2所示.

表2 两站系统发射器布局位置坐标Table2 Transmitter coordinates of two stations measurement

选定z坐标为0 mm的平面为分析平面，在5 m×6m的范围进行数值仿真计算与实际偏差测量.将两发射器的水平与竖直距离输入仿真计算程序，算得该两站系统在选定采点平面上的测量不确定度分布规律;实际选取50个点，每个点分别使用iGPS与激光跟踪仪测量5次，计算每个测量点的两测量仪器测量值偏差，得到实测偏差分布.

3.2.2 结果与分析

该两站系统在选定的采点平面上的测量不确定度分布数值仿真结果如图3所示.

根据实测结果，计算得到各个测量点的偏差分布如图4所示，其中箭头指向为偏差方向.

由数值仿真结果可以看出，在两站系统中，两发射器连线及附近区域的测量不确定度明显大于周围区域，可达到0.2 mm以上.这是因为在此区域内，测量点与两发射器形成的夹角很大，根据前方交会原理，随着该夹角向180°靠近，测点空间不确定度显著增大.根据实际测量结果，在此区域内的3个测量点的测量偏差值均大于0.5 mm，显著大于其他测量点的测量偏差.

排除两发射器的连线区域，在靠近两发射器的近似椭圆区域内测量不确定度较小，可达到0.05 mm，并随测量点与两发射器距离的增大而增大.若两站水平距离为d，则在水平方向上d×d的范围内，测量不确定度可达0.2mm以内.从实测结果来看，在此范围内的30个测量点中，有25个点的测量偏差小于0.2mm，偏差均值为0.13mm.

分别计算方位方向(x和y方向)上与俯仰方向(z方向)上的测量不确定度，其分布规律如图5所示.

根据数值仿真结果，方位方向的测量不确定度空间分布和数值均与总不确定度相近，而俯仰方向均在0.03mm以内;实测偏差结果表明，各点的测量偏差多集中在方位方向，均值为0.15 mm，俯仰方向的分量均值为0.04 mm.

图3 两站系统测量不确定度分布数值仿真Fig.3 Numerical simulation of two stations measurement uncertainty distribution

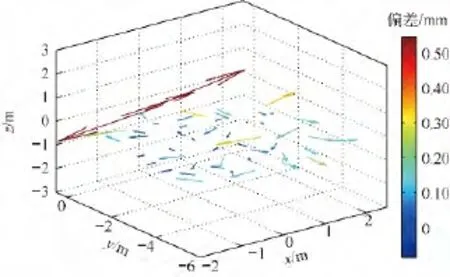
图4 两站系统实际测量偏差分布Fig.4 Actual deviations distribution of two stations measurement

图5 两站系统方位方向与俯仰方向测量不确定度分布数值仿真Fig.5 Numerical simulation of two stations measurement uncertainty distribution in azimuth and elevation direction

3.3 四站系统

3.3.1 实验方法与过程

在实验场地中建立iGPS四站系统.为反映iGPS发射器空间布局的任意性，4台发射器的布局形式为:在水平方向上为略狭长近似梯形的四边形，在竖直方向上错开.对系统标定得到发射器的位置坐标，如表3所示.

表3 四站系统发射器布局位置坐标Table3 Transmitter coordinates of four stations measurement

根据现场环境，选定z坐标为－713 mm的平面为分析平面，在12 m×6 m的范围进行数值仿真计算与实际偏差测量.将标定所得4台发射器位置坐标输入仿真计算程序，算得该四站系统在选定采点平面上的测量不确定度分布规律;实际选取90个点，每个点分别使用iGPS与激光跟踪仪测量5次，计算每个测量点的两测量仪器测量值偏差，得到实测偏差分布.

3.3.2 结果与分析

该四站系统在选定的采点平面上的测量不确定度分布数值仿真结果如图6、图7所示.

根据实测结果，计算得到各个测量点的偏差分布如图8所示.

图6 四站系统测量不确定度分布数值仿真Fig.6 Numerical simulation of four stations measurement uncertainty distribution

图7 四站系统测量不确定度分布数值仿真(俯视图)Fig.7 Numerical simulation of four stations measurement uncertainty distribution(top view)

图8 四站系统实际测量偏差分布(俯视图)Fig.8 Actual deviations distribution of four stations measurement(top view)

由数值仿真结果可以看出，测量不确定度在靠近各个发射器的区域有明显的跳变增大，其数值介于0.12～0.20 mm之间，且该区域呈圆形/扇形分布.这是由于iGPS发射器发出的激光扇面在俯仰方向的覆盖角度范围为±30°，而在该区域内，接收器超出了该发射器的覆盖范围，故不能获得测点相对于该发射器的角度信息.因此在临近发射器位置的测量不确定度增大，实际上是由于有效发射器数目减少引起的.由实测偏差数据，这一区域内测量点的测量偏差均大于0.15 mm，均值为0.18 mm.

本实验中，4台发射器的布局相对狭长，根据数值仿真结果，测量空间中间区域的测量不确定度相对较大，约为0.10 mm，两侧区域的测量不确定度较小，均小于0.08 mm.实测结果中，排除临近各发射器的区域，中间区域的30个测量点的偏差均值为0.13 mm，两侧区域的49个测量点的偏差均值为0.10 mm.

由于环境因素的影响，实测偏差略大于数值仿真结果.从仿真结果来看，除发射器附近区域，测量空间的不确定度均在0.12 mm以内;根据实测偏差结果，排除发射器附近区域的测量偏差均小于0.2 mm，均值为0.11 mm.

4 结论

本文提出了一种iGPS测量不确定度空间分布分析方法.给出了iGPS测量模型，建立了测量不确定度通用两站分析模型.在此基础上，进一步提出了测量不确定度空间分布分析方法，并根据发射器覆盖范围对其进行了修正.

数值仿真结果与实测偏差对比结果表明，两站系统与四站系统的仿真数据结果与实测偏差结果吻合良好，提出的iGPS测量不确定度空间分布分析方法能较好地对测量不确定度空间分布规律进行描述.使用该方法，可对发射器为任意数目与空间布局的iGPS测量环境的测量不确定度空间分布规律进行计算分析.

该测量不确定度空间分布分析方法可用于iGPS测量环境的测量精度快速计算与分析评估，并可为测量现场的发射器布局方案优化提供依据.

References)

［1］ 邹方，尚可.未来工厂的数字化测量世界［J］.航空制造技术，2008(19):26-29.Zou F，Shang K.Digital measurement world for future factory［J］.Aeronautical Manufacturing Technology，2008(19):26-29(in Chinese).

［2］ 郭洪杰，王碧玲，赵建国，等.iGPS测量系统实现关键技术及应用［J］.航空制造技术，2012(11):46-49.Guo H J，Wang B L，Zhao J G，et al.Key technology and application of iGPS measuring system［J］.Aeronautical Manufacturing Technology，2012(11):46-49(in Chinese).

［3］ 于勇，陶剑，范玉青，等.波音787飞机装配技术及其装配过程［J］.航空制造技术，2009(14):42-47.Yu Y，Tao J，Fan Y Q，et al.Assembly technology and process of Boeing 787 jet［J］.Aeronautical Manufacturing Technology，2009(14):42-47(in Chinese).

［4］ Muelaner J E，Wang Z，Jamshidi J，et al.Study of the uncertainty of angle measurement for a rotary-laser automatic theodolite(RLAT)［J］.Proceedings of the Institution of Mechanical Engineers，Part B:Journal of Engineering Manufacture，2009，223(3):217-229.

［5］ Muelaner J E，Wang Z，Martin O，et al.Verification of the indoor GPS system，by comparison with calibrated coordinates and by angular reference［J］.Journal of Intelligent Manufacturing，2012，23(6):2323-2331.

［6］ Wang Z，Mastrogiacomo L，Franceschini F，et al.Experimental comparison of dynamic tracking performance of iGPS and laser tracker［J］.The International Journal of Advanced Manufacturing Technology，2011，56(1-4):205-213.

［7］ 杜福洲，陈哲涵，唐晓青.iGPS测量场精度分析及其应用研究［J］.航空学报，2012，33(9):1737-1745.Du F Z，Chen Z H，Tang X Q.Precision analysis of iGPS measurement field and its application［J］.Acta Aeronautica et Astronautica Sinica，2012，33(9):1737-1745(in Chinese).

［8］ Schmitt R，Nisch S，Schonberg A，et al.Performance evaluation of iGPS for industrial applications［C］//Indoor Positioning and Indoor Navigation(IPIN)，2010 International Conference on.Zurich:IEEE，2010:1-8.

［9］ 李洋，周自力，马骊群，等.基于多不确定度融合的室内GPS测量网评价方法［J］.计量学报，2012，33(z1):24-27.Li Y，Zhou Z L，Ma L Q，et al.The evaluation method for the indoor GPS measurement network based on multi-uncertainty fusion algorithm［J］.Acta Metrologica Sinica，2012，33(z1):24-27(in Chinese).

［10］ 龙华伟，翟超.空间前方交会法及其在测试技术中的应用［J］.计测技术，2005，25(6):51-54.Long H W，Zhai C.The principle of spatial forward intersection and discussion about its applications［J］.Metrology ＆ Measurement Technology，2005，25(6):51-54(in Chinese).

［11］ 吴秋轩，曹广益.多传感器信息融合方法综述［J］.机器人，2003，25(z1):741-745.Wu Q X，Cao G Y.A survey of multisensor information fusion algorithm［J］.Robot，2003，25(z1):741-745(in Chinese).

［12］ 王会清，韩艳玲.基于多传感器与数据融合技术的研究［J］.计算机与现代化，2002(9):64-67.Wang H Q，Han Y L.The study of the technology based on multisensor and data fusion［J］.Computer and Modernization，2002(9):64-67(in Chinese).

［13］ 凌林本，李滋刚，陈超英，等.多传感器数据融合时权的最优分配原则［J］.中国惯性技术学报，2000，8(2):36-39.Ling L B，Li Z G，Chen C Y，et al.Optimal weight distribution principle used in the fusion of multi-sensor data［J］.Journal of Chinese Inertial Technology，2000，8(2):36-39(in Chinese).

［14］ 王炯琦，周海银，吴翊.基于最优估计的数据融合理论［J］.应用数学，2007，20(2):392-399.Wang J Q，Zhou H Y，Wu Y.The theory of data fusion based on state optimal estimation［J］.Mathematica Applicata，2007，20(2):392-399(in Chinese).

［15］ 朱永国，黄翔，秦龙刚.基于局域GPS的飞机惯性导航部件安装校准［J］.南京航空航天大学学报，2009，41(5):615-619.Zhu Y G，Huang X，Qin L G.Installation and calibration of airplane inertial navigation based on indoor GPS［J］.Journal of Nanjing University of Aeronautics and Astronautics，2009，41(5):615-619(in Chinese).