空气耦合超声检测中脉冲压缩方法的参数选优

周正干，马保全，孙志明，周晖，黄姿禹，刘晶晶

(1.北京航空航天大学 机械工程及自动化学院，北京100191;2.上海飞机制造有限公司航空制造技术研究所，上海200436)

空气耦合超声检测技术是一种以空气作为耦合介质的非接触声学检测方法，被认为是检测与评价纤维增强复合材料(即 CFRP，GFRP，GLARE)、蜂窝夹芯/泡沫夹芯结构材料、金属、耐温陶瓷材料等质量的有效手段［1-3］.空气耦合条件下，由于空气同检测对象之间巨大的声阻抗差及空气对高频声波的高吸收率，造成接收信号微弱且信噪比低，提高空气耦合条件下接收信号强度及信噪比是该技术发展及应用所面临的首要问题.雷达系统中，为了提高检测范围及距离分辨率，基于相关运算的脉冲压缩技术实现了从大时宽、低幅值信号向小时宽、高幅值信号的转换，有效解决了雷达距离分辨率与平均功率之间的矛盾.因此，具有诸多优异特性的脉冲压缩技术为空气耦合超声信号信噪比的提高提供了有效的参考手段，基于该技术建立的空气耦合超声检测方法能显著提高信号的鲁棒性及检测图像的分辨率，并已应用到医学超声领域［4］.国外针对脉冲压缩方法应用于超声无损检测领域的研究开展较深入［5］，目前常用的脉冲压缩处理方法包括频率调制脉冲压缩技术和相位调制脉冲压缩技术.频率调制脉冲压缩技术已经在超声无损检测领域获得应用(线性调频、非线性调频等)［6-8］，尤其在医学高精度超声成像方面得到验证［4，9］.相位编码脉冲压缩方法也是雷达信号处理的重要手段，相比频率调制脉冲压缩方法而言，相位编码信号的调制更便捷，更容易获得高主副比(主瓣旁瓣幅值比)的脉冲压缩信号，因此该技术也已得到普遍重视和广泛应用，并逐步向超声检测领域推广［10］.

在特殊复合材料的空气耦合超声检测方面，应用脉冲压缩技术可使接收信号信噪比得到大幅提高，上述方法已被认为是可行、可靠的信号处理手段，已成为空气耦合超声检测技术的重要研究内容之一.与脉冲压缩方法在雷达信号处理技术中的成熟应用不同，空气耦合超声检测中超声换能器激发出的超声波信号与雷达信号有较大差异，针对脉冲压缩参数的调整对超声信号脉冲压缩效果的影响并不十分明确，影响了该技术在空气耦合超声检测领域的推广应用.为更好地利用脉冲压缩方法来提高空气耦合超声信号信噪比，研究脉冲压缩方法的参数选优问题很有必要.

本文基于脉冲压缩技术的基本原理及其在超声检测领域的实现过程，建立完善的空气耦合超声检测系统(并编制上位机C++算法实现超声信号的实时脉冲压缩处理).针对窄带空气耦合超声换能器分别就线性调频、非线性调频及相位编码脉冲压缩方法的关键参数(激励信号时宽、带宽、巴克码位数及载波周期数)对脉冲压缩效果(主瓣峰值及信噪比)的影响开展实验研究，进而获得脉冲压缩参数的选取准则.最后，以模拟缺陷的蜂窝夹芯复合材料试样为对象，验证参数选优后的脉冲压缩方法在空气耦合超声检测中的实际应用效果.

1 基本理论

1.1 脉冲压缩处理技术原理及其实现

所谓脉冲压缩，就是采用宽脉冲发射以提高发射的平均功率，在接收时采用匹配滤波器进行脉冲压缩以获得窄脉冲信号，进而提高检测能力的同时又不失距离分辨力［11］.发射脉冲宽度t与压缩后系统有效脉冲宽度t0的比值，称为脉冲压缩比，即

因为脉冲压缩后的有效脉冲宽度t0=1/B(B为调制信号带宽)，所以上式可写成:

即脉冲压缩比等于信号的时宽带宽积.

匹配滤波器的作用是处理系统通过匹配滤波过程对输入的信号进行一次相关运算.在输入为已知信号及白噪声时，所得输出信噪比最大的线性滤波器就是匹配滤波器.假设参考信号为us(t)，与参考信号相关的接收信号为xs(t)，对接收信号进行脉冲压缩处理过程如图1所示.基于相关性原理，两相关信号的脉冲压缩过程实际上是接收信号xs(t)与参考信号的匹配滤波器进行卷积运算，其中匹配滤波器的频率特性函数实际上是参考信号频谱的共轭.为提高数据处理效率，实现信号的实时处理，卷积运算一般通过频域点乘来实现，经傅里叶逆变换获得时域脉冲压缩信号.

图1 接收信号的脉冲压缩原理Fig.1 Pulse compression principle of received signal

基于上述原理，对超声信号进行脉冲压缩的实现过程主要分为以下几个步骤:

1)编制合理的激励信号来激发超声换能器，同时对激励信号进行快速傅里叶变换(FFT)，存储变换后的数据作为参考信号;

2)基于参考信号获得匹配滤波器的频率响应函数(即对激励信号频域上的各点取共轭);

3)对超声接收信号采样点进行快速傅里叶变换，并与匹配滤波器频率响应函数在频域点乘;

4)将点乘后的数据进行傅里叶逆变换(IFFT)，获得脉冲压缩后的时域信号.

1.2 三大脉冲压缩处理技术

1.2.1 线性调频脉冲压缩技术

线性调频(LFM)是超声信号脉冲压缩中的常用调制手段.线性调频信号激励超声发射换能器，通过匹配滤波器(matched filter)对接收到的透射信号进行压缩处理，可得到满足要求的检测信号［12］.LFM信号(也称Chirp信号)的数学表达式为［7］

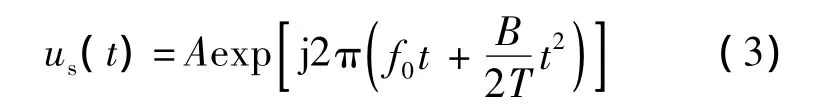
式中，A为信号幅值;f0为基频(选择换能器中心频率);T为调制信号时宽.线性调频信号斜率K为

当选定调制信号时宽T，调制信号带宽B，则调制信号瞬时频率以斜率K做线性变化.在超声检测中，一般需要调整时宽T和带宽B来获得最佳的脉冲压缩效果.

1.2.2 非线性调频脉冲压缩技术

由于线性调频方法产生的激励信号瞬时频率呈线性增加，信号频带与换能器频带相符程度不高.非线性调频(NLFM)信号是线性调频信号的一种改进，使调制后信号频带与换能器频带接近，从而能使换能器在各个频段都能输出最高的能量，大大提高了脉冲压缩信号主副比［8］.NLFM信号是按特定的信号幅度谱来生成，假设以相角函数表示的非线性调制信号为

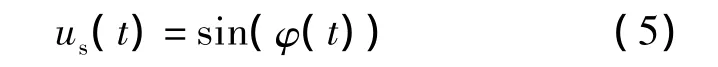
式中φ(t)为相角函数.根据相位逗留原理，求得激励超声换能器的非线性调频信号us(t)为

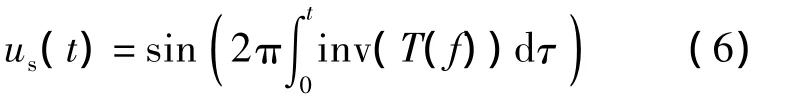
其中T(f)为群延时函数，表达式为

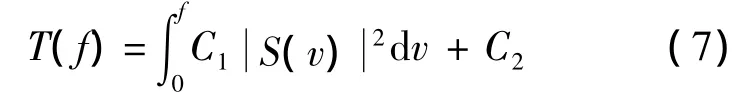
式中S(v)为调制信号幅度谱，通过对超声换能器扫频获得.根据设定的调制时宽T确定边界条件T(f1)=0，T(f2)=T，可得常数项 C1，C2.

将非线性调频脉冲压缩技术应用于超声检测时，由于换能器频谱分布特性已知，只要设置不同调制时宽T，即可获得一系列不同的激励信号.

1.2.3 相位编码脉冲压缩技术

常用的相位编码方式有巴克码、互补格莱(Golay)码、M 序列、Taylor码、弗兰克码等.选择相位编码的依据是其自相关函数旁瓣幅值足够小，使主副比尽可能小.二相巴克码信号具有良好的自相关特性及噪声抑制特性，被认为是一种获得最小时域旁瓣的有效编码方式［13-14］.二相编码信号的复包络可表示为

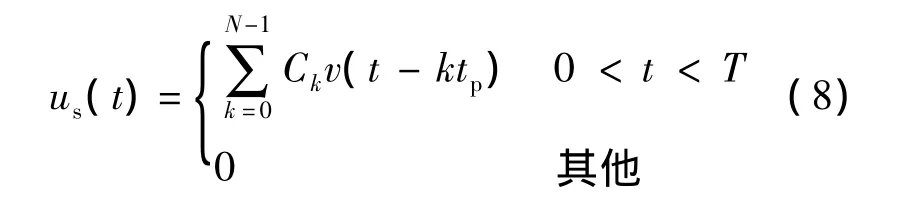
式中，v(t)为子脉冲函数;tp为子脉冲宽度;N为子脉冲个数;T=N·tp为二相编码信号持续时间.相位编码调制信号是离散伪随机信号，二相编码信号的频谱函数主要是由子脉冲函数的频谱决定，其带宽近似等于子脉冲的带宽［15］，即B=1/tp，因此时宽带宽积 D=T·B=N，当改变时宽(或带宽)时，带宽(或时宽)相应发生变化，时宽带宽积D仅与子脉冲个数N有关.常规二相巴克码有2，3，4，5，7，11，13 位等(如表1 所示).

表1 不同码长的巴克码序列及其主副比Table1 Different length Barker code sequence and the corresponding main to side lobe ratio

2 实验分析

2.1 穿透式空气耦合超声检测原理及实验系统

实验采用的空气耦合超声检测方法为穿透法.穿透法是将两个换能器分别置于被检测试件的两侧，一个探头发射超声波，另一个探头接收透射波，根据超声波穿透试件后的能量变化来判断试件内部质量.空气耦合超声检测系统基本构成如图2所示，包括任意信号发生器、功率放大器、500 kHz空气耦合超声换能器(NCG500-D13)、滤波与前置放大器、含有数据采集卡的上位机，其他还有运动控制系统、扫查架等.

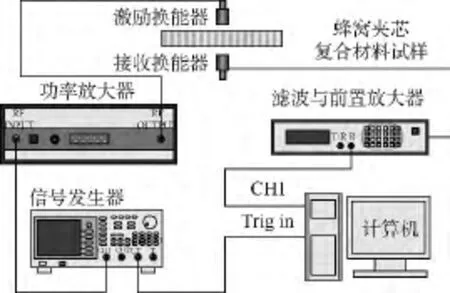
图2 空气耦合超声检测系统基本构成Fig.2 Basic construction of air-coupled ultrasonic testing system

2.2 脉冲压缩方法各参数选优实验

2.2.1 线性调频脉冲压缩

针对线性调频脉冲压缩技术，需要分析不同时宽T、带宽B对超声信号脉冲压缩效果的影响.设置一对空气耦合超声换能器的间距为25 mm，中间无试样，激励电压127 V，增益65.9 dB.

1)时宽的影响.

时宽 T从 10～270 μs每隔20 μs选值一次，获得14种不同时宽脉冲压缩前后的主瓣峰值比，如图3所示.主瓣峰值比随着时宽的增加逐渐增大并且呈近似线性增加.

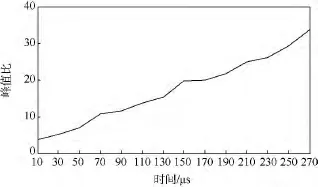
图3 不同时宽条件下线性调频脉冲压缩前后主瓣峰值比Fig.3 Main lobe peak ratio between compressed signal and original signal under different time-width in LFM pulse compression process

2)带宽的影响.

带宽 B 从0.2 ～1.2 MHz每隔 0.2 MHz选值一次，时宽 T分别选取10，70和210 μs，获得3 组定时宽变带宽条件下的脉冲压缩前后主瓣峰值比(如图4所示).采用不同带宽B的激励信号激励换能器，脉冲压缩前后主瓣峰值比随带宽增加逐渐减小，最后趋于稳定.

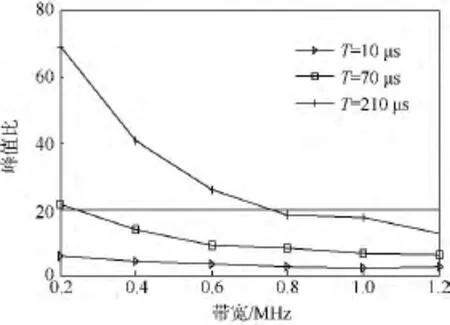
图4 不同带宽条件下线性调频脉冲压缩前后的主瓣峰值比Fig.4 Main lobe peak ratio between compressed signal and original signal under different band-width in LFM pulse compression process

2.2.2 非线性调频脉冲压缩技术

非线性调频脉冲压缩中，由于换能器频谱分布特性已知，时宽T是唯一能改变的参数.为分析时宽T对脉冲压缩效果的影响，设置激励电压为67 V，信号增益为 55.9 dB.时宽 T从 10～270 μs每隔20μs选值一次，获得不同时宽条件下的脉冲压缩前后主瓣峰值比，如图5所示.

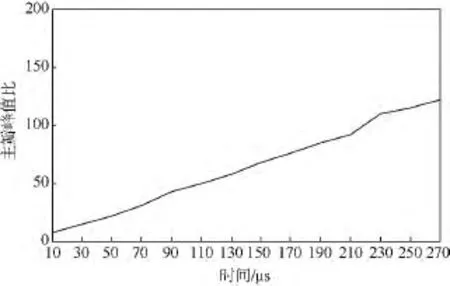
图5 不同时宽条件下非线性调频脉冲压缩前后的主瓣峰值比Fig.5 Main lobe peak ratio between compressed signal and original signal under different time-width in NLFM pulse compression process

脉冲压缩前后主瓣峰值比随着时宽T的增加呈近似线性增长，因此，在选择非线性调频脉冲压缩参数时，应尽可能选择大时宽的调制信号.

2.2.3 相位编码脉冲压缩技术

1)不同位数巴克码序列的脉冲压缩效果.

保持上述实验条件不变，采用码元为正弦的巴克码序列(码长分别为2，3，4，5，7，11，13)激励换能器，对各自接收的回波信号进行脉冲压缩处理，得到脉冲压缩前后主瓣峰值的变化如图6所示.

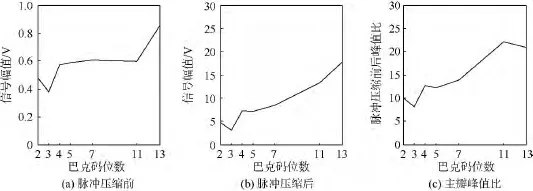
图6 不同位数巴克码序列脉冲压缩前后主瓣峰值Fig.6 Main lobe peak of pulse compressed signal with different length Barker code and unprocessed signal

由图6可知，脉冲压缩前，接收信号主瓣峰值随巴克码位数的增加呈类阶梯状增大，经匹配滤波之后，输出信号主瓣峰值以及脉冲压缩前后主瓣峰值比也随着巴克码位数的增加逐渐增大，当巴克码序列位数为13时，主瓣峰值达到最大.

2)不同周期13位巴克码的脉冲压缩效果.

采用1～6个周期载波巴克码信号激励换能器(以2 周期为例，其序列 Ck={1，1，1，1，1，1，1，1，1，1，－1，－1，－1，－1，1，1，1，1，－1，－1，1，1，－1，－1，1，1}，其他周期编码方式以此类推)，获得不同周期数的13位巴克码序列的脉冲压缩效果如图7所示.

图7 不同周期13位巴克码脉冲压缩前后主瓣幅值变化Fig.7 Main lobe peak ratio between compressed signal with different cycle 13 bit Barker code and original signal

由图7可知，载波周期增大时脉冲压缩信号主峰值不断提高，1～3周期获得的脉冲压缩信号主峰值从17.79 V变为102.2 V.而随着载波周期数的不断增大，主瓣和旁瓣开始变得难以分辨.因此，采用多周期载波13位巴克码信号作为超声激励信号时，可尽量选择多个周期载波信号，但同时要兼顾信号主副比，保证脉冲压缩后的超声透射信号易于识别，使其满足C扫描检测要求.

2.3 有试样时脉冲压缩方法的检测性能对比

2.3.1 试样准备

在一块无缺陷的碳纤维蒙皮-铝蜂窝夹芯复合材料表面，按从大到小的顺序分别粘接不同的厚纸片以模拟蜂窝夹芯材料中的缺陷.试样尺寸及缺陷布置如图8所示，蜂窝试样光学照片如图9所示(蜂窝芯厚12 mm，蒙皮厚1 mm).

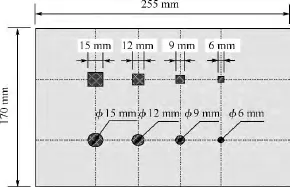
图8 试样尺寸及缺陷布置Fig.8 Specimen size and defect allocation

图9 蜂窝夹芯复合材料试样照片Fig.9 Photograph of honeycomb composite sample

2.3.2 透射信号能量及信噪比对比

根据上述结果可知，线性调频脉冲压缩参数选取应遵循大时宽、小带宽的原则;非线性调频脉冲压缩参数仅由时宽决定，应选择尽量大的时宽;相位编码脉冲压缩参数在选择13位巴克码且载波周期数为3时可获得良好的脉冲压缩效果.用于对比的3种脉冲压缩参数设置如表2所示.

表2 脉冲压缩性能对比的参数设置Table2 Parameters for comparison experiments of pulse compression efficiency

利用表2中给出的参数对上述3种方法进行有试样条件下的脉冲压缩效果对比.3种方法所用换能器激励电压均为 200 V，增益均为103.9 dB.脉冲压缩处理前，接收信号中的透射始波几乎全被噪声淹没，采用不同脉冲压缩方法后的信号如图10～图12所示，从各图中都能识别透射始波.

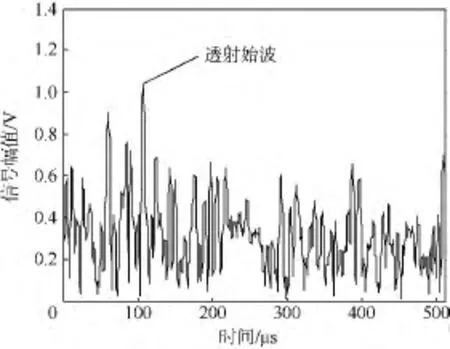
图10 线性调频脉冲压缩后的信号Fig.10 Pulse compressed signal with linear frequency modulation method

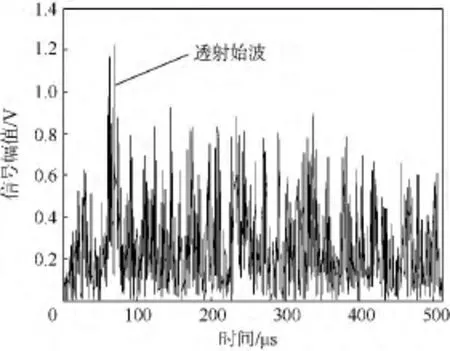
图11 非线性调频脉冲压缩后的信号Fig.11 Pulse compressed signal with non-linear frequency modulation method

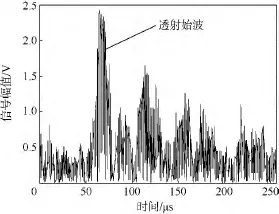
图12 相位编码脉冲压缩后的信号Fig.12 Pulse compressed signal with phase code modulation method

脉冲压缩后的透射超声信号信噪比如表3所示.由表3可知，相位编码脉冲压缩信号信噪比明显优于线性调频和非线性调频脉冲压缩方法的信噪比.

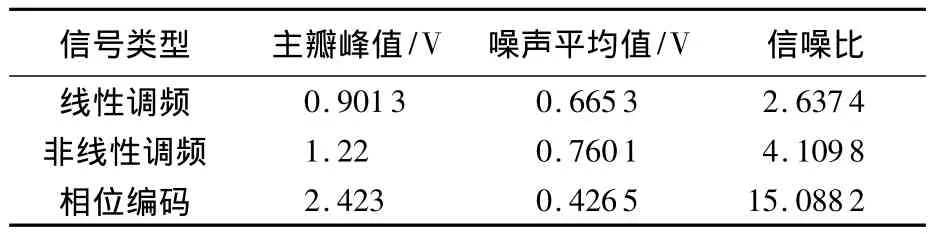
表3 脉冲压缩后的透射超声信号信噪比(SNR)Table3 Signal to noise ratio(SNR)comparison of pulse compressed signal of through-transmitted ultrasound

2.3.3 蜂窝夹芯试样的C扫描检测

按照表2中的参数对不同脉压处理后的透射始波设置闸门进行 C扫描检测，成像对比如图13～图15所示.由图13～图15可知，相位编码脉冲压缩方法获得的C扫描图中对缺陷及蜂窝芯格的识别能力明显优于线性调频和非线性调频脉冲压缩方法的识别能力.

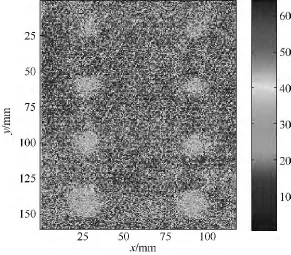
图13 线性调频脉冲压缩C扫描成像结果Fig.13 C-scan result based on linear frequency modulation pulse compression process

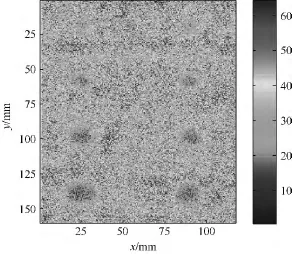
图14 非线性调频脉冲压缩C扫描成像结果Fig.14 C-scan result based on non-linear frequency modulation pulse compression process

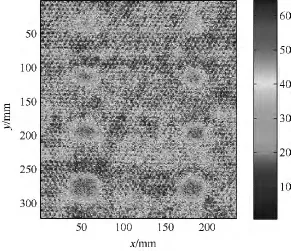
图15 相位编码脉冲压缩C扫描成像结果Fig.15 C-scan result based on phase code modulation pulse compression process

3 结论

1)针对窄带空气耦合超声换能器，线性调频脉冲压缩方法中激励信号的设计应遵循大时宽、小带宽的原则;非线性调频脉冲压缩效果仅由时宽决定，应选择尽量大的时宽，但激励信号时宽不能太大以防止损坏超声换能器;相位编码脉冲压缩方法中选择13位巴克码时获得优良的脉冲压缩效果.随着巴克码载波周期数的增大，脉冲压缩主瓣峰值不断提高，而对透射信号主瓣的识别能力变差，一般选3周期即可.

2)采用脉冲压缩方法检测高声衰减的复合材料时，在同等激励电压及接收信号增益条件下，相位编码脉冲压缩信号获得最高的透射信号主瓣幅值和信噪比，且获得的C扫描成像效果明显优于线性调频和非线性调频脉冲压缩方法的成像效果.

References)

［1］ Bhardwaj M C，Stead G F.High frequency non-contact ultrasonic analysis of materials:introduction and applications［J］.Nondestructive Evaluation of Materials and Composites V，2001，4336:117-128.

［2］ Imielinska K，Castaings M，Wojtyra R，et al.Air-coupled ultrasonic C-scan technique in impact response testing of carbon fibre and hybrid:glass，carbon and Kevlar/epoxy composites［J］.Journal of Materials Processing Technology，2004，157:513-522.

［3］ Tat H，Georgeson G，Bossi R.Evaluation of air coupled ultrasound for composite aerospace structure［J］.AIP Conference Proceedings，2009，1096(1):912-919.

［4］ Rao N，Mehra S.Medical ultrasound imaging using pulse compression［J］.Electronics Letters，1993，29(8):649-651.

［5］ Pallav P，Hutchins D A，Yin X K.Air-coupled ultrasonic spectroscopy of highly damping materials using pulse compression［J］.IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control，2009，56(6):1207-1217.

［6］ Lam F，Szilard J.Pulse compression techniques in ultrasonic non-destructive testing［J］.Ultrasonics，1976，14(3):111-114.

［7］ 周正干，魏东，向上.线性调频脉冲压缩方法在空气耦合超声检测中的应用研究［J］.机械工程学报，2010，46(18):24-28.Zhou Z G，Wei D，Xiang S.Application of linear-frequency-modulation based pulse compression in air-coupled ultrasonic testing［J］.Chinese Journal of Mechanical Engineering，2010，46(18):24-28(in Chinese).

［8］ 魏东，周正干.改进的非线性调频脉冲压缩方法在空气耦合超声检测中的应用［J］.机械工程学报，2012，48(16):8-13.Wei D，Zhou Z G.Application of non-linear frequency-modulation based pulse compression in air-coupled ultrasonic testing［J］.Journal of Mechanical Engineering，2012，48(16):8-13(in Chinese).

［9］ Laurence R W，Martin D F.Practical spread spectrum pulse compression for ultrasonic tissue imaging［J］.IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control，1998，45(2):349-355.

［10］ Sato R，Shinriki M.Time sidelobe reduction technique for binary phase coded pulse compression［J］.Electronics and Communications in Japan，Part I:Communications(English Translation of Denshi Tsushin Gakkai Ronbunshi)，2001，84(12):52-60.

［11］ 蔡凤丽.相位编码信号脉冲压缩旁瓣抑制技术研究［D］.南京:南京理工大学，2009.Cai F L.Research on side-lobe suppression for phase encoding signal［D］.Nanjing:Nanjing University of Science and Technology，2009(in Chinese).

［12］ Gan T H，Hutchins D A，Billson D R，et al.The use of broadband acoustic transducers and pulse-compression techniques for air-coupled ultrasonic imaging［J］.Ultrasonics，2001，39(3):181-194.

［13］ Chen W H，Deng J L.Ultrasonic non-destructive testing using barker code pulse compression techniques［J］.Ultrasonics，1988，26(1):23-26.

［14］ Sun G M，Liu G S，Gu H.Signal analysis and processing for random binary phase coded pulse radar［J］.Journal of Systems Engineering and Electronics，2004，15(4):520-524.

［15］ 周谊珉.雷达信号分析技术与软件设计［D］.南京:南京大学，2012.Zhou Y M.Radar signal analysis technology and software design［D］.Nanjing:Nanjing University，2012(in Ch inese).