基于Riccati方程解的高增益未知输入观测器设计

朱芳来，张永军

(同济大学 电子与信息工程学院，上海200092)

从20世纪70年代开始，未知输入观测器设计一直是现代控制研究领域所关注的热点之一.未知输入观测器(UIO)不仅被广泛地应用到控制系统中，同时在故障诊断和基于混沌同步的保密通讯［1］等领域也有着重要的应用.发展至今，未知输入观测器设计无论是针对线性系统还是非线性系统，都已经有众多的研究成果呈现［2-3］.早期，未知输入观测器设计着重于如何绕开未知输入的影响而达到状态估计的目的［4］，之后未知输入与状态一并估计的方法［5］得到了重视.

未知输入和测量噪声并存，在实际的控制系统中普遍存在.因而，对同时具有测量噪声和未知输入的系统进行所谓的未知输入观测器设计，更具有挑战性，成为近期学者们所关注的研究热点之一［6］.例如，文献［7］采用了降维观测器设计方法，通过选取恰当的降维观测器增益，有效处理了一类具有未知输入和测量噪声的线性系统的状态和噪声估计及未知输入重构问题.Bejarano等处理了具有相同未知输入和测量噪声的一类强可检测的奇异线性系统的观测器设计、未知输入重构及噪声估计，并讨论系统强可观和检测的充要条件［8］.描述系统，也称之为奇异系统，经常被用来描述工程系统、社会系统和经济系统等实际系统［9-10］.由于描述系统在处理具有输出测量噪声的系统时，可以方便地把输出噪声当作描述系统的扩展状态，因而该方法在观测器设计中被广泛使用［11-13］.例如，文献［8］针对具有相同未知输入和测量噪声的非线性系统结合描述系统方法提出了全维观测器设计方法.文献［14］结合描述系统、滑模理论和自适应控制的方法，针对一类非线性系统提出了一种系统状态和噪声同时估计的自适应鲁棒观测器，该方法同样实现了对未知输入的重构.文献［15］提出了一种鲁棒H∞滑模描述观测器，对具有未知输入或者输出干扰的不确定系统提出了状态估计及未知输入重构方法.

从上面对具有输出测量噪声和未知输入观测器的研究动态分析可以看出，把输出测量噪声看作描述系统的扩展状态已经成为十分有效的方法.在描述系统的基础上如何进一步地设计具有鲁棒性的观测器，具有重大研究意义.本文尝试在描述系统的基础上，利用通过求解Riccati方程的方法，构造观测器增益矩阵，以此提出估计一类Lipschitz非线性系统的状态和测量噪声的方法，同时还考虑了对未知输入重构的问题.

1 问题描述

考虑如下具有未知输入和测量噪声的非线性系统:

其中，x∈Rn，y∈Rp，u∈Rm分别为系统的状态、可测输出和已知控制输入;η∈Rr为未知输入;ω∈Rw为测量噪声;A∈Rn×n，B∈Rn×s，D∈Rn×r，C∈Rp×n和 E∈Rp×w为已知矩阵.假设系统(A，C)可观，矩阵B，D和E都是列满秩的，C是行满秩的，并且满足 rank［B D］=s+r.

假设1 非线性项函数 f(x，u)∈Rs满足Lipschitz条件，即存在一个Lipschitz常数γ使得

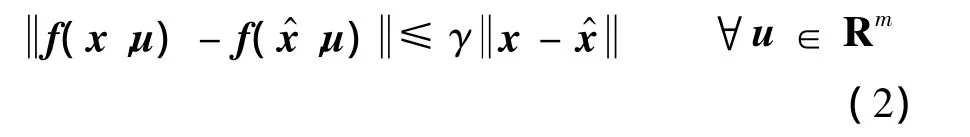
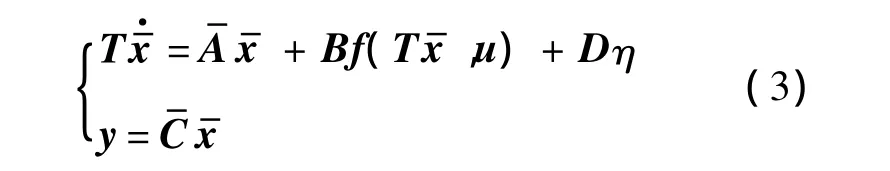
2 观测器设计

对于描述系统(3)，考虑如下观测器:

其中，ζ∈Rn+w为观测器状态;∈Rn+w为扩展状态 估 计;N ∈ R(n+w)×(n+w)，L ∈ R(n+w)×p，G ∈R(n+w)×n和 F∈R(n+w)×p为需要设计的矩阵.

引理1 存在矩阵G和F满足:

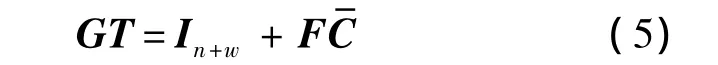
证明 式(5)可以写为XR=In+w，其中

而

由于矩阵E是列满秩，所以R是列满秩的，这意味着RTR可逆，因而R的右逆R+=(RTR)－1RT存在，且R+R=In+w.

取X=R+－Y(In+p－RR+)，则它为 XR=In+w的解，其中 Y∈Rn×(n+p)可以取为任意矩阵.当计算出X后，就可以得到

证毕

现定义扩展状态估计误差为

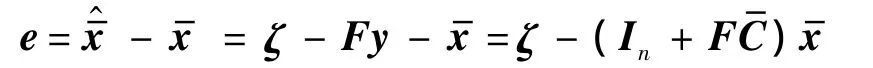
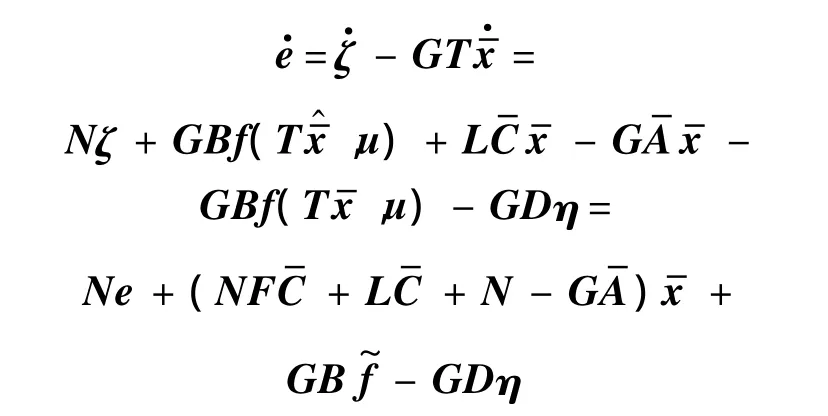
即

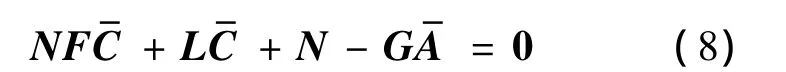
并再记M=－GD∈Rn×r，则误差方程就可化为

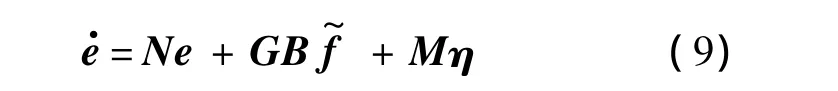
有关代数方程(8)，有如下的引理.

引理2 对任意的矩阵K∈R(n+w)×p，如下定义的矩阵:

满足式(8).

证明 直接代入式(8)验证即可.

对于满足式(8)的任意解N和L，至少存在一个矩阵K∈R(n+w)×p使得N和L可以分别有式(10)和式(11)的形式.事实上，K=(L+NF)就是一个满足要求的K.

由前面的讨论知道，对任意的矩阵Y和K，由式(6)、式(10)和式(11)所确定的矩阵 G，F，N和L可以使观测器误差方程具有式(9)的形式.本文试图确定矩阵K，使得误差方程(9)具有任意小邻域收敛意义下的零平衡状态，即使得系统(4)是系统(3)的观测器.

进一步地，观测器误差方程(9)可以等价地写为

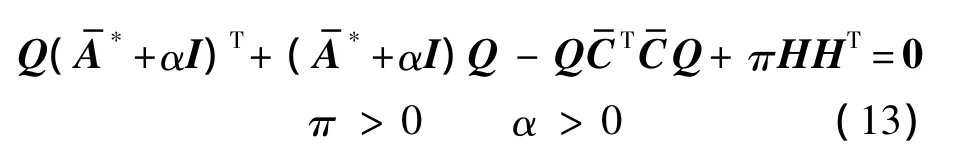
引理 3［18-19］假设系统(+ αI，H，)是最小项系统，，H 满秩，并且 rank()=rank(H)，那么 Riccati方程(13)的解Q(π)满足

定理1 在引理3同样的前提条件下，则Riccati方程(13)有正定解，这时只要取 K=Q，则系统(4)是系统(3)任意小邻域收敛意义下的观测器.

证明 考虑Lyapunov函数V(t)=eTQ－1e，则它沿着误差方程(9)的微分是

由于

由式(13)得到

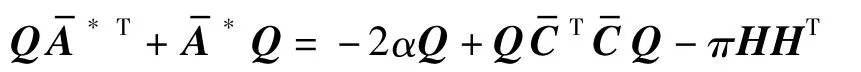
上式代入式(14)得到

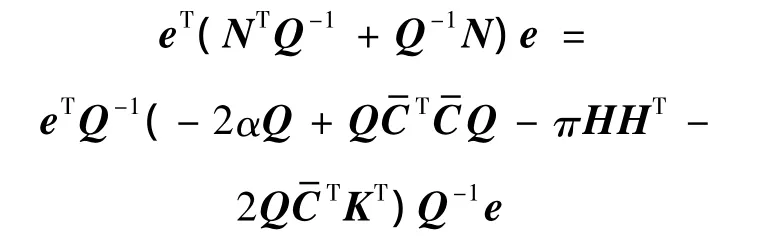
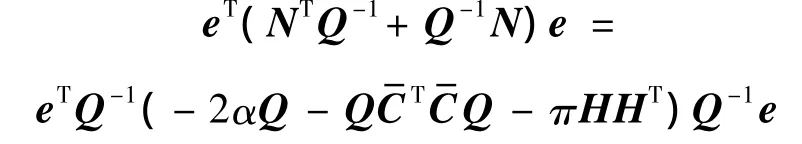
即

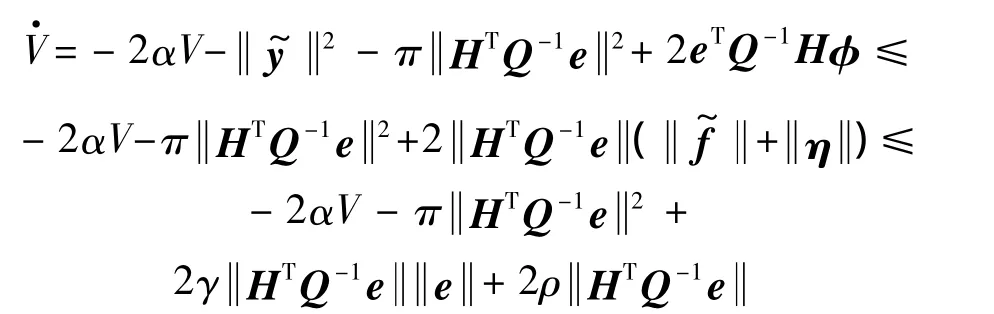
对于任意的a＞0，有

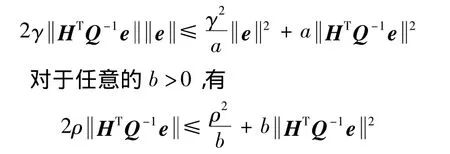
于是，得到

只要取充分大的π，上式就说明，误差e在充分小的邻域内收敛到零.

证毕

在得到了扩展状态的估计后，可以由如下的方式得到原系统状态和测量噪声的估计分别如下:

上述证明验证了Riccati方程求解矩阵K的有效性，结合引理1和引理2，观测器设计算法步骤如下.

步骤1 按式(6)求出矩阵G和F;

步骤2 取充分大的正数α和π，求解代数Riccati方程(13)，得到正定矩阵解Q，并根据K=Q计算出 K;

步骤3 将K的值代入式(10)和式(11)分别得到矩阵N和L.

3 未知输入重构

本节在状态得到估计的前提下，提出一种未知输入代数重构方法.该方法能对未知输入的最小二乘最优解进行任意领域收敛估计.同时，为了在重构中避免可测输出微分信息的使用，本文还基于他人的前期研究，考虑了一种二阶高增益滑模观测器，用于估计可测输出的微分.

由系统(3)，在等式两边同时左乘矩阵G得

将式(5)代入式(16)，化简得

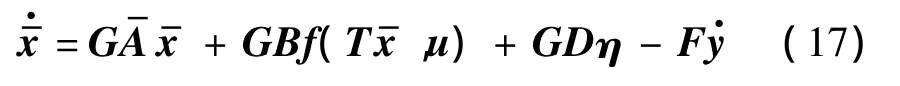
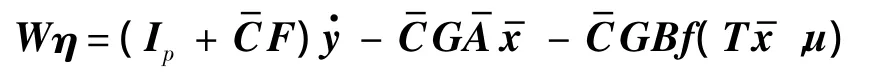
可知未知输入的最小二乘最优解为

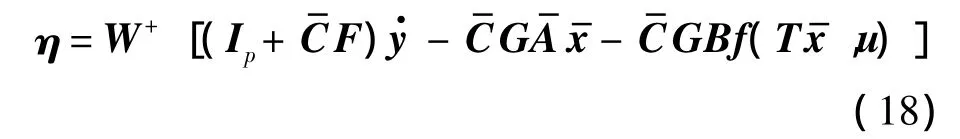
其中 W+=(WTW)－1WT.

由式(18)可知，为了重构未知输入的最小二乘最优解，必须事先知道可测输出的微分.为此，本文引入二阶高增益滑模观测器对输出的微分进行估计.

由式(17)知

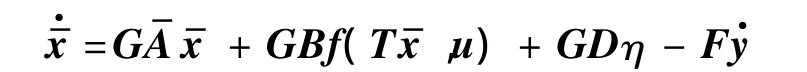
令

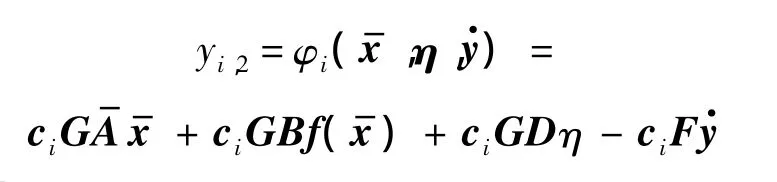
则有

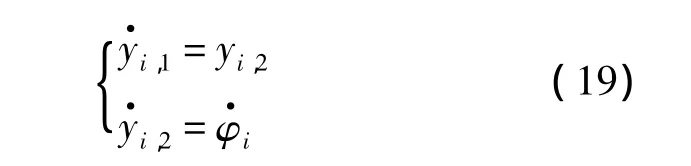
基于Levant［20］的工作，可以引入二阶高增益滑模观测器获取原系统的输出微分估计.

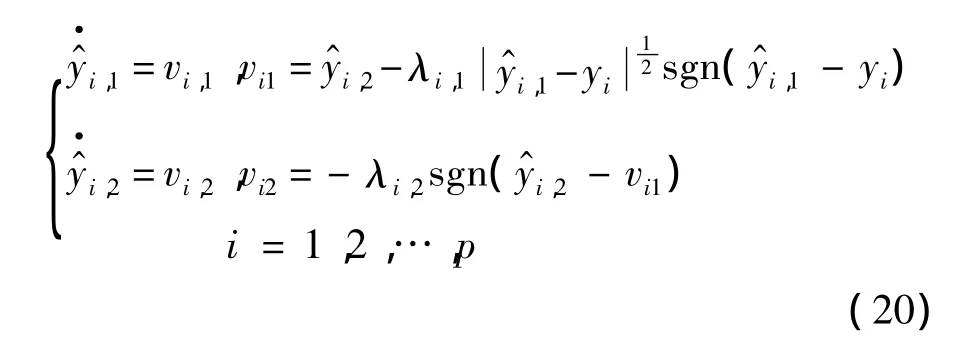
定理2［20］在未知输入有界的条件下，如下二阶系统:是式(19)的高阶滑模观测器，该观测器不仅精确地估计出yi，而且在有限时间内能精确估计yi的微分.具体而言和 ξ =是输出y及的精确估计.其中 λi，1和 λi，2是需要合理选取的观测增益.

基于观测器(4)所给出的扩展状态估计和式(20)所提供的系统输出微分的估计，提出能对未知输入最小二乘最优解式(18)进行重构的方法如下:

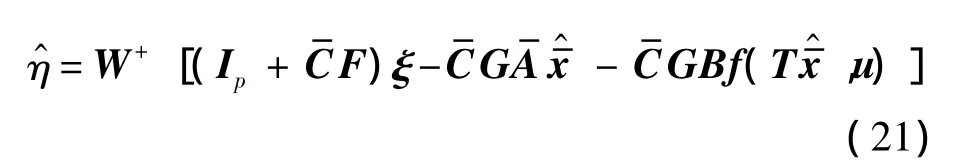
4 仿真分析

考虑单连杆柔性关节机器人模型作为仿真对象，描述成系统(1)的形式:

非线性项 f(x，u)=1.3sin x1+u，未知输入项η(t)=2.5sin(3t+1)，输出测量噪声ω(t)=15cos(10t+3).假设初始的状态x1(0)=x2(0)=x3(0)=x4(0)=1，初始的状态估计，噪声初始估计值(0)=2．

根据式(6)可以计算出G和F，限于篇幅，具体值没有给出.取正数α=0.05和π=109，通过式(13)可以求得Q，然后计算出:

又由式(10)和式(11)，可以计算出N和L，限于篇幅，略去具体值的给出.计算出相应的矩阵值之后，就可以根据式(4)构造能够同时对状态和测量噪声估计的观测器.状态估计效果由图1～图4给出，而测量噪声的重构效果由图5提供.从图1～图5可以看出，无论是状态估计，还是测量噪声的重构，效果令人满意.

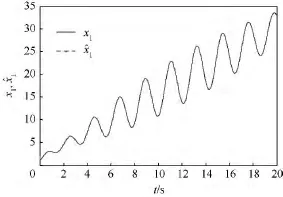
图1 状态(t)对x1(t)的跟踪Fig.1 Track of(t)to x1(t)

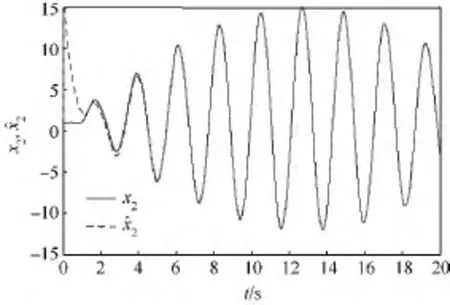
图2 状态(t)对x2(t)的跟踪Fig.2 Track of(t)to x2(t)

图3 状态(t)对x3(t)的跟踪Fig.3 Track of(t)to x3(t)

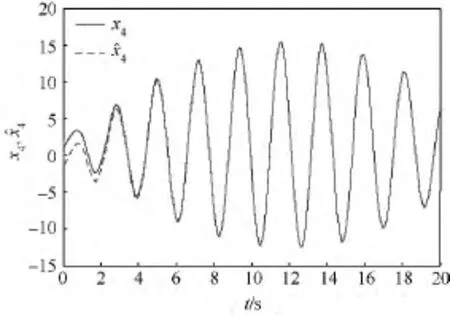
图4 状态(t)对x4(t)的跟踪Fig.4 Track of(t)to x4(t)

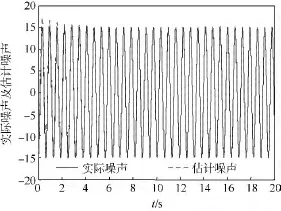
图5 估计噪声及实际噪声Fig.5 Estimation of noise and the actual noise

为了重构未知输入，必须知道原系统有限时间内的输出微分估计，这可由二阶高增益滑模观测器(20)给出.图6分别给出了的估计误差.图7给出了未知输入重构效果.

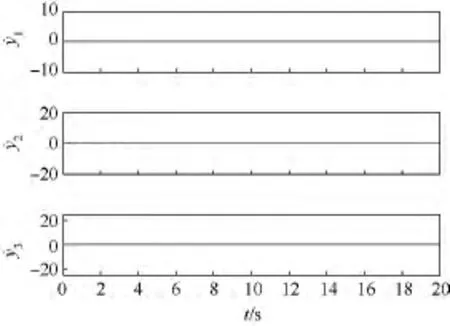
图6 输出微分的估计误差Fig.6 Estimation error of the output differential

图7 未知输入及其重构Fig.7 Unknown input and its reconstruction

5 结论

本文综合研究具有未知输入和噪声的一类非线性系统，经试验验证表明:

1)提出了状态估计和未知输入和测量噪声同时重构的方法.

2)本文的方法可以有效地抵消系统未知输入项给观测器带来的影响，即在不知道未知输入的情况下，实现对系统状态任意小邻域收敛估计.

3)本文还结合二阶高增益滑模观测器，提出了一种未知输入代数重构方法，且方法具有不必用到系统可测输出微分信息的优点.

References)

［1］ Boutayeb M，Darouach M，Rafaralahy H.Generalized state-space observers for chaotic synchronization and secure communication［J］.IEEE Transactions on Circuits System-I:Fundamental Theory and Applicatins，2002，49(3):345-349.

［2］ Wang S H，Davison E J，Dorato P.Observing the states of systems with unmeasurable disturbance［J］.IEEE Transactions on Automatic Control，1975，AC-20:716-717.

［3］ Kudva P，Viswanadham N，Ramakrishna A.Observers for linear systems with unknown inputs［J］.IEEE Transactions on Automatic Control，1980，AC-25:113-115.

［4］ Yang F Y，Wilde R W.Observer for linear systems with unknown inputs［J］.IEEE Transactions on Automatic Control，1988，33(7):677-681.

［5］ Zhu F L.State estimation and unknown input reconstruction via both reduced-order and high-order sliding mode observers［J］.Journal of Process Control，2012，22(1):296-302.

［6］ Bejarano F J，Floquet T，Perruquetti W，et al.Observability and detectability of singular linear systems with unknown inputs［J］.Automatica，2013，49(3):793-800.

［7］ Yang J Q，Zhu F L，Sun X.State estimation and simultaneous unknown input and measurement noise reconstruction based on associated observers［J］.International Journal of Adaptive Control and Signal Processing，2013，27(10):846-858.

［8］ Bejarano F J，Floquet T，Perruquetti W，et al.Observability and detectability of singular linear systems with unknown inputs［J］.Automatica，2013，49(3):793-800.

［9］ Duan G R.Analysis and design of descriptor linear system［M］.New York:Spring-Verlag New York Inc，2010.

［10］ Sentouh C，Mammar S，Glaser S.Simultaneous vehicle state and road attributes estimation suing unknown input proportional-integral observer［C］//IEEE Intelligent Vehicles Symposium Eindhoven.New York:IEEE，2008:690-696.

［11］ Wang Z，Shen Y，Zhang X，et al.Observer design for discretetime descriptor systems:an LMI approach［J］.System ＆ Control Letters，2012，61(6):683-687.

［12］ Darouach M.On the functional observers for linear descriptor systems［J］.Systems ＆ Control Letters，2012，61(3):427-434.

［13］ Koenig D.Observer design for unknown input nonlinear descriptor systems via convex optimization［J］.IEEE Transactions on Automatic Control，2006，51(6):1047-1052.

［14］ Dimassi H，Loria A，Belghith S.Continuously-implement sliding-mode adaptive unknown-input observer under noisy measurements［J］.Systems ＆ Control Letters，2012，16:1194-1202.

［15］ Lee D J，Park Y，Park Y-S.Robust H∞sliding mode descriptor observer for fault and discrete time descriptor system［J］.IEEE Transactions on Automatic Control，2012，57(12):2928-2012.

［16］ Saberi A，Sannuti P，Chen B M.H2Optimal control［M］.Englewood Cliffs，NJ:Prentice-Hall，1995，57(11):145-168.

［17］ Lewis F L.Applied optimal control and estimation［M］.Englewood Cliffs，NJ:Prentice-Hall，1992:176-184.

［18］ Doyle J C，Stein G.Robustness with observers［J］.IEEE Transations on Automatic Control，1979，AC-24:607-611.

［19］ Kwakernaak H，Sivan R.Linear optimal control systems［M］.New York:Wiley，1972:193-198

［20］ Levant A.High-order sliding modes:differentiation and outputfeedback control［J］.International Journal of Control，2003，76(9-10):924-941.