基于广义线性模型的固体推进剂贮存寿命评估

洪东跑，王英华，管飞，马小兵

(1.中国运载火箭技术研究院，北京100076;2.北京航空航天大学 可靠性与系统工程学院，北京100191)

固体推进剂是影响发动机贮存寿命与可靠性的主要因素，对固体推进剂的贮存寿命与可靠性进行评估具有重要的意义.传统的寿命与可靠性评估通常是基于产品的失效或寿命终态特征进行的，而随着产品设计、制造水平的提高以及新技术、新材料与新工艺的不断应用，固体推进剂正逐步朝着高可靠、长寿命的方向发展.固体推进剂在允许的时间和成本内难以通过发动机解剖、试车和实弹试射等试验来获得有效的寿命与可靠性数据［1］.因此，传统的寿命与可靠性评估方法难以满足固体推进剂的贮存评估要求.然而，在贮存过程中，固体推进剂的外观性能、燃烧性能、力学性能、密度等会随着贮存时间发生变化［2］.针对固体推进剂的这一特性，国内外学者致力于研究固体推进剂的非破坏性评估方法［1-4］，这类方法通过固体推进剂老化机理研究其性能随贮存时间的变化规律，从而对其贮存寿命与可靠性进行评估.

固体发动机及固体推进剂平贮件贮存试验均表明固体推进剂的力学性能会随贮存时间不断退化.退化是能够引起产品性能发生变化的一种物理或化学过程，这一变化随着贮存时间逐渐发展［5］.当退化量超出规定的阈值时，会导致推进剂失效.通过定期对固体推进剂平贮件的力学性能进行检测，可获得其在贮存过程中的力学性能退化数据.通过对退化数据进行建模分析，描述产品的性能随贮存时间的变化规律，并外推确定产品的失效时间，可在产品失效数据少甚至无失效的情况下，实现对高可靠、长寿命产品的贮存寿命与可靠性评估［6-9］.

本文结合固体推进剂在贮存过程中的失效模式和失效机理，通过研究固体推进剂的力学性能在贮存过程中随贮存时间的变化规律，给出了一种利用性能退化数据的固体推进剂贮存寿命与可靠性评估方法.

1 固体推进剂性能退化

固体推进剂在贮存过程中失效主要是由其贮存环境的影响和内在因素的变化造成的.在贮存过程中，固体推进剂的性能包括力学性能、燃烧性能和密度等会发生退化，并最终导致推进剂失效，其中力学性能的退化主要表现为推进剂抗拉强度下降.在推进剂浇铸成型后，在固化过程中抗拉强度会有一个明显上升过程，稳定后，随着贮存时间缓慢开始下降.抗拉强度下降属于正常老化现象，通常是由于推进剂黏合剂分子结构网络链条断裂，使聚合物分子离解，变为更小的单元，增加了推进剂的流动性，降低了强度［2］.

为了获得固体推进剂力学性能退化数据，需要在贮存过程中对推进剂的力学性能进行测试.为了便于对固体推进剂进行性能测试且不破坏固体发动机结构，在实际应用中，通常将推进剂方坯作为平贮件与固体发动机一起贮存.通过对方坯进行性能测试以反映固体推进剂的性能随贮存时间的变化情况.有研究表明受固化条件、贮存条件、应力状态条件等因素影响，方坯预测寿命与发动机推进剂实际寿命之间存在一定差异，但其在贮存过程中失效模式和失效机理是一致的，同时大多数性能参数变化趋势也是相同的［10］.鉴于推进剂的长寿命要求，利用方坯预测寿命的偏差在工程应用可接受范围.因此，在国内外工程应用中，通常利用方坯来分析推进剂的贮存性能，同时会采取相应的措施，减少方坯和发动机推进剂贮存相关性能的差异性.

本文选取抗拉强度作为固体推进剂性能研究对象，通过研究其随贮存时间的变化规律，对固体推进剂的贮存寿命进行分析.取n个固体推进剂方坯作为平贮件与固体发动机一起贮存，在贮存过程中，随机选取固体推进剂方坯进行力学性能试验，以测试固体推进剂贮存后的抗拉强度.由于该试验为破坏性试验，故每个方坯只能进行一次试验.根据试验的顺序对n个固体推进剂方坯的退化数据进行排序:

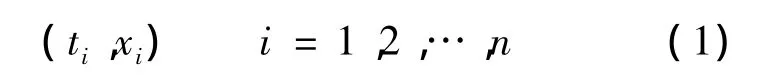
其中ti和xi分别为第i个方坯的贮存时间和抗拉强度.

2 利用退化数据的可靠性建模

在寿命与可靠性分析中，位置-刻度模型是一种常用的可靠性模型.它已普遍应用于电子元器件、机械产品的疲劳、金属材料断裂及材料老化等寿命试验中［11］.利用位置-刻度模型来描述固体推进剂抗拉强度随贮存时间的变化规律.记抗拉强度变量为X，则位置-刻度模型为

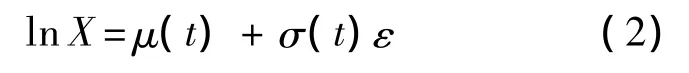
其中，μ(t)和σ(t)为位置参数和刻度参数;ε为分布函数为G(x)的随机变量，其中G(x)与位置参数及刻度参数无关.对式(2)进行变换可得

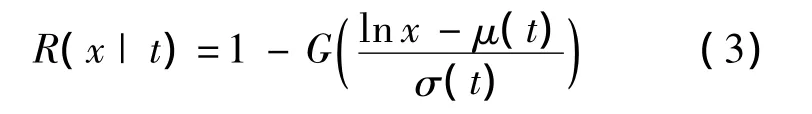
在贮存过程中，固体推进剂的抗拉强度会不断退化，即位置参数μ(t)是关于贮存时间t的函数.在工程应用中，通常利用变换线性模型来描述固体推进剂的性能与贮存时间的关系:

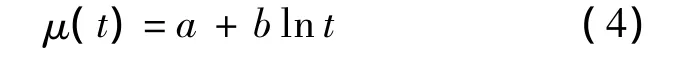
其中a，b为待估参数.

由于固体推进剂的生产工艺较为稳定，不同推进剂方坯抗拉强度的一致性较好，而且刻度参数受贮存时间影响较小，可假设σ(t)为常数，记为σ.则式(2)的位置-刻度模型可变换为

3 基于广义线性模型的可靠性评估

3.1 参数估计

利用式(5)位置-刻度模型来描述固体推进剂抗拉强度与贮存时间的关系，假设ε的分布函数G(x)已知，记其密度函数为g(x).对于式(1)的退化数据，令Y=ln X，yi=ln xi，则Y的密度函数为则样本 y1，y2，…，yn对应的似然函数为

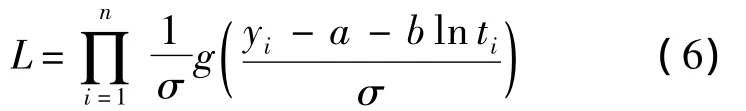
利用数值求解方法，由式(6)可得模型未知参数的极大似然估计.为了增强对退化数据的适应性并改善参数估计效率.利用广义线性模型求解未知参数的极大似然估计.

假设固体推进剂抗拉强度X服从双参数Weibull分布，则Y服从标准极值分布，其分布函数为G(x)=1－exp(－ex)，密度函数为g(x)=exp(－ex)ex，记 wi=exp((yi－a－b ln ti)/σ)，代入式(6)可得对数似然函数

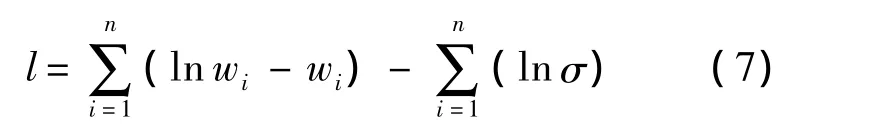
当σ已知时，可以利用Poisson分布广义线性模型来获得参数a和b的极大似然估计［11-13］.

由式(7)的对数似然函数对σ求导有

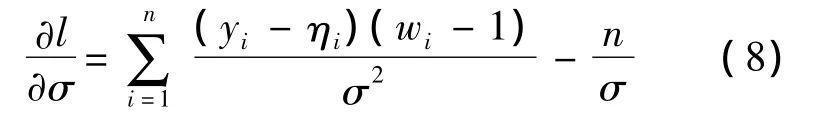
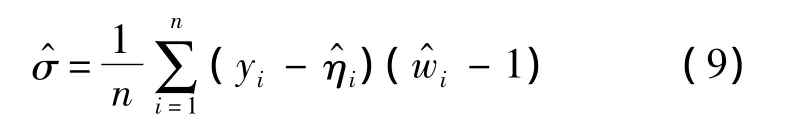
如此循环迭代直到参数估计没有显著变化［14］，可得参数估计和

3.2 贮存寿命与可靠性评估

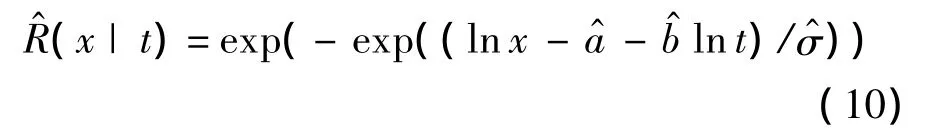
给定贮存可靠度R，由(10)可得固体推进剂的贮存寿命估计:

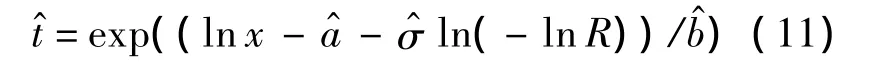
在工程应用中，通常还需要获得寿命与可靠度置信下限.令 θ =(a，b，σ)T，由 Wald 统计量可知，极大似然估计具有渐近正态性:

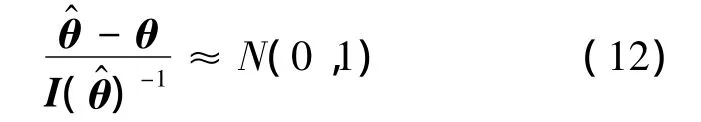
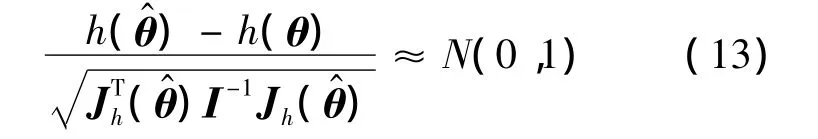
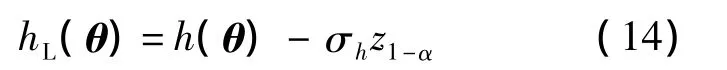
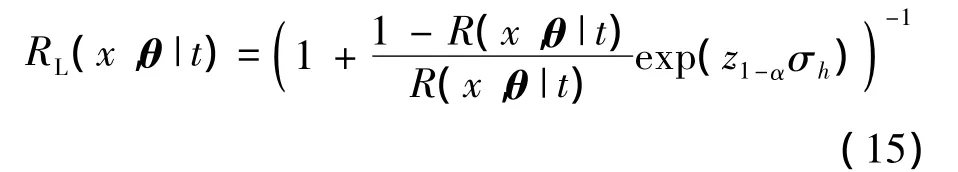
同理，结合贮存寿命与可靠度之间的单调关系，由式(15)通过迭代可得贮存寿命置信下限tL.

4 数值算例

为研究固体推进剂在贮存过程中的性能变化规律，制作了3个固体推进剂方坯进行贮存，并对方坯进行力学性能试验，如表1所示.该型固体推进剂的极限抗拉强度为0.55 MPa.

表1 固体推进剂方坯抗拉强度Table1 Tensile strength of solid propellant carton

为了验证本文给出方法的合理性与可行性，假设固体推进剂的抗拉强度服从双参数Weibull分布，在表1的数据基础上，利用数值模拟方法，随机产生一组数据如表2所示.

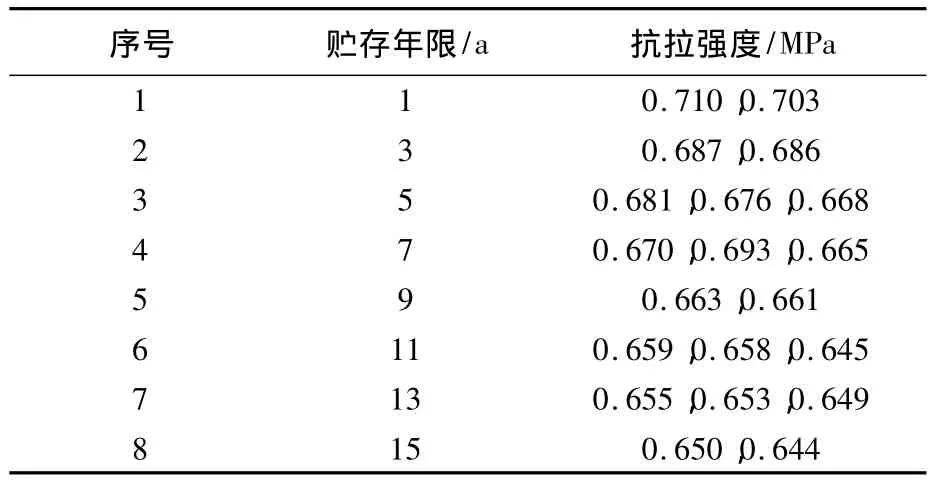
表2 固体推进剂数值模拟数据Table2 Simulation data of solid propellant

利用表2的固体推进剂数值模拟数据，可得参数的极大似然估计= －0.3382= －0.0320，=0.023 7.给定置信水平 γ =0.9，由式(15)分别可得固体推进剂在15a和20a的贮存可靠性下限0.995 7和0.994 1，同时可得固体推进剂贮存可靠度为0.995的贮存寿命置信下限17.2 a.

5 结论

1)利用位置-刻度模型来描述固体推进剂抗拉强度随贮存时间的变化规律，为度量推进剂性能随贮存时间的变化提供了一种可行的方法.

2)利用广义线性模型，对贮存寿命模型系数估计进行整体统计推断，有效地增强了对性能数据的适应性，提高了贮存寿命与可靠性评估精度.

References)

［1］ 张昊，庞爱民，彭松.固体推进剂贮存寿命非破坏性评估方法-老化特征参数监测法［J］.固体火箭技术，2005，28(4):271-275.Zhang H，Pang A M，Peng S.Nondestructive assessment approaches to storage life of solid propellants(I)-aging characteristic parameter surveillance method［J］.Journal of Solid Rocket Technology，2005，28(4):271-275(in Chinese).

［2］ 张仕念，易当详，宋亚男，等.固体推进剂多失效模式相关的贮存可靠性评估［J］.固体火箭技术，2007，30(6):525-528.Zhang S N，Yi D X，Song Y N，et al.Evaluation on storage reliability of solid propellant based on correlative failure modes［J］.Journal of Solid Rocket Technology，2007，30(6):525-528(in Chinese).

［3］ Fillerup J，Pritchard R.Service life prediction technology program，ADA397950［R］.Edwards:Air Force Research Laboratory，1998.

［4］ 杨根，赵永俊，张炜，等.HTPB推进剂贮存期预估模型研究［J］.固体火箭技术，2006，29(4):283-285.Yang G，Zhao Y J，Zhang W，et al.Investigation on prediction model for storage life of HTPB propellants［J］.Journal of Solid Rocket Technology，2006，29(4):283-285(in Chinese).

［5］ 尤琦，赵宇，胡广平，等.基于时序模型的加速退化数据可靠性评估［J］.系统工程理论与实践，2011，31(2):328-332.You Q，Zhao Y，Hu G P，et al.Reliability assessment using accelerated degradation data based on time series model［J］.Systems Engineering Society of China，2011，31(2):328-332(in Chinese).

［6］ 马小兵，王晋忠，赵宇.基于伪寿命分布的退化数据可靠性评估方法［J］.系统工程与电子技术，2011，33(1):228-232.Ma X B，Wang J Z，Zhao Y.Reliability assessment using constant-stress accelerated degradation data based on pseudo life distribution［J］.Systems Engineering and Electronics，2011，33(1):228-232(in Chinese).

［7］ 尤琦，赵宇，马小兵.产品性能可靠性评估的时序分析方法［J］.北京航空航天大学学报，2009，35(5):644-648.You Q，Zhao Y，Ma X B.Performance reliability assessment for products based on time series analysis［J］.Journal of Beijing University of Aeronautics and Astronautics，2009，35(5):644-648(in Chinese).

［8］ Huang W，Duane L.An alternative degradation reliability modeling approach using maximum likelihood estimation［J］.IEEE Transactions on Reliability，2005，54(2):310-317.

［9］ Sun Q，Zhou J L，Zhong Z，et al.Gauss-Poisson joint distribution model for degradation failure［J］.IEEE Transactions on Plasma Sciences，2004，32(5):1864-1868.

［10］ 张昊，庞爱民，彭松.方坯药预测寿命与发动机推进剂药柱实际寿命差异研究［J］.固体火箭技术，2005，28(1):53-56.Zhang H，Pang A M，Peng S.Investigation on the differences between predicted lifetime of propellant carton and actual lifetime of motor propellant grain［J］.Journal of Solid Rocket Technology，2005，28(1):53-56(in Chinese).

［11］ 洪东跑，马小兵，赵宇.利用变环境数据的可靠性灵敏度分析［J］.兵工学报，2011，32(3):341-347.Hong D P，Ma X B，Zhao Y.Reliability sensitivity analysis using variable environment test data［J］.Acta Armamentarii，2011，32(3):341-347(in Chinese).

［12］ 洪东跑，马小兵，赵宇.利用变环境数据的 Weibull分布可靠性综合评估［J］.北京航空航天大学学报，2012，38(11):1487-1491.Hong D P，Ma X B，Zhao Y.Integrated reliability assessment for Weibull distribution using varied environment data［J］.Journal of Beijing University of Aeronautics and Astronautics，2012，38(11):1485-1491(in Chinese).

［13］ Uusipaikka E.Confidence intervals in generalized regression models［M］.London:Chapman ＆ Hall/CRC，2009.

［14］ 洪东跑，马小兵，赵宇.基于比例风险模型的可靠性综合评估［J］.系统工程与电子技术，2010，32(10):2132-2135.Hong D P，Ma X B，Zhao Y.Integrated reliability assessment based on proportional risk model［J］.Systems Engineering and Electronics，2010，32(10):2132-2135(in Chinese).

［15］ Kalbfleisch J D，Prentice R L.The statistical analysis of failure time data［M］.Hoboken:John Wiley ＆ Sons，2002.