基于关联矩阵的高速公路标识站优化选址模型与算法研究

王 握，张 晗，任仲山，刘 俊，彭 攀，林 雄

（东南大学 智能运输系统研究中心，江苏 南京 210096）

基于关联矩阵的高速公路标识站优化选址模型与算法研究

王 握，张 晗，任仲山，刘 俊，彭 攀，林 雄

（东南大学 智能运输系统研究中心，江苏 南京 210096）

为了进一步研究高速公路路径识别中标识站选址问题，以路网拓扑结构为基础，采用生成树理论对标识站的优化选址进行了分析。首先，给出了标识站选址原则，并根据图论的相关理论基础，提出了标识站的选址定理，确定了标识站的最优数量。然后，建立了标识站选址的优化模型，根据数量最少和OD反推原则确定了标识站选址的约束条件，通过流量较小的原则建立标识站最优选址的目标函数。同时，提出了基于关联矩阵实现大型路网标识站最优选址的算法。最后，通过算例阐述了利用模型解决高速公路标识站选址问题的求解过程。计算结果表明，该模型能够实现标识站的最优选址，符合高速公路联网收费中通行费精确拆分的实际需求。

高速公路；路径识别；标识站选址；生成树；关联矩阵

0 引言

随着联网收费的推行和高速公路网的形成，如何实现车辆路径的识别成为高速公路联网收费的核心问题。

在国外，很少对高速公路实行收费，或者仅对极少路段或者少数车型进行收费，不存在国内对整个高速公路网络进行封闭式收费的情况，因此车辆路径的识别研究相对较少，主要集中在卫星定位[1]、ETC电子不停车收费上[2-4]。

在国内，早前的研究多是以交通分配的理论方法对车辆进行路径识别，如最短路径法[5]、抽样调查法[6]、多路径容量限制法[7]、布瑞尔分配法[8]等。由于这些方法不能精确地获取每辆车的行驶路径，往往容易导致各高速公路公司通行费拆分不均，存在较大的争议。

随着技术的发展，为了实现通行费公平、合理拆分，精确识别车辆行驶路径已经成为实现联网收费的重要方法。目前常用的精确识别技术主要有基于车辆牌照的识别技术[9]、基于RFID标签的识别技术[10]、基于卫星定位的路径识别技术[11]，最新的一些精确识别技术主要有基于LBS定位[12]、基于RFSIM[13]等。这些方法的基本原理是通过在二义性路径的必要路段设置标识站，来对车辆的行驶轨迹进行识别。

在精确识别的方法中，标识站的合理选址是正确识别车辆行驶路径、精确收费和通行费拆分的关键。如何通过最少的标识站，在最低的投资成本下，实现车辆的路径识别成为路网管理中的重要工作。高洁等[14]运用支撑树理论，提出了适合大型路网的标识站选址算法和标识站数量确定方法，但该方法仅对单一的环状路网进行了分析，容易造成重要路段标识站数量不足或冗余的情况。丛浩哲等[15]采用深度优先搜索算法实现了高速公路标识站的选址和标识站数量的确定。赵艳红等[16]提出了网状路网下的多路径识别模型和清分算法。但该方法中标识站的选址没有从整个路网来考虑，且未考虑交通流量等的影响。苏晓明等[17]提出了一种基于概率模型的二义性路径标识站设置方法，用于解决高速公路网二义性路径标识站设置数量和设置位置的问题。该方法需要获取任一OD点对中多条竞争性路径的先验概率，对于大型路网而言，首先需要调查计算得到任一OD点对之间的竞争性路径，获取各条竞争性路径的先验概率，前期的调查工作量巨大，适应性差，比较适合应用于小型路网标识站的选址问题。

上述标识站选址的相关研究中，能够得到标识站最优设置数量和标识站的选址布局方案，但并没有考虑到复杂的收费网络，在最优标识站数量下，标识站的选址布局方案并不是唯一的，存在布局方案的优化选择问题。本文提出了基于关联矩阵的高速公路标识站优化选址模型和算法，能够得到标识站的最优选址方案，实现车辆路径的精确识别和保证各高速公路公司之间公平合理地进行通行费拆分。

1 基于路径识别的标识站选址原则

高速公路网可以抽象为连通图G=(V,E)，其中V(G)表示图G中的节点集合，E(G)表示图G中的路段集合。同时，p(G)表示图G中的节点数量，q(G)表示图G中边的数量，因此高速公路网中标识站的选址问题可以转化为在连通图中寻找合适的边设置标识站的问题。对于大型路网的标识站，其选址方案众多，应考虑如下几点原则。

1.1 流量最小原则

在路网中，标识站对经过的每一辆车进行身份信息（如车牌、车主等）采集，同时根据标识站所在的路段信息和车辆的出入口（收费站）信息，从而可以正确标定车辆的行驶路径，即需要对经过标识站的每一辆车进行路径匹配的计算。如果标识站所在路段车流量较小，对这些车辆的路径进行匹配计算的工作量就相对较少，同时当标识站出现故障时，能够保障不能识别出行驶路径的车辆数较小。综合考虑，标识站应设置在车流量较小的路段上。

1.2 数量最少原则

考虑到高速公路的投资和运营维护管理，在路网中设置的标识站数量应尽可能少，以减少标识站的投资建设成本和后期的运营维护管理成本。

1.3 OD反推原则

为了保证通行费在各路公司之间的精确拆分，需要获取每一辆车在路网中的行驶路径，即能够根据路网中标识站采集得到的车辆身份信息，结合车辆的出入口（收费站）信息，能够唯一确定车辆在路网中的行驶路径。

2 标识站选址相关定理和指标

结合图论中的相关原理，对余边集的概念进行了定义：对于连通图G而言,T为连通图G的一棵生成树，则在图G中关于生成树T的余边集RT= E(G)-E(T )，余边集RT中所含边的数量为number (RT)。

定理1：要对一个图G中的车辆进行精确的路径识别，标识站应该设置在余边集RT上，且标识站的最优数量为余边集中边的数量number(RT)[14]。

在路网中，设置标识站的边，可以看成是两条不直接相连的边，标识站可以看成是图中新加入的两个节点，如图1所示，在原路网图G中加入标识站后组成的新图G′。

图1 原图、生成树和加标识站的新图

因此车辆的行驶路径可以由OD点和标识站的信息进行确定。根据生成树的特性，生成树中的路段和路径是唯一确定的，一条已知OD的路径是由有标识站的路段和没有标识站的路段（生成树的边）组成，或者全部由没有标识站的路段组成，因此根据车辆的OD信息和车辆经过标识站的信息，车辆的路径是唯一确定的。如果标识站的数量少于number(RT)，则会导致任意OD点之间的路径不能唯一被识别，同时，当标识站的数量多于number(RT)，虽然任意OD点之间的路径能够唯一识别，但标识站出现冗余，不是最优的投资建设方案。

定理2：在连通图G的关联矩阵B中，线性相关的列向量对应的边不能组合成生成树中的边。

图G的生成树T的边数为p(G)-1，其关联矩阵是秩为p(G)-1的[p(G)-1]×[p(G)-1]矩阵，因此生成树T的关联矩阵的行向量线性无关，同时列向量也线性无关；在[p(G)-1]×[p(G)-1]的矩阵中，如果存在列向量线性相关，则关联矩阵的秩一定小于p(G)-1，即存在列向量可以被其他列向量表示的情况，因此该关联矩阵中列向量对应的边不能构成一棵生成树，充要条件满足，定理2成立。

指标1：根据标识站数量最少和OD反推原则，提出标识站数指标：

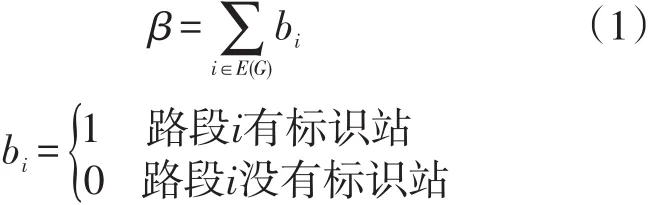
指标2：根据流量最少原则，提出流量比指标：

式中：RT为路网G中生成树T的余边集；E(G)为路网G中边的集合；qi为路段i上的交通量。

3 标识站优化选址模型的建立

根据数量最少和OD反推原则，结合定理1，标识站的选址问题可以转化成求路网G中生成树T的余边集RT的问题；根据流量较少的原则，标识站的选址存在最优选址的问题。因此标识站优化选址模型的数学描述如下：通过寻找路网G中的生成树T和其对应的余边集RT，使得设置标识站路段（余边集RT）检测到的交通量最小，因此模型可以描述如下。

目标函数为：

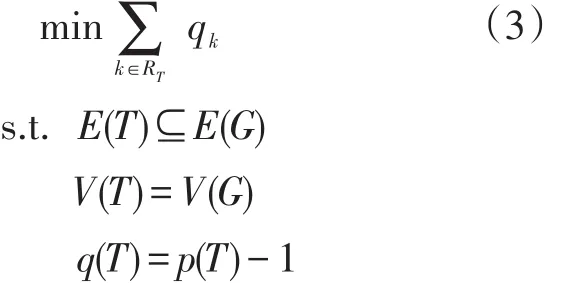
式中：G为高速公路的路网拓扑图；T为图G的一棵生成树；RT为余边集；E(T)为生成树T的边的集合，即路网中路段的集合；V(T)为生成树T的顶点的集合，即路网收费站的集合；q(T)为生成树T中边的数量； p(T)为生成树T中顶点的数量；qk为第k边上的车辆数。

4 标识站优化选址算法

标识站选址问题，可以等价于求图的生成树问题和组合优化问题。因此可以采用经典的求图中生成树的算法，如Prim算法[18]、Kruskal算法[18]、破圈法和避圈法[19]，来求解标识站选址的问题。但这些算法只能求出图中的部分生成树，即只能得到部分余边集，因此不一定能够得到最优的标识站选址。同时，选址算法要求求得所有的选址方案，因此存在求解所有生成树的问题，对于大型路网而言，这些方法显然是不适用的。同时，对于存在求解所有生成树的算法，如对偶展开树算法[14]、广度优先搜索和深度优先搜索算法[18]等，容易出现系统的堆栈容量限制，递归容易溢出的情况。本文提出了一种较为高效的可行方法，能够适合于大型路网标识站的优化选址问题。

4.1 算法的基本思想

模型的求解分为两部分：第一部分是路网中所有余边集的求解（标识站的选址方案）；第二部分是最优余边集的选择（最优标识站选址）。

路网图G中余边集的求解是通过寻找图G中不能组合成生成树的边集组合（关联矩阵的线性相关列向量组），从而通过间接得到图G所对应的所有生成树来求解对应的余边集。

在余边集的求解中，得到的余边集全部满足模型的约束条件，因此仅需找到满足目标函数的余边集即可求得最优余边集。

4.2 算法步骤

Step1：构造无向路网图G的完全关联矩阵Ar：

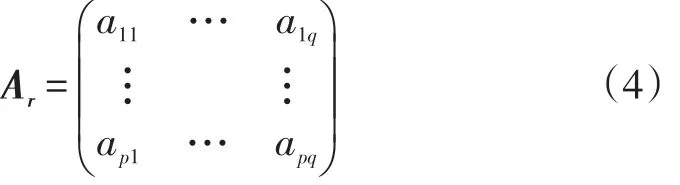
Step2：将矩阵Ar中的每一列向量中第一个值为1的元素的取值改为-1，得到新的完全关联矩阵A1。这样做的目的是保证完全关联矩阵A的秩为p(G)-1，便于后面的矩阵运算；

Step3：删除完全关联矩阵A1中的任意一行，得到关联矩阵A2，矩阵A2的秩为p(G)-1；

Step4：求关联矩阵A2的极大线性无关的列向量组H：β1,β2,…,βm（其中m=p-1），剩下的列向量组K：θ1,θ2,…,θn（其中n=q-p+1），对矩阵A2的列向量重新排序得新的矩阵 A={β1,β2,…, βm,θ1,θ2,…,θn}；

Step5：找出满足如下条件的系数项τ1,τ2,…, τm,δ1,δ2,…,δn，可知系数不为零的列向量对应的边不能组合成生成树，即可以反推得到所有的生成树组合；

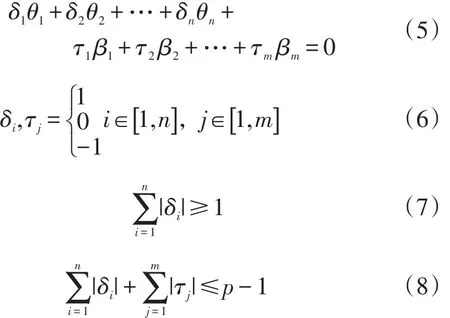
Step6：根据余边集的定义，可以计算得到所有生成树的余边集；

Step7：最优余边集的选择：在余边集的求解中，得到的余边集全部满足模型的约束条件，因此仅需找到满足目标函数的余边集。

5 实例分析

在一个有11个节点、16条边的路网G中，其节点集V={1,2,3,4,5,6,7,8,9,10,11}，边集E= {a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p}，路网G中边节点对应的关系、各路段的权值（路段的里程，单位：km）和各路段流量如表1、图2所示。

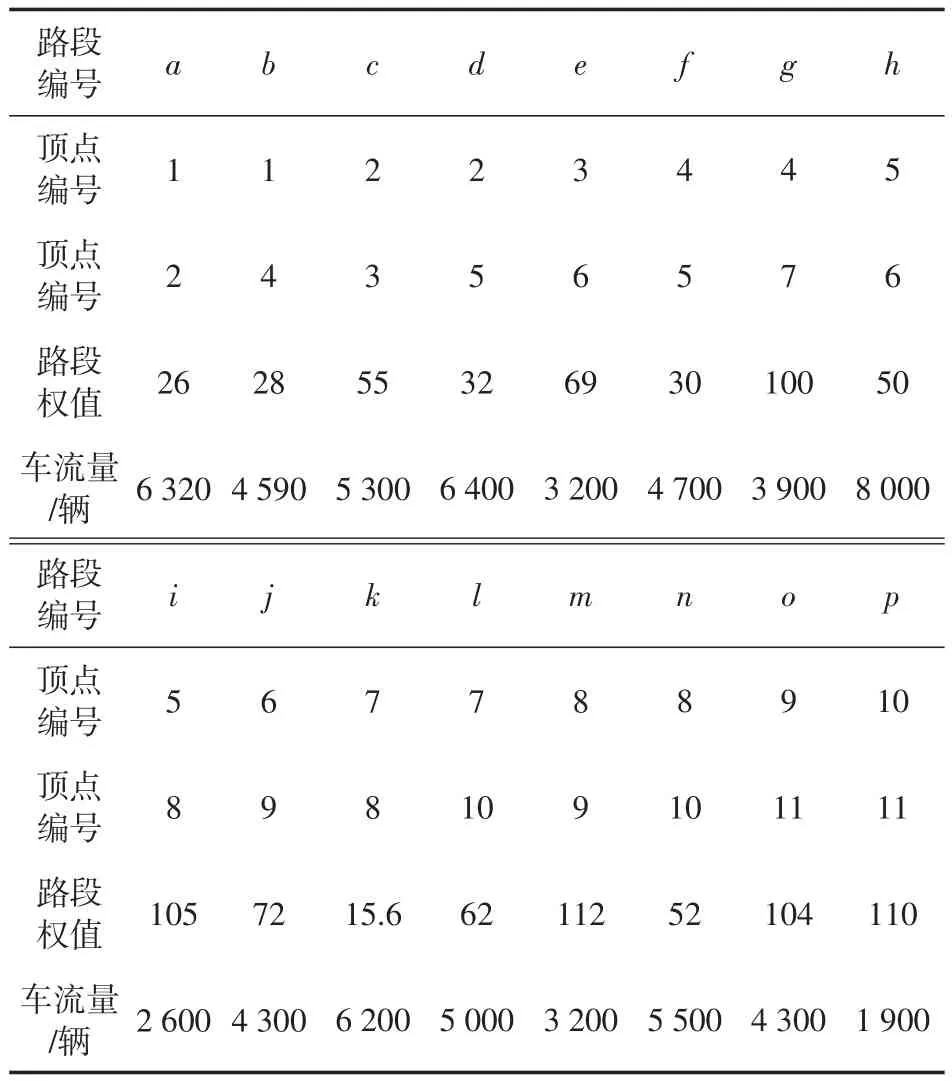
表1 路网结构及属性表

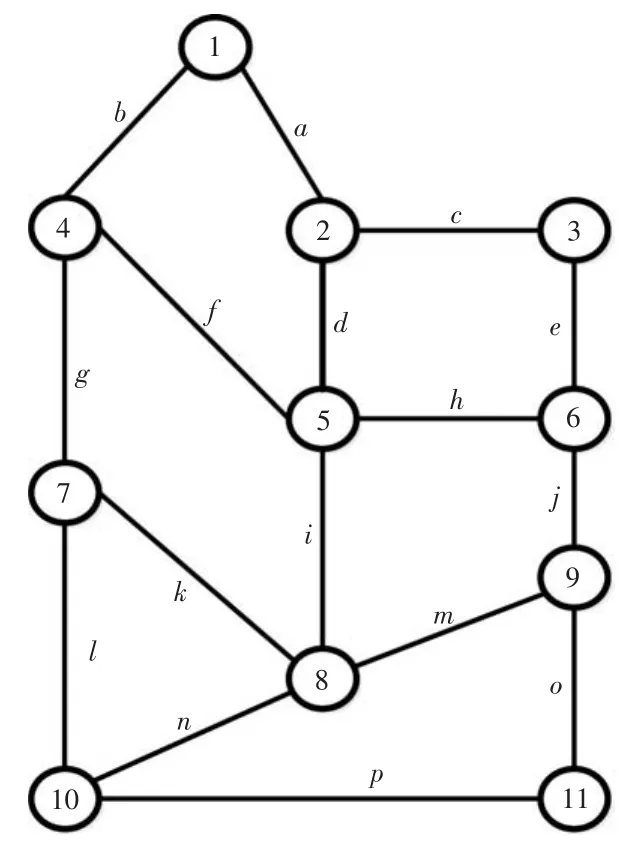
图2 实例路网G

根据完全关联矩阵的定义，得到路网G的完全关联矩阵Ar：

将矩阵Ar中的每一列向量中第一个值为1的元素的取值改为-1，得到新的完全关联矩阵A1，删除A1任意第n行数据，本文取n=11，得到10× 16、秩为10的矩阵A2。

通过初等行变换，矩阵A2的极大线性无关的列向量组H为边a,b,c,d,e,g,i,j,l,o对应的列向量，剩下的列向量组K为边f,h,k,m,n,p对应的列向量，通过对矩阵A2的列向量重新排序，得矩阵A：

通过对矩阵A的列向量进行简单的线性运算，找出边f,h,k,m,n,p所对应的列向量之间以及与极大线性无关组H中列向量的相互线性关系。通过计算得到了不能组合成生成树的边集组合为6 035种，能够组成生成树的边集组合为1 703种。根据余边集的定义，同理可知余边集的组合为1 703种，即标识站的选址方案为1 703种。

将根据上述计算得到的余边集组合，代入模型的目标函数中，可以得到不同选址方案中标识站检测得到的车流量总和，如图3所示。

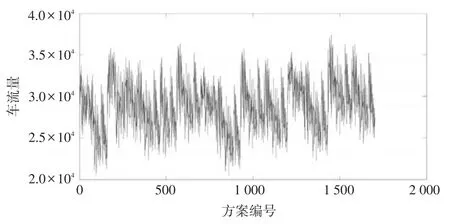
图3 不同方案下标识站车流量总和

从图3中可以看出，在1 703种选址方案中，不同选址方案下标识站检测得到的车流量相差较大，因此需要对标识站进行最优选址。最终通过比选，其中第861号方案中标识站数β=6为最优标识站数，流量比η=27.2%在所有选址方案中最小，即该方案为最优选址方案，标识站应设置在路段b,e,i,l,m,p上。

从图中可以得到，最不理想的标识站选址方案为第1 452号方案，即标识站设置在路段a,d,l,h, k,n上，检测得到的流量最大，共计37 420辆，流量比η=49.6%。因此在不考虑同一车辆经过多个标识站的情况，即37 420辆车在路网中需要进行路径匹配，数据计算量较大。当标识站设置在最优余边集路段b,e,i,l,m,p上时（如图4所示），标识站检测得到的流量最小，共计20 490辆，流量比η= 27.2%，相对最不理想的标识站选址，可以减少对22.4%的车辆进行路径匹配，数据计算量相对较少。因此，可以看出标识站最优选址能够最大限度地减少路网中需要进行路径匹配的车辆数，从而提高整个路网车辆路径识别的效率。

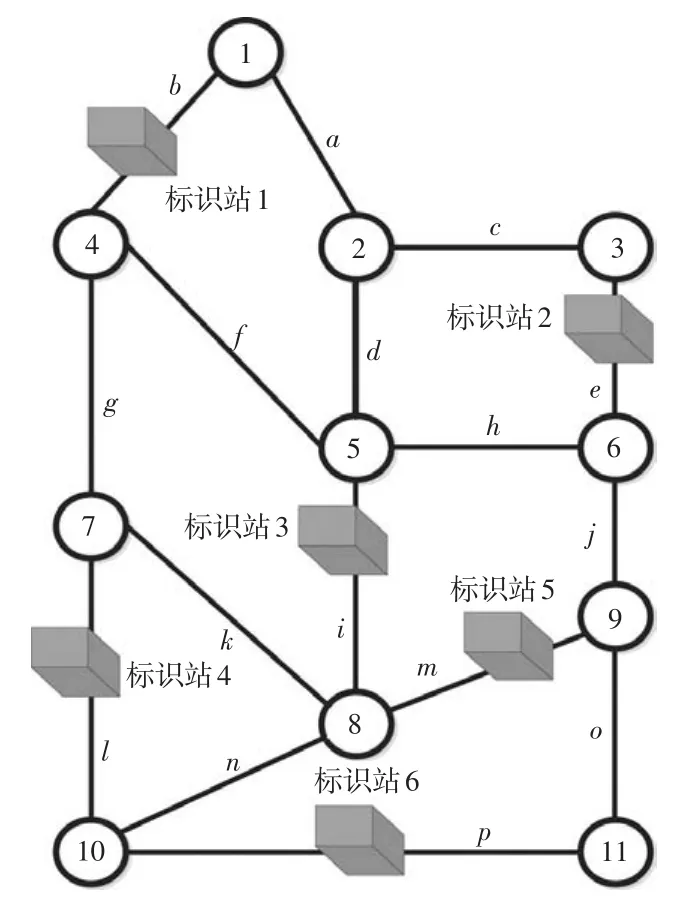
图4 路网标识站最优选址方案

6 结语

随着公路建设投资的加大，为保障各高速公路公司的合法权益，实现高速公路网通行费的精确拆分和车辆行驶路径的精确识别已成为必然的发展趋势。本文所建立的高速公路标识站优化选址模型和基于关联矩阵的求解算法符合高速公路联网收费中通行费精确拆分的实际需求，具有较强的通用性，能够适用于复杂的高速公路收费网络，为高速公路标识站的建设提供理论和技术上的支持。然而，在标识站的优化选址和数量选择上，并没有考虑标识站损坏、冗余布局及标识站的识别准确率对车辆运行路径匹配的影响，下一步的研究中将加以考虑。

[1] 周崇华.德国高速公路卡车收费政策实施及成果分析[J].上海公路，2008（3）：56-60.

[2] 强文萍.高速公路联网收费系统技术研究[D].西安：长安大学，2002.

[3] 陈爱英.长三角高速公路ETC联网收费管理模式研究[D].南京：东南大学，2005.

[4] 高祥，张晓升.日本高速公路电子收费的管理运营模式[J].中国交通信息化，2011（1）：24-27.

[5] CHUK C.Decentralized Control of High Speed Vehicle Strings[J].Transportation Research,1974,8(3):362-383.

[6] BARBIERI E.Stability Analysis of a Class of Interconnected System[J].ASME Journal of Dynamic System,Measurements,Control,1993,115(3):546-551.

[7] 刘海涛，白敬.多路径容量限制法在公路收费系统的应用[J].天津城市建设学院学报，2005，11（3）：179-183.

[8] 陈洪星，孙洋.改进的布瑞尔交通分配模型在高速公路路径识别问题中的应用[J].交通理论，2008（12）：37-40.

[9] 杨佳莉.基于车牌识别的高速公路网多路径精确识别研究[D].西安：长安大学，2014.

[10] 张昊.基于RFID的浙江省高速公路联网收费多义性路径识别研究[D].长春：吉林大学，2009.

[11]王东柱，宋向辉，李亚檬.卫星定位不停车收费中基于决策圈的路径识别方法[J].公路交通科技，2011，28（5）：102-107.

[12]陈良.基于移动LBS的高速路网多路径识别关键技术研究[D].成都：电子科技大学，2013.

[13]李莹，李鸿，陈艺廷.基于RFSIM路径识别的高速公路收费系统设计[J].现代电子技术，2014，37（1）：60-63.

[14] 高洁，施其洲.高速公路标识站选址模型与算法研究[J].公路交通科技，2008，25（1）：139-141，145．

[15]丛浩哲，姜杰.基于支撑树法的高速公路多路径识别问题研究[J].交通与运输：学术版，2007（7）：80-83.

[16]赵艳红，刘发胜，任传祥，等.网状高速公路网下的多路径识别模型与费用清分算法[J].公路，2008（5）：110-114．

[17]苏晓明，徐东彬.基于概率模型的二义性路径识别标识站设置方法[J].公路交通科技，2013，30（4）：119-123.

[18] 李春萍，陶红艳，金晶，等.数据结构与算法教程[M].北京：清华大学出版社，2007.

[19] HLADOVERS E.Longitudinal Control of Automated Guideway Transit Vehicles Within Platoons[J].Journal of Dynamic System,Measurements,Control,1978,100(4):301-310.

Optimal Locating Model andAlgorithm of Identification Station of Expressway Based onAssociated Matrix

WANG Wo,ZHANG Han,REN Zhong-shan,LIU Jun,PENG Pan,LIN Xiong
（Intelligent Transport System Research Center of Southeast University,Nanjing 210096,China)

In order to further study the location of identification station in expressway routes identification,based on road network topology,the optimal location of identification station were analyzed by using spanning tree.Firstly,the principles were summarized,and location theorem was put forward according to the relevant theoretical basis of graph theory,and the optimal numbers of identification station were given.Then,optimal locating model of identification station was established,the restrictions of identification station location were determined based on the principle of minimum number and O-D estimation,and objective function was established based on the principle of road section with small flow. And based on associated matrix,the algorithm which was suitable for optimal location of identification station in large-scale road network was proposed.Finally,the solving processes applying the optimal locating model to solve the location of expressway identification station were expounded with a numerical example.The results show that the model achieves good effect on the optimal location of identification station,which meets the actual needs of precise toll allocation in networking toll.

expressway;route identification;location of identification station;spanning tree;associated matrix

U491

A

2095-9931（2015）06-0064-07

10.16503/j.cnki.2095-9931.2015.06.011

2015-07-06

王握（1992—），男，湖南益阳人，硕士研究生，主要研究方向为智能交通。E-mail：m15850570887@163.com。