基于熵权模糊物元的轨道交通运营安全评价

汪 勇，吴丽霞，蔡 明

（重庆交通大学 交通运输学院，重庆 400074）

基于熵权模糊物元的轨道交通运营安全评价

汪 勇，吴丽霞，蔡 明

（重庆交通大学 交通运输学院，重庆 400074）

为解决轨道交通运营安全评价过程中定性指标难以量化以及分级量值范围界定模糊等问题，在模糊物元分析的基础上，引入熵值法确定指标权重，并利用欧氏贴近度反映待评安全结果与标准安全结果互相接近的程度，建立了一种评价轨道交通运营安全指数的熵权模糊物元模型。在总结前人研究成果的基础上，将城市轨道交通运营安全评价指标体系中的各指标划分成“优”、“良”、“一般”、“差”4个评判等级，并给出了各等级的适用范围。以重庆市轨道交通3号线为例，对比可拓物元法进行分析，结果显示熵权模糊物元法评价指标值为0.588 9，可拓物元法评价风险等级为3级，评价安全程度均在良好以上，这表明熵权模糊物元模型能够有效地解决非定量化的评价问题，对比可拓物元模型，评价精度有进一步提高。

轨道交通；安全评价；模糊物元模型；熵权；欧式贴近度

0 引言

轨道交通作为城市客运公共交通的重要载体，承担着大量的客流运输任务，且客流封闭集中，一旦发生紧急情况，很难在第一时间得到响应。轨道交通运营安全的影响因素复杂多样，因涉及的行业领域跨度大，评价指标也同样因人或因地而异，难以用数学量化的形式进行表达。

轨道交通安全研究一直是交通安全研究的重点领域，也是国内外专家学者研究的热点。相比而言，国外相关研究内容丰富，诸多成果更贴近于实际；国内研究起步虽晚但发展较快，研究内容更加细化。

英国伦敦轨道安全评价是通过直观的伤亡事故与事故原因的定量数据来确定不同风险因素的伤害程度，此类方法对原始数据的依赖程度很高，适合经验丰富的发达国家[1]。韩国铁道研究中心于2005年提出风险评估程序、风险分析模型以及风险管理架构，后来均实际运用于韩国城市轨道交通网络安全评估，并取得了可观的成效[2-3]。随后两年，西班牙政府制定了围绕“安全、可靠、优质”三个目标的地铁质量安全计划，通过更新现有的硬件设备来提高紧急情况下的地铁安全应对能力，这样做效果明显，但投资过大[4]。

国内学者刘书浩等[5]通过对英国城市轨道交通运营安全状况的研究，提出了一些符合我国当下国情的政策建议，为国内轨道交通安全的定量评价提供了定性的框架。王艳辉等[6]采用增益型加权综合法对筛选指标进行了计算，并通过Matlab进行仿真模拟，评价方法科学合理，但没有对多级指标的阈值进行细化设置，评价精度有一定的局限性。郭湛等[7]利用层次分析法（Analytic Hierarchy Process，简称AHP）组建了轨道交通安全性评价指标体系，通过求解判断矩阵的特征值与特征向量来确定各个指标的权重，最后计算一致性指标，该方法对轨道交通安全评价体系进行了系统科学的界定。蔡国强等[8]利用神经网络法构建了模糊穴模型，提出一种基于模糊穴映射理论的轨道交通安全评估方法，它从轨道交通系统的动态演变性出发，分析了系统的内部结构、外部属性和整体状态的动态演变机理，实践表明该方法在改善主动安全预警水平中具有良好的效果。

上述国内外研究人员均对轨道交通安全评价体系有着科学、独到的见解。由于轨道交通系统复杂，运营安全评估需要多指标共同决策进行，单一的评价方法无法客观地满足评价的科学性，而不同评价指标间跨度大，难以归类相容，这也是有关安全评价指标选取成为专家学者研究热点的原因。研究发现，组合物元理论提供了解决这一问题的思路。

为了较大限度地避免轨道交通系统中评价标准的不确定性与不唯一性带来的影响，本文基于模糊物元分析理论，将熵权法与欧式贴近度的概念相融合，建立了轨道交通运营安全程度评价的熵权模糊物元模型。该模型是一种集合多种理论将多元数据进行量化评价的新方法[9]，它通过引入熵权法确定评价指标的权重配比，同时利用欧氏贴近度对评价指标进行跨度分类，将不同领域的指标参数进行量化配比。

1 熵权模糊物元模型的建立

熵权模糊物元模型既可从横向上比较不同地区的交通变化状况，又可从纵向上衡量各地区交通状况发展的趋势[10]，具体采用模糊物元分析方法来建立交通安全评价模型，从分析确定影响交通安全的因素入手，应用信息熵的概念和熵权模糊物元模型计算各时期待评样本与标准样本的欧氏贴近度，进而得知交通安全的变化情况，从而实现不同地区交通变化状况的横向比较，同时在纵向上对各地区交通状况发展趋势加以衡量[10]。该模型还可选择不同评价地区，计算某一时期各地区待评样本与标准样本的欧氏贴近度，从而得出不同地区在同一时期的交通安全状况[11]。熵权模糊物元模型有关轨道交通运营安全状况的评价流程如图1所示。

图1 评价流程

1.1 物元理论

物元即是通过有序的三元组R=（N,C,u）来描述事物的基本元，其中N为给定名称的事物，C为特征，u为关于特征C存在的量值。若三元组事物N中的量值u存在模糊性，则将此类包含模糊量值u的物元称为模糊物元，记作[11]：

式（1）中：R,N,C分别表示对应的模糊物元、名称事物以及事物N的特征；根据上述物元理论的定义，则u（x）表示对应特征C的模糊量值，即三元组R中事物N关于特征C对应量值x的隶属度。

对于轨道交通安全评价体系而言，N为评价体系样本（即轨道交通安全程度），C为评价体系指标，u（x）为评价体系样本N（轨道交通安全程度）对于评价体系指标C相应指标值的隶属度。

1.2 定义复合模糊物元

假定轨道交通安全评价体系样本N中存在n个待评指标C1,C2,…,Cn，与之相应的模糊量值为u（x1）,u（x2）,…,u（xn），称R为n维模糊物元。若以Rmn表示m个评价样本n维复合模糊物元，则u（xij）为第i个样本第j项评价指标对应的模糊量值（i=1,2,…,m;j=1,2,…,n），记作[11]：

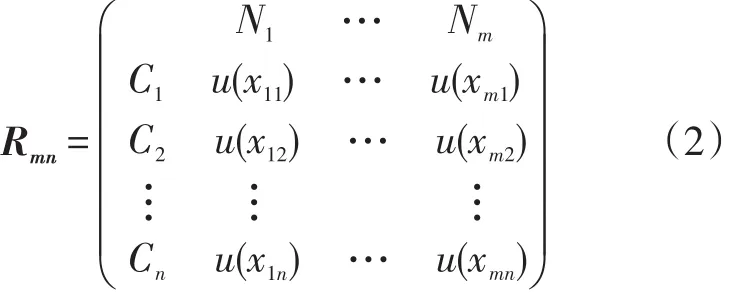
1.3 从优隶属原则

通过从优隶属度建立的原则即为从优隶属度原则。从优隶属度为各单项待评指标Cn相应的模糊量值从属于标准样本对应评价指标相应模糊量值的隶属程度。对于不同评价样本来说，各评价指标可划分为两种[11-12]：

（1）越小越优型评价指标

（2）越大越优型评价指标

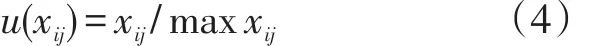
式（3）、式（4）中：xij表示第i个样本第j项评价指标对应的量值；min xij,max xij分别表示各待评指标所有量值的最小值与最大值。

1.4 构造差平方复合模糊物元

构造样本n维标准模糊物元R0n，其中各项为复合模糊物元Rmn各项待评指标中从优隶属度的最小值或最大值：

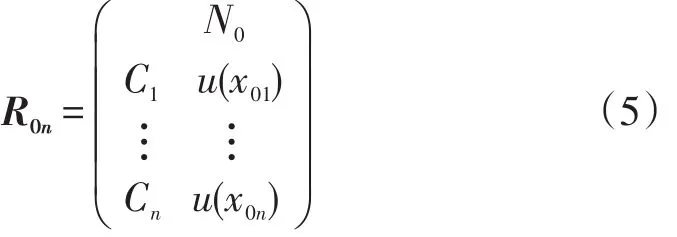
以Δij（i=1,2,…,m;j=1,2,…,n）表示标准模糊物元R0n与复合模糊物元Rmn各项的差的平方，得到差平方复合模糊物元：

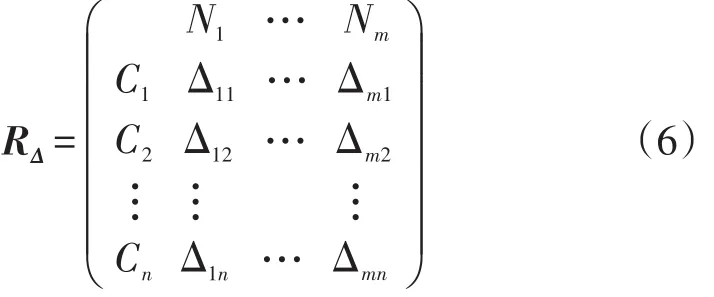
常见的评价体系中有关权重的确定方法有：层次分析法、Delphi法（德尔菲法）、特征向量法以及对比打分法等。在轨道交通运营安全评价中，不同待评指标跨度领域大，对各评价单元的影响程度不同，需要根据其对评价单元的贡献大小确定相应的权重。信息熵是反映信息无序化程度的变量，其值越大，说明系统越混乱，反之系统则越有序。评价指标变异程度越大，说明提供的信息量越大，所占权重也应越大[12-14]。由评价指标构建判断矩阵来确定指标权重，能在一定程度上消除人为权重计算的误差与干扰，使评价结果更为合理。

熵值法计算过程如下。

（1）构建m个事物n个评价指标的判断矩阵R=(xij)mn（i=1,2,…,m;j=1,2,…,n）。

（2）将所构建的判断矩阵作归一化处理，得到判断矩阵B。

对于越小越优型指标，存在[15]：

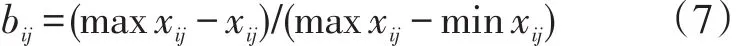
对于越大越优型指标，存在：

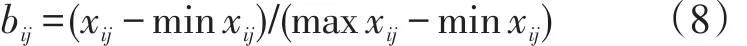
式（7）、式（8）中：min xij和max xij分别为同一评价指标下不同事物中最不满意者与最满意者。

试验用地基土采用龙岩市岩溶发育地区覆盖层的土体，土体主要为含碎石粉质黏土；采用淤泥模拟溶洞充填物，经烘干后碾碎，过5 mm的筛子，之后重新配制而成；砂垫层采用中粗砂，铺设厚度2 cm。土的物理力学指标如表1所示。

（3）定义熵：在m个评价事物n个评价指标的评价过程中，记第j个评价指标的熵值Hj为：

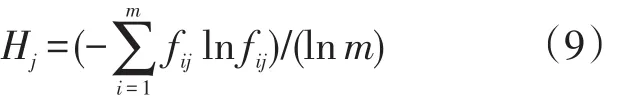
其中：

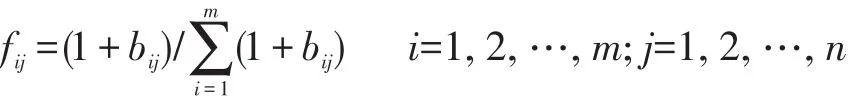
（4）计算熵权ωj为：

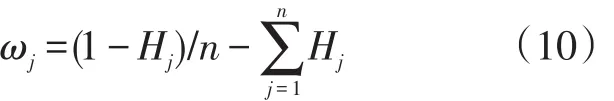
其中，0≤ωj≤1，且。

1.6 轨道交通运营安全评价与欧式贴近度

将贴近度的概念融入到轨道交通运营安全评价中，能够直观地反映待评指标安全结果与标准指标安全结果互相接近的程度，其值越小表示两者越疏远，反之则越接近。由此可以根据贴近度对指标方案进行分类。由于轨道交通安全评价属于综合系统性评价，所以采用先乘后加算法对欧式贴近度进行计算：

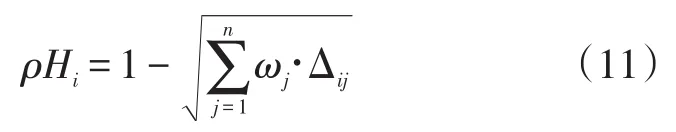
构建欧式贴近度复合物元模糊矩阵RρH如下[15]：

式（11）、式（12）中：ρHi（i=1,2,…,m）为第i个评价样本与标准样本之间相互接近的程度。参考ρHi的具体数值，通过横向对比即可对轨道交通安全程度进行评价。

2 案例分析

2.1 评价指标的选取

熵权模糊物元法是对选定指标的量化评价以及层次定位，但关于具体评价指标的选取并非本文研究的重点，需要根据历史数据以及前人所得成果进行定性化的选择。

本次对重庆市轨道交通3号线的指标选取，主要集中在客流、管理以及系统安全三个指标层面上，分别涵盖轨道交通的参与者、管理者以及载体，这也是影响轨道交通运营安全主要层面上的因素。在总结前人对城市轨道交通安全评价研究的基础上，根据《地铁运营安全安全评价标准》（GB/T 50438—2007）[16]、《城市轨道交通安全预评价细则》[17]、《公路项目安全性评价指南》（JTG/T B05—2004）[18]等相关资料，本文将城市轨道交通安全评价指标体系中的指标层次划分成4个评判等级：优、良、一般、差。

参考《重庆市轨道交通条例》[19]，根据对山地城市轨道交通运营安全评价各指标的分析，经过对重庆市轨道交通3号线早、中、晚高峰期的调查以及相关专家组咨询后，经过归一化处理，得到各子指标最终评价的标准量值。这些量值包括4个要素、5个事物、17个指标。基于前人对交通安全评价指标权重的解读[20-23]，本文对相应的评定等级及分值做一划分，并将指标量化结果列于表1。

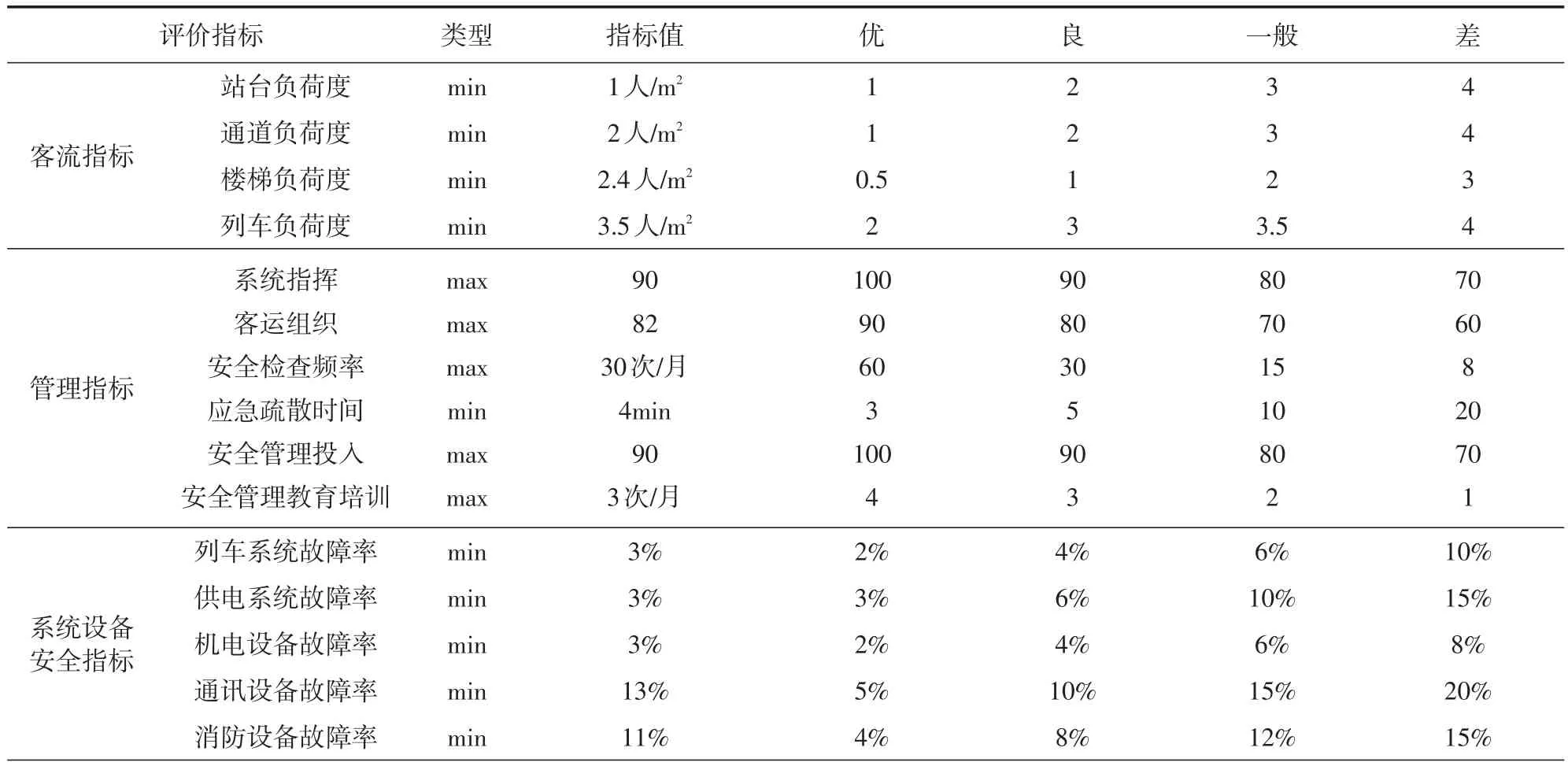
表1 轨道交通3号线运营安全评价指标

表1（续）

2.2 评价模型的建立

（1）根据表1中的数据构建5个事物、17个指标的复合模糊物元。其中4个主体要素指标中，客流、管理以及系统设备对轨道交通运营安全的影响最为突出。

客流指标与当地交通情况有着直接的关系，作为轨道交通服务的对象，客流指标直接反映轨道交通的服务水平与服务能力；管理指标是轨道交通运营安全的中心要素，包含对整个轨道交通系统流程的管理，是保证系统正常运行的重点；系统设备指标是轨道交通运营安全的关键要素，它与轨道交通安全直接挂钩，在轨道交通运营过程中，系统设备不允许出现任何问题；外界环境指标因地而异，不具备统一性与完整性，但作为轨道交通的外部条件，其影响也不容忽视。

（2）根据评价指标的类型（越大越优型或越小越优型），将构建的复合模糊物元经式（3）、式（4）处理后，得到从优隶属度物元Rmn：

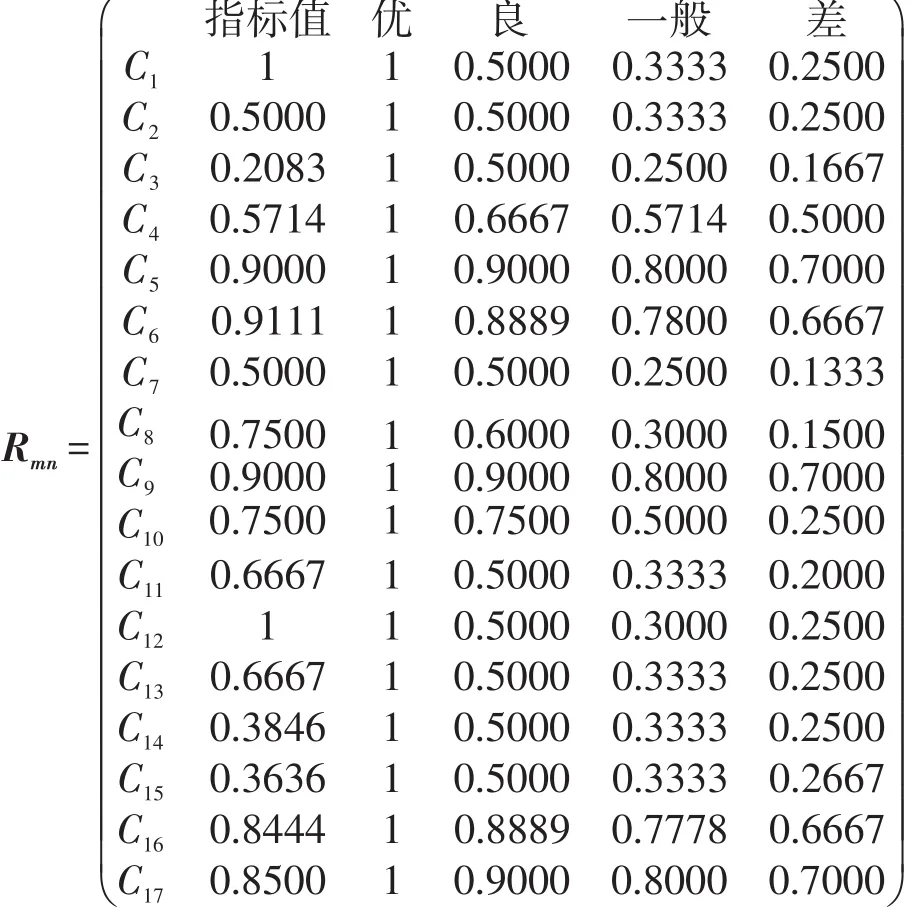
（3）由从优隶属度物元Rmn知各评价指标最优隶属度均为1，经过式（5）、式（6）处理后，得平方差复合物元如下：

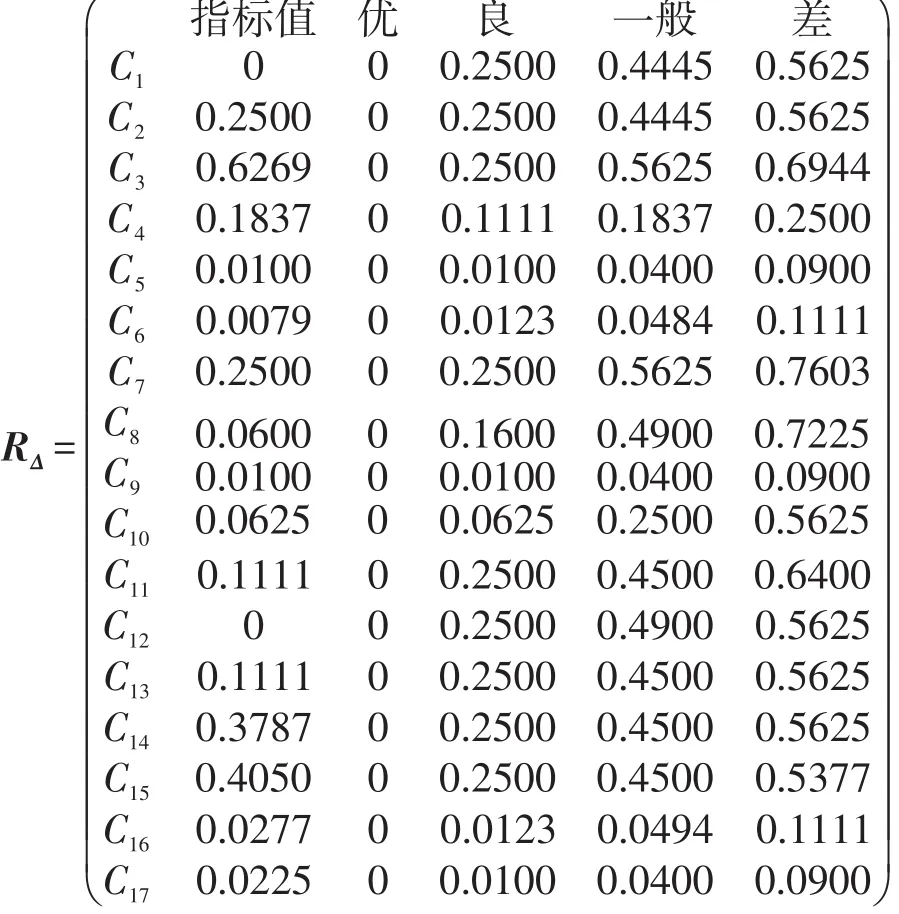
（4）通过熵权法计算各指标权重，将各评价指标的实际值作归一化处理，得判断矩阵B如下：

由判断矩阵B计算得熵权Hj和各指标的权重ωj分别如下：

最后得样本贴近度复合物元模糊矩阵RρH：

2.3 评价结果检验

熵权模糊物元法评价结果的指标值为0.588 9，位于评价等级的“优”（0.996 6）和“良”（0.585 6）之间，由此判断重庆市轨道交通3号线的安全程度为“良”以上。

利用二级可拓物元法[24]参照上述指标进行计算（因篇幅所限，详细计算过程不再赘述），结果分别如下。

（1）一级评价

客流指标关联度矩阵：

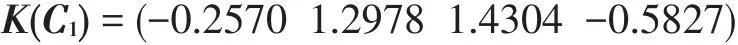
管理指标关联度矩阵：

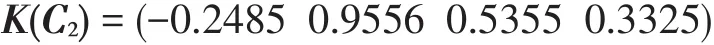
系统设备指标关联度矩阵：

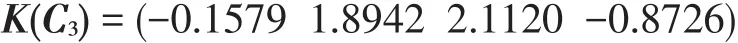
外界环境指标关联度矩阵：

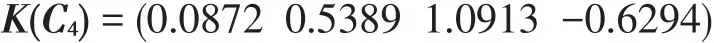
（2）二级评价

待评指标对各风险等级的关联度矩阵K(N)等于一级指标对各风险等级的关联度K(Ci)(i=1,2,3, 4)乘以一级指标的权重向量。经计算得：

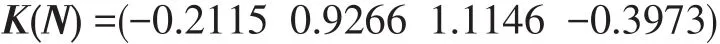
将二级可拓物元法对比熵权模糊物元法，结果如表2所示。

表2 两种方法对比结果

根据可拓物元法，maxKj(N)=K3(N)，由此可以判断重庆市轨道交通3号线的运营风险等级为3级（等级越高越安全），安全状况处于“良”，与熵权模糊物元法评价的结果基本一致。

2.4 评价结果分析

此次评价显示，重庆市轨道交通3号线运营情况为“良”，通过熵权模糊物元法（指标值为0.588 9），可定量反映评价结果更接近“良”，距离“优”尚有较大差距。系统的17个评价指标中，客流、管理以及系统设备指标占比近90%，在熵权归一化处理过程中，上述指标对整体评价结果起着关键性影响，而客流指标不随轨道交通的主体而改变。因此，提高管理水平、维持系统设备安全正常运行是保障轨道交通3号线安全运营的主要策略。熵权模糊物元法和可拓物元法的评价结果基本接近，但前者更能定量地描述指标值在评价等级中的位置，相比传统的物元评价方法有了更高层次的拓展与引申。

3 结论

整个轨道交通运营安全评估是一个复杂的系统工程，社会影响大，涉及因素多，特别是不同区域、不同方式的混合交叉运输，评价难度更大。因此，在进行详细的轨道交通运营安全评价时，需要根据各地区实际情况进行指标的定性筛选、补充以及标准的量化分级，只有这样，综合评价的结果才能客观、真实地反映当地轨道交通运营安全的程度，具体结论如下。

（1）轨道交通运营安全评价的定性指标量化和分级量值范围界定非常关键。采用熵权模糊物元法确定轨道交通运营安全程度，能够根据现实数据本身所反映的特性来计算各指标的权重，有效地避免权重分配时主观因素的影响，采用主观判断与主成分分析相结合的方法把握影响轨道交通运营安全的主要因素，使权重指标的分配更加合理。这种利用数据本身特点来反映数据结构与结果的评价模型，能够有效减少整个计算过程的主观性与人为影响，最大程度地减小误差。

（2）相比其他物元评价模型，熵权模糊物元模型一定程度上量化了待评指标与评价等级的关联程度，利用它可以建立多目标参数综合评判的物元模型，以数字的形式直观反映各指标间的关联，为轨道交通运营安全程度的提高提供了可量化的数据参考指标，可对预测结果进行量化定位。需要说明的是，本文仅从客观空间维度进行了多指标交通安全评价研究，而在资源数据充足的条件下，还可从时间领域多项比较整个轨道交通系统不同指标在不同时间段内的评价情况，这种跨空间、跨时间的双维度综合评价精度将会更高。

[1] REILLY J,BROWN J.Management and Control of Cost and Risk for Tunneling and Infrastructure Projects[J].Tunnelling and Underground Space Technology,2004,19(4): 329-330.

[2] PARK C W,WANG J B,KWAK S L,et al.Development and Application of Hazard Analysis&Risk Assessment Models for the Korea Railway[C]//Proceeding of the19th International Railway Safety Conference.Denver:International Railway Safety Conference,2008.

[3] PARK C W,WANG J B,KWAK S L,et al.Review and Assessment of the Korea Rail′s Safety Performance Using Risk Assessment Models[C]//Proceeding of the 20th International Railway Safety Conference.Bastad,Sweden:International Railway Safety Conference,2009.

[4] MADINAVEITIA J.Metro Network Quality Plan[C]//Proceeding of the 2007 Winter Simulation Conference.Washington D.C.:Winter Simulation Conference,2007.

[5] 刘书浩，贾文峥，杨远舟，等.英国城市轨道交通运营安全评估经验借鉴[J].交通标准化，2014，42（17）：58-60.

[6] 王艳辉，李曼，冯欢.增益型加权综合法在城轨交通运营安全评价中的应用[J].铁道学报，2013，35（3）：9-17.

[7] 郭湛，商小雷，李海.基于AHP的轨道交通安全评价体系模型[J].中国铁道科学，2011，32（3）：123-125.

[8] 蔡国强，贾利民，贾玉泉，等.基于模糊穴的轨道交通安全评估方法的研究及应用[J].模糊系统与数学，2008，22（2）：162-168.

[9] 车法，陈栓发，马庆雷，等.重载路面车辙评价物元模型构建及应用[J].广西大学学报：自然科学版，2010，35（4）：634-637.

[10]刘黎，徐逸伦，江善虎，等.基于模糊物元模型的城市活力评价[J].地理与地理信息科学，2010，26（1）：73-76.

[11] 田静宜，王新军.基于熵权模糊物元模型的干旱区水资源承载力研究——以甘肃名勤县为例[J].复旦学报：自然科学版，2013，52（1）：87-89.

[12]杨秋林，郭亚兵.基于熵权的模糊物元模型在城市生态安全评价中的应用[J].数学的实践与认识，2010，40（19）：62-66.

[13] 杨丽美，张维江.基于模糊物元模型的宁夏节水型社会效应评价[J].人民黄河，2013，35（5）：46-48.

[14] 施开放，刁承泰，左太安，等.基于熵权物元模型的耕地占补平衡生态安全评价[J].中国生态农业学报，2013，21（2）：244-249.

[15]刘娜，艾南山，方艳，等.基于熵权的模糊物元模型在城市生态系统健康评价中的应用[J].成都理工大学学报：自然科学版，2007，34（5）：589-594.

[16] 北京市地铁运营有限公司.GB/T 50438—2007，地铁运营安全评价标准[S].北京：建筑工业出版社，2007.

[17] 国家安全生产监督管理总局.城市轨道交通安全预评价细则[Z].北京：国家安全生产监督管理总局，2007.

[18]华杰工程咨询有限公司.JTG/T B05—2004，公路项目安全性评价指南[S].广州：广州出版社，2004.

[19] 重庆市人民代表大会常务委员会.重庆市轨道交通条例[Z].重庆：重庆市人民代表大会常务委员会，2011.

[20] 潘科，王洪德，石剑云.多级可拓评价方法在地铁运营安全评价中的应用[J].铁道学报，2011，33（5）：15-19.

[21] 马一太，曾宪阳，刘万福.地铁火灾危险性的模糊综合评判[J].铁道学报，2006，28（3）：106-110.

[22] 付印平，高自友，李克平.基于元胞自动机模型的地铁列车追踪运行研究[J].交通运输系统工程与信息，2008，8（4）：89-95.

[23] 张生瑞，邵春福，严海.公路交通可持续发展评价指标及评价方法研究[J].中国公路学报，2005，18（2）：74-78.

[24]马忠英，杨琦，周伟.基于物元模型的轨道公路协调发展多指标可拓评价[J].交通运输工程学报，2010，10（5）：97-101.

Operation SafetyAssessment of Rail Transit Based on Entropy Weight Fuzzy Matter Element

WANG Yong,WU Li-xia,CAI Ming
(School of Traffic&Transportation,Chongqing Jiaotong University,Chongqing 400074,China)

In order to solve issues of quantization of qualitative indexes and scope definition of hierarchical values in the rail transit operation safety evaluation process,an evaluation model which combined entropy weight(EW)with fuzzy matter-element(FME)to evaluate rail transit operation safety indicators was established.It was based on fuzzy matter-element model by introducing entropy method to finalize index weight and selecting the idea of Euclid approach degree to reflect the extent of closeness between the unvalued safety results and standard safety results.On the basis of previous studies,indexes of urban rail transit operation safety evaluation system were divided into four levels,including excellent,good, fair,and bad.Besides,the range of each level was also provided.Taking Chongqing rail transit Line 3 as an example,compared to method of extension matter-element(EME),the EW-FME model were analyzed.The results showed that the EW-FME model evaluation index was 0.5889 and the EME level of risk evaluation was 3,which both reached to the degree of good safety.The study indicates that EWFME model can solve the problem of non-quantitative evaluation effectively.The precision of evaluation is further improved in comparison with EME model.

rail transit;safety assessment;fuzzy matter-element model;entropy weight;Euclid approach degree

U491.5

A

2095-9931（2015）06-0051-07

10.16503/j.cnki.2095-9931.2015.06.009

2015-06-23

汪勇（1992—），男，安徽芜湖人，硕士研究生，研究方向为交通运输规划与管理。E-mail：liucao138@163.com。