信息化条件下CDM交通分布模型修正与验证

李春燕，叶晓飞，陈 峻，孙正安

（1.深圳市综合交通运行指挥中心，广东 深圳 518041；2.宁波大学 海运学院，浙江 宁波 315211；3.东南大学 交通学院，江苏 南京 210096；4.深圳市城市交通规划设计研究中心，广东 深圳 518021）

信息化条件下CDM交通分布模型修正与验证

李春燕1，叶晓飞2，陈 峻3，孙正安4

（1.深圳市综合交通运行指挥中心，广东 深圳 518041；2.宁波大学 海运学院，浙江 宁波 315211；3.东南大学 交通学院，江苏 南京 210096；4.深圳市城市交通规划设计研究中心，广东 深圳 518021）

为了研究信息化条件下交通出行分布规律，以基于最大熵理论的目的地竞争力分布模型（CDM）为研究对象，从出行者对目的地选择行为这一微观角度出发，引入目的地强迫度和信息强迫度两个参量，对CDM进行修正。通过建立无信息和有信息两种假设情景，以弹性出行和非弹性出行两种出行目的为分类，分析出行者对不同类型出行目的地的选择过程，建立最大熵优化模型，通过求解引入新参量后的多目标优化问题，建立CDM交通分布修正模型并进行参数估计。利用南京市居民出行调查数据对CDM修正模型进行验证，并与传统的双约束模型进行对比，结果显示CDM修正模型拟合误差在2%以内，精度较高。改进后的CDM修正模型不仅能够减小拟合误差，而且能够体现出行目的地的选择行为对交通分布的影响程度，在信息化条件下能够很好地模拟居民出行分布规律。

城市交通；信息化条件；交通分布；最大熵；CDM修正

0 引言

交通出行分布预测是城市交通规划的一个重要环节，传统条件下交通分布预测以宏观集计模型为主，主要包括增长系数法和重力模型两种。由于交通分布受交通阻抗的影响较大，相对于增长系数法，重力模型能够更好地描述这一特征。在信息化条件下，每个出行者的个体出行行为都会因接收到的信息不同而发生较大变化，需要从微观个体特征出发，通过分析个体出行目的特征，得到以个人为单位的交通分布情况，从而集计得知宏观上的交通分布情况。可见，信息对交通分布有很大的影响。传统条件下的交通分布模型在处理以个体为单位的微观交通出行行为方面尚存在不足，需要加以修正。国际上，Wilson A.G.[1]在1967年评述了熵的基本原理，并利用最大熵原理对重力模型给出了理论证明，这为揭示重力模型的本质和模型修正提供了依据和思路。Abdel-Aal M.M.M.[2]以埃及亚历山大省各城区之间的通勤交通出行分布为例，通过对双约束重力模型进行修正，对每种出行目的地对应的出行分布模式均有较好地模拟和体现，该模型还可以考虑应用到弹性出行目的下的交通分布研究；Antoniou C.等[3]从状态和空间两个角度对传统的OD预测模型进行扩展，使其能够利用信息化条件下不同渠道获取的交通数据进行交通预测；Chang C.P.等[4]依托美国橡树岭国家实验室开展信息化条件下实时交通出行预测和离线规划系统的开发与应用，通过该系统可以对出行者的交通出行决策进行影响分析。国内对最大熵模型的研究主要集中于应用层面，其中谭明军[5]将最大熵模型应用到交通枢纽的换乘量分布预测中，为综合客运枢纽的规划建设提供了科学依据；邵昀泓等[6]从宏观上描述了出行者的交通出行行为特征，同时针对最大熵模型在交通分布中的应用展开讨论，发现最大熵模型比常用的双约束重力模型适应性更强；常玉林等[7]将最大熵模型应用到公共交通分布预测中，以乘客公交出行距离为约束条件，将对应状态数最多的出行分布作为预测的出行分布，提出改进后的熵模型参数标定方法，发现改进后的模型在公共交通分布预测中有很好的应用前景。

综合以上文献可以发现，目前国内研究主要集中于对交通出行分布传统模型的应用层面，国外研究主要集中于对修正模型的具体案例应用层面。为适应日趋复杂的交通信息环境，本文将以目的地竞争力分布模型（Competing Destinations Model,CDM）为例，在阐述CDM发展的同时，针对其部分缺陷，采用最大熵原理，从体现信息影响过程和信息影响结果两个角度对修正模型加以推导，并采用具体实例进行计算，对该修正模型的合理性进行验证。

1 CDM简介

竞争就是利用某种优势，在资源有限的前提下，通过相互作用，获取生存和发展的优越机会，在时间和空间上选择、劣汰和发展的过程。目的地竞争就是出行目的地利用本身的区位优势竞争，培育各自的腹地、市场和影响区，形成空间集聚和中心化，从而对出行者产生足够的吸引强度，诱使出行者出行[8]。由于城市交通分布规律与出行目的地关系密不可分，运用目的地竞争原理，可以解释出行者在城市不同空间、不同尺度和不同类型中的自组织演化，从而描述不同出行目的的交通分布情况。由Fotheringham教授在20世纪80年代提出的目的地竞争力分布模型（Competing Destinations Model，CDM）是重力模型的一种，其在目的地竞争原理的基础上，详细阐释并展现了与交通分布相关的出行距离的凝聚性和竞争性两个特性，很好地描述了出行交通分布规律，已经在旅游、经济等多个研究领域得到应用[9-10]。CDM是对传统条件下重力模型的修正，其基本形式为：

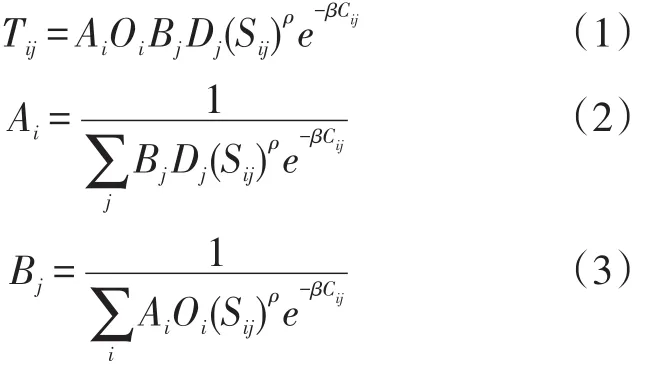
式（1）～式（3）中：Tij为i,j小区之间的交通出行分布量；Ai,Bj为模型参数；Oi为i小区的交通产生量；Dj为j小区的交通吸引量；Cij为i，j小区之间的出行阻抗；β为出行阻抗参数；ρ为两小区之间阻抗函数的凝聚性或者竞争性；Sij为j小区相对于其他各个小区对i小区的吸引强度，用式（4）或式（5）定义：

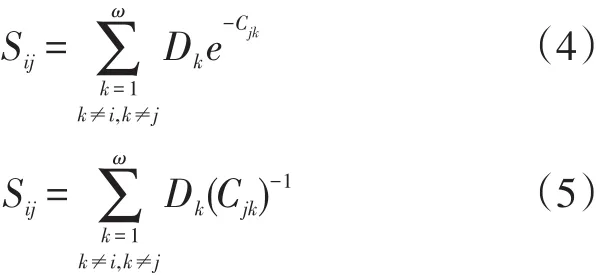
式（4）和式（5）中：ω为小区总数；Dk为第k个小区的交通吸引量；Cjk为j小区与k小区之间的出行阻抗。

式（2）和式（3）中，ρ的标定分以下两种情况。

①当两小区之间的阻抗增大时，其出行分布量会减少，称这一特性为两小区之间阻抗函数的凝聚性，此时ρ＞0；

②当出行者意愿出行的距离增大时，其可选的目的地增多，因此具有较高的出行满意度，称这一特性为两小区之间阻抗函数的竞争性，此时ρ＜0。

式（1）可通过对以下最大熵多目标的优化得以求解：

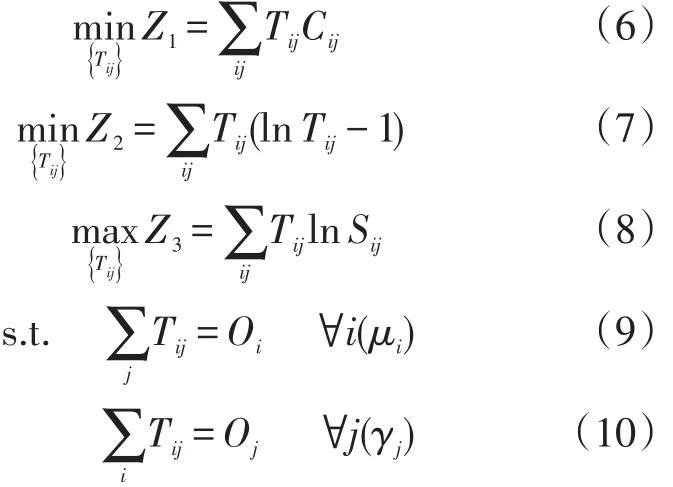
其中，式（6）～式（8）式为目标函数；式（9）～式（10）为约束函数；Z1，Z2，Z3为目标函数值；Tij,Cij,Sij,Oi含义同式（1）～式（3）；Oj为j小区的交通产生量；μi为所有i小区的集合；γj为所有j小区的集合。

与双约束重力模型相比，CDM增加了Sij这一参量，优化目标函数通过增加式（8），从i,j小区之间可达性的角度间接表达了出行者行为对交通分布的影响。不过，CDM有两个重要的缺点：其一是式（4）和式（5）只从宏观角度考虑了出行阻抗对i,j两小区间可达程度的影响，从微观个体角度看不够全面，事实上每个出行者的交通分布情况不仅仅取决于出行距离、出行费用、出行时间等出行阻抗因素，当面临不同出行目的时，其目的地的吸引程度均有所不同；其二是从式（1）～式（5）可以看出，出行者接收到信息时的不同反应对分布的影响没有得到体现。当出行者接收到不同出行信息时，由于其出行目的的差别，信息可能会使得出行者改变目的地或者取消出行。从以上两种微观角度出发，式（4）和式（5）亟需改进。

2 CDM模型修正

2.1 修正思路

基于以下三个假设条件：①用以同一弹性出行目的的小区有N（N≥2）个可供出行者n选择；②出行者在出行过程中不会改变目的地；③提供给出行者的信息指出行前信息。本文以出行个体为研究对象，考虑以下两种情景。

情景一：没有提供信息的情况下出行者的交通分布规律。此时，出行者n根据其出行目的和出行目的的起讫点i,j的交通阻抗综合考虑目的地地址，式（3）主要将交通阻抗（为方便实例验证，本文统一采用i与j小区之间的出行时间tij表示）作为两小区之间的可达性参量，但实际由于出行目的的不同，有时即使tij很大，出行者依然选择原小区作为目的地。因此本文引入j小区对出行者的强迫度参量λ1作为另一主要影响因素，并且定义λ1由出行目的决定，为加强对比，选择典型的弹性出行和非弹性（上班）出行两种出行目的，取值如表1所示。

表1 不同出行目的λ1取值

情景二：当居民接收到新的信息后，该信息会对出行者作出的原目的地选择决定产生影响，设其影响程度用λ2表示，并根据信息的不同种类，分别令λ2=1（提供的信息不利于出行者到达该目的地）和0（提供的信息有利于出行者到达该目的地），在tij,λ1,λ2的综合影响下，出行者n会作出最终目的地选择决定。

2.2 修正模型建立

将tij,λ1,λ2对出行者n的目的地选择影响采用指数分布的形式来表达，则选择j小区对i小区所有出行者的吸引度（ωij）可采用Hansen定义[11]表达如下：

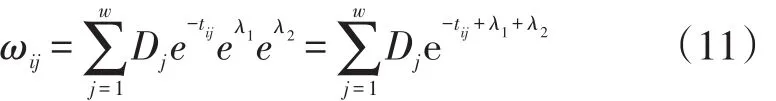
式（11）中：ωij为修正后j小区相对于其他各个小区对i小区的吸引强度；Dj含义同式（1），为j小区的交通吸引量；tij为i小区与j小区之间的出行时间；λ1为j小区对出行者的强迫度；λ2为居民接收到的新信息对出行者作出的原目的地选择决定的影响程度。

将式（8）变换为式（12），求解由式（6）、（7）、（12）构成的目标函数以及由式（9）、（10）构成约束条件的多目标优化问题，得到CDM修正模型如式（13）～式（15）所示。

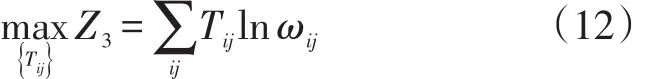
式（12）中：Z3为修正后的目标函数；Tij含义同式（1）；ωij含义同式（11）。

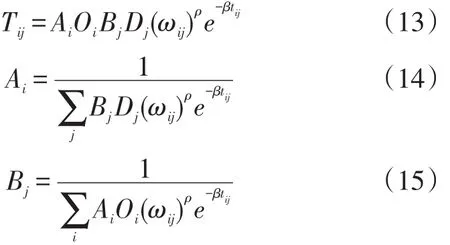
式（13）～式（15）中：Tij,Ai,Bj,Oi,Dj,β,ρ含义同式（1）；ωij含义同式（11）。

比较式（3）、式（4）与式（11）可以看出，式（3）与式（4）中Sij着重强调i,j小区之间的交通分布与其他各个小区之间的分布都有关系，并且这种相关性主要通过交通阻抗体现，式（11）的形式与式（3）、式（4）类似，但认为ωij主要由j小区的吸引量决定，并且受到交通阻抗、出行目的和信息的综合影响。从实际意义上讲，式（11）除反映了多个影响交通分布的因素外，还体现了出行者的出行行为变化，因为城市居民在进行某一目的的出行时，根据其经验已经存在一个目的地地址，并非对所有小区进行一一比较后再进行选择，因此式（11）更具有实践意义。

从式（13）～式（15）中可以看出，当ρ=0时，CDM修正模型转变成双约束模型一般式，体现了当j小区对i小区的吸引度为0时，两小区之间的交通分布主要受到交通阻抗的影响；当ρ≠0时，交通阻抗并非是影响小区交通分布的唯一因素，这与在实际出行过程中，出行者考虑影响因素的过程也是相符的。

2.3 修正模型的参数估计

利用最大似然法对CDM修正模型中的β，ρ进行估计。设出行者接受信息后的出行分布概率可表示为：

式（16）中：Pij表示i小区与j小区之间的出行分布概率；Tij意义同式（1）。

建立式（16）的似然函数：

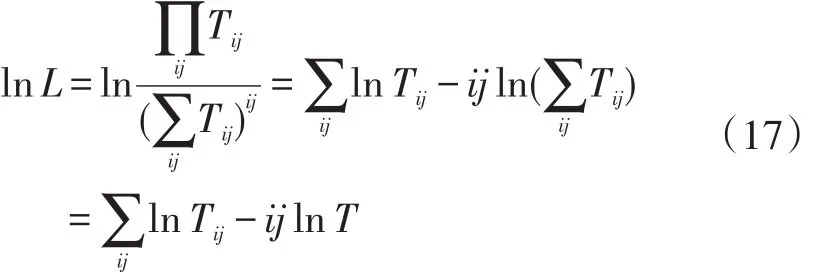
式（17）中：L为似然函数；Tij含义同式（1）；T为各小区之间交通出行总量。

将式（13）代入式（17），并进一步简化得到CDM修正模型中β，ρ的似然函数：

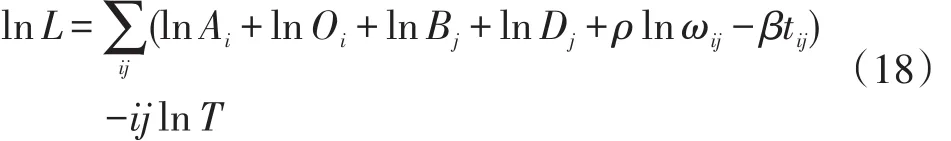
式（18）中：Ai,Bj,Oi,Dj,β,ρ含义同式（1），T含义同式（17）；ωij含义同式（11）。

当各参量已知时，对上式分别计算β,ρ的偏导数，求解由各参数所组成的非线性方程以得到修正模型中的参数[12-13]。

3 修正模型验证

3.1 数据采集

为研究以上修正模型的合理性，以2009年南京市居民出行调查结果为数据源开展验证工作。调查者的出发地和目的地均分布在图1所示的5个交通大区内，图中各大区之间的出行时间数据为阻抗tij。本文对南京市出行者在信息化条件下不同出行目的地的选择行为做RP（Revealed Preference，显示性偏好）调查和SP（Stated Preference，陈述性偏好）调查。

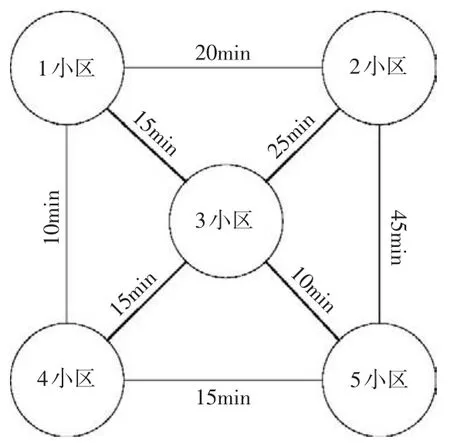
图1 计算示例图

本次调查中，向被调查者提供“今天天气较差，会有大雨”的信息，由被调查者分别回答当出行目的分别为上班和购物时其出行目的地的改变和选择情况。剔除由调查选择项不全等因素造成的无效样本，本次调查共获得875 721份非弹性（上班）出行目的有效样本，732 773份弹性（购物）出行目的有效样本。被调查者在不利信息条件下对两种出行目的地改变情况如表2所示。

表2 信息条件下弹性和非弹性出行目的地改变比例表

从表2中可以看出，不利实时信息的发布对出行者目的地的改变有较大影响，尤其是对弹性出行目的，当出行者接收到会有大雨的信息时，86%的出行者会因为距离太长而改变出行目的地，从而换为较近目的地进行购物，相比而言非弹性出行者所受影响较小，95%出行者仍然会选择上班。

将被调查者的出行目的按照非弹性（上班）和弹性（购物）两类进行分类，被调查者在得到以上信息后各小区之间的OD分布如表3和表4所示。

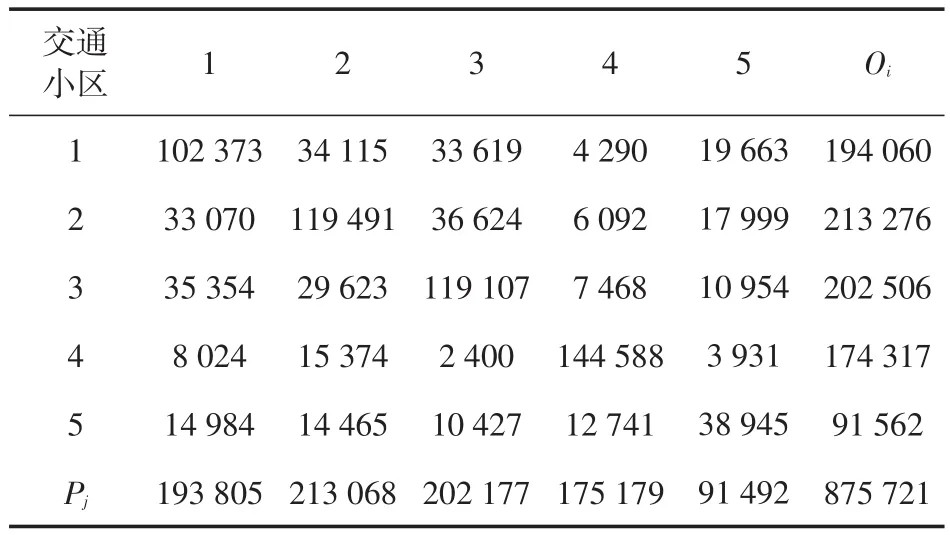
表3 非弹性（上班）目的的交通小区发生吸引量及OD分布（单位：人次）

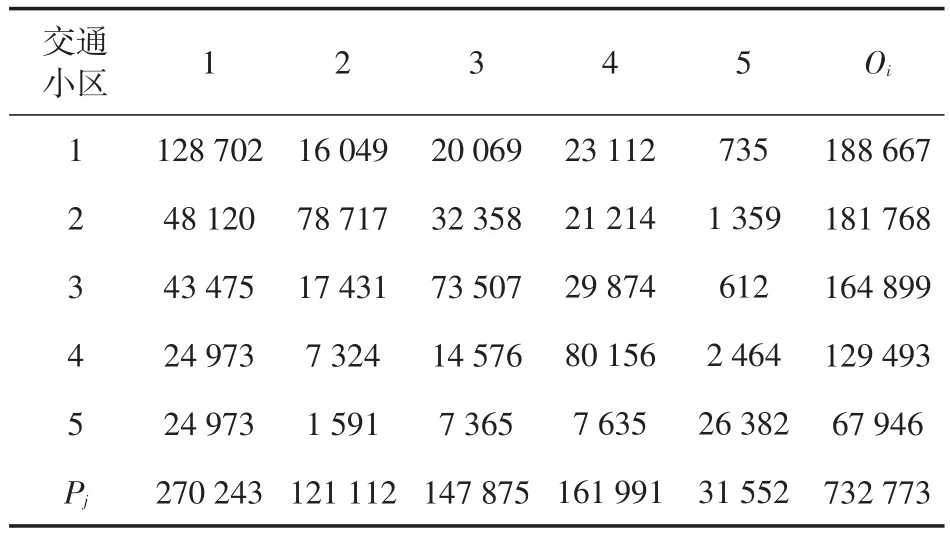
表4 弹性（购物）目的的交通小区发生吸引量及OD分布（单位：人次）

3.2 模型修正结果

采用各小区之间的交通流量OD分布数据求得CDM修正模型中的β=0.376,ρ=0.414，利用CDM修正模型和双约束重力模型对各小区之间的交通分布进行拟合，得到交通分布拟合误差如图2和图3所示。

综合比较图2和图3可以发现以下几点。

（1）采用双约束重力模型和CDM修正模型对现状的交通分布拟合误差均控制在2%以内，拟合结果较好，但总体而言CDM修正模型的拟合结果明显优于双约束重力模型，尤其体现在对以弹性出行为目的的交通分布中。综合观察两个图可以发现，双约束重力模型对所有形式的区内交通分布拟合误差都较大，且误差值均为正，说明双约束重力模型在预测区内出行时，结果偏大现象较严重，相比而言修正模型对区内交通预测结果优于双约束重力模型，误差偏小。

（2）双约束重力模型对以上班为出行目的的交通分布拟合误差明显小于以弹性出行为目的的交通分布拟合误差，说明CDM在拟合非弹性出行时精度更高，效果更明显。从图2中还可看出，2小区和5小区的区内非弹性交通出行预测误差比区间的预测误差略大，在拟合区内交通出行时仍存在一定误差。

（3）从图3可以看出信息对居民出行的重要影响。当出行者有条件获得相关信息时，其交通分布与仅有交通阻抗时的交通分布相比，会产生重大的变化，影响程度可以通过比较图3两种模型的误差差值得出。

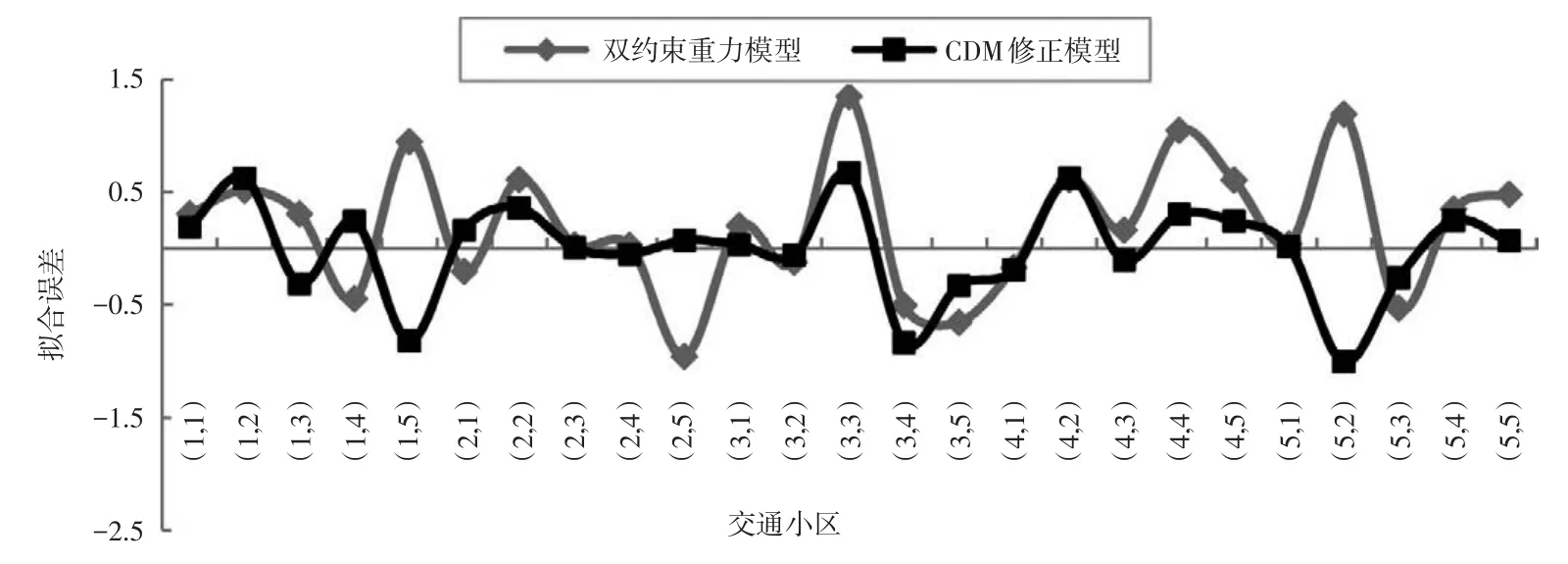
图2 CDM修正模型与双约束模型拟合交通分布误差分析——非弹性（上班）出行目的

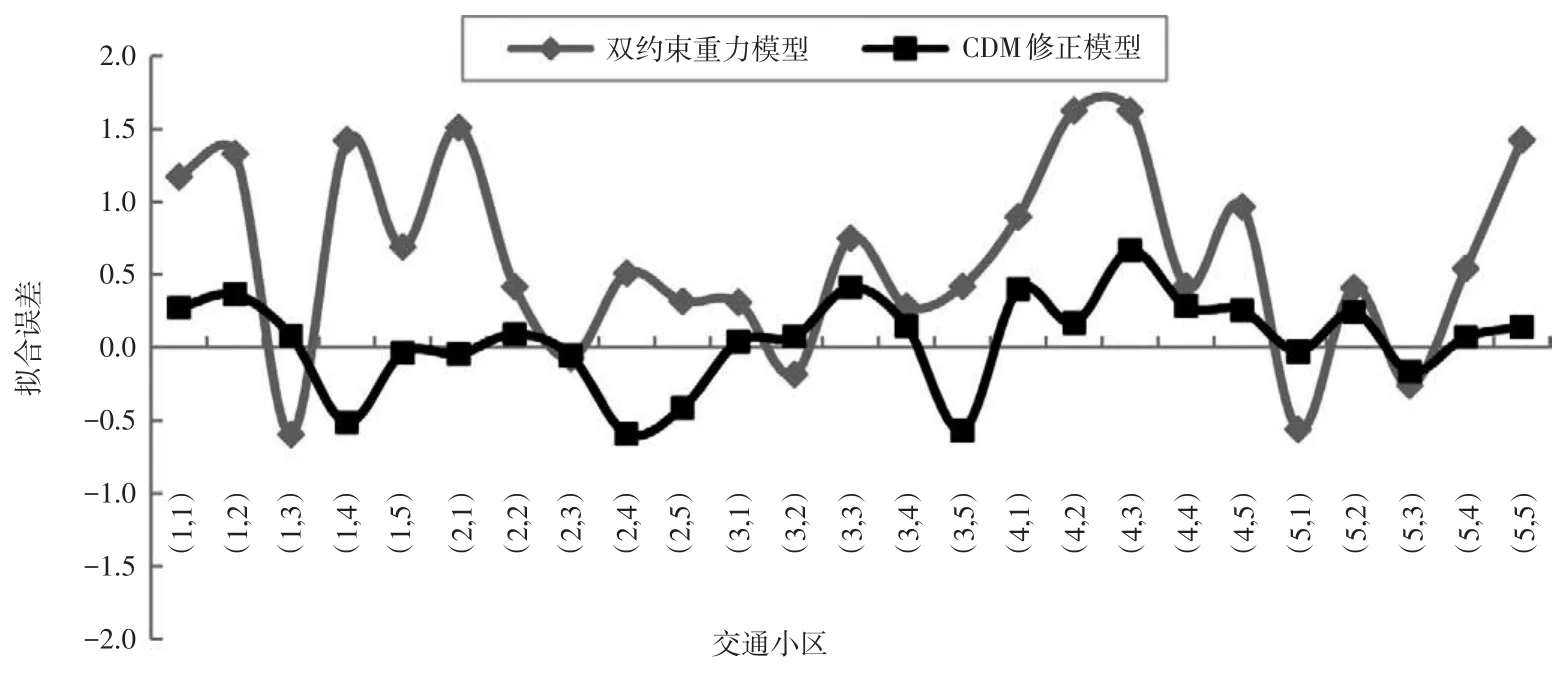
图3 CDM修正模型与双约束模型拟合交通分布误差分析——弹性（购物）出行目的

4 结语

最大熵原理能够恰当地表达物体微观状态和宏观状态之间的联系，当所考虑的优化重点不同时，通过建立能够体现该特性的目标函数，能够得出优化后不同形式的重力模型。本文通过将不同出行目的和信息影响强度对出行者的影响进行量化，优化了原目标函数，经过逻辑推导和实例验证，得出CDM修正模型具有较高的实验精度。从最后的实例看出，CDM修正模型在拟合区内交通出行时仍然存在预测误差偏大的结果，主要因为该修正模型实质仍为重力模型，有待于进一步的研究。

[1] WILSON A G.Entropy in Urban and Regional Modeling[J]. Economic Geography,1972,48(4):364-394.

[2] ABDEL-AAL M M M.Calibrating a Trip Distribution Gravity Model Stratified by the Trip Purposes for the City of Alexandria[J].Alexandria Engineering Journal,2014(53):677-689.

[3]ANTONIOU C,BEN-AKIVA M,KOUTSOPOULOS H N. Dynamic Traffic Demand Prediction Using Conventional and Emerging Data Source[J].Intelligent Transport Systems, 2006,153(1):97-104.

[4] CHANG C P.Improving Traffic Estimation and Prediction Through DynamicTrafficAssignmentDevelopment[C]// IEEE International Conference on Networking,Sensing& Control.New York:IEEE,2004:1313-1316.

[5] 谭明军.最大熵模型在福田枢纽换乘量分布预测中的应用[J].公路交通技术，2013（1）：116-119.

[6] 邵昀泓，程琳，王炜.最大熵模型在交通分布预测中的应用[J].交通运输系统工程与信息，2005（1）：83-87.

[7] 常玉林，陈向宇.最大熵模型在公共交通分布预测中的应用[J].科学技术与工程，2015（3）：285-288.

[8] FOTHERINGHAM A S.A New Set of Spatial Interaction Models:The Theory of Competing Destinations[J].Environment and Planning A,1983,15(1):15-36.

[9] MEI L,KASHIHARA S,YOSHIMURA H,et al.On the Applicability of Competing Destinations Model to the Consumer Behavior of Commercial Facilities:A Comparative Study at New Towns and an Ordinary Built-up Area[J].Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan,1996(7):181-182.

[10] Felipa De Mello-Sampayo.Competing-Destinations Gravity Model:An Application to the Geographic Distribution of FDI[J].Applied Economics,2009,41(17):2237-2253.

[11] ERLANDER S,STEWART N F.The Gravity Model in TransportationAnalysis[M].Netherlands:VSPUtrecht,1990.

[12] JOHN R R.Spatial Interaction Modeling[J].Regional Science.2004(83):339-361.

[13] 盛昭瀚，曹忻.最优化方法基本教程[M].南京：东南大学出版社，1990.

Modification and Validation of CDM Trip Distribution Model Under Information Condition

LI Chun-yan1,YE Xiao-fei2,CHEN Jun3,SUN Zheng-an4
(1.Shenzhen Transportation Operation Command Center,Shenzhen 518041,China;2.School of Maritime and Transportation,Ningbo University,Ningbo 315211,China;3.School of Transportation,Southeast University, Nanjing 210096,China;4.Shenzhen Urban Transport Planning Center,Shenzhen 518021,China)

In order to study trip distribution under information condition,a competing destinations model based on maximum entropy theory was taken as the research objective.From the microcosmic standpoint of travelers′destination choice behavior,the CDM was modified based on two new introduced parameters,which were trip destination forcing factor and information effecting degree.Two hypothetical scenarios with and without information were established,compulsory trip destination and non-compulsory trip destination were classified,travelers′choice process of different trip destinations were analyzed and the maximum entropy model was founded.The multi-objective optimization problem with new introduced parameters was solved,the modified CDM trip distribution model was founded and parameters were estimated.The modified CDM was verified by using the resident trip survey data in Nanjing andwas compared to the doubly constrained distribution model.The result shows that the fitting error of the modified CDM is under 2%and much more precise.The modified CDM not only decreases the fitting error but also reflects the impact of travelers′destination choice behaviors on trip distribution.It is suitable for describing trip distribution under information condition.

urban traffic;information condition;trip distribution;maximum entropy;CDM(Competing Destinations Model)modification

U491.1

A

2095-9931（2015）06-0058-06

10.16503/j.cnki.2095-9931.2015.06.010

2015-10-19

国家高技术研究发展计划（863计划）项目（2011AA110304）；国家自然科学基金项目（51408322）

李春燕（1986—），女，山东临沂人，工程师，博士，主要研究方向为交通规划与管理、智能交通。E-mail：duoduo.mu@foxmail.com。