整体思考的优越性——以20以内的进位加和退位减为例

胡重光，杨高全

（湖南第一师范学院，湖南长沙410205）

整体思考的优越性
——以20以内的进位加和退位减为例

胡重光，杨高全

（湖南第一师范学院，湖南长沙410205）

学得多比学得少有时候更容易，这看起来是矛盾的，却是教学的辩证法。辩证法的一个基本观点是，事物是普遍联系的，事物的发展变化是有规律的。小学数学中也普遍体现了这一点，20以内的进位加和退位减就是其中的典型例子。如果整体思考，抓住其中的联系，找出其中的规律，就可以使我们的教学变得简易而有趣。用整体的观点和联系的观点思考问题，是重要的数学思维方法。

整体思考；联系的观点；20以内的进位加和退位减

学得多比学得少有时候更容易，这看起来是矛盾的，却是教学的辩证法。例如常用的公制长度单位有毫米、厘米、分米和米，如果整体学习，是非常有规律的：1米＝10分米，1分米＝10厘米，1厘米＝10毫米。并且其进率与自然数的进率相同，很容易相互类比，温故知新。如果首先抽出厘米和米两个单位来学习，就破坏了这一规律，既不易记忆，又失去了美感，也不能与记数法作类比。

辩证法的一个基本观点是，事物是普遍联系的，事物的发展变化是有规律的。小学数学中也普遍体现了这一点，20以内的进位加和退位减就是其中的典型例子。如果整体思考，抓住其中的联系，找出其中的规律，就可以使我们的教学变得简单而有趣。

这两个内容都是小学数学中的难点，为了突破难点，教材采用了“小步子、多重复”的策略，分步学习。20以内的进位加法分成9加几，8、7、6加几，5、4、3、2加几三步；20以内的退位减法分成十几减9，十几减8、7、6，十几减5、4、3、2三步。这样虽然是由易到难，稳步推进，却掩盖了其中的规律。

20以内的进位加法这一单元的“整理与复习”的第1题，要求学生写出20以内的所有进位加法算式并进行整理。题目中列出了以下的表：

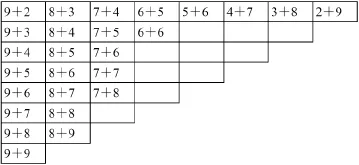
要求学生把表中的空格填满。

这张表由于只有加数没有和，就体现不出加数与和的关系。如果我们把每一个算式都填完整，情形就完全不同了：

表1 20以内的进位加法表

由于整体思考，有序排列，这张表中出现了很强的规律性：

1.所有的和都是11～18的数，因此只需确定和的个位即可；

2.9加2，和的个位是1，9加3，和的个位是2，……，9加几，和的个位就是几减1；

3.8加3，和的个位是1，8加4，和的个位是2，……，8加几，和的个位就是几减2；

4.7加几，6加几，……以此类推；

5.1是9的补数，2是8的补数……，减去的数总是第一个加数的补数。

这些规律至少可以带来两个大好处，一是便于记忆，二是能激发兴趣。

产生这些规律的原因很简单：

1.这些和中最大的是9+9＝18，最小的是9+2＝11，所以所有的和都是11～18的数；

2.用“凑10法”做这些加法，首先要从第二个加数中分出一个数与第一个加数凑成10，剩下的就是和的个位。例如8加5要先从5中分出2，与8凑成10，因此将5减去2，就得到和的个位3，而减去的数2就是8的补数。

由此我们可以对20以内的进位加的教学作出以下设计：

1.用实例引入20以内的进位加法

我国的数学课程标准（2011年版）要求培养学生的应用意识，使学生“认识到生活中蕴含着大量与数量和图形有关的问题，这些问题可以抽象成数学问题，用数学的方法加以解决。”[1]7小学数学教材也指出：“数学就在你身边。”怎样做到这一点呢？首先要求我们在学习计算前，应从生活实例中引入计算。这些实例应满足两个条件：

（1）为儿童所熟悉。有些例子虽然是生活中存在的，也具有趣味性，但是儿童很少见到，就达不到这一目的。例如小学数学教材中常常用熊猫、天鹅、企鹅、猴子等动物作例子，而这些动物儿童一般只在动物园见到，他们就感受不到“数学就在身边”。

（2）例子中的问题是儿童需要解决的。有的实例虽然就在儿童身边，但其中的问题不是儿童需要解决的，也不能激发儿童的学习动机。例如我们可以就商店卖洗衣机这一情境编一道应用题，洗衣机是儿童熟悉的，但是卖洗衣机不是儿童需要解决的问题，他们也不会感兴趣。小学数学教材中有很多这类的例子：画一幅小动物图，配上文字：左边有□只，右边有□只。一共有？只。这些小动物虽然为儿童所喜爱，但这个问题是生活中没有的，儿童不需要解决这类问题。

下面的问题则基本上能满足这两个条件：

（1）学校举行跑步比赛，小强取得第九名，小亮的名次比小强低两个，小亮得了第几名？

（2）电梯从一楼开始，先上了8层楼，接着又上了5层楼，现在电梯在第几层楼？

（3）小明今年7岁，大牛比小明大4岁，大牛今年多少岁？

（4）铅笔每盒6元，钢笔每支9元，小红要买一盒铅笔和一支钢笔，共需要多少钱？

（5）一（乙）班第一组有6名男生、5名女生，这一组共有多少名学生？

头两道题都涉及序数。序数在实践中有广泛的运用，但是教材中涉及序数的题很少。

2.让学生列出算式，并利用小棒自主计算这些题

先个人独立做，之后进行小组交流：对不同的答案进行讨论，每组确定一份最好的答案交给老师。最后，如有不同答案，教师提出来供全班同学讨论。

3.列表计算

将所有20以内的进位加法列成以下的表：

表2 20以内的进位加法算式表

让学生算出表中的每一道题，活动的过程与第二步相同。

4.找规律

出示表1，让学生找出表中的规律。先个人独立做，再将个人的发现在小组中交流。最后教师指定一组派代表向全班汇报，其他组补充。

教学结束后可将这张表贴在教室里，让学生无意中经常看到。

显然，20以内的退位减法的教学步骤与此完全类似。首先仍然要用实例引入，例如：

（1）学校举行数学比赛，小强取得11名，小亮的名次比小强高两个，小亮得了第几名？

（2）小明与小红住在同一个单元，小明住在二楼，小红住在11楼，从小明家到小红家要上几层楼？

（3）昨天的最高气温是14℃，今天的最高气温是8℃，今天的最高气温比昨天低几度？

（4）公共汽车到站时下了4人，上了12人，车上的人是多了还是少了？多了或少了几人？

（5）东东把零用钱存起来准备买一本15元的书，他已经存了9元，还差几元？

退位减法的计算比进位加法要困难些，教材介绍了两种方法。以15－9为例，一是把被减数分成10和5，用10减去9得1，再将1加5就得差是6。二是利用加减的互逆关系得出差：因为9+6＝15，所以15－9＝6。通常叫做“想加法，做减法”。

第二种方法可以使学生理解加减法之间的关系，并培养他们的逆向思维能力。计算教学不仅要让学生会算，通过计算培养思维能力更重要，因此这种方法更具有数学教育意义。美国数学教学法专家W·海敦斯教授指出：“逆运算概念是基本数学结构的一个重要概念，它对理解初等数学是必须的。”[2]154因此，选择第二种方法更有意义。

但是教学实践表明，一年级的儿童理解这种互逆关系比较困难。要突破这一难点，首先必须使儿童明白加减的互逆关系。只有明白这种关系才能学会这种算法；而只要明白了这种关系，算法就会水到渠成，顺理成章。

怎样使儿童明白这种关系呢？事实证明，靠教师讲解、画图甚至用实物演示，都收效甚微。在实践中我们认识到，必须让儿童通过主动的操作活动来领悟这一点。为此我们设计了以下两个操作活动：

活动一凑数游戏

同座二人玩，每人准备几十根小棒（或扣子、围棋子等）。首先双方约定一个要凑的数（教师要求最好是十几），比如15。然后由甲方拿出几根小棒（少于15根）摆在课桌上；再由乙方出小棒，所出小棒与桌上的小棒加起来要恰好等于15。如果出对了，那么桌上的小棒都归乙；出错了则桌上的小棒都归甲。

活动二猜数游戏

也是同座二人用小棒玩。首先拿出十几根小棒摆在桌上，接着甲从中拿走若干根，但不让乙看见是几根；然后乙要根据桌上剩下的小棒猜出甲拿走了几根。猜对了，则剩下的小棒都归乙；猜错了，就都归甲。

这两个活动取得了良好的效果，通过活动，孩子们都明白了加减法的互逆关系。这时再来做退位减法，就能顺利地按“想加法，做减法”的方法得出结果了。

那么为什么老师用各种教法都无效，采用这种让学生自己操作的活动就收到了良好效果呢？原因是这种学习方式符合儿童的认识水平和思维特点。用实物进行的操作活动是看得见、摸得着的，具体性强，而具体性越强儿童就越容易理解。小学数学的学习材料，其具体性可以分为四个水平：

1.具体水平：实物操作。例如前面两个用小棒的操作活动就属于具体水平。需要注意的是，教师用实物演示给学生看并不属于具体水平，因为在数学的认知活动中，操作过程本身起着很大的作用。

2.半具体水平：象形的图。例如小学数学教材中广泛采用的水果图、人物图等。

3.半抽象水平。图形代码或实物代码。例如画一个圆圈代表一个人，用一个小石子代表一头小鹿，等等。与半具体水平不同的是，这里的图不象形，具有更大的普遍性，因此也更抽象。

4.抽象水平：符号。例如数字、运算符号、字母等。这些材料已脱离了具体事物，完全形式化了。

根据皮亚杰的研究，小学儿童的思维处于“具体运算阶段”，所以小学数学教学应从具体水平开始，而不能用图形、演示或多媒体课件来代替学生的实物操作。小学数学教学的大量问题都是因为没有从具体水平开始教学而引起的。这一点，W·海敦斯在《美国现代小学数学》中曾多次强调。

之后学生通过计算得出了以下的表：

表3 20以内的退位减法表

让学生观察这张表，可以发现以下规律：

（1）十几减9的差比被减数的个位大1，十几减8的差比被减数的个位大2，十几减7的差比被减数的个位大3……十几减2的差比被减数的个位大8；

（2）被减数的个位加上减数的补数就得到差，例如13－6的差是3加6的补数4，即7。

这两条规律都可以用第一种计算方法来说明。掌握了这两条规律，就可以很快地写出表3中任意一道减法的差。

这些规律为20以内的退位减法提供了一种迅速、准确，普遍适用又简单易记的求差方法。这一方法是依靠把所有20以内的退位减法按一定的顺序排列起来而发现的，如果我们单个地或分开来教学，就不容易看出其中的规律。其实，用整体的观点和联系的观点思考问题，是重要的数学思维方法。

综合以上的教学实践和理论分析可知，20以内的退位减法应按以下步骤来教学：

1.由实例引入20以内的退位减法。

2.通过前面的活动一和活动二，学习用“想加法，做减法”的方法计算20以内的退位减法。

3.列出20以内的所有退位减法，排列成有序的表，得出前面的表1。

4.用“想加法，做减法”的方法计算出表1的所有减法，填上差，得到表2。

5.观察表2，找出其中的规律。运用第二种算法讨论、分析为什么会有这样的规律，得出计算20以内的退位减法的简便算法。

6.进行多种形式的巩固练习。

按这样的步骤教学，既能培养学生快速、准确的计算能力，又能使他们理解加减运算的互逆关系，从而发展逆向思维能力；通过观察数表找规律还能培养观察能力。因此能较好地实现知识学习和能力培养相结合的新课程教学目标。

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012.

[2][美]W·海敦斯.美国现代小学数学[M].程子明，等.译.上海：华东师范大学出版社，1989.

On the Advantage of Integrated Thinking:A Case Study on Addition and Subtraction with Carry within 20

HU Chong-guang,YANG Gao-quan
(Hunan First Normal University,Changsha,Hunan 410205)

Sometimes learning more is easier than learning less,which seems to be contradictory,but embodies the dialectics of teaching.A basic view of dialectics is that all the things are interrelated and the development of things has rules,which can also be seen in primary math teaching.The addition and subtraction with carry within 20 is a typical example.Making use of integrated thinking,grasping the inner relation in it and finding the rules can make the teaching will be easy and interesting.Thinking about questions with integrated and related thinking is a key way of thinking for math.

integrated thinking;view of relation;addition and subtraction with carry within 20

G623.5

A

1674-831X（2015）02-0001-04

[责任编辑：胡伟]

2014-12-15

湖南省教育科学规划课题（XJK013CJC004）;湖南省省级重点建设学科“课程与教学论”建设项目资助

胡重光（1950-），男，湖南道县人，湖南第一师范学院教授，主要从事数学教育研究；杨高全（1958-），男，湖南华容人，湖南第一师范学院教授。