输电导线间距计算与三维可视化
2015-12-15王洪申张任俊张林
王洪申,张任俊,张林
(1.兰州理工大学机电工程学院 ,甘肃 兰州 730050;2.甘肃省制造业信息化工程技术研究中心,甘肃 兰州 730050)
0 引言
输电线路设计时,一定档距和弧垂下,如果导线之间距离较小,在大风或脱冰舞动工况下,可能会引起相间闪络,从而导致跳闸故障。为了线路安全运行,导线之间应满足一定的距离要求,需要对导线间最短距离进行验算。导线间距离是三维空间悬链线间距离,计算量很大,容易出现如果用人工验算将浪费大量的时间和人力,严重影响设计周期。目前常采用的解决方法是将各相导线简化为直线,通过近似计算或采用复杂的启发式算法来求解[1-3],这样计算结果往往会产生较大的误差。本文给出一种利用计算机实现空间悬链线间距离验算的方案,采用BBD-Tree数据结构,并用近似最近点搜索算法计算导线之间的最小间距以及所对应的悬链线上的点。最后运用三维可视化技术将计算结果直观地进行三维显示,从视觉上辅助验证计算结果的可靠性。
1 实现原理
1.1 坐标系的建立与参数输入
以两杆塔轴线之间的连线为y轴,垂直于水平面的方向为z轴,并根据右手定则确定x轴的方向。依据定好的坐标系确定出两杆塔上具有连接关系的各点的坐标值,再输入其他的相关参数如张力、荷载等,从而完成导线间距计算中所需要的各项参数的输入。
1.2 二维空间中悬链线数据点的计算
设一条导线起点为 A1(x1,y1,z1),终点为 A2(x2,y2,z2),设想将导线所形成的悬链线A1A2平移到 OA',再将OA'旋转到OA,使OA在YOZ平面上(如图1所示)。用文献[4]中给出的悬链线公式,将坐标原点设在O点,在二维空间YOZ上计算悬链线OA的各坐标点(如图2所示)。所用的公式如下:
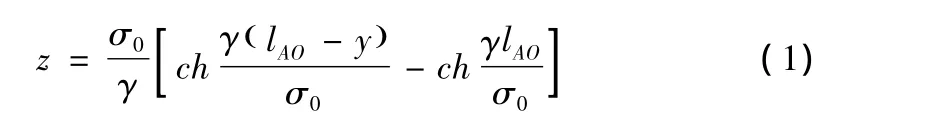
σ0——电线各点的水平应力,单位为:N/mm2
γ——电线比载,单位为:N/(m·mm2)
l——档距(两悬挂点之间的水平距离),单位:m;
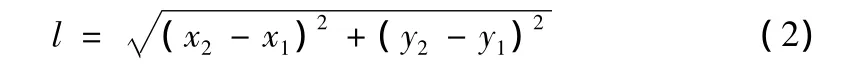
h——高差(两悬挂点之间的垂直距离),单位:m;
1.3 悬链线上二维数据点向三维空间的转化
通过1.2节计算,得到的各条导线的数据为二维空间YOZ上的点,将这些二维点表达成三维空间齐次坐标形式为[x y z
1],其中 x=0。实际应用中,导线所形成的悬链线之间通常是空间位置关系,因此,还需要通过旋转平移矩阵M将每条线上的各点变换成空间三维的坐标点:

图1 悬链线在二维空间和三维空间之间的转化

图2 在YOZ二维空间计算悬链线上的各坐标点

θ的含义见图 1,Δx=x1;Δy=y1;Δz=z1。
1.4 导线间最短距离的计算和档中距离的计算
1.4.1 导线间最短距离的计算
当导线为水平排列时,水平线间距离的要求值的计算用如下公式[5](适用于1 000 m以下档距):

其中:ki——悬垂绝缘子串系数,见表1;D——导线水平线间距离,单位:m;Lk——悬垂绝缘子串长度,单位 m;U——输电线路标称电压,单位:kV;fx——对应点导线最大弧垂,单位:m。
如果相比较的两条输电线的对应点弧垂值不相等,则取较大的弧垂作为fx的值。

表1 ki系数
为了计算两条导线的最近距离,可以采用两层循环计算两条悬链线上的各点间相互距离(复杂度为O(n2)),找出所有对应点中距离最小值和该值所对应的两条线上的坐标点。由于在计算悬链线各点坐标时,将悬链线进行了离散化处理,因此计算两悬链线间最短距离时会有一定的误差。在计算中为了提高计算精度(缩小计算误差),可以适当缩小“计算步长”,但步长越小,计算所需时间和空间增加很快,为此,本文采用BBD-Tree数据结构,并用近似最近点搜索算法[6]计算导线之间的最小间距以及所对应的悬链线上的点,使算法的复杂度O(nlogn),有效地提高算法的执行效率。
设两条导线(悬链线)分别为L1和L2,计算L1与L2之间的最短距离算法伪代码描述:
构造L2上各点的BBD-Tree数据结构;
设最短距离变量Lmin=∞;
For(L1上的每个离散点qi)
{
利用3.2.1中的算法在L2上各点所建立的BBD-Tree中搜索qi的近似最近点pi,得到的最近距离dist(qi,pi);
If(Lmin> dist(qi,pi))Then{使 Lmin=dist(qi,pi);记录 L1和L2上对应的点;}
}
输出导线L1和L2之间的最短距离Lmin和该距离所对应的两条导线上的三维点。
计算出空间两条导线的最短距离后,为了用最短距离和要求值进行比较,需要将两条导线的空间距离转化为等效水平线间距离,按如下公式计算:

其中Dx——导线等效水平线间距离,单位:m;Dp——导线间水平投影距离,单位:m;Dz——导线间垂直投影距离,单位:m。
比较DX与D的值,得出结论。当Dx≥D时,则导线间距合格;当Dx<D时,表明导线间距不合格,需要重新设计调整。
1.4.2 导线档中距离的计算
导线在档中处往往具有最大的弧垂,因此验证档中处导线间距具有一定的实用意义。先找出两条导线中档中弧垂最大的导线,找到该导线档中点的y坐标ym,再找到另一条输电线上y=ym点的坐标。计算两点间距离,然后用公式(7)和公式(8)计算要求距离和等效距离,从而验证导线档中间距的可行性。

图3 输电线路最短距离计算结果
2 输电线路的三维可视化
采用VC-2005为开发环境,以开源软件包VTK[7](Visualization Toolkit)为三维可视化工具,实现导线间距计算结果三维可视化。为提高可视化视觉效果,可将悬链线上各点的x、y、z坐标进行适当地缩放。为了使导线的显示更加美观光滑,采用样条插值的方法对导线进行造型。
3 运行验证
以计算三相导线之间的间距来验证本文提出的解决方案,三相导线为:A1A2、B1B2、C1C2,它们的坐标分别为:A1(2,0,0)、A2(-3,350,6);B1(5,0,3)、B2(0,400,6);C1(6,0,15)、C2(5,500,6),各坐标的单位用米。三条导线的水平应力取相同值σ=100 N/mm2,比载取相同值 γ=0.028 N/m · mm2。悬垂绝缘子串系数ki=0.4,悬垂绝缘子串长度 Lk=1 m,输电线路标称电压U=110 kV。计算结果如图3、图4所示,三维可视化结果如图5所示。本例中,计算导线间最小距离时,悬链线上取点间隔(计算步长)取1时,计算用时0.22秒;计算步长取0.1时,计算用时2.3秒,完全能够满足工程计算需要。

图4 输电线档中距离计算结果

图5 导线计算结果三维可视化
4 结束语
导线间距是线路设计中重要的控制参数。本文运用二维悬链线公式,通过坐标变换获得悬链线的三维数据,并用这些三维数据计算导线间距,得到的结果真实准确。利用开源软件包VTK,实现导线间距计算的三维可视化,在输电线路设计中具有一定的实用价值。
[1]宋金根.变电所进线档导线换位相间距离探讨[J].电力建设,1998,19(11):36-39.
[2]龚宇清,梁宁川,龚永光.架空送电线路导线电气距离的公式计算方法[J].电力建设,2009,30(7):24-27.
[3]柏晓路,葛秦岭,余雯雯,等.架空输电线路最小相间距离计算分析[J].电力科学与工程,2010,26(4):37-40.
[4]张殿生.电力工程高压送电线路设计手册[M].2版.北京:中国电力出版社,2003.
[5]110-500 kV架空送电线路设计技术规程[S].北京:中华人民共和国电力行业标准,中华人民共和国国家经济贸易委员会发布10.0.1条款.
[6]SONIL ARYA,DAVID M MOUNT,NAIHAN S NETANYAHU,et al.An optimal algorithm for approximate nearest neighbor searching fixed dimensions[J].Journal of the ACM,1998,45(6):891-923.
[7]The Visualization Toolkit(VTK).[EB/OL].(2010-12-23)[2011-01-01]http://www.vtk.org/.
