二次曲线中的定值(点)问题再探讨

●吴锋刃(杭州外国语学校浙江杭州310023)

二次曲线中的定值(点)问题再探讨

●吴锋刃(杭州外国语学校浙江杭州310023)

众所周知，在圆锥曲线中蕴含着许多几何性质，它们和谐统一，简洁明了，美轮美奂，是激发学生学习兴趣、感受数学美的好素材.在教材和练习中经常出现类似的问题:过二次曲线上一定点P0(x0，y0)的2条直线与曲线交于点P1，P2，直线P0P1和直线P0P2的斜率分别为k1和k2，当k1，k2满足k1k2=-1或k1+k2=0时，探讨直线P1P2是否过定点、斜率是否为定值.文献［1］指出:过二次曲线上一定点P0(x0，y0)的2条直线与曲线交于点P1，P2，直线P0P1和直线P0P2的斜率分别为k1和k2，当k1，k2满足k1k2=t(其中t≠0)时，直线P1P2过定点或直线P1P2的斜率为定值(并加以论证).

在这里有几个问题值得再思考:1)一般论证都比较繁琐，论证过程能否有更为统一并简化的形式?2)如果二次曲线出现xy项呢?还有类似结论吗?3)这个定值(点)的几何意义是什么?

演示1如图1，若过双曲线x2-y2=1上的点，作2条互相垂直的直线P0P1，P0P2，移动点P1并测算P1P2的斜率，发现直线P1P2的斜率为定值，这让我们直观感受到“对圆锥曲线上的定点张直角的弦恒过一定点”是一个错误结论.

图1

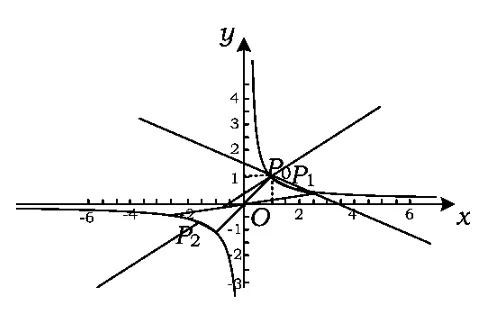
图2

演示2如图2，若过双曲线xy=1上的点P0(1，1)作2条斜率互为相反数的直线P0P1，P0P2，移动点P1并测算P1P2的斜率，发现P1P2的斜率不是定值，但P1P2过定点(0，0)，这说明“对过圆锥曲线上的定点斜率互为相反数的2条直线交圆锥曲线获得弦斜率是定值”也是一个错误结论.

下面笔者用统一的方法对此加以论证，由于探索的问题都是涉及斜率的和与积，尝试能否构造关于斜率的一元二次方程，利用韦达定理的形式加以解决呢?为了方便表达和研究，不妨先将坐标原点平移至点P0(对于定点问题，只需求出定点再反过来平移回来即可，而对于斜率来说不受平移变换的影响).一般地，可设曲线方程为Ax2+Bxy+Cy2+ Dx+Ey=0(经过原点P0)，设直线P1P2的方程为lx+my+n=0，显然直线P1P2不过点P0，故n≠0，

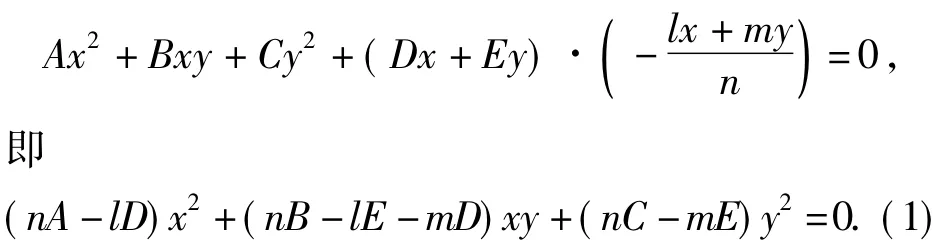
式(1)是过原点的2条直线，且点P1，P2坐标满足式(1)，故其可表示直线P0P1和直线P0P2.

设这2条直线的斜率分别为k1和k2，则k1，k2是方程

的2个根.

1)当P0P1⊥P0P2时，

此式对于任意的l，m均成立，故恒过定点

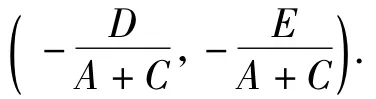
2)当k1+k2=0时，即

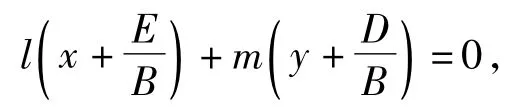
此式对于任意的l，m均成立，故恒过定点

这里，直线P1P2的斜率有它自身的几何意义.将曲线方程求导可获得曲线在点P0处切线的斜率，即将x=0，y=0代入2Ax+By+Bxy'+2Cyy'+ D+Ey'=0，即得(曲线在点P0处的切线的斜率).因此，对比后可发现:直线P1P2的斜率(定值)是点P0处切线斜率的相反数，或与点P0处切线斜率的乘积为-1(即直线P1P2与过点P0的切线互相垂直).

本文演示1即为情形1)中A+C=0的情况，演示2即为情形2)中B≠0的情况.更一般地，当k1k2=t(常数)时，

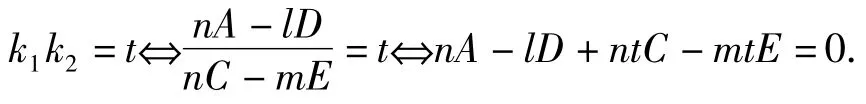
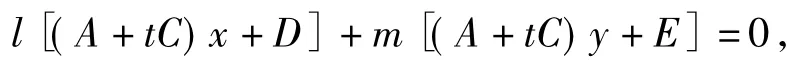
此式对于任意的l，m均成立，故恒过定点

类似地，对于k1+k2=t(常数)，利用此方法可以获得过定点和定值的结论，这里不再赘述.

［1］施开明.对一类定点(值)问题结论的修正和补充［J］.数学通报，2013(8):54-55.

［2］谢黎静.圆锥曲线中关于定点问题的再研究［J］.数学教学通讯2012(18):63-64.