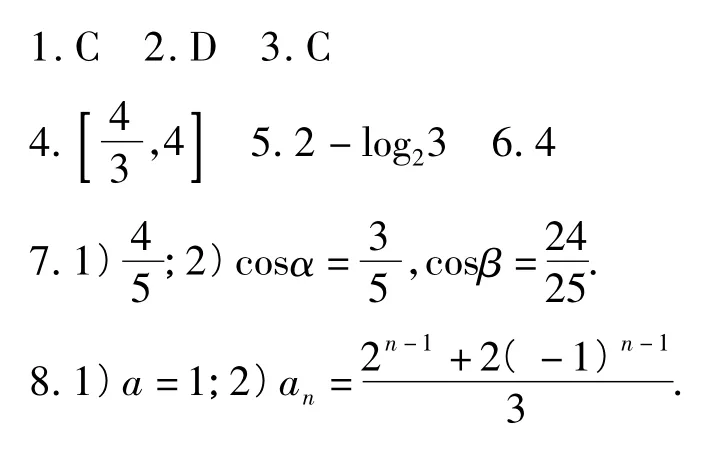化归与转化思想
2015-12-08章怡杭州第二中学浙江杭州310053
●章怡(杭州第二中学浙江杭州310053)
化归与转化思想
●章怡(杭州第二中学浙江杭州310053)
1 知识内容
数学中的化归与转化思想方法,是指在遇到具体数学问题时,通过一定的转化过程,将其归总到某类已经解决或比较容易解决的类型,然后最终解决问题的一种手段和方法.其特点是实现问题的规范化、模式化,以便通过已知的理论、方法、技巧达到问题的有效解决.
数学家波利亚强调:“我们必须一再变化它,重新叙述它,变换它,直到最后成功地找到某些有用的东西为止”,他认为解题的过程就是相互“转化”的过程:即将生疏问题转化为熟悉问题;将多元问题转化为少元问题;将复杂问题转化为简单问题;将一般问题转化为特殊问题;将一个综合问题转化为若干个基本问题.因此学生学会运用数学化归与转化的思想方法,可以有效地帮助他们实现学习上的迁移和引导,从而较快地提高日常学习质量和解决问题的能力.
2 命题分析
众所周知,数学高考命题的主要依据是数学课程标准,而命题的直接依据是数学考试大纲.在近年来的全国考试大纲以及各地的考试说明中均强调了对数学思想方法的考查,这是对数学知识在更高层次上的考查.考查时,应结合数学知识,审核考生对数学思想方法的运用能力;应从数学学科的整体上立意,注重通性通法,淡化特殊解题技巧.化归与转化思想是数学高考考查的基本数学思想方法之一.在近几年的高考数学试题中,化归与转化思想已不同程度地融入到各种类型的数学高考试题中.下面笔者以2014年部分高考试题为例,阐述一下化归与转化思想在高中数学中的应用应遵循的原则:
3 典题剖析
3.1 化生为熟的原则
解决数学问题就是将问题从一个生疏领域转化到一个熟悉领域的过程,期间注意比照已解决过的问题,找出其共性和个性.在实际解题过程中,通常表现为借鉴熟悉的事例模型,在未知问题和已知问题之间寻找转化的桥梁.
例1如图1,4个棱长为1的正方体排成一个正四棱柱,AB是一条侧棱,Pi(其中i=1,2,…,8)是上底面上其余的8个点,则(其中i=1,2,…,8)的不同值的个数为()
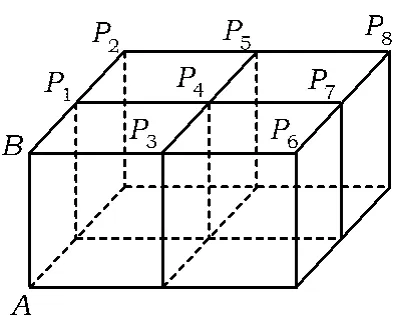
图1
A.1 B.2 C.4 D.8
(2014年上海市数学高考理科试题)
分析由正四棱柱的性质可知,AB与上底面垂直,因此AB⊥BPi(其中i=1,2,…,8),利用平面向量数量积的定义与几何意义可以发现:
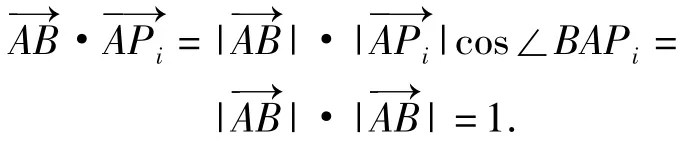
点评此题富有新意,解题的关键是充分挖掘题意隐含的条件,让学生明白在方向上的投影就是,从而将问题化归到平面向量数量积的几何意义中解题.
3.2 化多为少的原则
一个题目中往往含有较多的变量,它们之间必然存在一定的联系,我们在解题时,可以通过一定的变形和转化,来减少题目中变量的个数,从而变成一个较易解决的问题,这是一种从多元向少元的化归.
例2对于c>0,当非零实数a,b满足4a2-2ab+4b2-c=0,且使|2a+b|最大时,的最小值为.
(2014年辽宁省数学高考理科试题)
解法1(判别式法)令2a+b=t,则
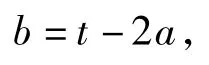
代入到4a2-2ab+4b2-c=0中,得
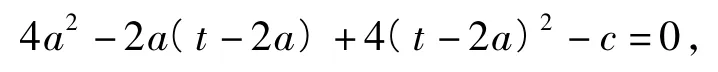
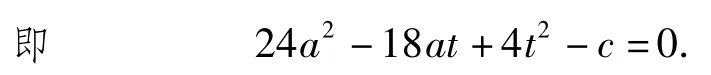
因为关于a的二次方程有实根,所以
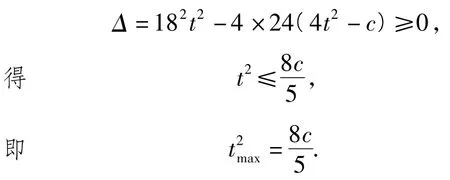
而此时由Δ=0得
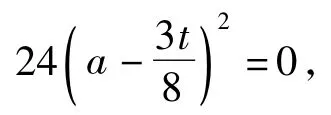
从而2a=3b,得
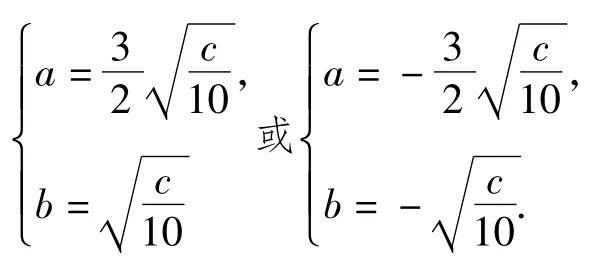
当|2a+b|取最大值时,
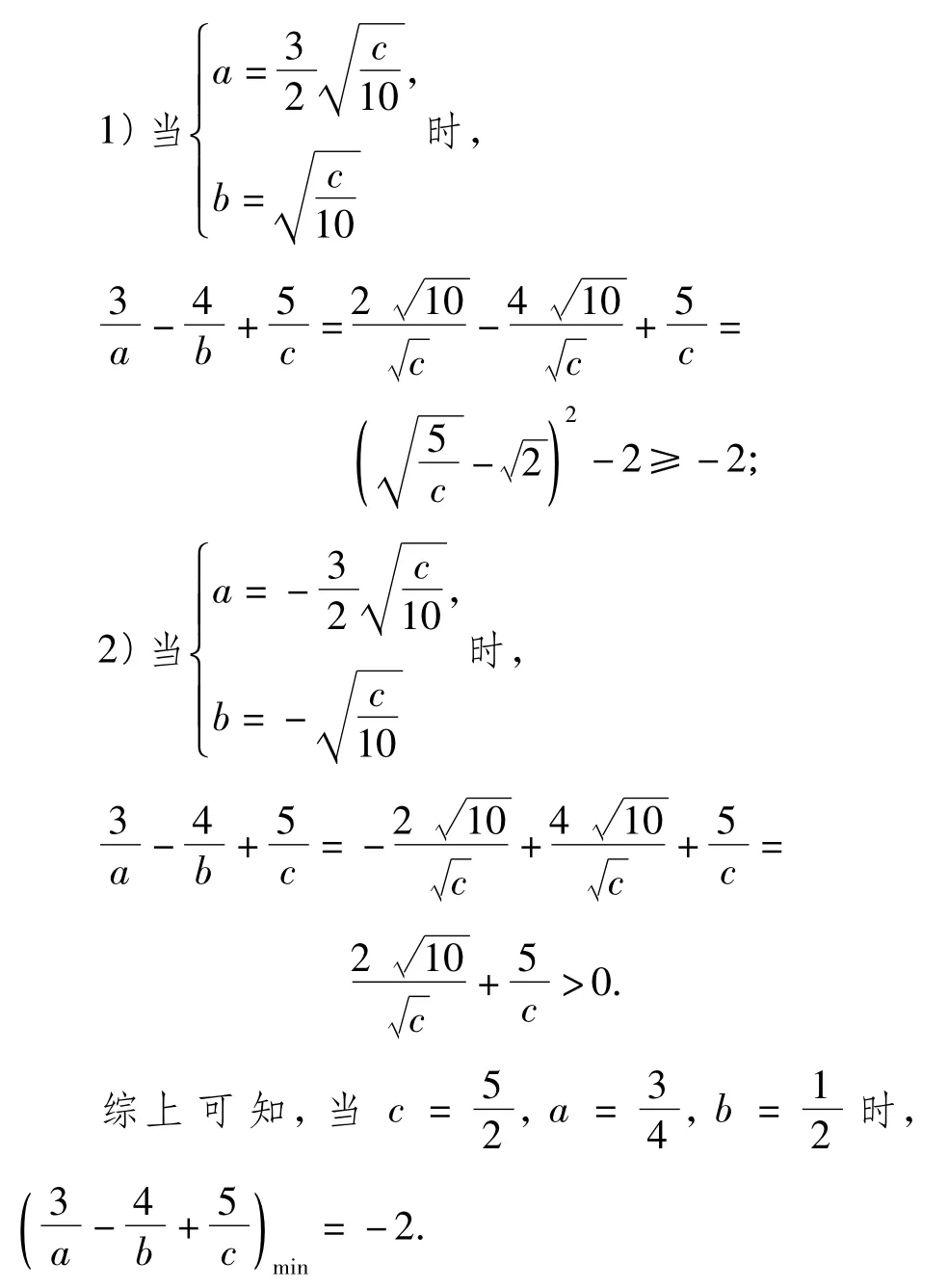
解法2(三角换元法)由已知得
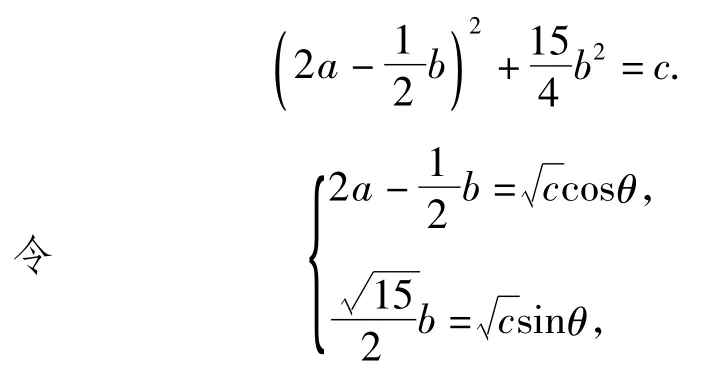


点评多元函数的最值问题一直是数学高考中检验考生思维能力和综合素质的重要素材.题中有3个变量a,b,c,而解题的目标是探讨使|2a+b|最大时,求出的最小值.因此解题过程的着重点是要放在“|2a+b|最大”上.解题中需通过从多元向少元的化归,挖掘出a,b,c这3个变量间的隐性关系.
3.3 化繁为简的原则
这一原则就是通过对一时无法解决的复杂问题,通过一定形式和方法的拆解和变形,转化为我们熟悉的简单问题,或是规范化问题,从而达到解决复杂问题的目的.
1)求椭圆C的标准方程.
2)设F为椭圆C的左焦点,T为直线x=-3上任意一点,过点F作TF的垂线交椭圆C于点P,Q.
①证明:OT平分线段PQ(其中O为坐标原点);
(2014年四川省数学高考理科试题)
分析1)由椭圆的定义可知
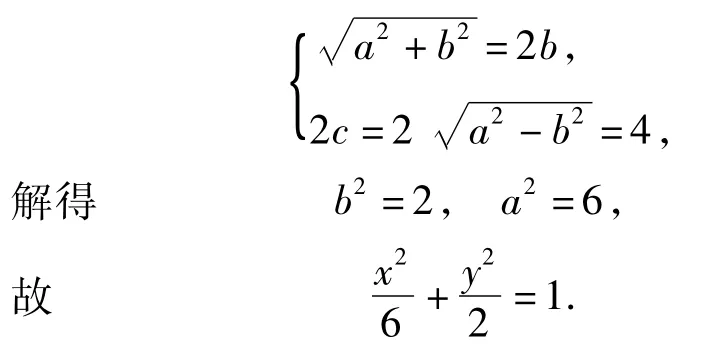
2)①要证OT平分线段PQ,可以考虑证明PQ的中点M与点O,T共线,即证
②要求2条线段比值的最值,关键是要将线段的比值转化为一个变量的函数关系式,然后再根据其类型选择恰当的方法进行求解.可以设PQ的方程为x=my-2,代入椭圆方程得到
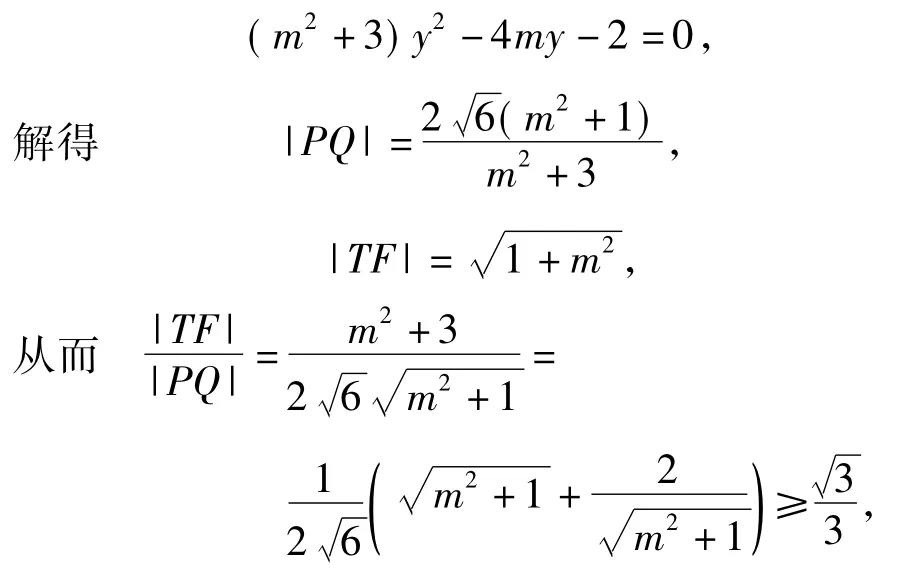
当m=±1时,取到等号,此时T的坐标为(-3,1),(-3,-1).
点评圆锥曲线的综合问题是让众多考生感到复杂而又困难的一种题型.对于此类题型在解答时要时刻关注解析几何的基本思想:用代数的方法来研究几何问题.最根本的做法就是将几何结构有系统地代数化、数量化,即先把几何问题转化为代数问题,然后运用代数的知识来解决,最后再回到几何中去.
3.4 化一般为特殊的原则
例4在平面直角坐标系xOy中,已知向量a, b,|a|=|b|=1,a·b=0,点Q满足,曲线,区域.若C∩Ω为2段分离的曲线,则()
A.1<r<R<3 B.1<r<3≤R
C.r≤1<R<3 D.1<r<3<R
(2014年安徽省数学高考理科试题)
分析设a=(1,0),b=(0,1),则
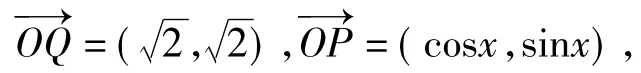
点评此题主要针对平面向量的应用与线性规划知识相结合的综合问题的考查.如按题意,对a,b设变量来做显然非常复杂,而利用特殊符合一般的原则,将a,b特殊化,较大幅度地简化了问题的难度.
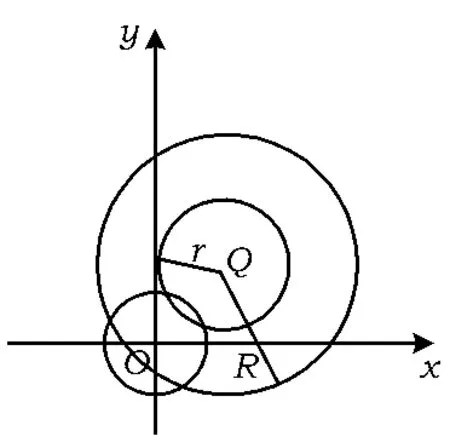
图2
3.5 化难为易的原则
例5设a1=1,(其中n∈N*).
1)若b=1,求a2,a3及数列{an}的通项公式.
2)若b=-1,问:是否存在实数c,使得a2n<c<a2n+1对所有n∈N*成立?证明你的结论.
(2014年重庆市数学高考理科试题)
分析1)由a1=1,,可猜想
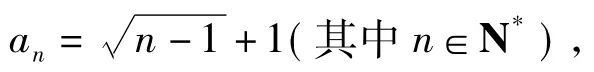
然后用数学归纳法证明这个猜想.
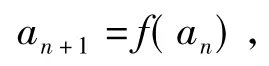
用数学归纳法证明:
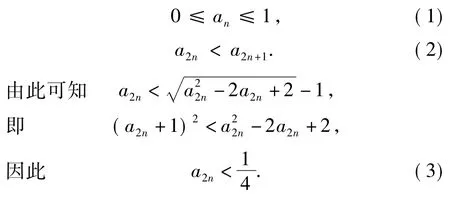
由式(1)和式(2)及f(x)在(-∞,1]上为减函数,得
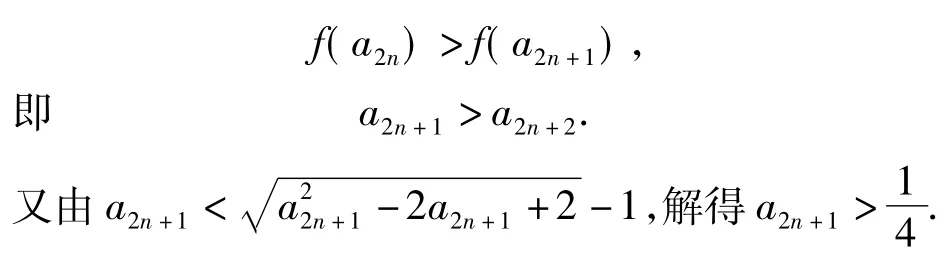
点评数列是一种特殊的函数,动态的函数观点是解决数列问题的有效方法.数列中的恒成立问题常常转化为函数的最值问题来解决.用函数的思想方法去研究数列问题不仅能加深对数列的理解,也有助于学生解题思维能力的培养及增强应用函数思想解题的意识.
4 精题集萃
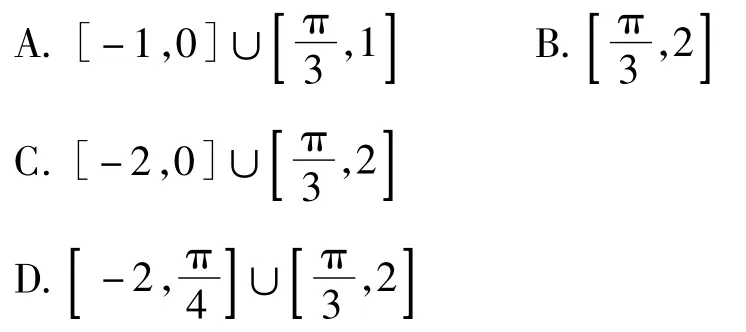
2.在△ABC中,若sin(A-B)=1+2cos(B+ C)sin(A+C),则△ABC的形状一定是()
A.等边三角形 B.不含60°的等腰三角形
C.钝角三角形 D.直角三角形
3.如图3,棱长为1的正方体ABCD-A1B1C1D1,点M在与正方体的各棱都相切的球面上运动,点N在△ACB1的外接圆上运动,则线段MN长度的最小值是()
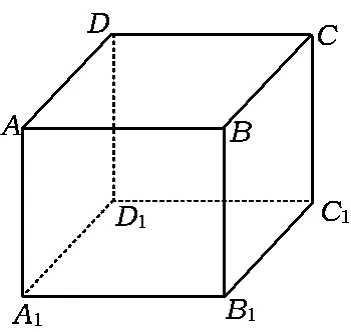
图3
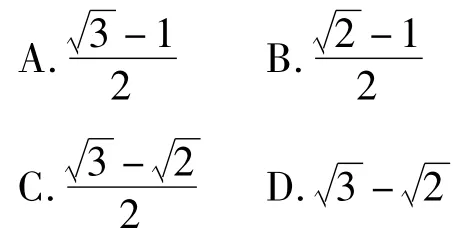
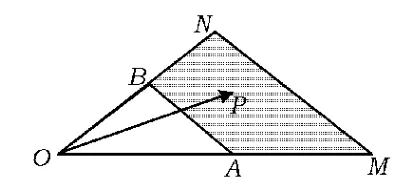
图4
5.若实数a,b,c满足2a+2b=2a+b,2a+2b+ 2c=2a+b+c,则c 的最大值是______.
7.已知A(cosα,sinα),B(cosβ,sinβ),其中α, β为锐角,且
1)求cos(α-β)的值;
8.已知数列{an}满足a1=a,an+1=Sn+ (-1)n,n∈N*,且是等比数列.
1)求a的值;
2)求出通项公式an;
9.如图5,设椭圆C1:(其中a>b> 0)的左、右焦点分别是F1,F2,下顶点为A,线段OA的中点为B(其中O为坐标原点).若抛物线C2: y=x2-1与y轴的交点为B,且经过点F1,F2.
1)求椭圆C1的方程;
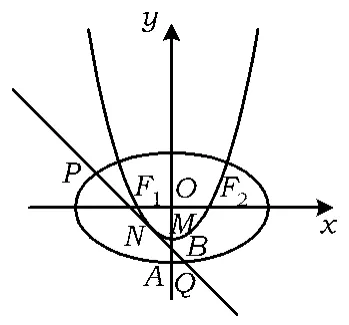
图5
参考答案