构造多项式解答竞赛题
2015-12-08卢学谦泰安市第一中学山东泰安271000卢健莱城区羊里中学山东莱芜271118
●卢学谦(泰安市第一中学山东泰安271000)●卢健(莱城区羊里中学山东莱芜271118)
构造多项式解答竞赛题
●卢学谦(泰安市第一中学山东泰安271000)●卢健(莱城区羊里中学山东莱芜271118)
多项式理论是代数学的重要内容.恰当地根据题目的特点构造多项式,然后用一些简单的多项式理论解答竞赛题,往往能起到非常重要的作用.例如,2011年全国高中数学联赛二试中的第2题就构造了一个简单的多项式,其解答令人叫绝,叹为观止.本文通过一些实例进行探究,供读者参考.
1 在组合题中的应用
例1设a1,a2,…,a2011;b1,b2,…,b2011为互不相等的实数,将它们按如下方法填入一张2 011×2 011的方格表中,即在位于第i行与第j列的交叉处的方格中填入数ai+bj.已知表中任一行各数的乘积皆是2 011,证明:表中任一列各数的乘积也是2 011.
证明第i行的各数乘积为(ai+b1)(ai+b2)…(ai+b2011)=2 011(其中i=1,2,…,2 011),从而a1,a2,…,a2011是多项式

的2 011个相异根,因此该多项式又可表示为

取x=-bk(其中k=1,2,…,2 011),则由式(1)得
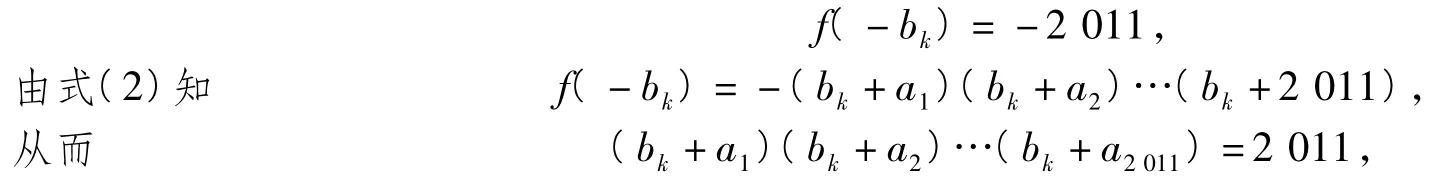
左边恰是表中第k列各数之积,k=1,2,…,2 011.
(1994年中国数学奥林匹克竞赛试题)
证明构造多项式函数f(x)=(1+x)2n+1.一方面,需证等式右边显然是f(x)的n次项系数.另一方面,
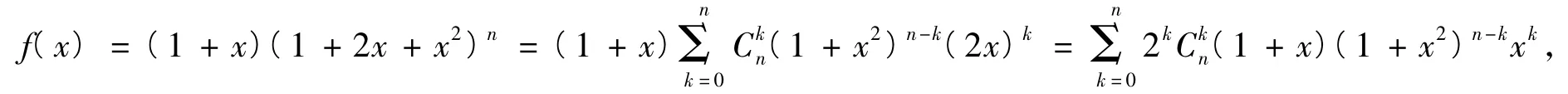
当n-k为偶数时,(1+x)(1+x2)n-k中xn-k的系数为;当n-k为奇数时,(1+x)(1+x2)n-k中xn-k的系数为,从而对k=0,1,…,n,在中xn的系数总是,故f(x)的n次项系数为.
例3证明:对任意正整数n,二项式系数Cmn(其中0≤m≤n)中,奇数的个数是2的幂.
证明将n用二进制表示为n=2α1+2α2+…+2αk(其中α1≥α2≥…≥αk),从而
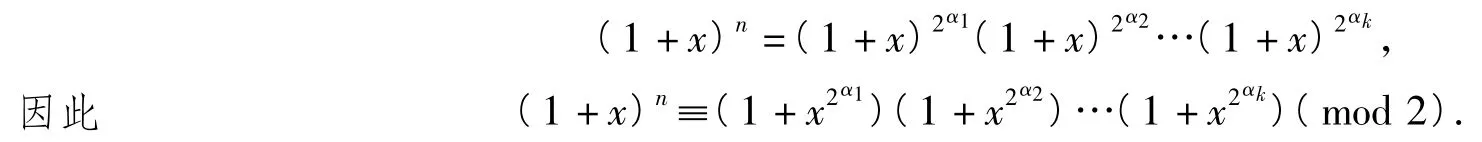
右边的多项式恰含2k个项,它们的系数为1(奇数).即(1+x)n的展开式中,恰有2k项系数,为奇数.
2 在数论题中的应用
证明注意到m=2·3·4·…2 010+1·3·4·…·2 010+…+1·2·3·4·…·2 009为集合M={1,2,…,2 010}中每次取2 009个元素的乘积之和,故可考虑以1,2,…,2 010为根的多项式
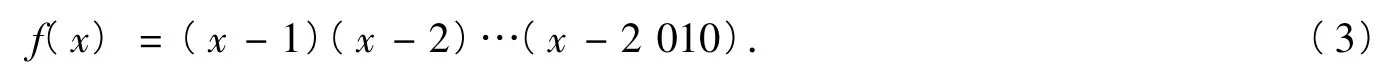
将其展开后,设

其中g(x)=(a1x2008+a2x2007+…+a2009)x.因为2 011为质数,所以当x∈M时,2 011|(x2010-1)(据费尔马小定理).又因为2 011|(2 010!+1)(据威尔逊定理),且当x=1,2,…,2 010时,f(x)=0,所以当x=1,2,…,2 010时,皆有2 011|g(x),因此g(x)的所有系数皆是p=2 011的倍数.令ai=pbi,i=1,2,…,2 009,有

(其中p=2 011).由式(3)知,f(2 011)=2 010!;在式(4)中取x=2 011有

由式(5),得2 0112|a2009;由式(3)知a2009就是f(x)展开式中的一次项系数,即为m,因此可得2 0112|m (注意:本题中的2 011可改为任意奇质数p).
例5对于集合A={a1,a2,…,am},记P(A)=a1a2…am.设A1,A2,…,An(其中)是集合{1, 2,…,2 010}的所有99元子集,求证:2 011|.
证明构造多项式f(n)=(n-1)(n-2)…(n-2 010)-n2010-2 010!(其中n∈N+).注意2 011为素数,由威尔逊定理知2 010!≡-1(mod 2 011),又由费尔马定理知当2 011=n时,n2010≡1(mod 2 011),因此对于每个n∈N+,
1)当2 011=n时,f(n)≡(n-1)(n-2)…(n-2 010)≡0(mod 2 011);
2)当2 011|n时,f(n)≡(n-1)(n-2)…(n-2 010)-2 010!≡2 010!-2 010!≡0(mod 2 011),即f(n)≡0(mod 2 011)在mod 2 011意义下有2 011个解,而f(n)是一个2 009次多项式,对于每个n∈N+都有2 011|f(n),故f(n)的各项系数都能被2 011整除.
3 在代数题中的应用
例62 011个实数x1,x2,……,x2011满足方程组,n=1,2,…,2 011.试计算的值.
解构造2 011次多项式

根据条件,当x分别取1,2,…,2 011时,皆有f(x)=0,因此有常数c,使
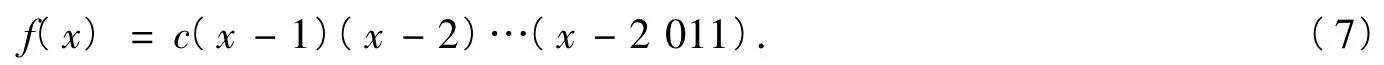


解当n=1时,显然解为x1=1.以下不妨设n≥2,此时构造多项式函数

而另一方面,结合原方程组可得

对照可得f(1)=0,这说明x1,x2,…,xn中有一个为1,不妨设xn=1,则剩下的未知数x1,x2,…,xn-1满足方程组(其中k=1,2,…,n).以此类推,可得所有的xi=1(其中k=1,2,…,n),从而原方程组的解为x1=x2=…=xn=1.
[1]厉军萍.巧用构造法证明不等式竞赛题[J].中学教研(数学),2012(6):32-36.
[2]何豪明.解一道竞赛题的“通性通法”[J].中学教研(数学),2014(12):44-45.
