嫦娥三号软着陆控制研究

宋立甲，李威，马文联

（长春理工大学 理学院，长春 130022）

嫦娥探月工程开始于2007年，探月卫星嫦娥一号于2007年发射，采用了调相技术和轨道修正技术，对月球的地貌进行探测。嫦娥二号于2010年10月成功发射，设计直接的地月轨道，实现了升、降轨控制，获得了全月球图卫星。

嫦娥三号于2013年12月2日发射，14日晚成功着陆在月球的虹湾以东区( )19.51°W,44.12°N 。CE-3的安全着陆为此后的月面巡视勘察、月面生存、深空测控通信与遥操作任务打下基础。CE-3的软着陆分为以下六个阶段：（1）着陆准备阶段，着陆准备轨道为椭圆轨道，近月点高15km，远月点高100km，CE-3在近月点处减速，进入主减速阶段；（2）主减速阶段，借助大推力减速发动机，在15km到3km的高空减速，实现大致落在目标上方，速度近似为57m/s的目标；（3）快速调整阶段，调整探测器姿态，使主发动机的推力方向竖直向下；（4）粗避障阶段，在2.4km到100m的空中，通过拍摄的高程图，避开比较大的陨石坑、山丘等障碍物；（5）精避障阶段，在100m到30m的低空拍摄照片，获取高精度高程图，避开较小的陨石坑、山丘；（6）缓速下降阶段，经过精避障阶段探测器已位于目标上方，本阶段的任务是借助推力发动机，使推力发动机在距月面4m的高度悬停。

嫦娥三号成功发射前后，许多人探索嫦娥三号的轨迹和控制。蒋瑞等人［1］对水平和竖直方向都利用非线性变结构控制方案，控制角速度和角加速度，通过对相应的哈密尔顿函数采用极小值原理来得到变结构控制，完成轨道设计与控制；张洪华等人［2］详细给出了嫦娥三号自主给出避障程序设计要求、流程，基于自主避障选取算法及制导过程；贾阳等人［3］利用嫦娥三号探测器获得的高程图与嫦娥二号获取的着陆区高分辨率DOM影像进行联合处理，使用SIFT特征匹配、图像单应变换和立体视觉测量等技术，进行精确的定位；单永正等人［4］用约束变换技术将不等式约束近似处理，分段的常数逼近最优解，增加参量部不断逼近求解；王鹏基等人［5］假定推力方向始终与速度方向相反，建立二维力学模型，在假定下降高度与飞行距离成线性关系的前提下，通过微分变量代换等方法给出月面角等参数的解析解，其缺点在于没有考虑燃耗而直接以假设的形式给出制导率；叶培建等人［6］阐述了探测器的各个阶段的主要处理方法，着陆缓冲技术采用了“悬臂式”的构型设计、压紧释放与展开锁定装置与辅助缓冲器的集成设计等创新设计方案，自主导航与遥操作控制采用立体视觉技术实现月面未知环境的三维恢复与重建，提出了多种适应月面地形特征的启发式路径搜索算法，完成路径规划；杨维廉等人［7］在考虑燃耗、光照、月球重力场异常等因素的情况下给出CE-1使命轨道、地月转移轨道、调相轨道的类型和基本参数，并且预算了CE-1在各个阶段所需的燃料，但是文章只是综述了结果，并未给出CE-1轨道、燃耗的求解方法，并且没有分析避障阶段的路径、燃耗。

嫦娥三号应用微波测距测速敏感器、激光测距敏感器和激光三维成像敏感器等一系列新型敏感器对软着陆中导航和制导以及避障控制策略设计，并研制出高精度的变推力发动机，精度为6.25N，实现了推力从1500N到7500N连续变化。嫦娥三号的成功发射在技术上和理论上有较大的突破性，本文从理论上考虑了推力变化、探测器受力、着陆点的平整度、燃料消耗等因素，简化多维控制方程，研究嫦娥三号的运行轨迹的控制策略。

1 嫦娥三号轨迹研究

经过万有引力公式

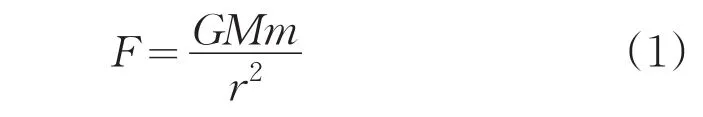
计算出CE-3与地球的相互作用力远小于月球与CE-3的作用力，因此不考虑CE-3与地球之间的相互作用，把问题转为两体问题。同时，由于月球自转带来的向心力和科里奥利力远小于月球的引力，因此本文不考虑自转。

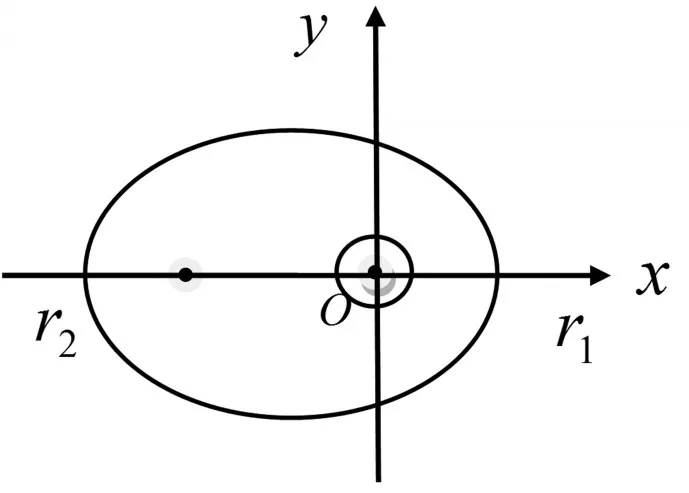
图1 月心坐标系下的着陆准备轨道

建立月心坐标系，如图1所示。图中，O点表示月球，以月球、近月点、远月点所在的平面建立坐标系，x、y分别表示近月点与远月点的所在椭圆的长轴与短轴方向。

确定近月点、远月点的位置，可以明确嫦娥三号的运行轨迹所在的平面.假设近月点与远月点的速率为v1、v2，到月心的距离为r1、r2。

由角动量守恒和机械能守恒可以得到

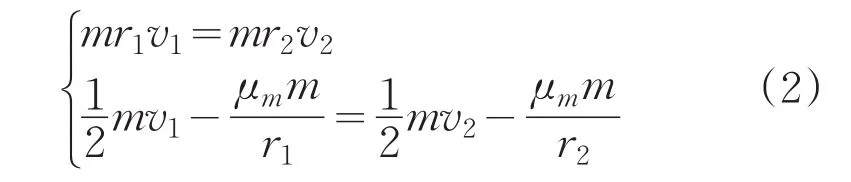
其中，μm为高斯常数，μm=GM，根据上式可以求出近月点、远月点的速度为 v1=1.692km/s，v1=1.614km/s。嫦娥三号的水平速度由1.692km/s减小到0，共经历了450s，假设此过程中推力发动机是恒力做功，又嫦娥三号受到的月球的重力也可以看做是恒定的，故其在水平方向上的加速度也是恒定的。

由式（3）：

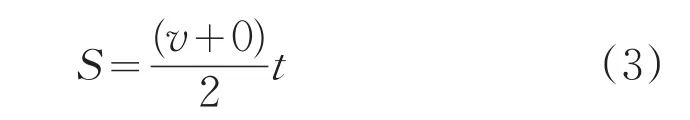
得嫦娥三号的水平移动的距离为S=380.7km。根据椭圆第一定义，

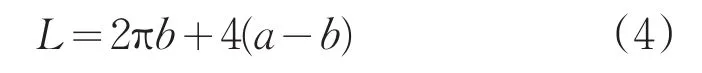
其中，a、b分别是椭圆的长、短半轴长，L为周长。可求得月球经线周长为10913.823km，而

代入数值得θ=12.558°。近月点为（19.51°W,31.562°N），海拔为 15km，远月点为（160.49°W,31.562°N）海拔为100km。

2 主减速阶段

本阶段通过控制反推力的大小和方向，使减速过程在满足始态条件和终态条件的前提下，使得燃耗最小。可以证明当反推力的大小为最大值时燃耗最小，因此根据比冲的定义可以得出：

所以

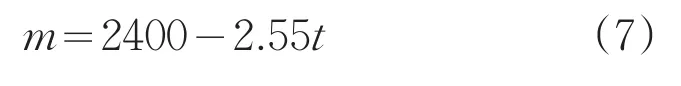
单位为kg。

在主减速过程中，探测器受月球的引力和减速器的推力，探测器受力情况如图2所示。

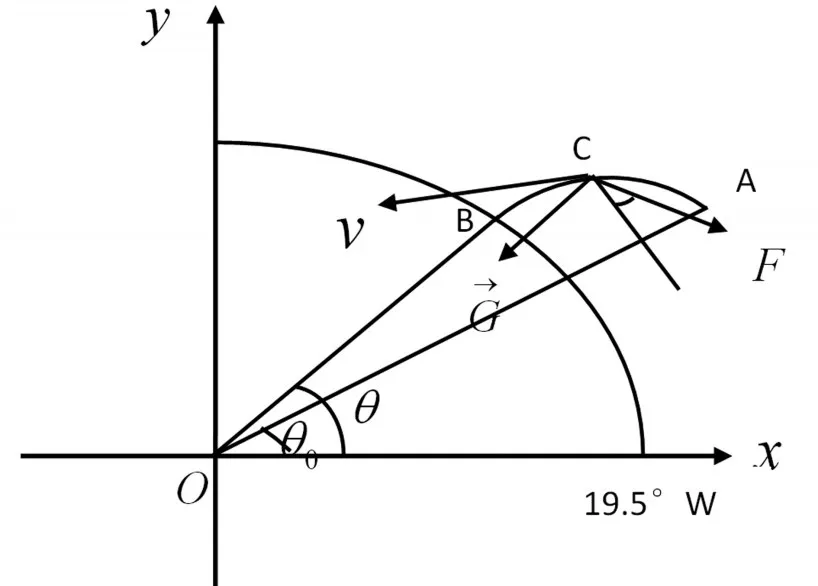
图2 月心坐标系下CE-3在主减速阶段的受力图

图中，上述平面为球心与目标着陆点所构成的平面，O点表示月球球心，x、y分别表示水平与竖直的半径方向；根据牛顿第二定律，建立以下力学模型：

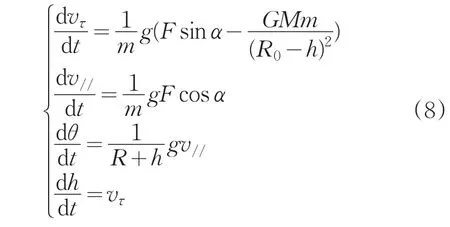
其中，vτ是径向的速度，v//是法向的速度，θ是纬度，F是反推力的大小，α是反推力与切向的夹角。

在主减速阶段，探测器从15km下降到3km，从31.5°N飞到44.1°N，即 h 的变化范围是［3，15］单位是km，Δθ为12.6°，基于此得出如下近似结果：月球的引力的大小在主减速阶段为常量，探测器在A点和B点的受力之比为：

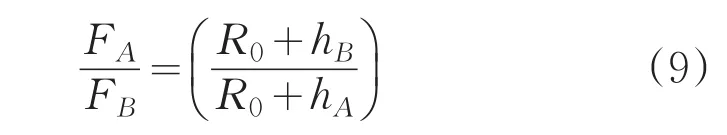
代入数值计算得出探测器在A点和B点的受力之比为0.99，所以可以认为主减速阶段引力的大小不变，不妨令整个过程中月球的引力均为mgm。探测器绕月心飞过的角度可以视为小角度。

根据以上两个近似结果，对图2和（2）式进行简化，探测器在主减速阶段的受力如图3所示。

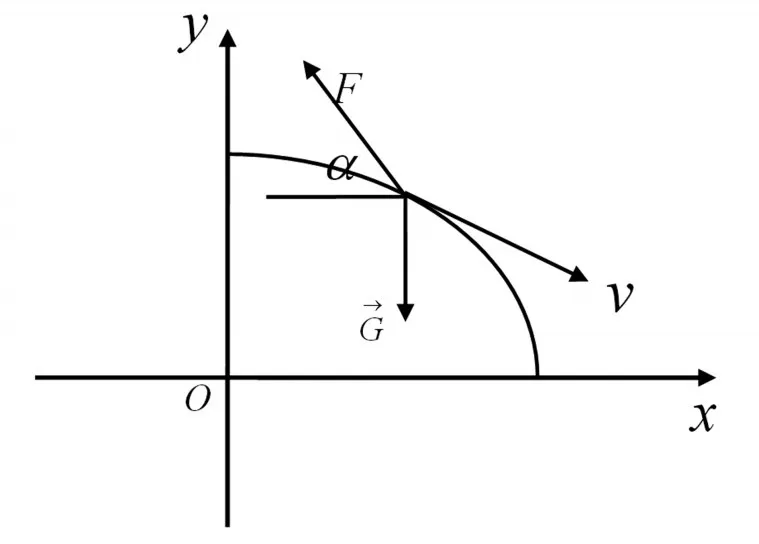
图3 月球表面坐标系下CE-3在主减速阶段的受力图

图中，上述平面为球心与目标着陆点所构成的平面，O点表示月球球心，x、y分别表示水平与竖直的半径方向；探测器的状态函数为：

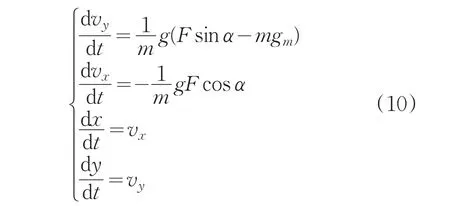
初态条件为：

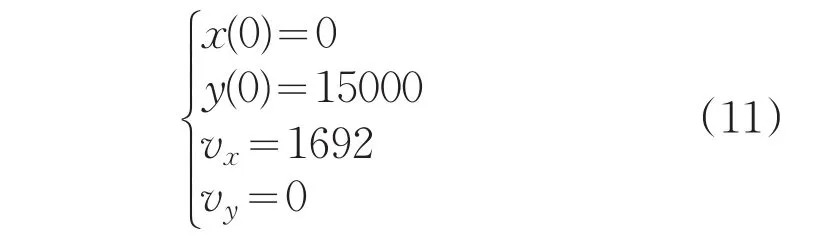
末态条件为：

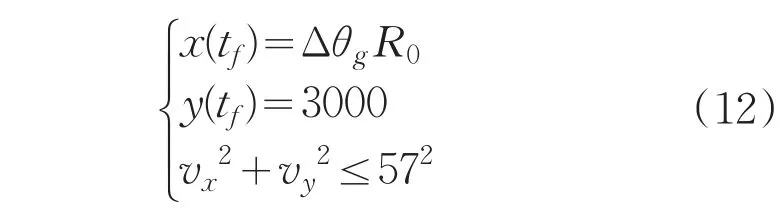
目标函数为：

反推力与x轴反方向的夹角α为时间t的连续函数，不妨设其4阶泰勒展开式为α(t)=A⋅t4+B⋅t3+C⋅t2+D⋅t+E，所以问题转化为选取合适的参数A,B,C,D,E和tf，使得式（13）取最大值，同时满足约束条件是（11）和式（12）。本问题直接采用MATLAB优化工具箱进行寻优。最终求解出，单位为m/s，m=1252.5kg。快速调整阶段始末状态如表1所示。

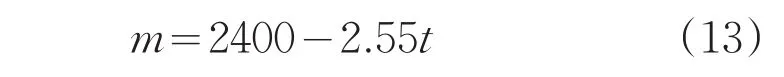
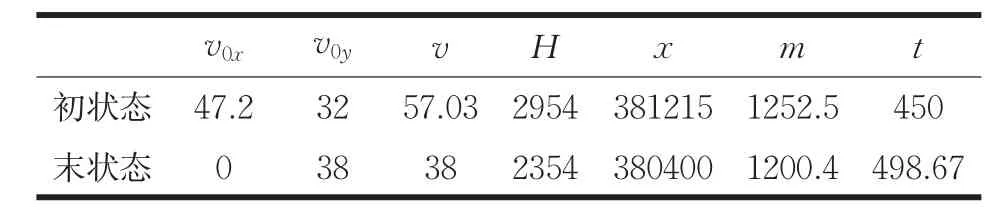
表1 CE-3快速调整阶段始末状态

表中所有物理量的单位为国际标准单位。

3 避障阶段

粗避障阶段分析星下光学敏感成像，调整姿态，避开较大陨石坑。降落至100米时，分析高分辨率的三维成像，精细避开障碍物，完成避障任务并确定着陆位置。根据收集的资料，嫦娥三号降落应满足安全着陆的条件：

（1）为保证光学成像敏感器视场对准预着陆区，着陆器采用用45∘接近直线下降方式逐步接近着陆区；

（2）通过光学成像器检测大的障碍，确定安全着陆区并避障，最终到达着陆区上方100m，相对月面的速度接近0，航向距离为3km；

（3）在距月面100m的精避障，有变推力发动机抵消着陆器重力，水平速度为0，轨迹为斜向下降到着陆点；

（4）针对着陆器的着陆点要求，着陆点月面倾角小于8°，凹坑和凸起（20cm）不同时出现（垂直最大速度3.8m/s，水平速度为1m/s，最大姿态角为正负4°）条件下，可以安全着陆。

以满足上述条件的情况为安全着陆的前提，下面考虑消耗燃料最少的着陆位置，则避障阶段搜寻最优位置的两个指标是着陆面的平整度和燃料消耗。

对返回的数字高程图进行平整度分析：

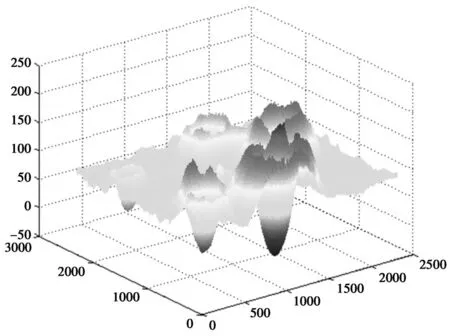
图4 2400m处月表成像

图4是对预着陆区域2400米处数字高程图的处理后得到等高图，可以直观粗略的看出各个位置的凹凸情况，图5是量化后的月表粗糙程度，将预着陆区域划分为5×5小区域，每一块内有460*460个点，令凹凸处的点为0，平坦处的点为1，逐点显示在各分块中，并将各点的粗糙度相加，和越大说明该区域越平坦，可以看出最为平缓的是区域（3，3）。此时嫦娥三号在月面的垂直投影位于预定着陆区域的中心位置，且中心位置（3，3）的值为210094最为平缓。

图5 2400m处月表粗糙度图

对于燃料消耗最少的分析如下，根据上述给出的燃料消耗最小的目标函数（13）式以得到图6中圆形区域：

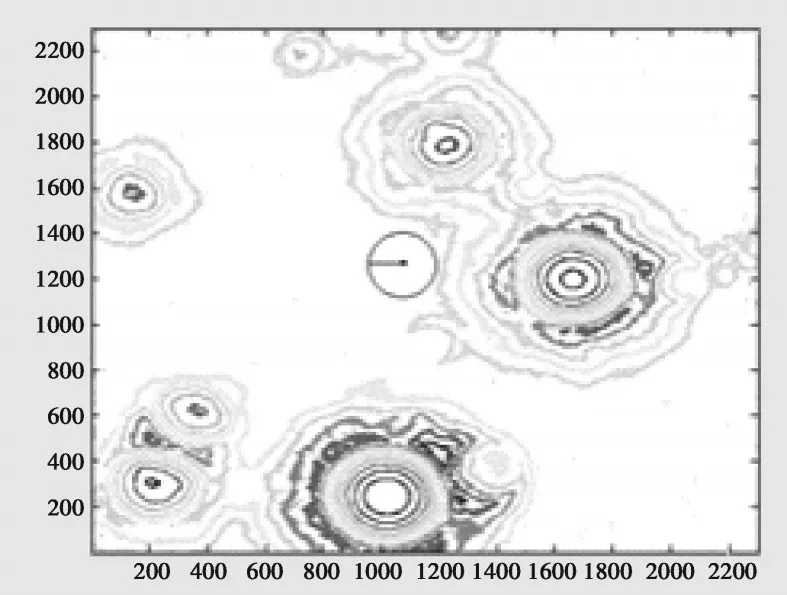
图6 1200m处燃耗较小的目标区域

精障碍检测主要识别粗糙度和燃料消耗，根据这两项综合确定安全着陆点。两项指标有相当的权重，令均为0.5，则应该选择的位置为（3，3）。当到达100m时，进行精避障阶段，实现角度的调整，方法类似粗避障阶段，处理后可以得到图7、图8。

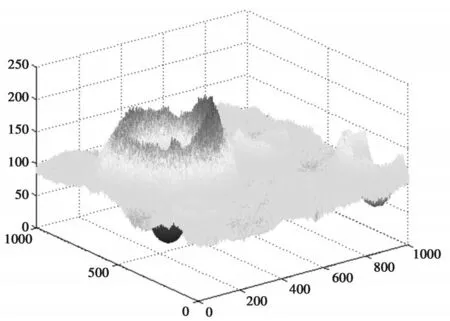
图7 100m处月表成像

图8 100m处月表粗糙度图

对于燃料消耗最少的分析，根据上述给出的燃料消耗最小的目标函数可以得到图9中圆形区域。

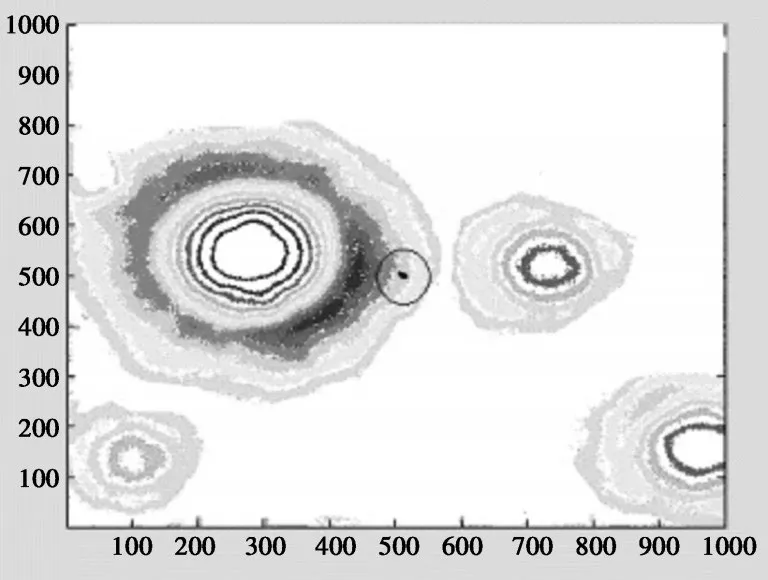
图9 100m处燃耗较小的目标区域

综合考虑两个因素后，根据图8、图9，本文选择的着陆点为（5，5）中心位置降落。

4 结论

本文根据嫦娥三号环月的近月点远月点位置以及运行轨迹问题进行探讨。在目标速度、目标位置的约束下，考虑燃耗最小、运行安全等因素，实现六个阶段的轨道设计，通过控制每一个阶段变推力的大小、方向等物理量实现对嫦娥三号的控制，同时，给出CE-3在各个阶段的燃耗、速度、位置等状态。

本文将嫦娥三号的无穷维求解参量转化为二维计算，未能全面地考虑整个轨迹过程中影响因素，同时缺少对光照、月球重力场异常等因素的考虑。在未来的研究当中，应当参考以往各个国家对月球的探测成果，将着陆点的物质丰富性、光照、电磁场等同样具有实际意义的因素考虑在内，并给予各个因素以权重，综合设计落月的轨道与位置。

［1］蒋瑞，韩兵.嫦娥三号着陆控制研究与软件仿真［J］.微型电脑应用，2012，28（2）：17-34.

［2］张洪华，梁俊，黄翔宇，等.嫦娥三号自主避障软着陆控制技术［J］.中国科学，2014，44（6）：559-568.

［3］贾阳，刘少创.利用降落影像序列实现嫦娥三号系统着陆 点 高 精 度 定 位［J］.中 国 科 学 ，2014，59（19）：1838-1843.

［4］单永正，段广仁，张烽.月球精确定点软着陆轨道设计及初始点选取［J］.宇航学报，2009，30（6）：2100-2103.

［5］王鹏基，张熇，曲广吉.月球软着陆重力转弯轨道设计与分析［J］.中国宇航学会深空探测技术专业委员会第二届学术会议论文集，2005：329-331.

［6］叶培建，黄江川，孙泽洲，等.中国月球探测器发展历程和经验初探［J］.中国科学，2014，44（6）：543-558.

［7］杨维廉，周文艳.嫦娥一号月球探测卫星轨道设计［J］.航天器工程，2007，16（6）：16-24.