例谈三角函数与平面向量的复习
2015-12-07林光来灵溪第二高级中学浙江苍南325800
●林光来(灵溪第二高级中学浙江苍南325800)
例谈三角函数与平面向量的复习
●林光来(灵溪第二高级中学浙江苍南325800)
1 命题分析
纵观近几年的浙江省数学高考试题,出现了一些富有时代气息的三角函数与平面向量考题,它们形式独特、背景鲜明、结构新颖,主要考查考生分析问题、解决问题的能力和处理交汇性问题的能力.浙江省数学高考试卷中一般有3~5个三角函数与平面向量的题目,分值约占全卷的10%~20%.三角函数的图像与性质的考查,以图像的变换,三角函数的单调性、奇偶性、周期性、对称性、最值等作为热点内容,并且往往与三角变换公式相互联系,有时也与平面向量、解三角形或不等式内容相互交汇.三角恒等变换中公式比较多,包括两角和与差的正弦、余弦和正切公式、二倍角公式等等,合理运用三角公式是解决三角函数的图像与性质、三角恒等变换等问题的关键.在高考题中,突出考查三角公式所涉及的基本运算,重点考查三角函数名称、角、关系式的变换,经常会结合三角形、平面向量等知识进行综合考查.而解三角形是三角函数的一个应用,《考试说明》中明确提出:“必须掌握正弦定理、余弦定理,并能运用这2个定理解决实际问题”.浙江省数学高考试题对正、余弦定理的考查一般集中在求解三角形的边、角、面积及判断三角形形状等方面.
平面向量从命题角度上看,主要围绕平面向量运算设计试题,着重考查平面向量的概念、线性运算、坐标运算和数量积运算,其中,对平面向量的数量积运算的考查尤为突出.近几年的浙江省数学高考试题,特别强调几何背景和代数性质的结合,命题热点主要集中在以下3个方面:1)利用平面向量的几何意义来解决问题;2)利用基向量转化来解决问题;3)利用坐标法来解决有关问题.平面向量是代数、平面几何、三角函数、解析几何等知识的网络交织点,因此数学高考卷也会在平面向量与三角函数的交汇处设计试题.
2 典题剖析
2)求函数f(x)的最小正周期及单调递增区间.
(2014年福建省数学高考理科试题第16题)

2)由正弦与余弦的二倍角公式,以及三角函数的化一公式,将函数f(x)化简为

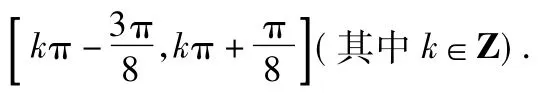
评注该题属于中等偏易题,主要考查了三角函数的性质、正弦与余弦的二倍角公式及三角函数的化一公式等基础知识,同时考查了运算求解能力.解决三角函数问题要重视三角函数的“三变”:变角、变名、变式.变角即对角的分拆要尽可能化成同名、同角、特殊角;变名即尽可能减少函数名称;变式即对式子变形要尽可能有理化、整式化、降低次数等.在解决求值、化简、证明问题时,一般是观察角度、函数名、所求问题的整体形式中的差异,再选择适当的三角公式进行变形.
例2已知向量a=(m,cos2x),b=(sin2x,n),设函数f(x)=a·b,且y=f(x)的图像过点和点
1)求m,n的值.
2)将y=f(x)的图像向左平移φ(其中0<φ<π)个单位后得到函数y=g(x)的图像.若y=g(x)的图像上各最高点到点(0,3)距离的最小值为1,求y=g(x)的单调递增区间.
(2014年山东省数学高考理科试题第16题)
分析1)由题意知
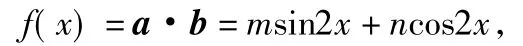
2)由第1)小题知
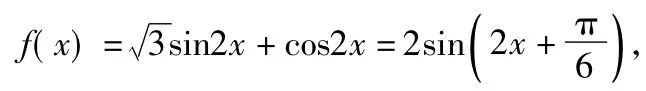
由题意知
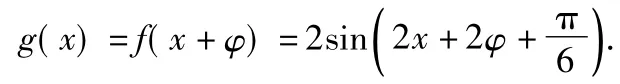
将(0,2)代入y=g(x),得

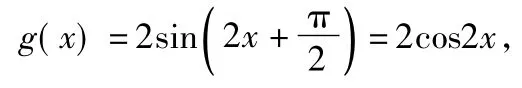
评注该题考查了平面向量的数量积、三角函数的化简、三角函数的图像与性质等基础知识,同时考查了运算求
解能力、推理论证能力.三角函数公式非常多,使用方式灵活多样,在三角函数复习中不仅要让学生学会正用、逆用、变形使用公式,还要让学生掌握公式及其变形的特点,提高分析问题、解决问题的能力,从而灵活使用公式,正确地进行求解.
例3在△ABC中,a,b,c分别为角A,B,C所对的边,acosB=bsinA,且a2-b2=bc,试判断△ABC的形状(改编题).
分析1要判断三角形形状可以从边的角度进行解决:由acosB=bsinA及正弦定理可得;由a2-b2=bc及余弦定理可得,代入a2-b2=bc并化简整理得b=c.因此,故△ABC为等腰直角三角形.
分析2判断三角形形状也可以从角的角度来考虑:利用正弦定理、余弦定理可得
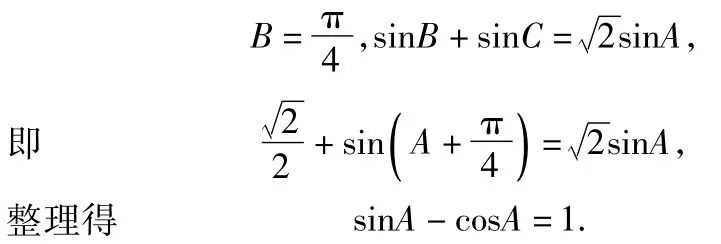

故△ABC为等腰直角三角形.
评注本题主要考查了正弦定理、余弦定理等基础知识,同时也考查了运算求解能力.在平时复习中要让学生在解决问题的过程中熟悉利用正、余弦定理进行“角边互化”,对所给的边角关系式一般要先化为只含边之间的关系或只含角之间的关系,再进行判断.
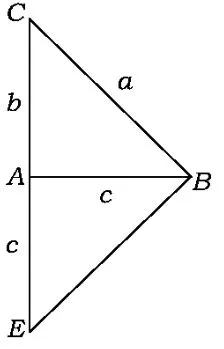
图1
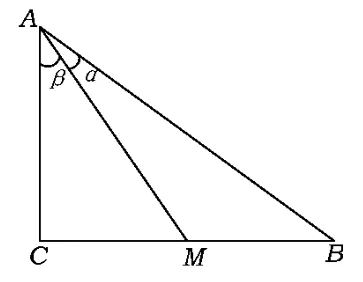
图2
(2013年浙江省数学高考理科试题第16题)
分析1(利用三角公式)如图2,设BC=a,AC=1,AB=c,令∠BAM=α,∠MAC=β.利用两角和的正切公式可以解得,从而

分析2(利用正弦定理)令AB=c,AC=b,BC=a.在△ABM中,,即
分析3(坐标法)建立如图3所示的直角坐标系,令M(1,0),B(2,0),A(0,b),则∠AMC=∠B+∠BAM.利用两角和的正切公式解得,从而
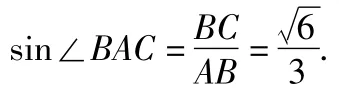
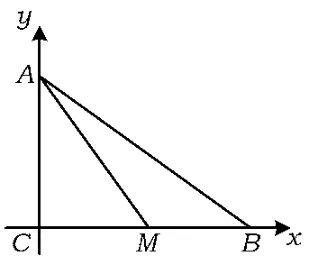
图3
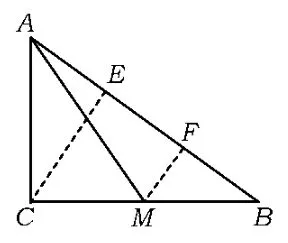
图4
分析4(平面几何法)如图4,经过点C,M作AB的垂线.设MF=1,可得CE=2.由于,故AM=3,在Rt△ABC中,CE⊥AB,从而
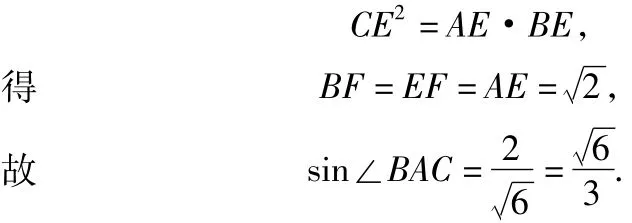
评注此题主要考查了解三角形的知识,同时考查了学生的运算能力、推理论证能力和数形结合的思想,考查学生综合运用数学知识和思想方法解决问题的能力.在平时的复习中要对一些题目从不同的角度、利用不同的思想方法来解决,有效地提升学生思维的灵活性、多样性和层次性.
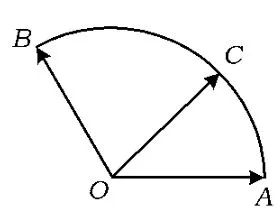
图5

图6
(2009年安徽省数学高考理科试题第14题)
分析1(利用正弦定理)如图6,设∠AOC=α(其中α∈[0°,120°]),过点C作CD∥OB交x轴于点D,可得x=|OD|,y=|DC|,∠ODC=60°,∠C=120°-α,由正弦定理可得
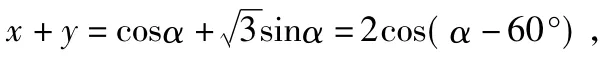
再利用α的范围求得x+y的最大值为2.
分析2(坐标法)建立如图6所示的直角坐标系,易知A(1,0),,C(cosα,sinα).由,得
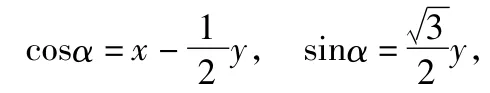
分析3由题意知
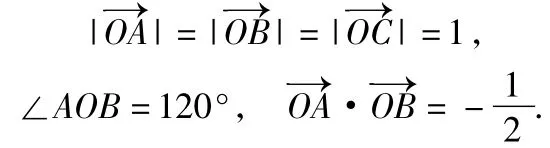
设∠AOC=α(其中α∈[0°,120°]),则


再利用基本不等式求得x+y的最大值为2.
评注该题是一道以圆为载体、以向量为背景的最值问题,问题设计多角度、多视角、多层次地考查了学生的数学思维能力,同时考查了学生对数学本质的理解能力和数学素养.该题素材朴实,形式平淡,而求解过程精彩纷呈、妙趣横生.解决该题可以从不同的角度出发,内容涉及代数、平面几何、三角函数、解析几何等知识,蕴藏着数学方法.在平时复习中应注重利用这样的问题来提升学生的数学思维能力.
例6设△ABC,P0是边AB上一定点,满足,且对于边AB上任一点P,恒有,则( )
A.∠ABC=90° B.∠BAC=90°
C.AB=AC D.AC=BC
(2013年浙江省数学高考理科试题第7题)
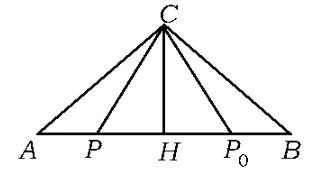
图7
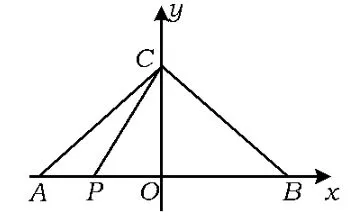
图8

恒成立,整理后得

恒成立,只需Δ=(t+1)2-4t≤0即可,从而t=1,即AC=BC.
分析2(坐标法)如图8,建立直角坐标系.设A(a,0),B(b,0),C(0,c),P(x,0),则
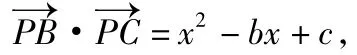
分析3(利用极化恒等式)取BC的中点O,则
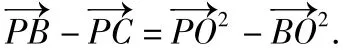
评注该题主要考查了平面向量的数量积运算、不等式恒成立等知识,同时考查了学生的运算能力、转化与化归能力、数形结合思想.本题的解决方法还有很多,除了上面给出的3种方法外,还可以利用基本不等式、基向量进行转化、向量回路法等等.需要考生熟练掌握向量数量积运算的方法,这正是解决问题的关键.而数量积的运算一般有3种视角:一是直接利用数量积的定义;二是利用坐标法转化为代数运算;三是利用基底进行转化.
3 精题集萃
A.4 B.3 C.2 D.1
3.已知a,b是单位向量,a·b=0.若向量c满足|ca-b|=1,则|c|的取值范围是( )
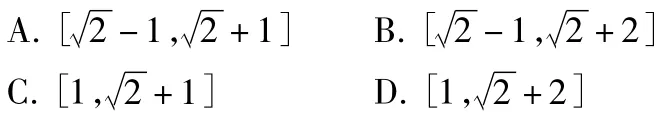
5.在△ABC中,角A,B,C所对的边分别为a,b,c,满足b2+c2-a2=bc,,,则b+c的取值范围是______.
6.已知四边形ABCD是矩形,AB=2,AD=3,E是线段BC上的动点,F是CD的中点.若∠AEF为钝角,则线段BE长度的取值范围是______.
7.如图9所示,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,则的最大值是______.
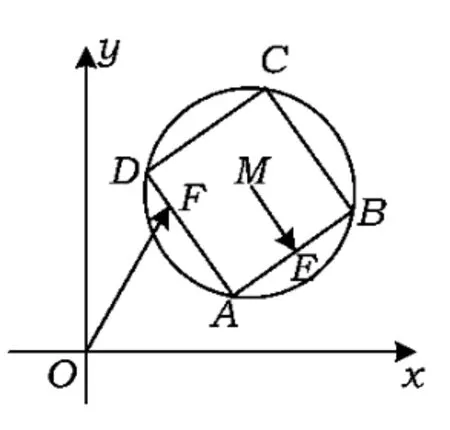
图9
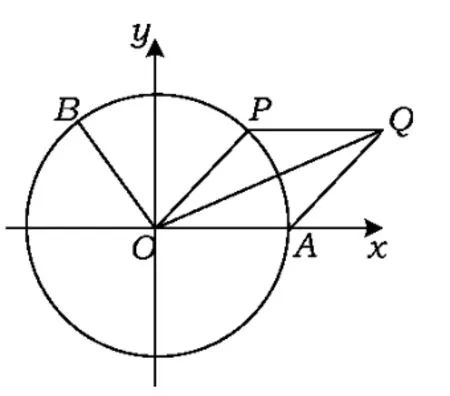
图10
1)求f(x)的单调递增区间;
2)在△ABC中,3个内角A,B,C的对边分别为a,b,c,已知,2a=b+c,bc=18,求a的值.
9.在△ABC中,角A,B,C所对的边长分别为a,b,c,且acosC,bcosB,ccosA成等差数列.
1)若a+c=4,求AC边上中线长的最小值.
10.如图10所示,A是单位圆与x轴正半轴的交点,点B,P在单位圆上,且,∠AOB=α,∠AOP=θ (其中0<θ<π),,四边形OAQP的面积为S.
(1)求cosα+sinα;
参考答案


