集合与函数复习要点探析
2015-12-07沈新权嘉兴市第一中学浙江嘉兴314050杨月荣嘉善高级中学浙江嘉善314100
●沈新权(嘉兴市第一中学浙江嘉兴314050)●杨月荣(嘉善高级中学浙江嘉善314100)
集合与函数复习要点探析
●沈新权(嘉兴市第一中学浙江嘉兴314050)●杨月荣(嘉善高级中学浙江嘉善314100)
集合与函数是高中数学的重要内容之一,从历年浙江省的数学高考来看,对集合与函数的考查相对稳定,既有小巧灵活的容易题,也有新颖别致的中等题,更有内涵丰富的压轴题,其中不少问题的解决对考生有较高的能力要求.
1 知识内容
根据2012版的《浙江省普通高中学科教学指导意见》,集合与函数的主要考查内容有:
1)理解集合语言的含义,会进行简单的集合运算;
2)了解4种命题的含义及其相互关系,理解必要条件、充分条件与充要条件的含义;
3)理解函数的概念,会求一些简单的函数定义域和值域;
4)理解函数的奇偶性和单调性,会判断函数的奇偶性,会讨论和证明函数的单调性;
5)理解指数函数、对数函数和幂函数的概念、图像和性质,并学会运用函数图像理解、研究函数的性质;
6)了解函数零点的概念,理解并掌握连续函数在某个区间上存在零点的判定方法;
7)认识不同函数模型的增长差异,并了解函数模型在解决实际问题中的作用;
8)关注思想方法的渗透,如数形结合、分类讨论、化归等思想方法.
2 命题分析
从历年的高考试题来看,集合与函数作为高中数学的基础知识,在数学的其他分支中有着极其广泛的应用,因此集合与函数一直是高考中的主干题型和热点内容.集合内容在高考中主要以选择题或填空题的形式出现,命题重点呈现3个方面:1)以函数的定义域、值域、不等式的解集为背景考查集合之间的交集、并集及补集的基本运算和集合之间的包含关系;2)以新定义集合以及集合运算为背景考查元素与集合之间的关系;3)集合与其他知识相交汇,常与函数、方程、不等式、平面向量、三角等知识相结合.常用逻辑用语的考查形式多以选择题为主,命题重点主要有:命题的4种形式及其相互关系,主要考查命题的4种形式及命题的真假判断;含有简单逻辑联结词的命题真假的判断以及对充分必要条件的考查,主要考查充分必要条件与集合、函数、方程、数列、三角函数、不等式、平面向量、立体几何中的线面位置关系相交汇的问题.对于函数性质及基本初等函数的考查,在2015年的浙江省数学高考试卷中,试题形式将在选择题、填空题以及解答题中都会有所体现,其命题的重点主要有2个方面:1)考查函数的概念、图像、性质或者是几个方面的综合;2)考查交汇性问题,主要是幂函数、指数函数、对数函数知识块间的交汇,或与抽象函数、复合函数、函数零点、数列、不等式、三角等知识交汇来考查.
高考中对集合与函数这些内容的考查有涉及的知识丰富、方法多样的特点,有时候对题意的解读需要考生具有较强的理解能力,是高三学生数学学习和复习的重点、难点,也是考生确保取得优异成绩的突破口.
3 典题剖析
3.1 集合与常用逻辑用语
集合与常用逻辑用语是高中数学的基础,也是高考必考的内容,其中集合语言思想与常用逻辑用语可以渗透到高中数学的各个分支,与函数、方程、不等式等内容常常融为一体加以考查.
例1以A表示值域为R的函数组成的集合,B表示具有如下性质的函数φ(x)组成的集合:对于函数φ(x),存在一个正数M,使得函数φ(x)的值域包含于区间[-M,M].例如,当φ1(x)=x3,φ2(x)=sinx时,φ1(x)∈A,φ2(x)∈B.现有如下命题:
①设函数f(x)的定义域为D,则“f(x)∈A”的充要条件是“任意b∈R,存在a∈D,f(a)=b”;
②函数f(x)∈B的充要条件是f(x)有最大值和最小值;
③若函数f(x),g(x)的定义域相同,且f(x)∈A,g(x)∈B,则f(x)+g(x)∉B;
其中的真命题有_______(写出所有真命题的序号).
分析该题给出4个问题,内容丰富,解决问题的途径多样.第①问可根据函数的定义判断其正确性;第②问可通过举反例来判断其是错误的;第③问可通过f(x)的值域为R,g(x)在定义域是有界的,直接得到f(x)+g(x)∉B;第④问由对任意x∈R总存在常数M使得f(x)≤M,故知a=0,从而,于是f(x)∈B.
评注本题是以函数的有界性为背景,将集合、常用逻辑用语与函数融为一体的考题,所涉及的知识有函数的值域、函数的单调性等.其中集合的定义为学生题意的理解上设置了障碍,考查了学生的理解能力,通过结果的判断考查了学生的推理论证能力.
例2已知a,b,c为实数,f(x)=(x+a)(x2+bx+c),g(x)=(ax+1)(cx2+bx+1).记集合S={x|f(x)=0,x∈R},T={x|g(x)=0,x∈R}.若|S|,|T|分别为集合元素S,
T的元素个数,则下列结论不可能的是( )
A.|S|=1且|T|=0 B.|S|=1且|T|=1
C.|S|=2且|T|=2 D.|S|=2且|T|=3
分析因为方程x2+bx+c=0与方程cx2+bx+1=0的判别式Δ相等,所以当c≠0时2个方程根的个数是一致的.若方程x2+bx+c=0有不等的非零实根x1,x2,则方程cx2+bx+1=0有不等的非零实根,因此当a≠0且方程x2+bx+c=0有不等的非零实根时,有|S|=|T|;若a=0,且Δ<0,则|S|=1且|T|=0;若a≠0,且Δ<0,则|S|=1且|T|=1;若a≠0,且Δ=0,则有可能是|S|=2且|T|=2;若|T|=3,则a≠0,且Δ>0,此时一定有|S|.故选D.
评注该题以三次函数的零点为背景,将集合的概念与方程相结合,通过研究方程之间根的关系来考查集合中元素的个数,其关键是要注意2个方程x2+bx+c=0与cx2+bx+1=0(其中c≠0)根的一致性.同时,通过a=0和c=0等特殊情况的考虑,充分体现了对集合中元素确定性、互异性和无序性的理解.
3.2 函数的概念及性质
函数是中学数学中最重要的基本概念之一,其核心内涵是从非空数集到非空数集的映射,不仅是对集合学习的巩固和发展,更是学好其他知识的基础和工具.其中,学习的关键是对函数概念的理解,尤其是函数概念中“对应法则”的理解;对函数的单调性、奇偶性、周期性和对称性等性质的把握.
分析面对此题,学生或者是由内到外求出f(f(a))再解不等式,或者是由外到内通过f(f(a))≤2确定f(a)的范围进而确定a的范围,亦或是通过f(x)的图像直观地呈现f(f(a))与f(a)以及f(a)与a的关系,从而更简洁地发现a的取值范围.
解法1(由内到外)因为
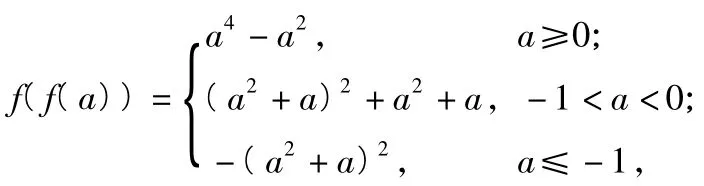
所以当a<0时,有f(f(a))≤2恒成立,而当a≥0时,有综上可知实数a的取值范围是
解法2(由外到内)当f(x)≤2时,有x≥-2,即
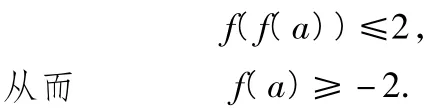
因此当a≥0时,有-a2≥-2,即,当a<0时,有a2+a≥-2恒成立,故实数a的取值范围是

图1
解法3(图像法)也可以通过函数图像直观地“读出”a的取值范围,如图1所示,当f(f(a))≤a时,有f(a)≥-2,当f(a)≥-2时,有
评注本题以分段函数为考查背景,考查学生对“f(a),f(f(a))”含义的理解.不同的思维、不同的方法,直接反映了学生对函数概念不同深度的掌握,此题与2009年浙江省普通高中数学会考卷第39题如出一辙.
例4设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2.若对任意的x∈[a,a+2],不等式f(x+a)≥2f(x)恒成立,则实数a 的取值范围是______.
分析本题将奇偶性和单调性融合在一起加以考查,其中根据奇偶性知

便于学生画出f(x)的图像,判断单调性.
解法1如图2,要使得f(x+a)≥2f(x)恒成立,必须将函数y=f(x)的图像向左平移,知a>0,因此当x∈[a,a+2]时有
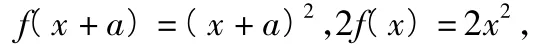
即x2-2ax-a2≤0在x∈[a,a+2]上恒成立.故可求得a的取值范围为
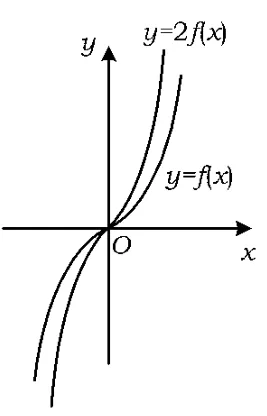
图2
评注本题作为2012年全国高中数学联赛试题第6题,虽然有一定的难度,但却将函数奇偶性和单调性综合在一起加以考查,是一道新颖灵巧的考题.其解答过程充分体现了图形在解决函数问题中的作用,也考查了学生对函数性质的深刻理解.
3.3 基本初等函数
高中数学中的基本初等函数主要包括二次函数、指数函数、对数函数和幂函数,其学习的重点是基本初等函数的定义、图像和性质,并能运用基本初等函数的图像与性质解决一些简单的问题.
例5设a>1,若仅有一个常数c使得对于任意的x∈[a,2a],都有y∈[a,a2]满足方程logax+logay=c,这时a的取值的集合为______.
分析方程logax+logay=c是一个不定方程,可视为函数问题加以分析解决.由已知得,且函数在 x∈[a,2a]上单调递减,从而函数的值域为,故即
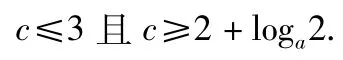
又因为常数c的值是唯一的,所以2+loga2=3,从而a的取值的集合为{2}.
评注本题考查数学中的转化思想,将已知条件“对于任意的x∈[a,2a],都有y∈[a,a2]”转化为“函数在 x∈[a,2a]上的值域是[a,a2]”,再利用不等式的“夹逼原则”求常数a的值,充分体现对学生数学素养的考查.
例6设f(x)=x2+(2a+1)x+a2+3a.若f(x)在区间[m,n]上单调递减,且值域为[m,n],求a的取值范围.
分析本题以一元二次函数为研究对象,考查学生对函数性质的理解,对学生问题的转化思想和分析解决问题的能力有着很高的要求.由题意知
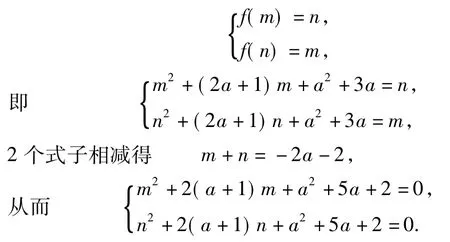
故问题可转化为函数

评注本题通过将已知条件转化为一元二次函数的零点问题加以处理,让陌生的问题熟悉化,其解答的策略主要在于对问题的等价转化,这是解决数学问题最核心的思想,也是考查学生数学素养的充分体现.
3.4 函数的应用
函数的应用以函数模型的应用为主线,以数学思想方法的渗透为主要学习意图,在研究函数的零点与方程的根的关系中渗透了函数与方程、数形结合和化归等思想,在建立确定性的函数模型解决问题的过程中渗透了数学建模、拟合的思想.因此,在高三复习中要贯彻这一教学意图,并注意学生的亲身体验.
例7已知f(x)=|x2-1|+x2+kx.若关于x的方程f(x)=0在(0,2)上有2个解x1,x2,求k的取值范围,并证明:
分析本题以含绝对值的一元二次函数为背景,考查方程有解问题.方程有解问题通常可转化为函数的图像与x轴有交点或转化为2个函数的图像有交点来处理,于是有如下解法.
解法1因为

可知函数f(x)的图像在(1,2)上与x轴至多1个交点,所以
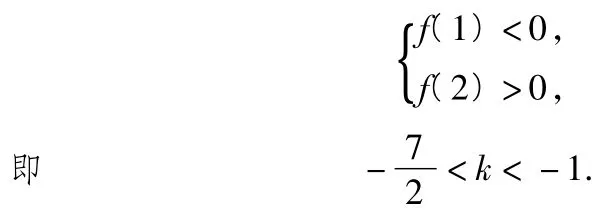
令函数f(x)的零点为x1∈(0,1),x2∈(1,2),则

解法2由f(x)=0,得
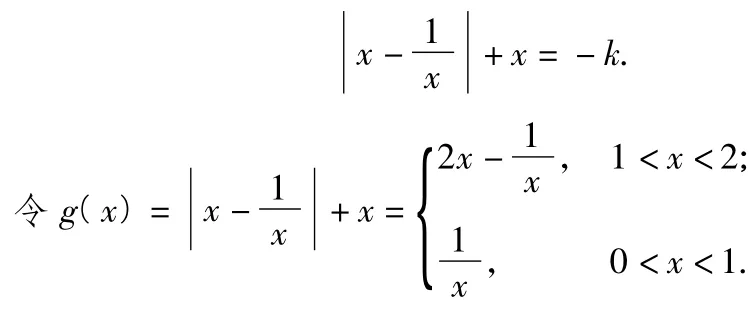
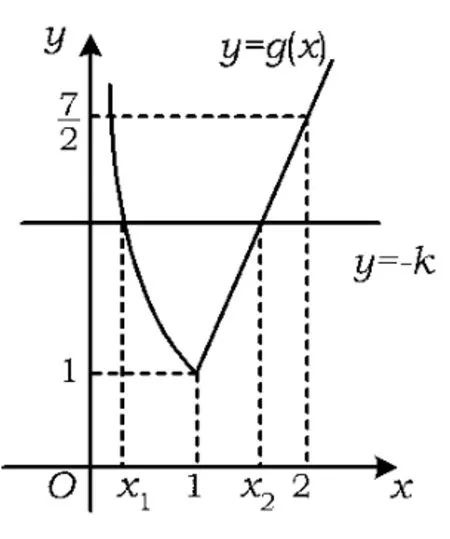
图3
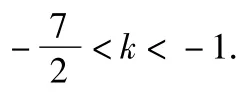
同时,易得
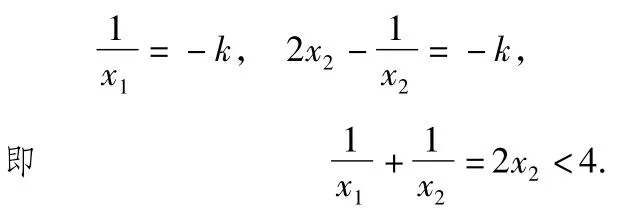
评注本题通过方程有解问题的研究,考查学生对函数与方程、数形结合和化归等思想的理解.其中函数与方程、数形结合和化归等思想是贯彻整个高中数学始终的,尤其是在函数问题中体现得最为充分,在高三数学学习中要特别关注.
例8某地区居民生活用电分为高峰和低谷2个时间段进行分时计价.该地区的电网销售电价如表1所示:
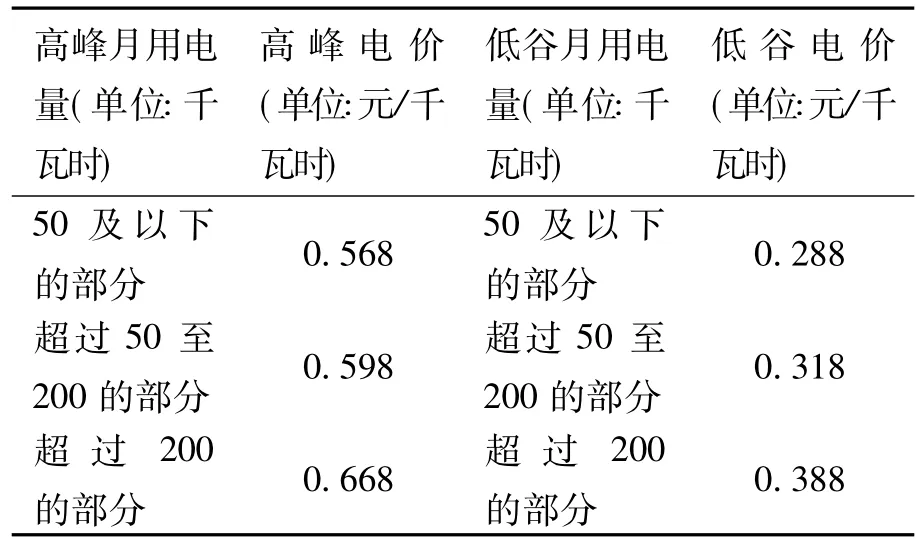
表1 用电价格表
若某家庭5月份的高峰时间段用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭本月应付的电费为______元(用数字作答).
分析此题的背景是学生较为熟悉的“峰谷电”问题,也是很多家庭为节约开支的用电形式,因此这是一个源自教材的分段函数模型问题.由于题中给出了具体的数据,因此学生能快速地进入“问题解决”状态,知道应付的电费应分2个部分:高峰部分为50×0.568+150×0.598;低谷部分为50×0.288+50×0.318.2个部分之和为148.4.
评注本题是对数学建模思想的考查,考查学生对题意的理解并能将其转化为数学问题来加以处理,充分体现了学生的数据图表处理能力.而今,计算原理、概率都已纳入了IB选修考查内容,因此函数这一应用值得关注.
3.5 函数的综合问题
函数综合问题是历年高考的热点和重点内容之一,一般难度较大,考查内容和形式灵活多样,要求考生在掌握有关函数知识的基础上进一步深化综合运用知识的能力,掌握基本解题技巧和方法,具备一定的推理转化和创新能力.
例9在xOy平面上有一点列P1(a1,b1),P2(a2,b2),…,Pn(an,bn),…,对每个自然数n,点Pn位于函数(其中0<a<10)的图像上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形.
1)求点Pn的纵坐标bn的表达式.
2)若对每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a的取值范围.
3)设cn=lgbn(其中n∈N*),若a取第2)小题中确定的范围内的最小整数,问数列{cn}前多少项的和最大?试说明理由.
分析本题是以函数图像上的点列为背景,以平面几何的性质为解题切入口,由点Pn在函数的图像上可得.由平面几何性质并结合数列{bn}的单调性知以bn,bn+1,bn+2为边长能构成一个三角形的充要条件是bn<bn+1+bn+2,故
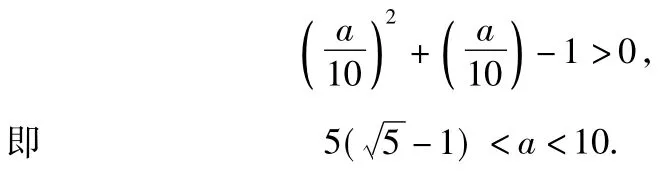
根据第2)小题a的取值范围可知a=7,从而
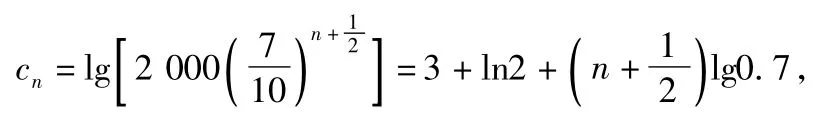
易知数列{cn}为一个递减的等差数列,且当cn=0时有n=20.8,故数列{cn}前20项的和最大.
评注本题采用了演绎推理的方法,通过函数的单调性来判断数列的单调性,突出了数列与函数的关系.
例10已知a>0,b>0,函数f(x)=ax-bx2.
1)当b>1时,证明:对任意x∈[0,1],|f(x)|≤1的充要条件是
2)当0<b≤1时,讨论:对任意x∈[0,1],|f(x)|≤1的充要条件.
分析本题是二次函数与绝对值不等式相结合的考题,重点考查学生的代数推理能力,其求解或证明的方法通常巧妙灵活,但从形入手是最为简洁、直观的方法.因为函数y=f(x)的图像为开口向下且经过原点的抛物线,所以可判断f(x)在x∈[0,1]上的最大值、最小值均为f(0),f(1),三者之一,故|f(x)|≤1对x∈[0,1]恒成立的充要条件为

当b>1时,|f(x)|≤1对x∈[0,1]恒成立的充要条件当时,|f(x)|≤1对x∈[0,1]恒成立的充要条件为即
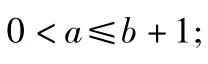
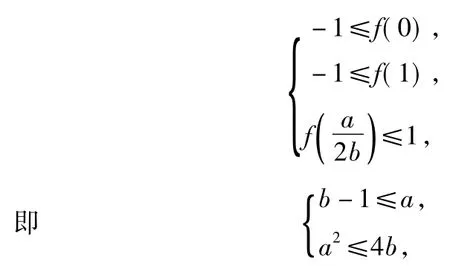
评注不等式恒成立问题的本质是对函数最值的讨论,而一元二次函数在闭区间上的最值只受到端点值和顶点值的影响.本题的解法牢牢地抓住了这一问题本质,将复杂的分类讨论过程变得简单快捷,体现了数学非同一般的简洁之美.
4 精题集萃
1.已知a1,b1,c1和a2,b2,c2均为正数,且不等式a1x2+b1x+c1>0和a2x2+b2x+c2>0的解集为A和B,则是“A=B”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分又不必要条件
2.已知函数f(x)=|2x-1|,g(x)=x2-(2+3k)x+ 2k+1,若函数y=g[f(x)]有3个不同的零点,则k的取值范围是( )
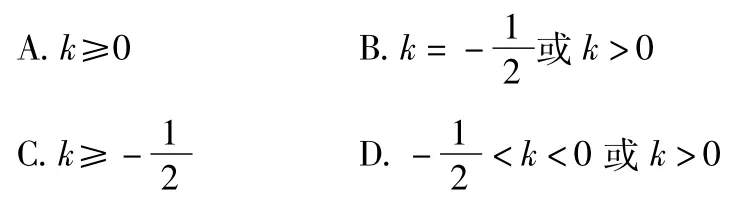
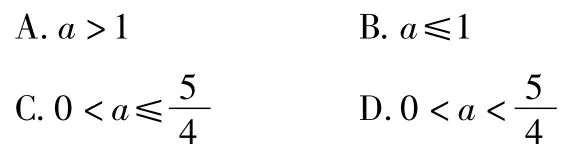
4.如果cos5θ-sin5θ<7(sin3θ-cos3θ),θ∈(0,π),那么θ的取值范围______.
5.已知f(x)是定义在R上且周期为3的函数,当x∈[0,3)时,.若函数y=f(x)-a在区间[-3,4]上有10个零点(互不相同),则实数a的取值范围是______.
7.对于c>0,当非零实数a,b满足4a2-2ab+4b2- c=0且使|2a+b|最大时,的最小值为______.
8.设a为实数,函数f(x)=x2+x|x-a|,x∈R.
1)若f(x)在R上具有单调性,求a的取值范围;
2)当a<0时,求f(x)在[-2,2]上的值域.
9.设二次函数f(x)=ax2+bx+1(其中a>0,b∈R),f(x)=x的2个根为x1,x2.
1)如果0<x1<2<x2<4,求f(-2)的取值范围;
2)如果x2-x1=2,且x∈[x1,x2]时,函数的最大值为M(a),求M(a)的表达式.
10.已知二次函数f(x)=x2+ax(其中a∈R).
1)若不等式f(2x-1)≥1-a对x∈R恒成立,求a的取值范围;
2)当a=2时,设n∈N*,,求证:
参考答案

