On the use of positive feedback for improved torque control

Houman DALLALI,Gustavo A.MEDRANO-CERDA,Michele FOCCHI,Thiago BOAVENTURA,Marco FRIGERIO,Claudio SEMINI,Jonas BUCHLI,Darwin G.CALDWELL

1.Department of Advanced Robotics, Istituto Italiano di Tecnologia (IIT), Genova, Italy;

2.Agile and Dexterous Robotics Lab,Institute of Robotics and Intelligent Systems,ETH,Z¨urich,Switzerland

On the use of positive feedback for improved torque control

Houman DALLALI1†,Gustavo A.MEDRANO-CERDA1,Michele FOCCHI1,Thiago BOAVENTURA2,Marco FRIGERIO1,Claudio SEMINI1,Jonas BUCHLI2,Darwin G.CALDWELL1

1.Department of Advanced Robotics, Istituto Italiano di Tecnologia (IIT), Genova, Italy;

2.Agile and Dexterous Robotics Lab,Institute of Robotics and Intelligent Systems,ETH,Z¨urich,Switzerland

This paper considers the torque control problem for robots with flexible joints driven by electrical actuators.It is shown that the achievable closed-loop tracking bandwidth using PI torque controllers may be limited due to transmission zeros introduced by the load dynamics. This limitation is overcome by using positive feedback from the load motion in unison with PI torque controllers The positive feedback is given in terms of load velocity,acceleration and jerk.Stability conditions for designing decentralized PI torque controllers are derived in terms of Routh-Hurwitz criteria.Disturbance rejection properties of the closed system are characterized and an analysis is carried out investigating the use of approximate positive feedback by omitting acceleration and/or jerk signals.The results of this paper are illustrated for a two DoF(degrees of freedom)system.Experimental results for a one DoF system are also included.

Force-torque control,load motion compensation,decentralized control

DOI10.1007/s11768-015-4146-y

1 Introduction

Enhancing the bandwidth of torque tracking is one of the challenges in building high performance legged robots.The problem of increasing the torque bandwidth cannot be resolved by using faster actuators but it is related to the load motion rather than the actuator dynamics.This issue becomes more critical when the load has little friction,i.e.,good bearings are used at the point where the load is attached to the transmission.In the robotics community,many publications on torque control have disregarded the load dynamics from the analysis[1-3]and this problem has been overlooked.

However, bandwidth limitations in force control problems using using hydraulic actuators have been reported in civil and automotive engineering.In[4],the interactionbetween the load motion and the actuator was shown for a hydraulic actuator.It was shown that a natural velocity feedback interaction path exists between the load(in that case a civil structure)and the actuator.Moreover,using a linearized model it was shown that the poles of the structure become the zeros of the open-loop force transfer function.As a result,if the structure is lightly damped,the actuators will be unable to apply a force at the natural frequency of the structure,regardless of actuator dynamics speed(bandwidth).In[4],it was shown that the problem is not due to the actuator dynamics but due to the structure(load)dynamics.In[5],experimental results of a car suspension test rig were reported where a conventional PID controller was incapable of producing appropriate force tracking and resulted in a significant phase lag at frequencies higher than 1Hz.The car test rig used very fast servo-valve dynamics to improve the force tracking performance but the problem was not resolved.In[6],the interaction between the hydraulic actuator and the structure is discussed and an intuitive positive velocity feedback scheme is proposed to compensate for the load motion by negating the effect of the natural velocity feedback.Despite simulation studies and experimental results,further analysis details on the effect of adding the positive feedback loop were not presented.Later in[7],several improvements were made to this method including the addition of phase adjustment to the positive velocity feedback.Also,the magnitude of the positive velocity feedback was underestimated to avoid potential instability.

In[8],motor torque control was considered using a disturbance observer while no load was attached to the motor.In this work we are interested in torque control at the joint and a system where the inertia is coupled via a compliant joint.

In[9],the authors showed how motion compensation can be applied to electrically and hydraulically actuated joints of a quadruped robot called HyQ[10].Their implementation ignored the electrical dynamics of the motor and the valve dynamics.Furthermore,the analysis was only carried for one degree-of-freedom joints.In[11],positive torque feedback was used to improve the problem of joint tracking,but it does not report the load motion problem.It was reported that positive joint torque feedback can compensate the detrimental effects of load torques on position tracking performance.However,with non-ideal torque sources,simple unity gain positive torque feedback can actually deteriorate the performance,or even result in instability.

Various complex control designs can be used for torque control.For instance,in[12]a combination of model based computed torque control,a state feedback and a nonlinear H∞was applied to a six DoF(degrees of freedom)robot manipulator with joint flexibility.A high performance torque control method was implemented on a light weight robot arm in[13].These methods need a good model and are implemented in centralized architectures which places additional requirements on real-time communication among various DoF.

In practice,the use of decentralized PI controllers is widespread in robotics.PI controllers are easy to tune but have limitations in terms of tracking bandwidth and disturbance rejection.The main idea in this paper is to use decentralized controllers by mitigating the existing limitations using quantified positive feedback.The source of these limitations will be fully characterized for multi-DoF systems in terms of multi-variable zeros.

The main contributions of this paper are as follows:The role of positive feedback is studied for mechanical systems driven with electric motors.It is shown that simple PI controllers can be used together with positive feedback to significantly improve torque tracking performance.Stability conditions for designing decentralized PI torque controllers,when the positive feedback is applied,are presented in terms of Routh-Hurwitz criteria.A two DoF simulation is used to illustrate the theory via root locus analysis and numerical simulations.Experimental results of a one DoF system are presented,validating the use of positive feedback.

The paper is organized as follows.Section 2,presents the system model and characterizes the corresponding multi-variable transmission zeros.Limitations on the achievable closed-loop torque bandwidth are explained in terms of the transmission zeros when using simple PI controllers.The use of positive feedback is introduced and it is shown that this can be designed to decouple the joint torque from the load dynamics.The positive feedback is given by three terms involving load velocity,acceleration and jerk.General results to investigate closed-loop stability when using this method are pre-sented in Section2.4.Section2.5,discusses disturbance rejection properties of the closed-loop system and in particular points out additional limitations when using PI torque controllers.In Section 3,a simulation study based on a two DoF model is used to verify the main results via nonlinear simulations and root locus analysis.In particular,the root locus analysis in Section 3.4 investigates the effects of using a partial positive feedback by neglecting load acceleration and/or jerk terms.Section 4 presents some experimental results for one joint of a robot leg prototype[14].Concluding remarks are given in Section 5.

Notation Throughout the paper,lower case letters are used for scalars,lower case and bold letters are used for vectors and uppercase letters are used for matrices.Moreover,subscripts L and m refer to load and motor,respectively.

2 System model and main results

This section presents the main results of the paper for the multi-DoF system given by

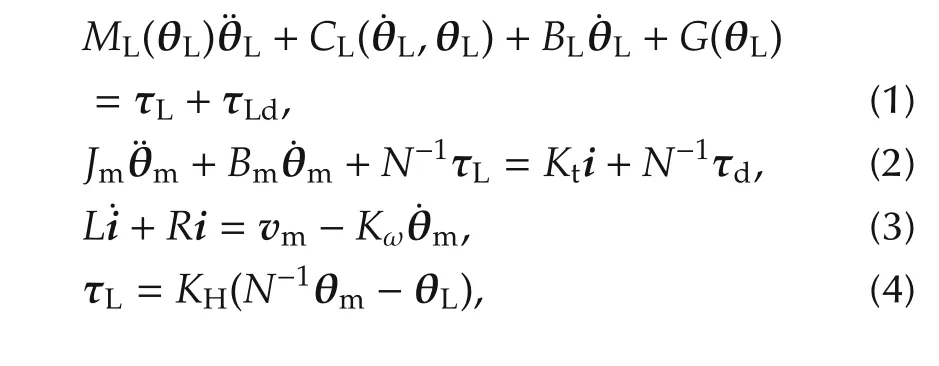
where θL,θm,˙θLand˙θmare the system states,namely angular positions and velocities of the load and motor in relative coordinates;τLdenotes the joint torque;τLdand τdare disturbances acting on the link and motor;i and vmare the motors current and voltage,respectively.The motor disturbance τdcan represent meshing friction and torque ripples produced by a reduction gearbox.The load disturbances τLdcan represent unknown collisions or interactions with the environment.We assume that the joint torque τL,the load and the motor positions are measured.Note however that one set of measurements is redundant since(4)provides a relation between them.A description of the system parameters is summarized in Table 1.The motor equations in the model correspond to aDC permanent magnet motor but as indicated by several motor manufacturers the same equations can be used for DC brushless motors whenever these are appropriately commutated.For the class of mechanical systems given by equations(2)-(4)all the matrices are diagonal and invertible.Linearizing(1)at a given load position with zero angular velocity yields

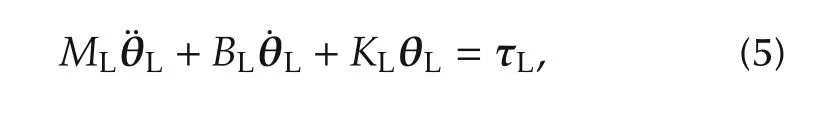
where MLis obtained by evaluating the mass inertia matrix at a given load position and the linearized gravity vector KLis obtained by evaluating the partial derivative of G at the given robot configuration.Linearized terms arising from CLbecome zero since we linearize around equilibrium with zero velocities.

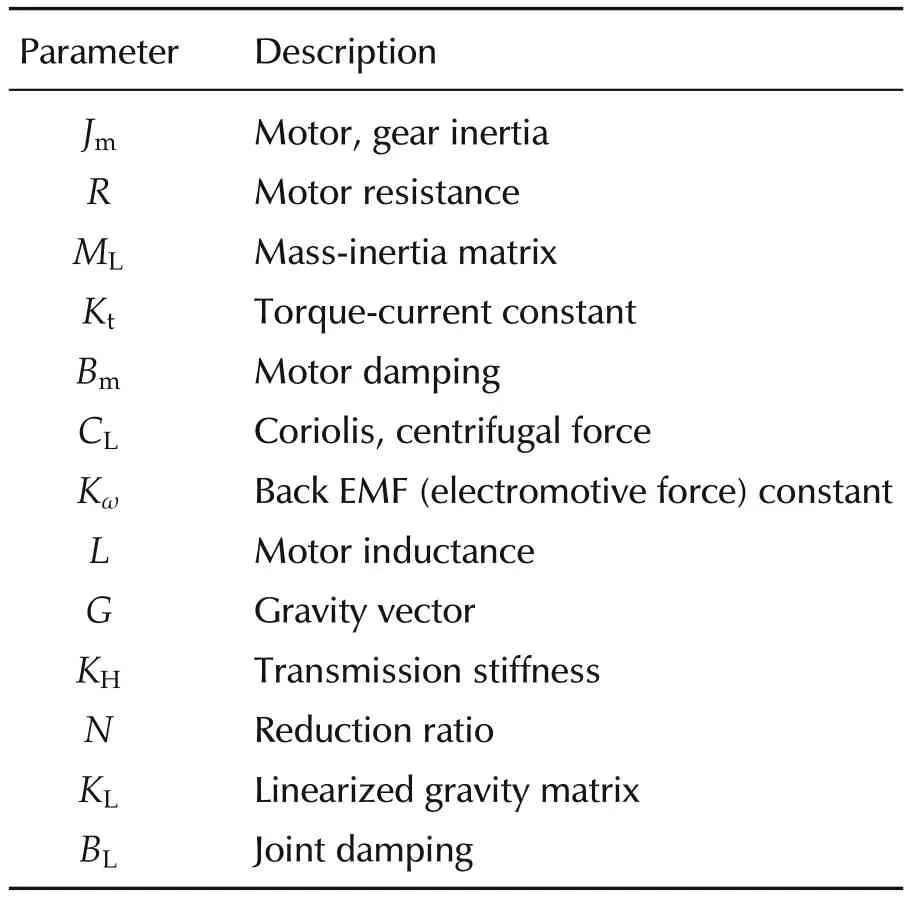
Table 1 System parameters.

Throughout the paper,the linearized model is used to investigate stability and disturbance rejection properties of the closed-loop system when a PI torque controller is combined with positive feedback compensation.The linearized analysis can be easily repeated for several configurations of interest by generating a suitable mesh of the robot workspace.In this manner the closed-loop performance of the robot can be investigated at different robot configurations.A nonlinear simulation will illustrate that the predicted performance using the linearized analysis can be reasonably close to the results obtained via nonlinear simulations.The following result presents an important property of the linearized system.

Lemma 1(Multi-variable transmission zeros)Consider the linearized system given by(5)and(2)-(4)and define ΛL(s)=MLs2+BLs+KL.

The transmission zeros from the motor voltage to the joint torque are given by the roots of the polynomial det(ΛL(s))=0.

Proof See Appendix A1.

Lemma 1 has substantial implications on the achievable closed-loop performance of a torque control system when using PI torque controllers.Consider the case when BLand KLare positive definite matrices then the transmission zeros lie in the left half plane.If the damping BLis very small then these zeros will be close to the imaginary axis and the PI controller poles at the origin will be attracted towards these zeros.Hence,closed loop poles near the imaginary axis arise and these poles have slow transients therefore the closed-loop system has a low bandwidth.These effects will be illustrated in Section 3.2 for a two DoF example.When KLis not positive definite then some transmission zeros appear in the right half plane(non-minimum phase zeros).In addition,in this case the open-loop system is also unstable.In general this type of systems are more difficult to control[15]and further discussions are given for the two DoF simulation in a later section.

2.1 Positive feedback compensation

It is well known that use of positive feedback can destabilize a system.In linear systems it can shift poles from stable to unstable regions.However,positive feedback can also be used to enable pole-zero cancellations in the stable region.This section introduces the idea of positive feedback compensation and shows how by suitable design,it can decouple the load motion from the joint torque dynamics,to improve the bandwidth limitations.

Lemma 2 Consider the linearized system(5)and(2)-(4)and introduce the feedback vm=F(s)θL+vr,where vris the reference voltage.The corresponding linear closed-loop system is given by

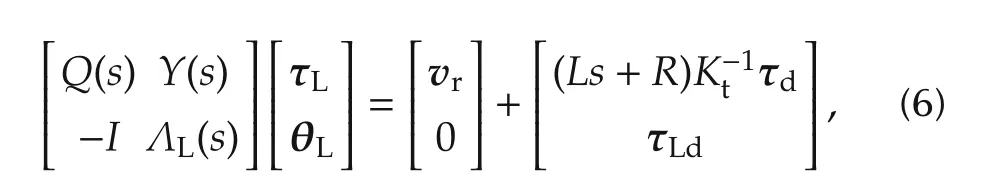
where I is an identity matrix and

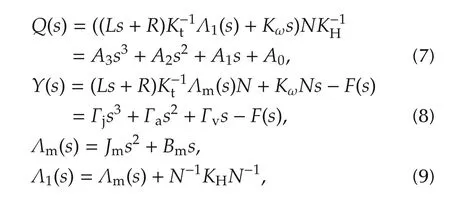
where

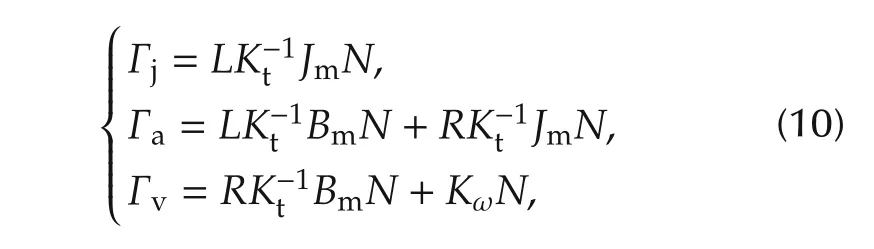
and

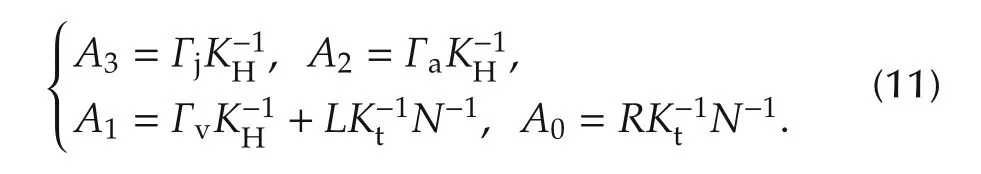
ProofSee Appendix A2.

A block diagram representation of(6)is shown in Fig.1.Inside the dashed box we have the intrinsic feedback in the system and the outer positive feedback loop can be chosen to cancel out the intrinsic feedback.From Lemma 2 by selecting F(s)such that Y(s)=0,the joint torque τLis decoupled from the load dynamics.

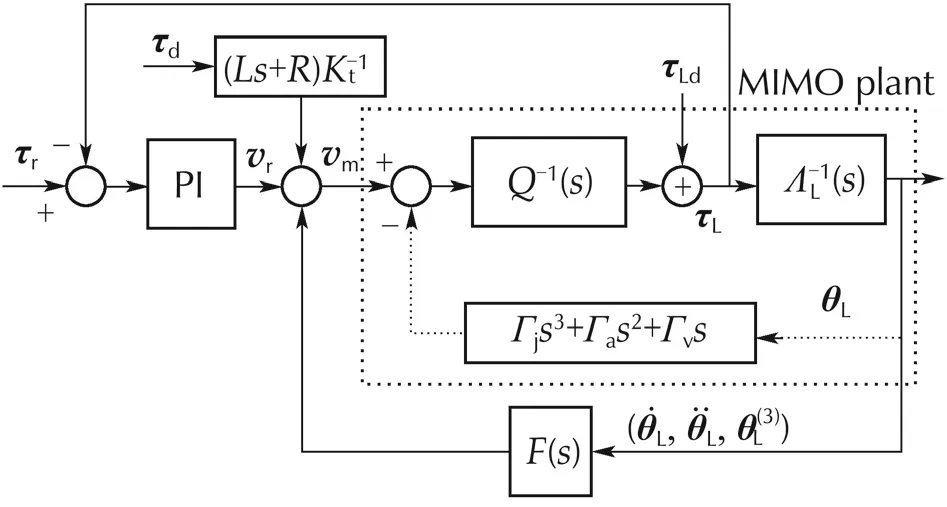
Fig.1 Control block diagram for linearized system,where τr denotes the input reference torque,and F(s)is the positive velocity feedback gain.

Lemma 3(Positive feedback compensation)The feedback

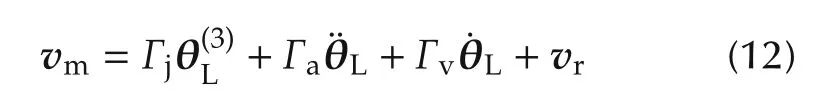
decouples the joint torque τLfrom the load dynamics.

Proof This is a direct consequence of Lemma 2.Setting Y(s)=0 in(6),solving for F(s)and taking inverse Laplace transforms yields(12).

Note that in(6)the matrix on the left hand side becomes lower triangular for the feedback(12)since Y(s)=0.This implies that the load dynamics are unobservable from the joint torque and the multivariable transmission zeros are cancelled by the load dynamic poles.

In addition,the feedback compensation(12)only depends on the drives parameters and since these matrices are diagonal(12)is a decentralized feedback assuming that the velocities, acceleration and jerk signals are available.Furthermore,the matrix Q(s)is also a diagonal matrix that only depends on the drive parameters.

The feedback matrices Γj,Γaand Γvonly depend on motor and transmission matrices as shown in(10)and since KH,N,Jm,Bm,L,R,Ktand Kωare all diagonal,invertible and positive definite,Γj,Γaand Γvalso have the same property.

Remark 1 The results in Lemmas 2 and 3 can be obtained without using the linearized equation(5).The derivation can be carried out entirely in the time domain but it becomes a little more elaborate.Therefore for the nonlinear system,the positive feedback compensation(12)also decouples the joint torque τLfrom the load dynamics.

The next section considers the design of a PI torque controller.

2.2 PI control and positive feedback

Once the feedback compensation is implemented we introduce a decentralized PI torque controller given by

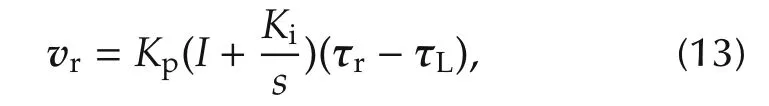
where Kpand Kiare diagonal matrices,and τris the reference torque.

Lemma 4 Consider the system in Lemma 2 and the PI torque controller(13).The closed-loop system is

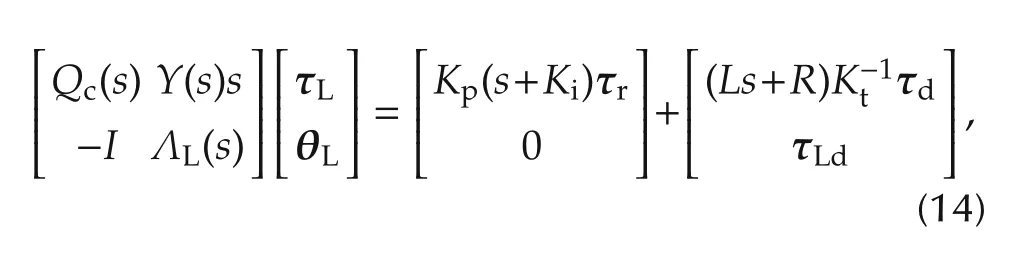
where

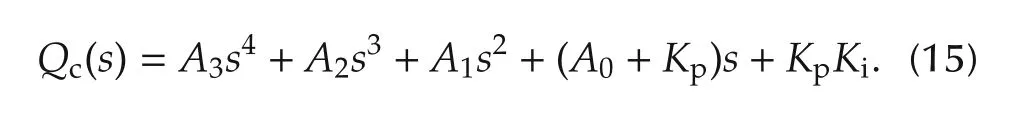
Proof From Lemma 2,substituting(13)in(6),the result follows after some standard algebraic calculations. □

Lemma 4 will be used in subsequent sections to determine closed-loop stability for any given PI controller and any feedback compensation as in Lemma 2.

2.3 Real-time implementation requirements

Implementation of the feedback compensation(12)requires velocity,acceleration and jerk signals which are not measured.In general,the acceleration and jerk(Γa,Γj)feedback terms cannot be discarded since the system(14)can become unstable even if Qc(s)is asymptotically stable.A result for investigating stability when acceleration and/or jerk feedback are ignored is given in Section 2.4 and further discussions are presented in Section 3 for a two DoF example.In the experimental Section 4,load’s velocity,acceleration and jerk are computed on line and used for full load motion compensation.

The velocity,acceleration and jerk signals required in(12)can be obtained via robust numerical differentiators.Relevant publications in this topic are[16],[17]and[18].In[19],an application is considered where numerical differentiation is used to determine acceleration.In[20],the authors present a nonlinear velocity estimator.Reducing noise in the measurements can be accomplished using high resolution position encoders and filtering to obtain approximate derivatives,as used in the experimental results in Section 4.

An alternative to numerical differentiation is to use the system model.From the nonlinear equation(1)we can obtain the load acceleration and jerk signals

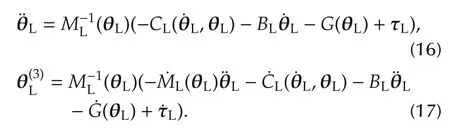
In(16)and(17),the load disturbance τLdhas been neglected since this is not known.Neglecting the disturbance can have some degradation in performance but does not affect stability.Estimation of load acceleration and jerk also requires knowing the Coriolis,gravity and dynamic parameters of the system accurately.Furthermore,(16)and(17)incorporate all the load interactions and can be implemented as a centralized scheme.For the linearized analysis acceleration and jerk signals can be computed from(5),also ignoring the load disturbance τLd

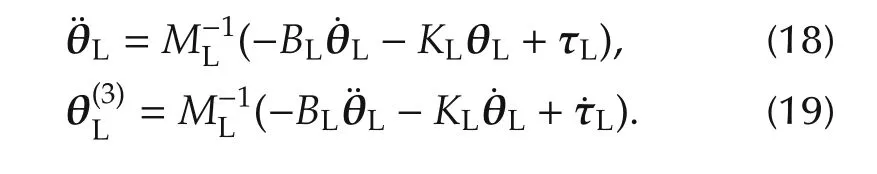
In this case,(18)and(19)can also be written as feedback in terms of system states,(θm,θL,˙θm,˙θL)or(τL,θL,˙τL,˙θL).

2.4 Stability analysis

This section,first considers the stability of the closed loop system in Lemma 4 when the positive feedback compensation is chosen as in Lemma 3 so that Y(s)=0.The second result in this section is derived to determine closed-loop stability of the system when the positive feedback compensation is partially implemented.

Lemma 5 Consider the closed-loop system in Lemma 4 with the feedback compensation in Lemma 3,then the closed-loop torque response is given by

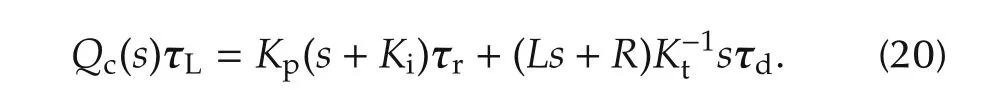
Proof From(14)setting Y(s)=0. □

Since all the matrices in(20)are diagonal,the system reduces to a set of uncoupled single input single output systems and Qc(s)=diag{qc1(s),qc2(s),...,qcn(s)}where each polynomial qci(s)=a3is4+a2is3+a1is2+(a0i+kpi)s+kpikiiand all the scalars kpi,kii,a3i,a2i,a1iand a0iare positive.From the Routh-Hurwitz array,conditions for stability of Qc(s)are

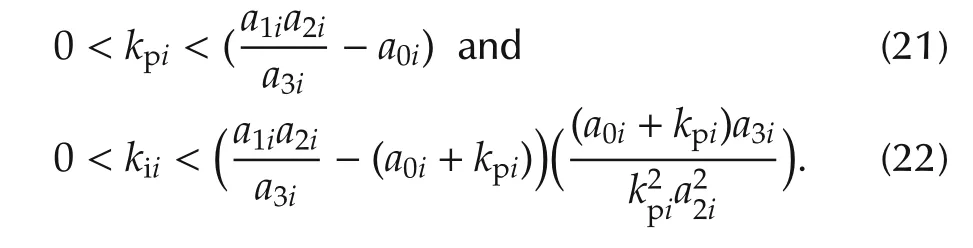
These inequalities give a range of values for the controller gains kpiand kiiensuring closed-loop stability.

The second result in this section is useful for investigating stability when the full compensation in Lemma 3 is not implemented for example to determine if the terms involving jerk and acceleration can be neglected.

Consider the PI torque controller(13)and the feedback compensation

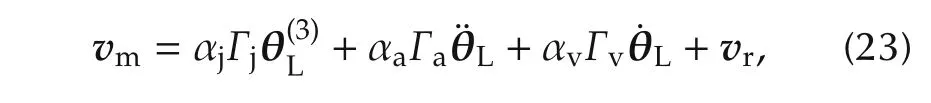
where the coefficients Γj,Γaand Γvare defined in(10)and αj,αaand αvare scalars between[0,1].The closed loop system is given by

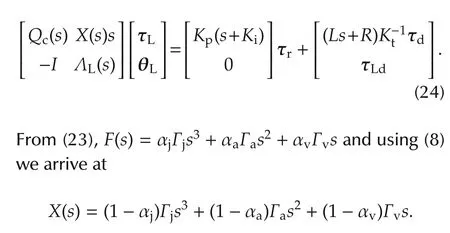
Lemma6 The closed-loop characteristic polynomial of (24) is given by

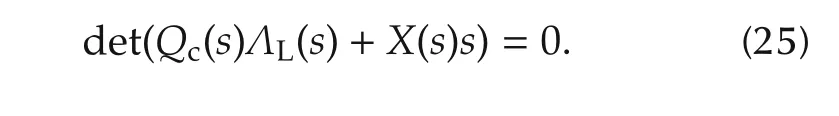
Proof From(24),the determinant of the block partitioned matrix is However,det(Qc(s))det(Q-1c(s))=1 and this gives(25). □

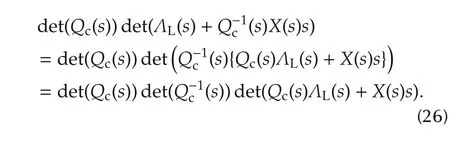
Remark 2 Expanding(25)in powers of s we can obtain a state space realization of(Qc(s)ΛL(s)+X(s)s)in terms of block companion matrix and compute the corresponding eigenvalues to determine stability of the closed-loop system(24).The block companion form is given in Appendix A3.

2.5 Disturbance rejection

This section provides the main result to asses the disturbance rejection properties of the closed-loop system with a PI torque controller for both the full positive feedback compensation and a partial compensation.The disturbances of interest are τdthose occurring at the motor since these can represent nonlinear friction and torque ripples in the gearbox.

Lemma 7(Disturbance transmission)1)For the closed-loop system in Lemma 5 with full feedback compensation the transfer function matrix from τdto the joint torque τLis

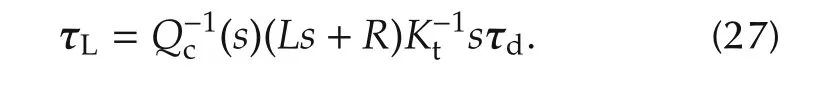
2)For the closed-loop system(24)with a partial feedback compensation the transfer function matrix from τdto the joint torque τLis

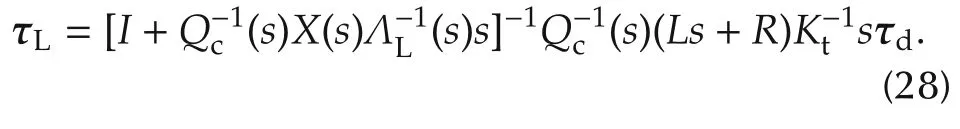
Proof Equation(27)in part 1)follows easily by setting τr=0 in(20).For(28)in part 2)setting τr=0 in(24)and using the inverse of a block partitioned matrix we have

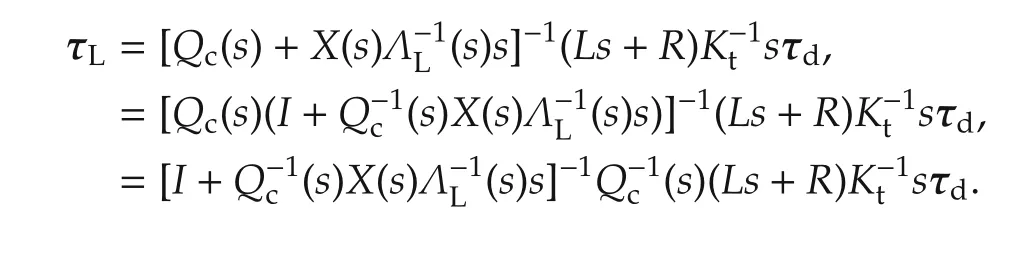
From(27)and(28),the disturbance rejection properties of the linearized system can be displayed via the relevant frequency response plots.This will be illustrated in Section 3 for the two DoF example.

3 Simulation results

In this section,a two DoF nonlinear simulation is used to show the improved torque performance with PI controllers combined with the positive feedback(12).Model parameter values are given in Section 3.1.Nonlinear simulations are presented in Sections3.2 and 3.3,while Section 3.4 discusses how the load stiffness KLaffects the transmission zeros.Also,the effects on closedloop stability when ignoring jerk and acceleration in the positive feedback are investigated.It is shown that to maintain stability jerk and acceleration feedback terms in general cannot be discarded except for some particular cases.

3.1 Model and controller descriptions

Parameter values for the two DoF model are provided in this section.The mass-inertia matrix ML,Coriolis CLand gravity G vectors are given in relative coordinates:

The linearized gravity matrix at θLis

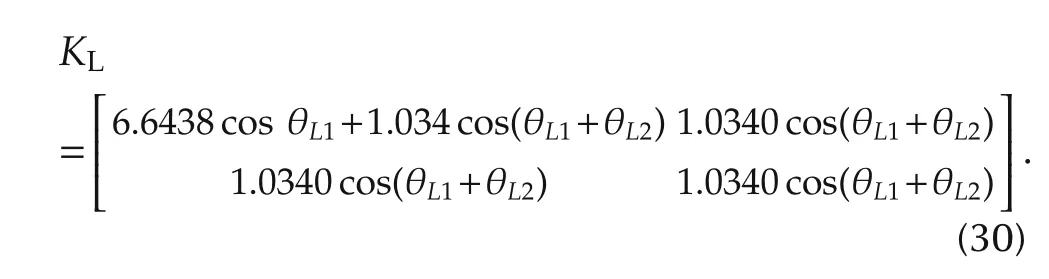
Substituting the operating point θL=[0 0.5]Tand ˙θL=[0 0]Tin the linearized model(29)and(30)yields

The analysis can be repeated at other operating points θL.Identical drives are used for each DoF in this system.A harmonic drive gearbox with stiffness KH=912I(N·m/rad)and reduction ratio N=150I.A motor with inductance L=3.2×10-4I(H),resistance R=0.664I(Ω),torque constant and back EMF constant Kt=Kω=0.041I(V·s/rad).The total drive inertia,Jm=1.387×10-5I(kg·m2)and damping Bm=1.996×10-5I(V ·s/rad).The load damping is BL=0.01I(V ·s/rad).

Decentralized PI torque controllers were designed using the result in Lemma 5 and the Routh-Hurwitz inequalities(21)and(22).Fig.2 shows the stability region for the controller gains,where the maximum value for kpis 14.In addition,the controller gains were also selected so that the closed-loop system without positive feedback is also stable.The controllers are given by

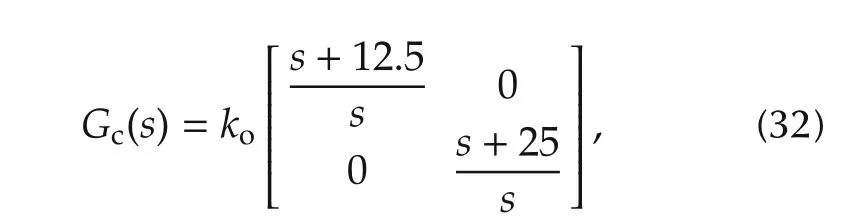
where ko∈[0,6].The controller gain ko=2 is chosen to achieve a closed-loop torque bandwidth of 50Hz(settling time of about 45ms)and overshoot of 30%at each joint after applying the positive feedback(12).

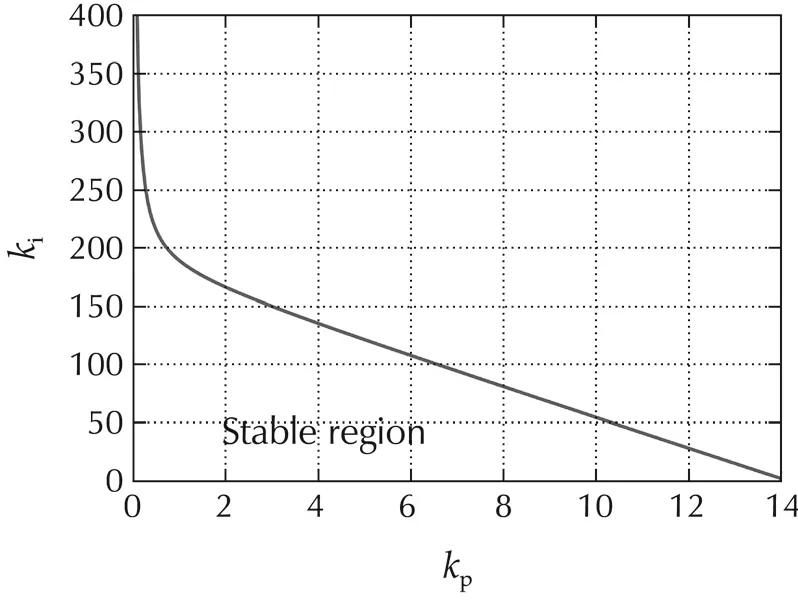
Fig.2 Stability region for the PI torque controller gains.

3.2 Nonlinear simulation results

This section presents simulation results comparing the closed-loop performance with and without positive feedback for the PI torque controller(32)and ko=2.Equations(16)and(17)are used in the nonlinear simulations to compute the load acceleration and jerk terms in the positive feedback.

Fig.3shows closed-loop simulation results of the nonlinear system for a torque step command of τr=[3 0]T.A fast response is achieved with positive feedback compensation as seen in the left hand side plots in Fig.3 while the step response shown in the right hand side without the positive feedback has a long transient and is oscillatory.It is evident that the positive feedback has considerably improved the torque tracking bandwidth.However,Fig.4 shows that the control signals for the system with positive feedback are more responsive to load motion.

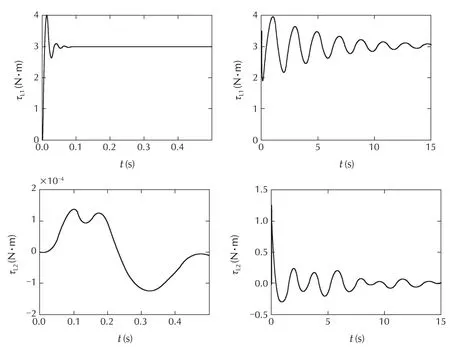
Fig.3 Torque step responses of nonlinear closed-loop system with positive feedback(left)and without positive feedback(right).

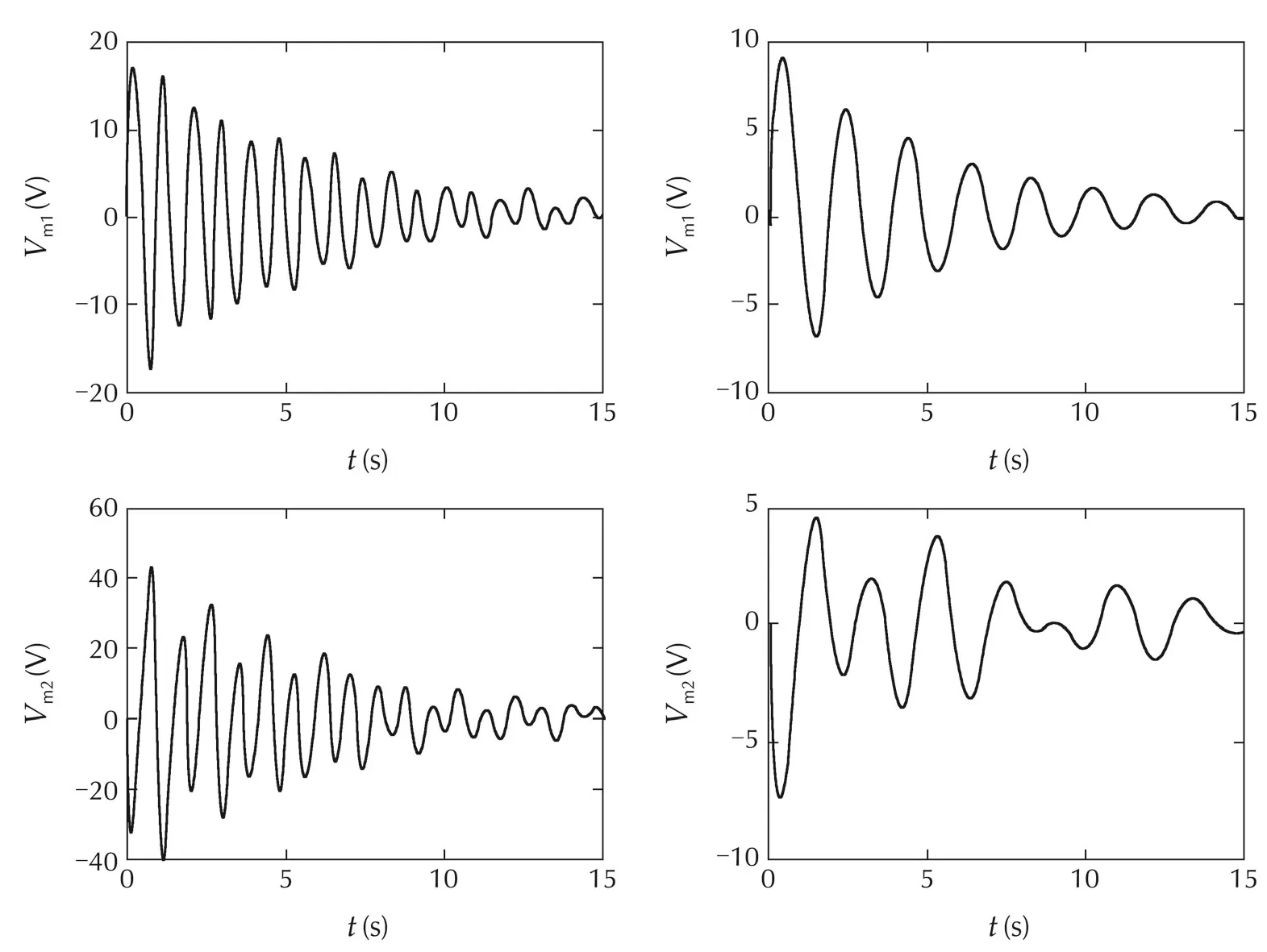
Fig.4 Motor voltages for torque step responses of nonlinear closed-loop system with positive feedback(left)and without positive feedback(right).

3.3 Disturbance rejection

In this section,the disturbance rejection properties of the proposed controller are analyzed in terms of bode plots for the closed-loop system using the results from Lemma 7.In particular it is shown that the linearized analysis can predict with reasonable accuracy the amplitudes of oscillations caused by cyclic friction τdat the motor input.The predicted amplitudes match well the oscillations observed in nonlinear simulations.In general,nonlinear friction and torque ripples cause undesirable effects in the closed-loop response of mechanical systems which may be reduced by increasing the bandwidth of the closed-loop system or designing suitable friction compensation schemes. In particular, torque ripples or cyclic friction in gearboxes give rise to oscillations[21,22].These disturbances are then propagated throughout the system.

Fig.5 shows the step response nonlinear simulation of the closed-loop system with cyclic friction included in both motors. The torque reference for joint one is3N·m and zero for joint two.Full positive feedback is applied together with the PI torque controller.The RMS torque errors are 0.0961N ·m and 0.0725N ·m for the first and second DoFs respectively.The torque ripple used at the input of the motors is τd=0.013cosN·m,where φ = π for joint one and φ = for joint two.The amplitude and phase of the torque ripples were estimated from experimental data for a drive mounted on a single joint system and corresponds to the fundamental frequency of the ripples arising in the harmonic drive[21].Similar models for cyclic friction have been reported in[22]for other types of gearboxes.

The bode plots in Fig. 6 show how the disturbances τdaffect the joint torque.The worst case is the resonance at35Hz while all other frequencies are attenuated much further.

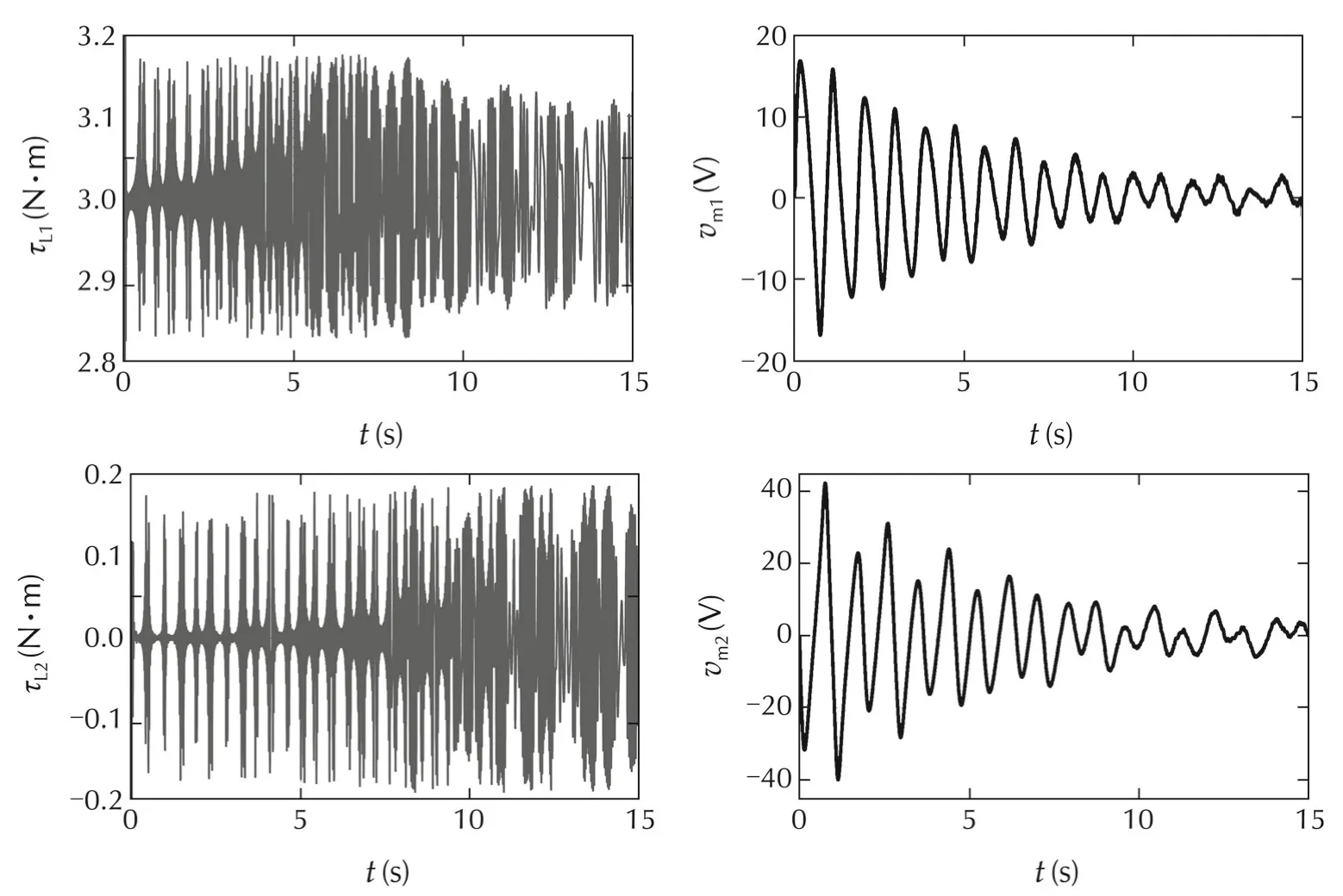
Fig.5 Joint torque step response with torque ripple disturbance and the corresponding control input for a two DoF system.

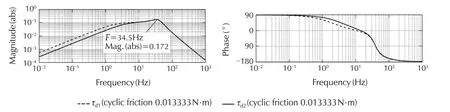
Fig.6 Bode plot of joint torque with torque ripple disturbance for the two DoF system.The peak magnitude is about 35Hz.

Note that the peak amplitude in the bode plot predicts quite well the oscillation peaks in the nonlinear simulation shown in Fig.5.The power spectral density of the torque oscillation errors due to cyclic friction is shown in Fig.7.

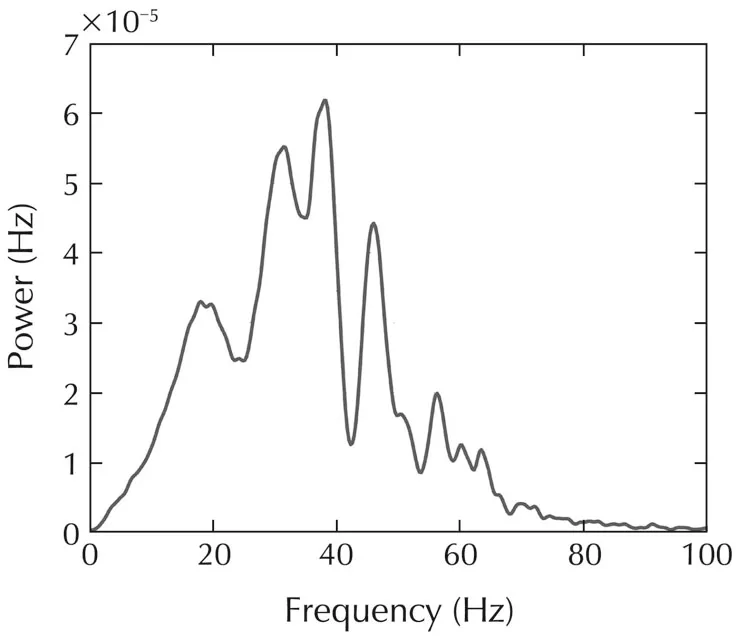
Fig.7 Power spectrum of joint torque error response for the two DoF system.The peak magnitudes occur around 35Hz.

The figure clearly shows that peak values occur in the frequency range 30-40Hz which is in the neighborhood of resonant peak in the bode plot.

3.3.1 Resonance compensation

There are several options to reduce the effect of torque ripples,for example using lead or notch com-pensators in cascade with the PI controllers.For the nonlinear simulation shown in Fig.8,a lead compensator G(s)=is added in cascade with

LCthe PI controller. The simulation clearly shows a substantial reduction in the peak amplitude of the oscillations to about 0.1.The RMS torque errors have been reduced to 0.0640N ·m for joint one and 0.0391N ·m for joint two.The resulting bode plot in Fig.9 also shows the effectiveness of the lead compensator which has attenuated all the magnitudes to less than 0.091.

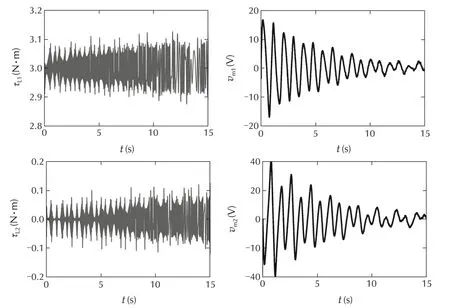
Fig.8 Joint torque step response with torque ripple disturbance and the corresponding control input with lead compensation.

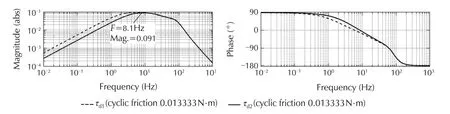
Fig.9 Bode plot of joint torque with ripple disturbance for the two DoF system with lead compensation.

Stiction is another disturbance which is present in torque control problem.Fig.10 shows the effect of stic-tion before and after lead compensation.The simulations show that also the effects of stiction are reduced for the controller with the lead compensator.If disturbance rejection cannot be improved with PI controllers and simple additional compensators then more complex controllers are needed.This highlights some limitations when using PI control.

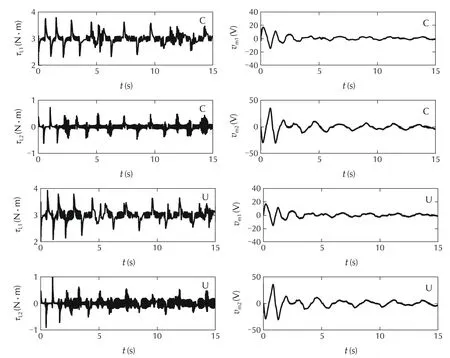
Fig.10 Torque step responses of lead compensated(C)and uncompensated(U)system with cyclic friction and stiction.

3.4 Transmission zeros and approximate positive feedback

This section first considers how load stiffness KLand damping BLaffect the transmission zeros location in the complex plane.Then the effects of approximate positivefeedback on pole-zero cancellations and closed-loop stability are investigated,in particular when the load acceleration and jerk terms in the positive feedback are neglected.

3.4.1 Effect of load stiffness and damping on transmission zeros

This section presents a discussion regarding load stiffness KLand damping BLeffects on the multivariable zeros.The two DoF simulation is used to illustrate these effects numerically.Throughout it is assumed that BLis positive definite.Since in a physical system damping is always positive and in general BLis a diagonal matrix.

First,consider the case when the load stiffness is positive definite,KL＞0.In this case the transmission zeros will always lie in the open left half plane and when damping is small these zeros will be located near the imaginary axis.For the linearized system(31)there are four transmission zeros,the roots of det(ΛL(s)=0),located in complexpairsat-0.0304±j3.0036and-0.2037±j7.4767.As BLincreases the zeros move towards the real negative axis.For the simulation setting BL=diag{0.8,0.4}there are two complex zeros-0.9408±j3.3033 and two real zeros at-2.4747 and-17.29.

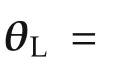
An alternative is to consider gravity compensation methods to remove the gravity torque G in the nonlinear system.Gravity compensation methods for systems with flexible joints have been investigated in[23,24]and are based on the desired gravity compensation(in terms of the desired load position)or using a motor biased compensation.However,these methods are only approximate and do not completely remove the gravity torques.Methods employing the actual load position for gravity compensation could be used but these have not been studied in detail and at present we cannot ensure that this is a suitable approach in conjunction with the positive feedback scheme for torque control,particularly for systems that give rise KLbeing indefinite or negative definite.This question is left open for future research.Therefore when KL≤0 the positive feedback compensation does not seem to be a suitable strategy for torque control.

3.4.2 Effect of approximate positive feedback on stability

This section considers the effect on closed-loop stability when using approximate implementations of the positive feedback compensation for the two DoF simulation.In particular, we investigate the effects on closed-loopstability when ignoring terms involving load acceleration and jerk.

First,consider the positive feedback in(23)and let α = αj= αa= αv,where α takes values in the interval[0,1].In this analysis the acceleration and jerk are computed from equations(18)and(19)written in state feedback form.For α=0,there is no positive feedback applied while for α=1 the full compensation is used.For intermediate values of α,a partial positive feedback compensation is implemented.The closed-loop poles are given by the roots of the characteristic polynomial in Lemma 6.As α varies,Fig.11(a)and(b)show the root locus of the closed-loop poles for the two DoF system and the PI controller gain k0=2 in(32).The position of the transmission zeros are shown as circles and the poles are shown as crosses.Fig.11(a)displays the root locus in the vicinity of the transmission zeros and for α=1 four poles cancel the four zeros.Fig.11(b)shows an overall view of the root locus.From this analysis we conclude that the closed-loop two DoF system with the PI controller remains stable for all α∈[0,1].

Second,in terms of approximate implementation,consider neglecting the jerk term,where αa= αv=1 and αj=0 in(23).Using Lemma 6,the effect of discarding jerk feedback can be investigated.For the two DoF system ignoring the jerk term does not produce an unstable closed-loop system.This result can also be verified for the nonlinear system via a simulation.

This conclusion does not hold in general and we next provide an example showing that without jerk feedback instability can arise.For example,consider a motor with an inductance L=3.2I(mH)(ten times lager than before),varying the PI gains ko∈[0,6].We arrive at a conditionally stable system1Conditional stability:A conditionally stable system switches between stable an unstable operation as the loop gain is changed..Stability without jerk feedback could be recovered for sufficiently large damping,e.g.,BL=diag{0.1,0.1}.In summary,when KL＞0,there are cases in which jerk feedback cannot be discarded and Lemma 6 can be used to investigate this issue.

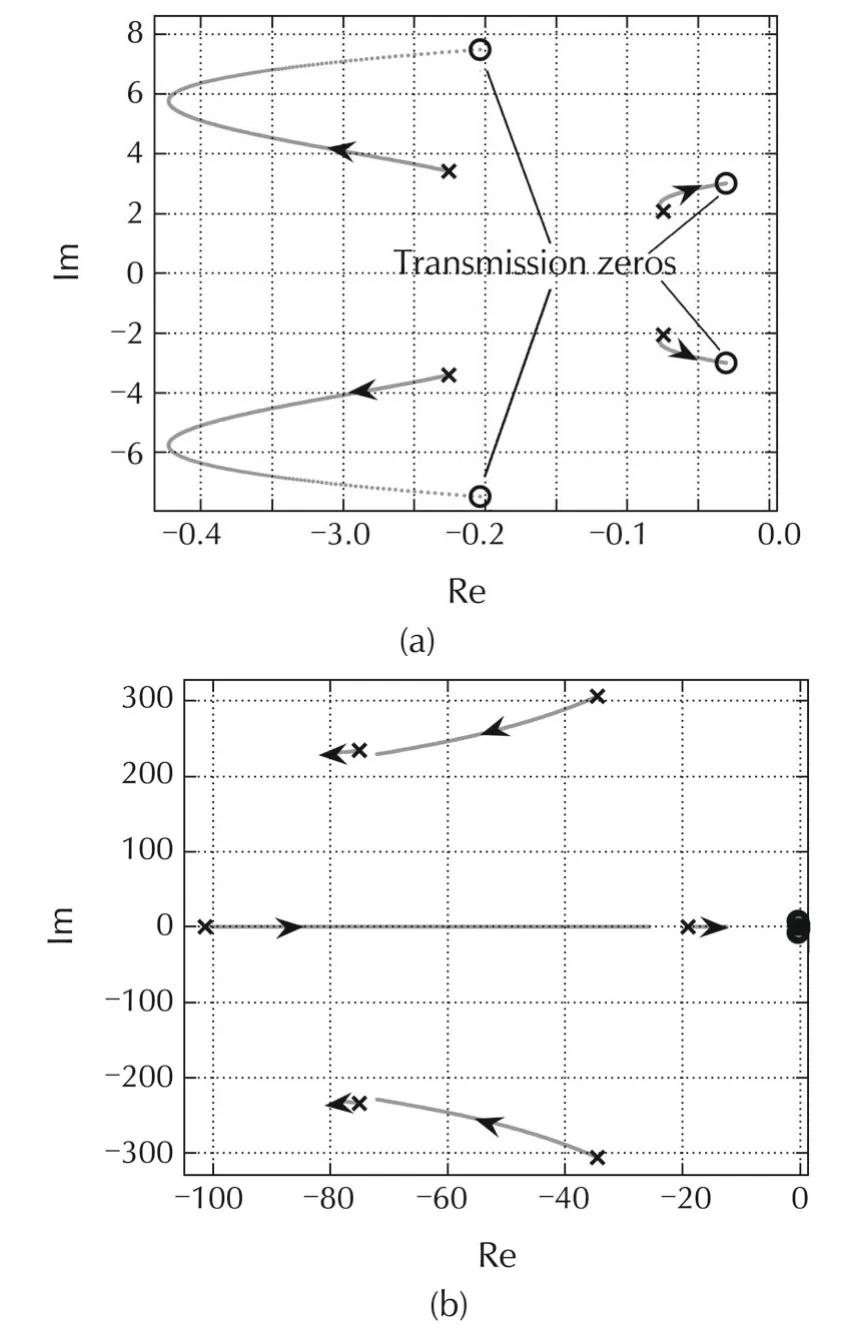
Fig.11 Root locus plot as the positive feedback varies,α∈[0,1],for the PI controller gain k0=2.(a)Zoom on the transmission zeros.(b)Overall view of the root locus.

When the load stiffness KL=0,numerous nonlinear simulations without jerk feedback have not shown stability problems.However,a proof for this conjecture is left as an open question.Recall that for KL=0,the transmission zeros lie on the real negative axis as opposed to the complex zeros presented in Section 3.4.1.It seems that in this situation it is easier to compensate the effect of load motion without jerk feedback.

Finally, consider the case that both jerk Γjand acceleration Γaterms are neglected,i.e.,αv=1 and αa= αj=0 in(23).Using Lemma 6 for the two DoF simulation,when KL＞0 and BLis very small results in conditional stability.When BLis sufficiently large,for example if BL=diag{0.8,0.4},then the close loop system without acceleration and jerk feedback remains stable.Also,when KL=0 the system without acceleration and jerk feedback appears to remain stable.This conjecture is left open for future research.

3.4.3 Effects of sampling, noise, filtering and friction on performance

In order to investigate the effects of sampling,quantization noise on sensors,filtering and friction on performance,the nonlinear simulations are performed with discrete time control and filters to replicate and understand the effects seen in experiments.

Fig.12(a)shows the result of a continuous time control of the nonlinear system.Comparing Fig.12(a)and(b),we see that sampling alone causes performance degradation,then Fig.12(c)shows adding quantization causes further degradation.Comparing Fig.12(a)and(b),we see the effect of load damping on torque tracking which improves the response.Filtering is used in Fig.12(d)to mitigate the effects of quantization but still the performance is degraded.A third-order Butter worth filter with cut-off frequency of 150Hz is used.Fig.12(e)and(f)show when adding cyclic friction and stiction,the performance is worse but it is more difficult to discriminate the effects of filtering.Two sinusoidal signal with amplitude of 0.013 and phase difference of 90°are used to add cyclic friction disturbance to the system,as shown in Fig.12(e).Lugre friction model is used to simulate the nonlinear behavior of stiction in Fig.12(f).The effects shown in Fig.12(f)are present in the experimental results.

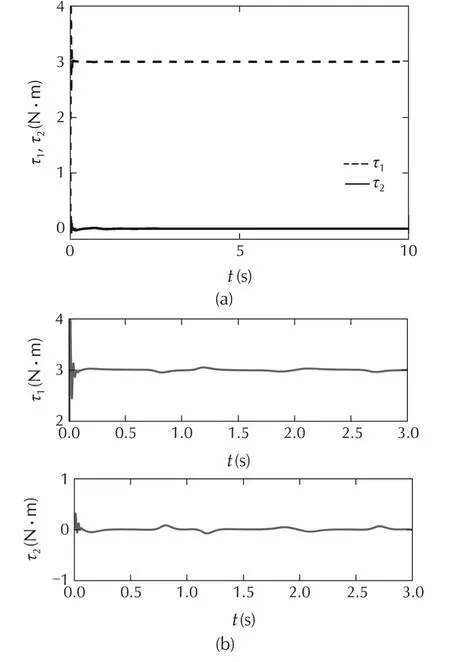
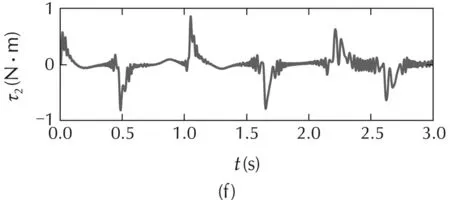
Fig.12 Effects of sampling,quantization,filtering,cyclic friction,stiction and BL=0.01 on torque control.

4 Experimental results

The proposed positive feedback and lead compensation was implemented on the robotic prototype leg presented in[14],and shown in Fig.13 to verify the theoretical results.

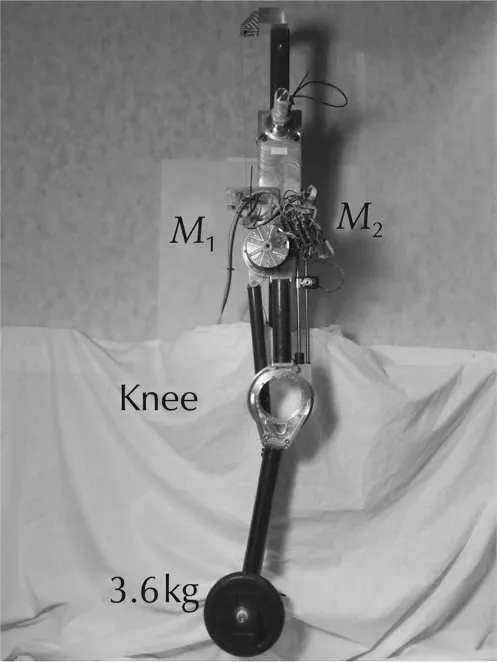
Fig.13 The prototype robotic leg used in the experiments.

4.1 Experimental prototype

A 3.6kg weight was attached at the leg end-effector(center of mass at 0.42m from the center of rotation including the mass of the lower leg)to increase the gravity load and permit a reasonable torque step magnitude.The prototype robotic leg used has two actuators(M1and M2)which both move the knee joint while the hip is un-actuated.In this experiment,the second actuator M2which applies assistive torque at the knee using a bungee cord was removed and only the main knee motor M1was used for the experimental verification.Moreover,the hip joint was mechanically locked and the leg was tested while fixed above the ground on the supporting frame.

4.2 Sensors

The torque signal is measured using two 19bit encoders measuring the deflection of a torsion bar with known stiffness(930N·m/rad),connected between the gearbox output and the link output.

The velocity is not measured and estimated using first-order differentiation of position and then a third-order Butter worth filter with cut-off frequency of 50Hz.Acceleration and jerk are obtained with first-order differentiation of the estimated velocity and acceleration,respectively.

4.3 Controller design

The PI controller Gc(s)=2(s+10)/s was designed to have 46Hz closed-loop bandwidth with full positive feedback.The closed-loop system also remains stable for the same PI controller without positive feedback compensation but the closed-loop bandwidth is substantially reduced to 0.7Hz.

The estimated value of joint damping BLis 1.5 for the leg.Note that this value of BLis much larger than the joint damping used in the simulation study presented in Section 3.The positive feedback used in the experiments are computed from the actuator and transmission parameters given in Table 2 as follows:

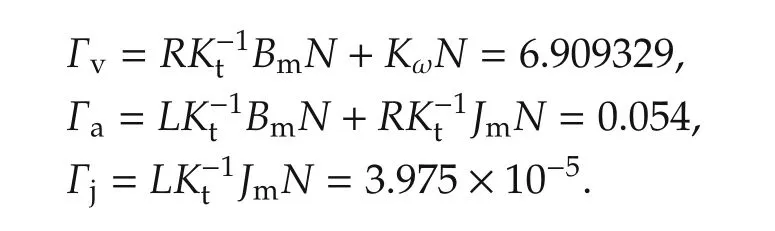
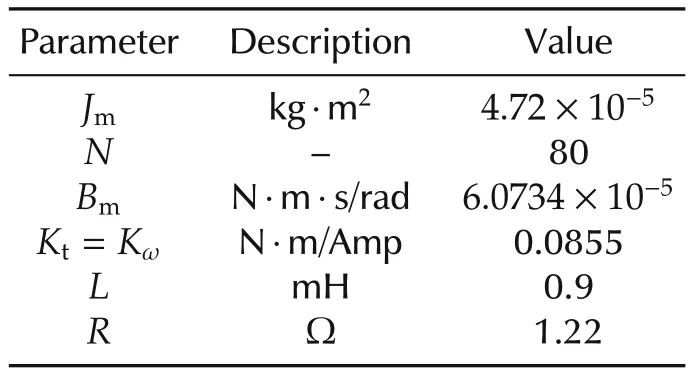
Table 2 The actuator parameter values.

4.4 Results

In the experiments a torque step of 3N·m was applied and the results are presented as follows.Fig.14 compares the system’s torque step response in four cases.The step torque reference(τr)is applied at t=0.4s.

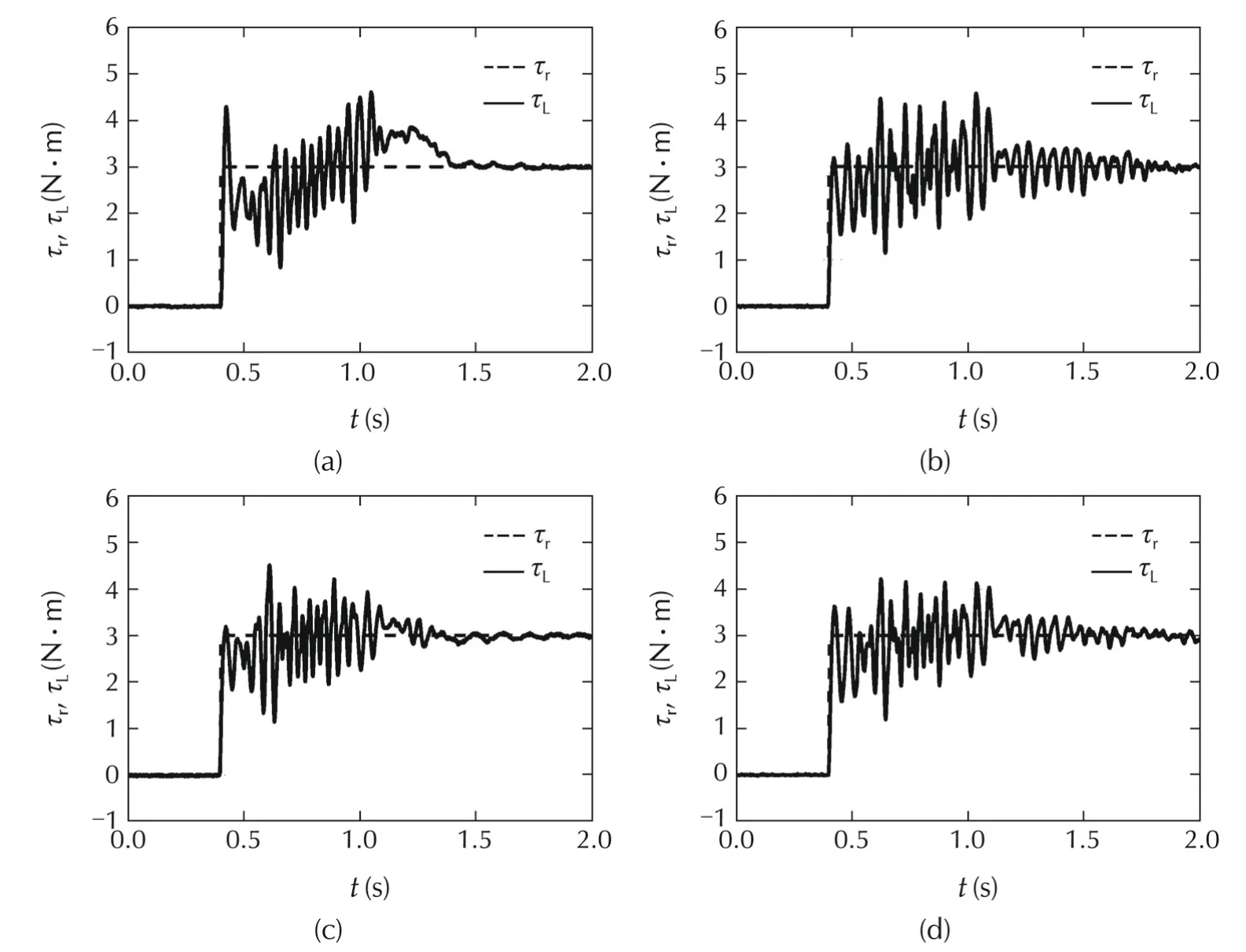
Fig.14 The experimental results of applying the positive feedback of the prototype leg.Torque reference and torque response are shown with dashed,solid lines,respectively.Parts(a)-(d)show the PI control,PI control with velocity compensation,PI control with velocity and acceleration compensation and PI control with velocity,acceleration and jerk compensation,respectively.

First,part(a)in Fig.14 shows the closed-loop step response without positive feedback.Second,in part(b)the same PI controller is used with positive velocity feedback Γv=6.909329.Third,part(c)the PI controller is used with positive velocity and acceleration feedback Γa=0.054354.Finally,in part(d)the same PI controller is used with full positive feedback proposed in Lemma 2 with positive velocity(Γv),acceleration(Γa)and jerk feedback Γj=3.975e-5.The bandwidth of the torque control system with the velocity feedback increases to 46Hz.As mentioned,since BL=1.5 is large we can ignore the acceleration and jerk feedback terms without causing instability or degrading closed-loop performance.When using the positive feedback compensation(see Fig.14)the torque settles at the desired value but a 15-20Hz ripple can be observed which is due to the harmonic drive gearbox friction.This frequency range is shown in the power spectral density graph in Fig.15.

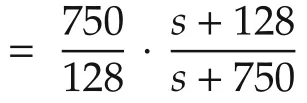
Fig.15 Spectral density plot of the uncompensated(without notch compensation)torque response.

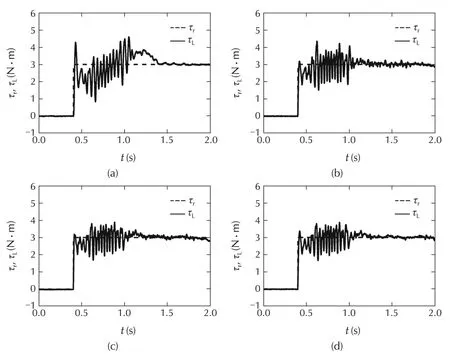
Fig.16 The experimental results of applying the positive feedback with lead compensation of the prototype leg.Torque reference and torque response are shown with dashed,solid lines,respectively.Parts(a)-(d)show the PI control,PI control with velocity and lead compensation,PI control with velocity,acceleration and lead compensation and PI control with velocity,acceleration,jerk and lead compensation,respectively.

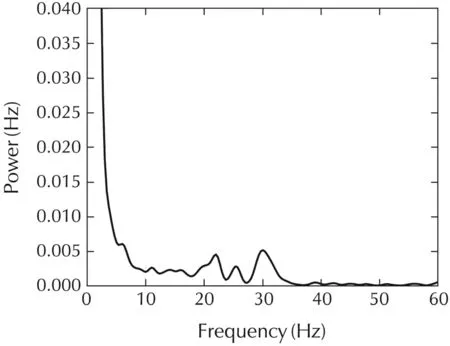
Fig.17 Spectral density plot of the lead compensated torque response.

5 Conclusions

This paper provides a detailed study regarding the use of positive feedback to improve torque control in flexible joint robots driven by electrical actuators.Itis shown that torque control bandwidth limitations depend on the load dynamics and a positive feedback scheme can be obtained to improve torque tracking for robots with electrical actuators.A two DoF nonlinear system is used as an example to illustrate torque tracking improvements that can be achieved with positive feedback and simple PI controllers.Approximate positive feedback implementations are also considered and closed-loop stability is analyzed using root locus methods.Simulations and experimental results for a prototype robot are shown to confirm the theoretical results.

[1]H.Vallery,R.Ekkelenkamp,H.Van Der Kooij,et al.Passive and accurate torque control of series elastic actuators.Proceedings of the IEEE International Conference on Intelligent Robots and Systems,San Diego:IEEE,2007:3534-3538.

[2]G.A.Pratt,M.M.Williamson.Series elastic actuators.Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems,Los Alamitos:IEEE Computer Society,1995:399-406.

[3]G.A.Pratt,M.M.Williamson.Stiffness Isn’t Everything.Proceedings of the 4th International Symposium on Experimental Robotics IV,Berlin:Springer,1995:253-262.

[4]S.J.Dyke,B.F.Spencer Jr.,P.Quast,et al.Role of control structure interaction in protective system design.ASCE Journal of Engineering Mechanics,1995,121(2):322-338.

[5]A.Alleyne,R.Liu,H.Wright.On the limitations of force tracking control for hydraulic active suspensions.Proceedings of the American Control Conference,Philadelphia:IEEE,1999:43-47.

[6] J.Dimig,C.Shield,C.French,et al.Effective force testing:A method of seismic simulation for structural testing.ASCE Journal of Structural Engineering,1999,125(9):1028-1037.

[7]C.K.Shield,C.W.French,J.Timm.Development and implementation of the effective force testing method for seismic simulation of large-scale structures.Philosophical Transactions of the Royal Society of London Series A-Mathematical Physical and Engineering Sciences,2001,359(1786):1911-1929.

[8]M.Hashimoto,Y.Kiyosawa.Experimental study on torque control using harmonic drive built-in torque sensors.Journal of Robotic Systems,1998,15(8):435-445.

[9]T.Boaventura,M.Focchi,M.Frigerio,et al.On the role of load motion compensation in high-performance force control.Proceedings of IEEE International Conference on Intelligent Robots and Systems(IROS),Algarve,Portugal:IEEE,2012:4066-4071.

[10]C.Semini,N.G.Tsagarakis,E.Guglielmino,etal.Design of HyQ-a hydraulically and electrically actuated quadruped robot.IMechE Part I:Journal of Systems and Control Engineering,2011,225(I6):831-849.

[11]F.Aghili,M.Buehler,J.M.Hollerbach.Motion control systems with H∞positive joint torque feedback.IEEE Transactions on Control Systems Technology,2001,9(5):685-695.

[12]J.S.Yeon,J.H.Park.Practical robust control for flexible joint robot manipulators.Proceedings of IEEE International Conference on Robotics and Automation,Piscataway:IEEE,2008:3377-3382.

[13]G.Hirzinger,A.Albu-Schaeffer,M.Haehnle,et al.On a new generation of torque controlled light-weight robots.Proceedings of IEEE International Conference on Robotics and Automation,New York:IEEE,2001:3356-3363.

[14]N.G.Tsagarakis,S.Morfey,H.Dallali,et al.An asymmetric compliant antagonistic joint design for high performance mobility.Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS),Tokyo:IEEE,2013:5512-5517.

[15]S.Skogestad,I.Postlethwaite.Multivariable Feedback Control:Analysis and Design.2nd ed.New York:Wiley-Blackwell,2007.

[16]B.A.Levant.Higher-order sliding modes,differentiation and output-feedback control.International Journal of Control.2003:76(9/10):924-941.

[17]C.A.Levant,M.Livne.Exact differentiation of signals with unbounded higher order derivatives.IEEE Transactions on Automatic Control,2012,57(4):1076-1080.

[18]E.S.Ibrir.Linear time-derivative trackers.Automatica,2004,40(3):397-405.

[19]M.Smaoui,X.Brun,D.Thomasset.High-order sliding mode for an electropneumatic system:A robust differentiator-controller design.International Journal of Robust and Nonlinear Control,2008,18(4/5):481-501.

[20]Y.Su,C.Zheng,D.Sun,et al.A simple nonlinear velocity estimator for high-performance motion control.IEEE Transactions on Industrial Electronics,2005,52(4):1161-1169.

[21]T.D.Tuttle,W.A.Seering.A nonlinear model of a harmonic drive gear transmission. IEEE Transactions on Robotics and Automation,1996,12(3):368-374.

[22]E.Garcia,P.G.de Santos,C.C.de Wit.Velocity dependence in the cyclic friction arising with gears.International Journal of Robotics Research,2002,21(9):761-771.

[23]P.Tomei.A Simple PD controller for robots with elastic joints.IEEE Transactions on Automatic Control,1991,36(10):1208-1213.

[24]A.De Luca,B.Siciliano,L.Zollo.PD control with on-line gravity compensation for robots with elastic joints:Theory and experiments.Automatica,2005,41(10):1809-1819.

Appendix

A1 Proof of Lemma 1

The linearized system equations can be written as W(s)×[i θmθL]T=B vmwhere

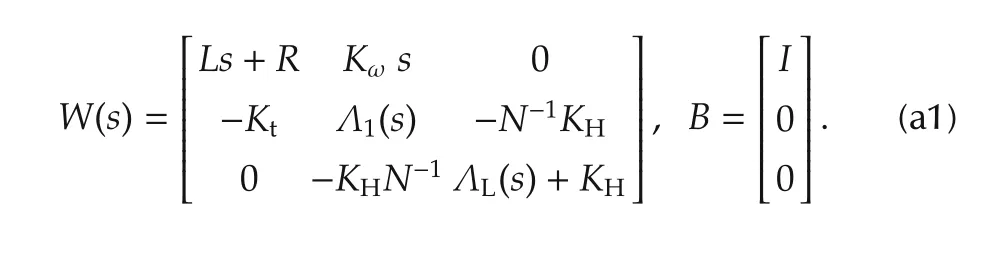
Λ1(s)= Λm(s)+N-1KHN-1,Λm(s)=+Bms,ΛL(s)=MLs2+BLs+KLand KLincludes the linearized gravity torques.The system matrix P(s)is defined as

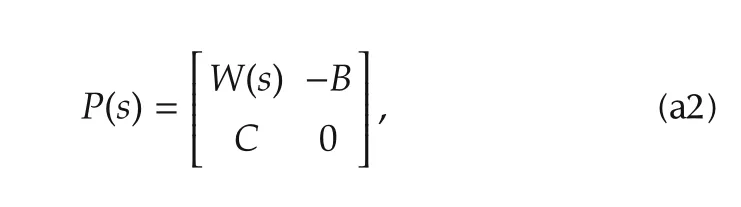
where C=[0 KHN-1-KH].The system zeros are the values s0where P(s0)looses rank,that is

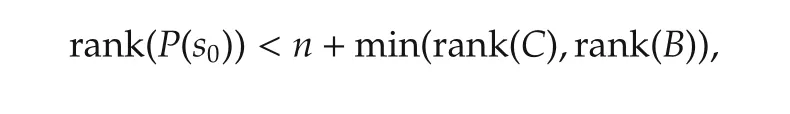
where n is twice the number of DoF.The system zeros include the transmission zeros and input/output decoupling zeros.When the system is controllable and observable there are no input/output decoupling zeros.In the transfer function matrix,input/output decoupling zeros cancel out with uncontrollable and/or unobservable poles.

We need to show that P(s)looses rank iff det(MLs2+BLs+KL)=0.To accomplish this we carry out a series of elementary transformation of the system matrix P(s).These transformations amount to post-multiply and/or pre-multiply P(s0)by a series of unimodular matrices.A unimodular matrix is a square polynomial matrix that has a constant(non-zero)determinant.The inverse of a unimodular matrix is also a unimodular matrix.

Let˜P(s)=Q1(s)P(s)Q2(s),

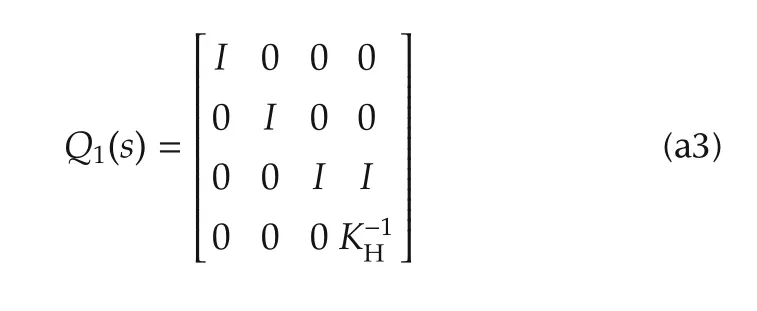
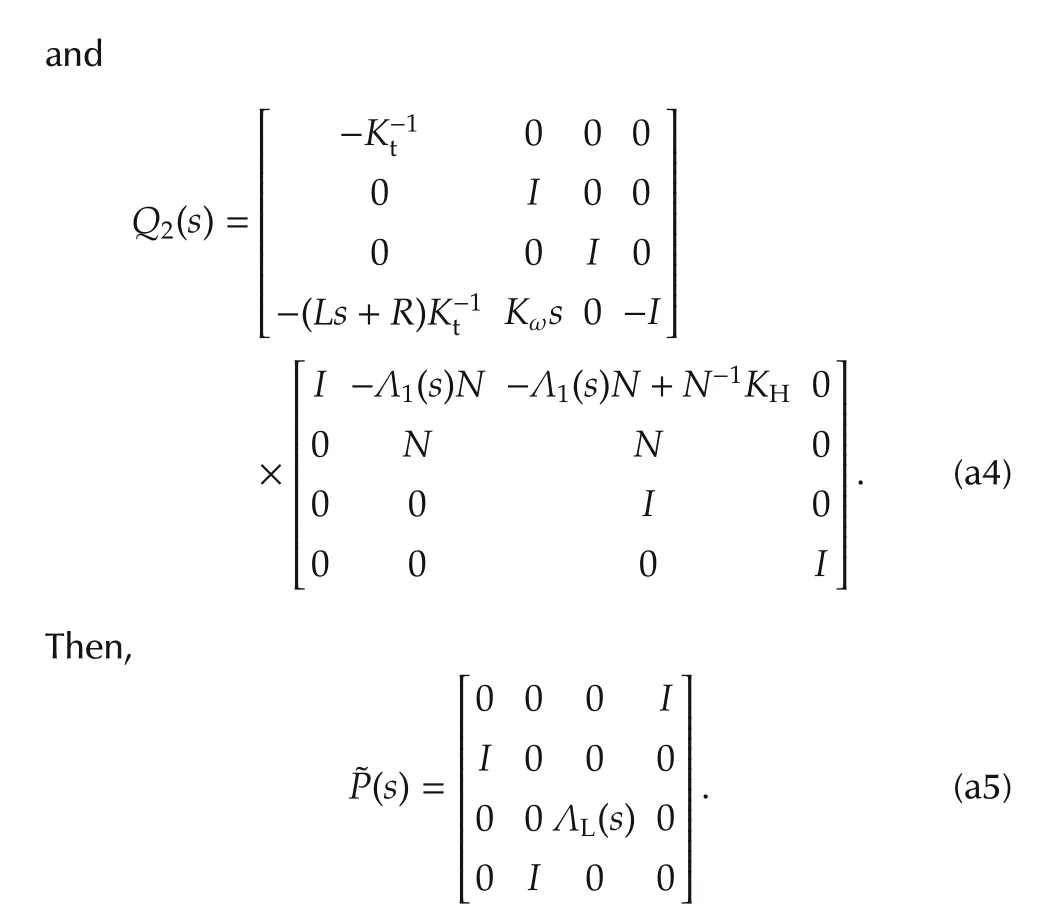
It is clear that Q1(s)and Q2(s)are unimodular matrices and therefore P(s)and˜P(s)are equivalent.It is also evident that ˜P(s)looses rank iff ΛL(s)looses rank and this in turn is equivalent to the condition det(ΛL(s))=0.

A2 Proof of Lemma 2

The plant output torque is given by

Converting(a1)in terms of torque τLgives

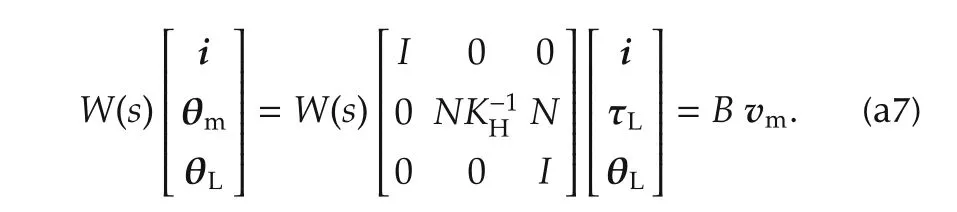
Let

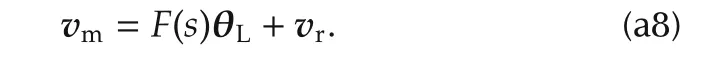
Then,(a6),(a1),(a7)and(a8)yield

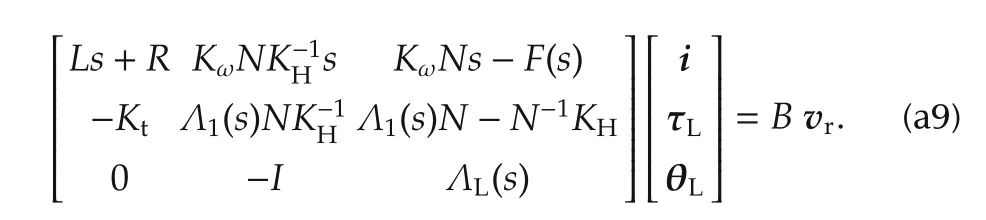
From(a9)solving for the motor current i,substituting in the equation for the torque τLand pre-multiplying by(Ls+R)K-1tyields

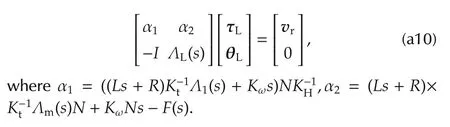
A3 Block companion matrix

Consider a polynomial matrix P(s)=P1s+P0where Piand p×p constant matrices and Pnis invertible.A block companion matrix representation of P(s)is given in(a11),where 0 and I are p×p zero and identity matrices,respectively.

28 October 2014;revised 14 May 2015;accepted 18 May 2015

†Corresponding author.

E-mail:houman.dallali@iit.it.Tel.:+39 010 71781 821;fax:+39 010 71781 232.

This work was supported by the AMARSI(Adaptive Modular Architecture for Rich Motor Skills,FP7-ICT-248311)and Walk-Man(FP7-ICT-611832)European projects.

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg

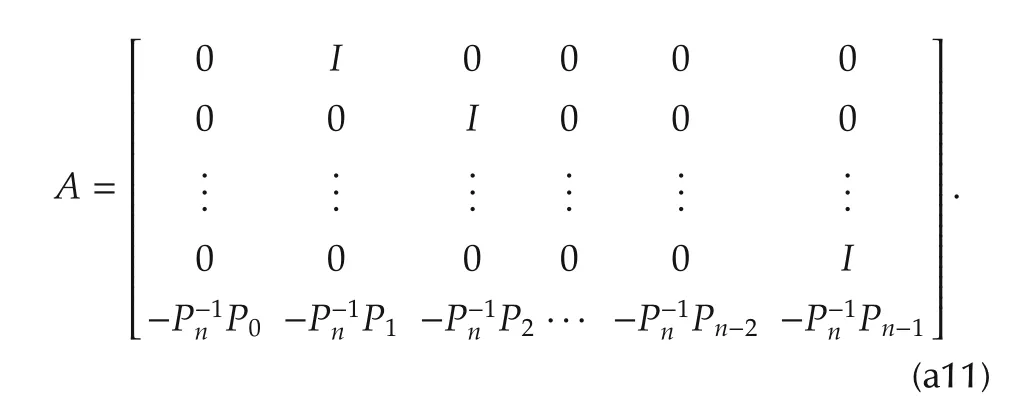
Houman DALLALI obtained the M.Sc.degree from the Department of Automatic Control and Systems Engineering at the University of Sheffield with distinction, and subsequently was admitted to the University of Manchester for pursuing his Ph.D.in modelling and stabilization control of a compliant humanoid robot,COMAN.Following the award of his Ph.D.in 2012,he was accepted for postdoctoral fellowship at the Advanced Robotics Department,the Italian Institute of Technology(IIT),Genova,Italy.In his postdoctoral fellowship in addition to work on applied control theory,he has been developing an accurate humanoid dynamic simulator for studying whole body motion and locomotion of COMAN and WALKMAN humanoid robots.His research interests are in dynamic mod-elling,multivariable impedance and force control of safe humanoid robots with flexible joints.E-mail:houman.dallali@iit.it.

Gustavo A.MEDRANO-CERDA received the B.Sc.degree in Electro-mechanical Engineering from the Universidad Nacional Autonoma de Mexico in 1977,and the M.Sc.andPh.D.degreesin Control Systems from Imperial College,London,in 1979 and 1982,respectively.From 1982 to 1985,he was an associate professor at the Division de Estudios de Postgrado, Facultad de Ingenieria,Universidad Nacional Autonoma de Mexico.From 1985 to 1986,he was a research fellow at the Department of Engineering,University of Warwick.From 1986 to 2002,he was a lecturer at the Department of Electronic and Electrical Engineering at the University of Salford.During this period,he set up the Advanced Control and Robot Locomotion Laboratory at the University of Salford.In 1999,he became a control systems consultant at Las Cumbres Observatory(formerly Telescope Technologies Ltd.)and later in 2002 he joined the company as a senior control engineer pioneering work in H-infinity control system design and implementation for astronomical telescopes.Since 2009,he has been a senior research scientist at the Advanced Robotics Department,Istituto Italiano di Tecnologia.His research interests are in the areas of robust control,adaptive control,modelling and identification,fuzzy systems and advanced robotic applications,in particular to walking robots.E-mail:gmedranocerda@googlemail.com.

Michele FOCCHI was born in Rimini,Italy.He holds the M.Sc.in Control System Engineering from Politectico di Milano in 2007.His final project dealt with dynamic modelling of hydraulic turbines for energy generation carried out at the Federal University of Santa Catarina,Brazil.Until 2008 he worked at the Ramp;D department of Indesit company where he worked with design and dynamic modeling of hydraulic,thermal and mechanical phenomena and system identification for house appliances.In 2009,he was employed as a fellow at the Advanced Robotic Department(ADVR)at IIT developing a prototype of Novel concept for an air-pressure driven micro-turbine for power generation for which he obtained an international patent and several awards.He also gained some experience with force control with pneumatic muscles.In 2010,he started a Ph.D.getting involved in the Hydraulically Actuated Quadruped Robot project at the Dynamic Legged Systems Laboratory at ADVR where he was involved on development of low-level controllers for locomotion purposes.Currently,his research interests range from dynamic locomotion with legged robots,whole body control and planning,to actuation technologies.E-mail:michele.focchi@iit.it.

Thiago BOAVENTURA received his B.Sc.andM.Sc.degreesin Mechatronic Engineering from the Federal University of Santa Catarina,Brazil,in 2009.He received his Ph.D.degree in Robotics,Cognition,and Interaction Technologies from a partnership between the Italian Institute of Technology and University of Genoa,Italy,in 2013.He is currently a post-doctoral researcher at the Agileamp;Dexterous Robotics Lab,at ETH Zurich,in Switzerland.He is mainly involved in the EU FP7 BALANCE project with focus in the collaborative impedance control of exoskeletons.His research interests include impedance and admittance control,model-based control,legged robotics,passivity of sample-based systems,hydraulic actuators and systems,variable stiffness actuators,and wearable robotics.E-mail:tboaventura@ethz.ch.

Marco FRIGERIO graduated in Computer Science in 2008,at the University of Milano Bicocca(Italy).In 2013,he obtained a Ph.D.degree in Robotics at the Advanced Robotics Department(ADVR)of Istituto Ital-iano di Tecnologia(IIT,located in Genoa,Italy).His thesis focuses on a novel approach for optimized code generation for the kinematics and the dynamics of articulated robots.Since 2013,he has been a postdoctoral researcher at the Dynamic Legged Systems Lab of ADVR at IIT.He is responsible for the software development efforts of the lab,which focus on control,legged locomotion, autonomous robots. His research interests include robotics software,software architectures and robot dynamics.E-mail:Marco.Frigerio@iit.it.

Claudio SEMINI is currently the head of IIT’s Dynamic Legged Systems Lab that developed the HyQ and HyQ2Max robot platforms,which are able to perform highly dynamic tasks such as running and jumping.After his M.Sc.at ETH Zurich,he spent 2 years in Japan for robotics research.Since the beginning of 2007,he has been a member of the Advanced Robotics Department at the Italian Institute of Technology(IIT).In spring 2007,he started the HyQ project as his Ph.D.research under the supervision of Nikos Tsagarakis and Darwin Caldwell.In 2010,he finished the design and construction of the first version of HyQ and successfully defended his Ph.D.with the title“HyQ - Design and Development of a Hydraulically Actuated Quadruped Robot”.His current research focus lies on the design and control of hydraulically actuated high-performance robots with arms and legs,compact hydraulic actuation and hydraulic force control.E-mail:Claudio.Semini@iit.it.

Jonas BUCHLI is an SNSF Assistant Professor for Agile and Dexterous Robotics at ETH Zurich since May 2012.He holds a Diploma in Electrical Engineering from ETH Zurich(2003)and a Ph.D.from EPF Lausanne(2007).He has contributed to research in diverse fields such dynamical systems approaches to motion generation and control,the theory of coupled oscillators,planning and control of dynamic locomotion,machine learning,whole body control,whole body force and impedance control and modeling of human motor control.He was involved in the development of robotic platforms as well as software engineering projects for robotic control software.His current research interests include model based control of legged robotic and human locomotion and manipulation,optimal and learning control,and dynamic and versatile service and field robots.E-mail:buchlij@ethz.ch.

Darwin G.CALDWELL(born in Ballymena,Northern Ireland)is a noted international researcher and academic in Robotics who is currently Research Director at the Italian Institute of Technology in Genoa,Italy.He has been heavily involved as project leader in the development of the iCub,a smallsize humanoid robot being designed by the RobotCub Consortium.He has published over 170 papers and has received awards at several international conference and events.He is a visiting professor at the University of Sheffield,King’s College London,University of Wales Bangor and University of Manchester.He studied at Ballymena Academy and then completed his B.Sc.and Ph.D.in Robotics from the University of Hull in 1986 and 1990,respectively,and completed an M.Sc.in Management at the University of Salford in 1994.His research interests include innovative actuators and sensors,haptic feedback,force augmentation exoskeletons,dexterous manipulators,humanoid robotics(iCub),bipedal and quadrupedal robots,biomimetic systems,rehabilitation robotics,telepresence and teleoperation procedures,and robotics and automation systems for the food industry.He was previously at the University of Salford between 1989 to 2007 as a Lecturer,Senior Lecturer,Reader and finally Professor of Advanced Robotics in the Centre for Robotics and Automation between 1999 and 2007.He is currently Chair of the IEEE Robotics and Automation Chapter(UKRI)and a past co-chair of the IEE(IET)Robotics and Mechatronics.He is on the editorial board of Industrial Robot as well as being guest editor of several journals.In association with Professor John Gray of the University of Salford,he was responsible for the establishment of the Yorkshire Forward funded Centre for Food Robotics and Automation(CenFRA).E-mail:darwin.caldwell@iit.it.