Infinite horizon indefinite stochastic linear quadratic control for discrete-time systems

Weihai ZHANG,Yan LI,Xikui LIU

1.College of Electrical Engineering and Automation,Shandong University of Science and Technology,Qingdao Shandong 266590,China;

2.College of Mathematics and Systems Science,Shandong University of Science and Technology,Qingdao Shandong 266590,China

Infinite horizon indefinite stochastic linear quadratic control for discrete-time systems

Weihai ZHANG1†,Yan LI1,Xikui LIU2

1.College of Electrical Engineering and Automation,Shandong University of Science and Technology,Qingdao Shandong 266590,China;

2.College of Mathematics and Systems Science,Shandong University of Science and Technology,Qingdao Shandong 266590,China

This paper discusses discrete-time stochastic linear quadratic(LQ)problem in the infinite horizon with state and control dependent noise,where the weighting matrices in the cost function are assumed to be indefinite.The problem gives rise to a generalized algebraic Riccati equation(GARE)that involves equality and inequality constraints. The well-posedness of the indefinite LQ problem is shown to be equivalent to the feasibility of a linear matrix inequality(LMI).Moreover,the existence of a stabilizing solution to the GARE is equivalent to the attainability of the LQ problem.All the optimal controls are obtained in terms of the solution to the GARE.Finally,we give an LMI-based approach to solve the GARE via a semidefinite programming.

Indefinite stochastic LQ control,discrete-time stochastic systems,generalized algebraic Riccati equation,linear matrix inequality,semidefinite programming

DOI10.1007/s11768-015-4147-x

1 Introduction

It is well known that the linear quadratic(LQ)optimal control problem of deterministic systems was first founded by Kalman[1],which has been playing important role in both theory and applications.The deterministic LQ problem has been discussed extensively by many researchers;see,e.g.,[2-5].The stochastic LQ problem was initiated by Wonham[6]and has been investigated;see[7-14]and the references therein.In the literature,it is a common assumption that the control weighting matrix should be positive definite and the state weighting matrix should be nonnegative.In this case,the solvability of the LQ problem is equivalent to that of the Riccati equations.However,a class of stochastic LQ problems with indefinite control weightsmay still be well-posed[15].The solvability of indefinite stochastic LQ problem is closely linked to the solvability of the indefinite stochastic Riccati equations.There are many works focusing on this issue,we refer the reader to[16-18].

For the discrete-time LQ control,Y.Huang et al.[19,20]studied a class of special cases,where the system is described by a difference equation with control and state dependent noise.In[21],the optimal control is obtained for the systems with only control dependent noise.These papers dealt with the LQ problem with the positive definite control weighting matrices in the cost functional.A discrete-time indefinite LQ control in a finite horizon with state and control dependent noise is studied in[22].Analytical properties of the constrained discrete-time indefinite stochastic LQ control in finite time horizon were extensively studied in[23-25].

This paper considers the discrete-time indefinite stochastic LQ problem in the infinite horizon.Different from the finite horizon case,in order to guarantee the well-posedness of the LQ problem and the existence of the feedback stabilizing control,we have to define some concepts such as stabilizability.A generalized algebraic Riccati equation(GARE)is introduced.It turns out that the attainability of the LQ problem is necessary and sufficient for the existence of the stabilizing solution to the GARE.Meanwhile,we introduce a linear matrix inequality(LMI)condition and show that the well-posedness of the LQ problem is equivalent to the feasibility of the LMI.Furthermore,we present all optimal controls via the solution to the GARE.Finally,we give an LMI-based approach to solve the GARE via a semidefinite programming.

The remainder of this paper is organized as follows.In Section2,we present the notions of stabilizability and some preliminaries.Section3 shows that the solvability of the GARE is sufficient for the well-posedness of theLQ problem and the existence of an optimal control.Section4 contains main results of the paper.In Section5,we give an LMI-based approach to solve the GARE via a semidefinite programming.Section6 ends this paper with some concluding remarks.

For convenience,we adopt the following notations.M?represents the transpose of a matrix M;Tr(M)is the trace of asquare matrixM;M＞0(M≥0)means that Mis a positive definite(positive semi-definite)symmetric matrix;E[x]represents the mathematical expectation of a random variable x;Rkis the k-dimensional Euclidean space with the usual 2-norm ‖·‖;Rm×nis the vector space of all m×n matrices with entries in R;M†means the Moore-Penrose pseudo inverse of a matrix M;I is the identity matrix with an appropriate dimension;Sndenotes the set of all real n×n symmetric matrices;and N={0,1,2,...}.

2 Problem formulation and preliminaries

Consider the following stochastic discrete-time system of the form:

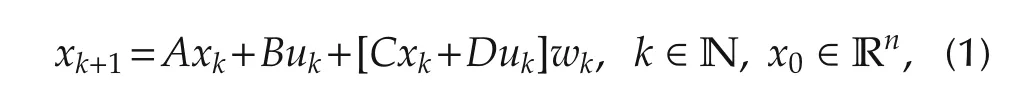
where A,B,C and D are constant matrices with appropriate dimensions.x∈Rnis called the system state,u∈Rmis the control input.x0∈Rnis the initial state which is deterministic.{wk}k≥0are the one-dimensional independent random variables defined on the complete probability space(Ω,F,P),such that E[wk]=0 and E[wswt]= δst,where δstis the Kronecker delta.

We denote Fkthe σ-algebra generated by wk,k ∈ N,i.e.,Fk= σ(ws:1 ≤ s≤ k).Let L2(Ω,Rm)represent the space of Rm-valued random vectors ξ with E‖ξ‖2＜ ∞.(N,Rm)consists of all sequences y={yk:yk∈ Rm}k∈N,such that yk∈ L2(Ω,Rm)is Fk-1measurable for k ∈ N,where we define F-1={φ,Ω},i.e.,y0is a constant.The l2-norm of yis defined by

For simplicity of our discussion,we give the following definitions.

De fi nition 1 Consider system(1)with uk=0.System(1)is said to be mean-square stable[19]if for any x0∈Rn,the corresponding state satisfies0.u={uk:k∈N}(may be an open-loop control)is said to be a mean-square stabilizing control(with respect to x0)if the corresponding state xkof(1)satisfies=0.u={uk:k ∈ N}with uk=Kxkis called a mean-square feedback stabilizing control law if for every x0,the closed-loop system

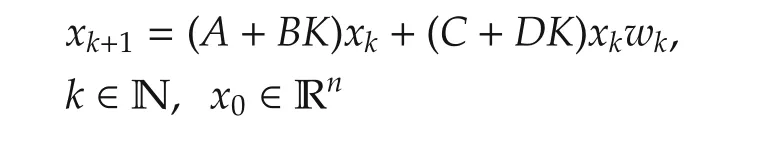
is mean-square stable,where K is a constant matrix.

Definition 2 System(1)is said to be stabilizable in the mean square sense if there exists a mean-square feedback stabilizing control law uk=Kxk,where K is a constant matrix.

For system(1),the admissible control set Uad(x0)is defined as follows:

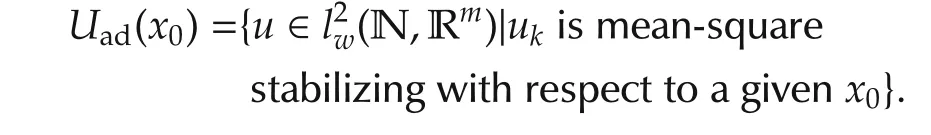
For any(x0,uk)∈Rn×Uad(x0),the associated cost functional to system(1)is defined as

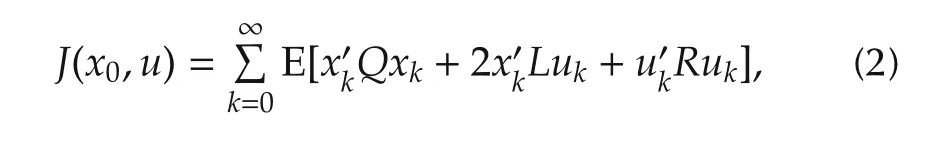
whereL∈Rn×m,Q ∈SnandR∈Smaregivenmatrices.

The LQ optimal control problem is to find a control sequence u∗=(u∗0,...,u∗n,...)∈ Uad(x0)such that

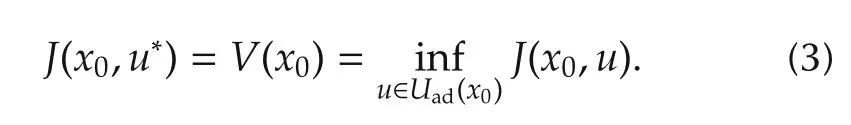
We call V(x0)the optimal cost value.

Definition 3 The LQ problem is called well-posed if

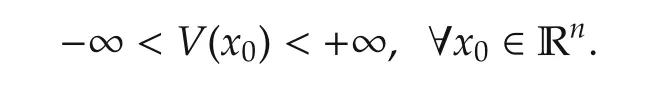
A well-posed LQ problem is called attainable if there exists a control sequence(u∗0,...,u∗n...)that achieves V(x0).

We suppose that system(1)is stabilizable throughout this paper.Hence,Uad(x0)is nonempty for each x0.

Now,we present a new GARE as follows.

Definition 4 The constrained algebraic equation on P∈Sn

is called a constrained GARE.

Let us give some lemmas needed in the proof of our main results.

Lemma 1[26] For any matrix M ∈ Rm×n,there is a unique matrix M†∈ Rn×m,which satisfies

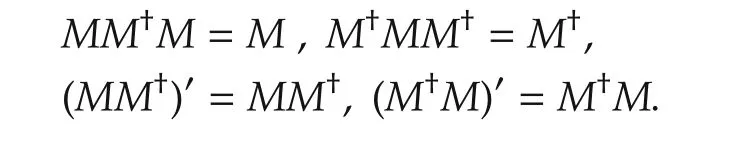
M†is called the Moore-Penrose pseudo inverse of M.

Lemma 2[26]Let a symmetric matrix M be given.Then

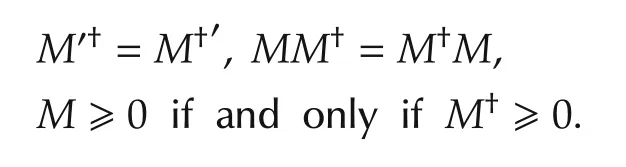
Lemma 3[22]Let matrices L,M,N be given,then the matrix equation LXM=N has a solution X if and only if LL†NMM†=N.X is given by X=L†NM†+Y-L†LYMM†,where Y is a matrix with an appropriate dimension.

Lemma 4(Extended Schur’s lemma)[27]Let matrices M=M?,N,R=R?be given with appropriate sizes.Then the following conditions are equivalent:

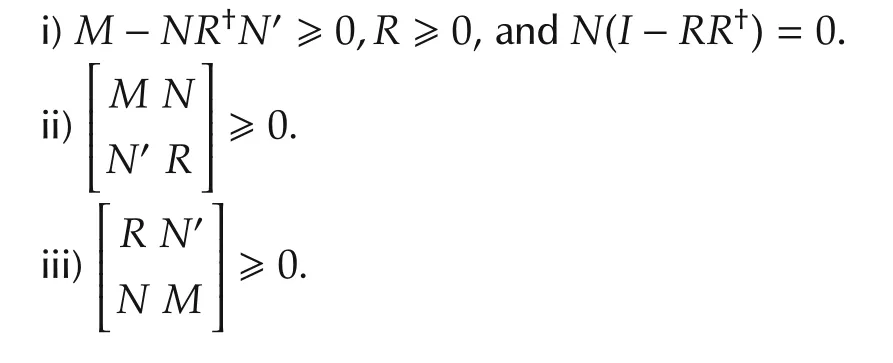
3 Sufficiency of the GARE

In this section,it is shown that the solvability of the GARE(4)is sufficient for the well-posedness of the LQ problem and the existence of an optimal control.Moreover,we show that any optimal control can be determined by means of the solution to the GARE.

Theorem 1 If the GARE(4)admits a solution P and there exist Yk∈ Rm×nand Zk∈ Rmsuch that the following control:

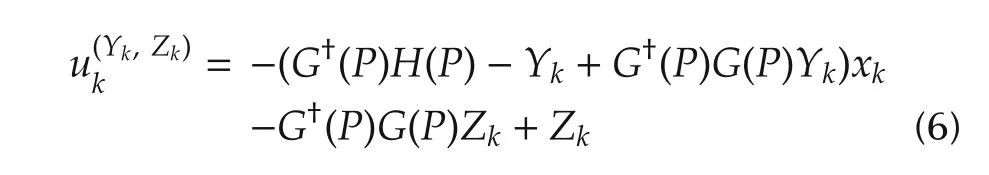
is admissible for any initial x0.Then LQ problem(1)-(3)is attainable.Furthermore,u(Yk,Zk)kis the optimal control and the optimal cost value is uniquely determined by

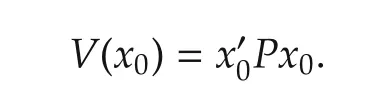
Proof Let P solve the GARE(4).It is clear that∀T∈N,P∈Sn,

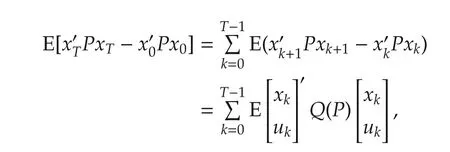
where

By adding the above equality to the performance index,we have

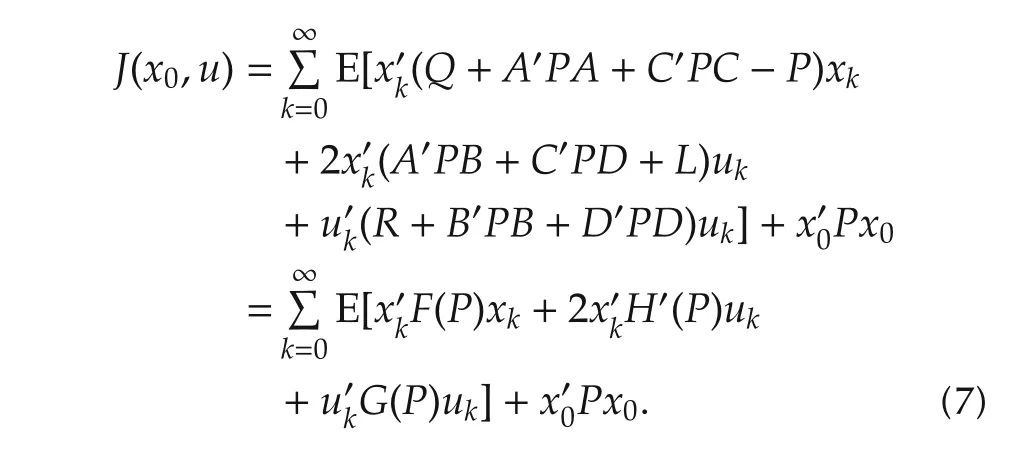
Define

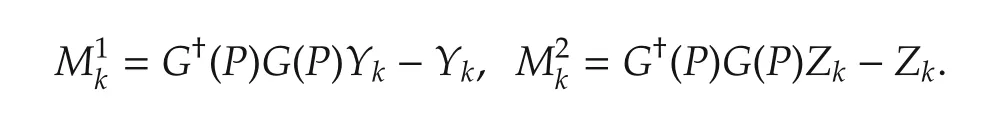
Hence,we can obtain that

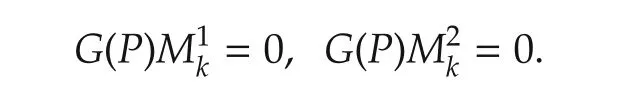
By completing squares,(7)can be rewritten as

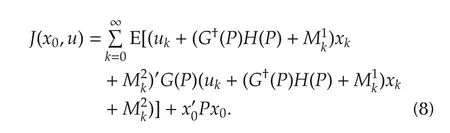
This implies that the control sequence

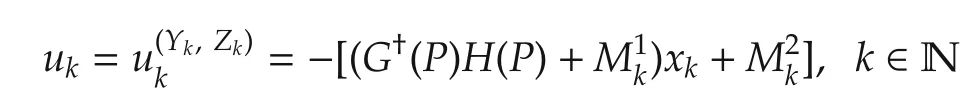
minimizes J with the optimal value given by x?0Px0. □

Definition 5 A solution P to the GARE(4)is called stabilizing if there exists an admissible control determined by(6).

Remark 1 A solution P to the GARE(4)is stabilizing if and only if for any x0there exists some Zk∈Rmsuch that the following control:is admissible,where xkis the solution to(1)under the above control with the initial state x0.

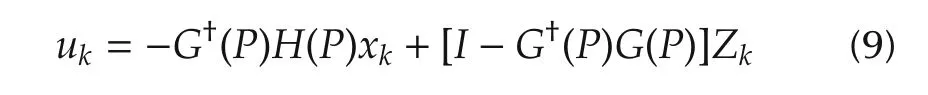
The following definition is concerned with the maximal solution.

Definition 6 A matrix P is called a maximal solution to the GARE(4)if P ≥ P∗for any P∗satisfying

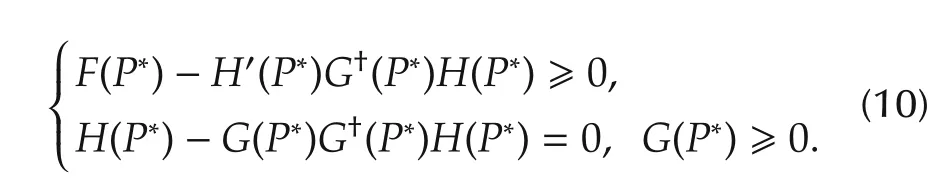
By Definition 6,it is clear that the maximal solution must be unique if it exists.Now,let us turn to the GARE(4).

Theorem 2 There is at most one stabilizing solution to(4).Moreover,a stabilizing solution to(4)is also its maximal solution.

Proof Assume that P1and P2are different stabilizing solutions to(4).By Theorem 1,it follows thatfor any x0,so P1=P2.

Let any P∗satisfy(10)and P be the stabilizing solution to(4).Putting P∗in(8)we assert that

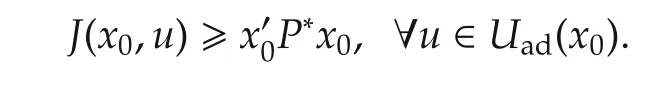
By Theorem 1,it is easy to show thatPx0=V(x0)≥x?0P∗x0.Therefore,P is a maximal stabilizing solution to the GARE due to Definition 6. □

The following corollaries are special cases of the above result.

Corollary 1 Suppose that the GARE(4)admits a stabilizing solution P.If G(P)=0,then any admissible control is optimal and the GARE(4)reduces to

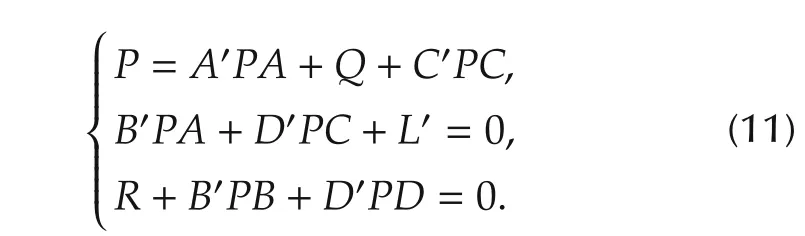
ProofBy(7)and G(P)=0,we can show that

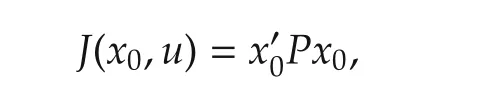
which implies that V(x0)= x?0Px0for any uk∈Uad(x0). □

Corollary 2 Let P be a stabilizing solution to the GARE(4).If G(P)＞0,then the LQ problem(1)-(3)is uniquely solvable.The unique optimal control is given by

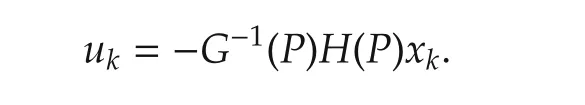
Proof Using Theorem 1,we immediately obtain Corollary 2. □

4 Well-posedness and attainability of LQ problem

In this section,we first present the connection between the well-posedness of the LQ problem and the solvability of the GARE.Then,we study the wellposedness via the LMI condition.Finally,we establish the link between the attainability of the LQ problem and the solvability of the GARE.

Lemma 5 The LQ problem(1)-(3)is well-posed if and only if there exists a symmetric constant matrix P such that

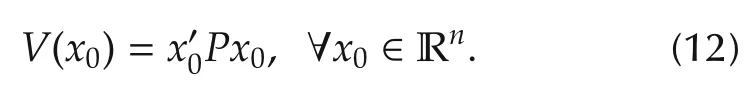
Proof (12)can be shown by a simple adaptation of the well-known result in the deterministic case[2].We introduce the following convex set P of Sn:

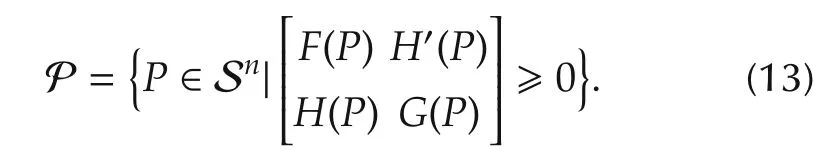
Theorem 3 The LQ problem(1)-(3)is well-posed if and only if the set P is nonempty.Moreover,there exists P∈P such that P≥˜P,∀˜P∈P.

Proof(Sufficiency) Assume that the set P is nonempty,let∀˜P∈P.Then,adding the fol lowing equality:

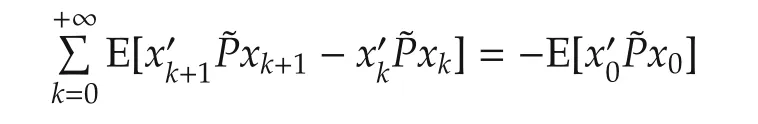
to the cost function

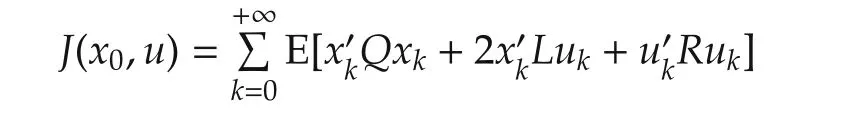
and applying(1),we can see that for any(x0,uk)∈Rn×Uad(x0),

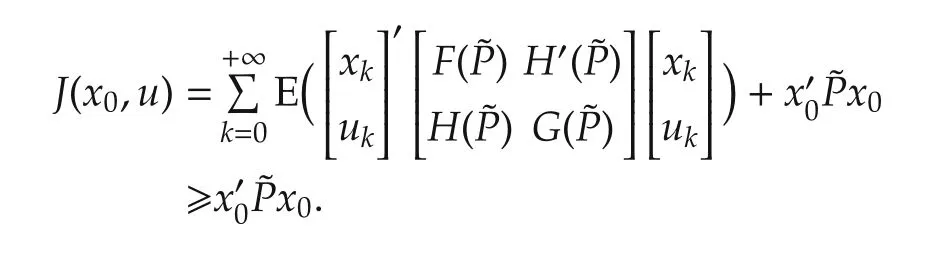
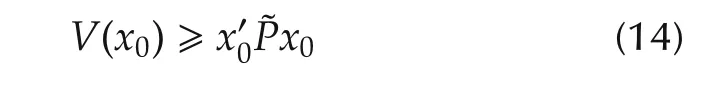
Since x0and ukare arbitrary,thus implies the well-posedness of the LQ problem.

(Necessity) Assume that the LQ problem(1)-(3)is well-posed,Lemma 5 yields that there exists a symmetric matrix P such that V(x0)=x?0Px0,∀x0∈Rn.

By the dynamic programming principle,we obtain

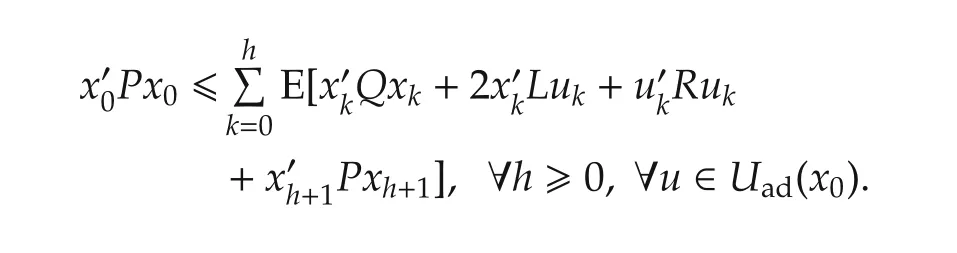
Based on(1)and the above inequality,we conclude that

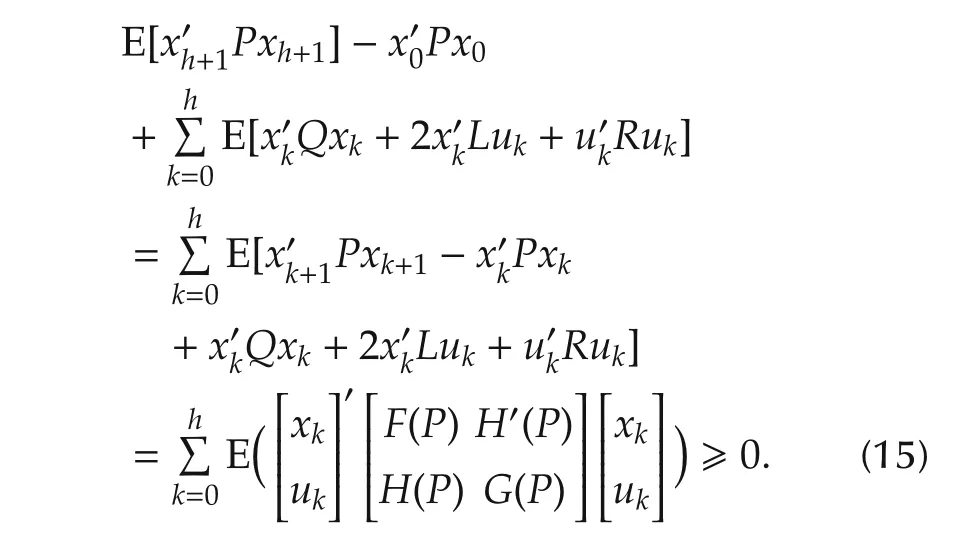
Setting uk=¯u and letting h=0,we have

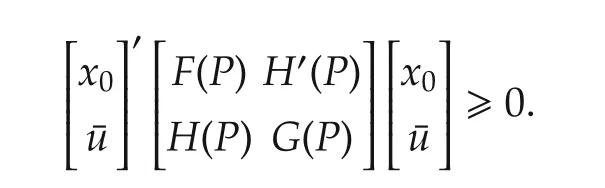
Because x0and¯u are arbitrary,it is easy to see that

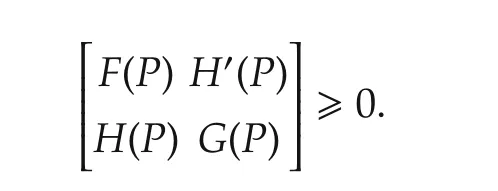
This means that P∈P.Employing(14),it follows that

The following theorem can be viewed as the converse of Theorem 1, which plays an essential role in this paper.

Theorem 4 The LQ problem(1)-(3)is attainable for any x0,then the GARE(4)has a stabilizing solution.Moreover,any optimal control is given by(6).

Proof If the LQ problem(1)-(3)is attainable,it is also well-posed.By Theorem 5,there exists a maximal element P∈P satisfying V(x0)=x?0Px0and

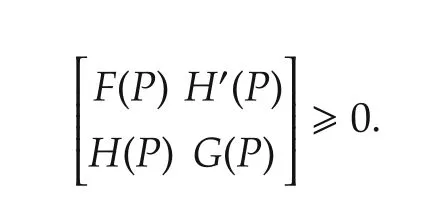
Using Lemma 4,it is obvious that

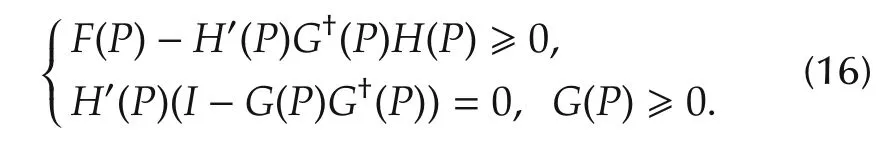
Let u∗be an optimal control for any initial x0.As same as Theorem 5,the following(17)is derived:

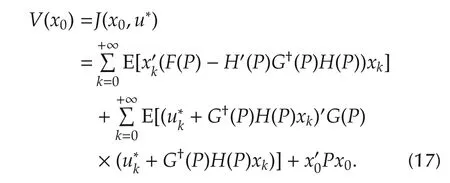
Combining(16)with V(x0)=x?0Px0,it can be shown that

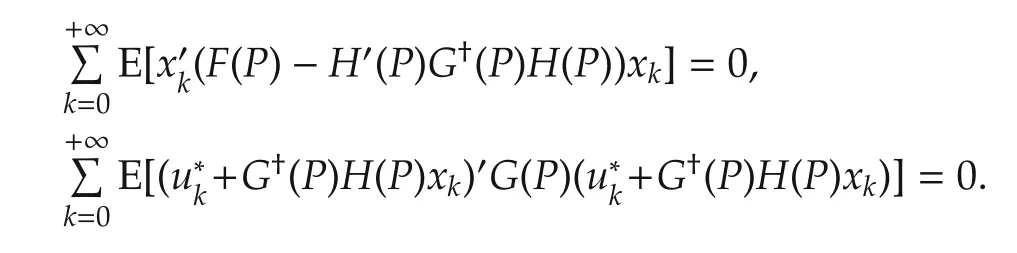
Hence,we have

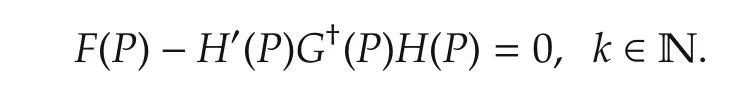
Together with(15),we obtain that P is a solution to the GARE(4).

In what follows,we show that any optimal controlcan be given by(6).From(16),it yields that

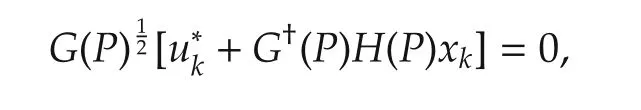
which implies

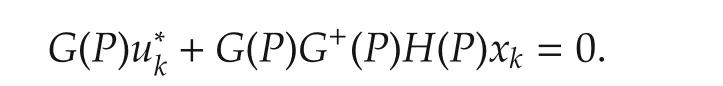
By Lemma 3 with

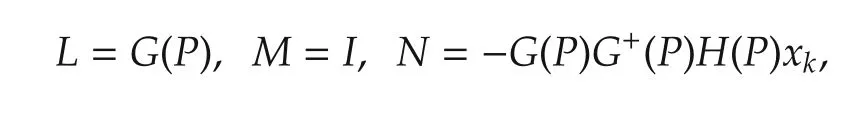
we solve the above equation and have the following solution=-G+(P)H(P)xk+Y-G+(P)G(P)Y.Thuscan be represented by(6)with Zk=Y and Yk=0.On the other hand,from Definition 5,it follows that P is a stabilizing solution to the GARE(4).

5 Characterizing LQ problem via SDP

In this section,we develop an approach based on semidefinite programming(SDP).We show that the stabilizing of the feedback control can be examined via solving a SDP problem.We establish several relations among the GARE,the SDP and the optimality of the LQ problem.

First,we introduce the following definition.

Definition 7[28] Let a vector c=(c1,...,cm)?∈Rmand matrices F0,F1,...,Fm∈Snbe given.The following optimization problem:

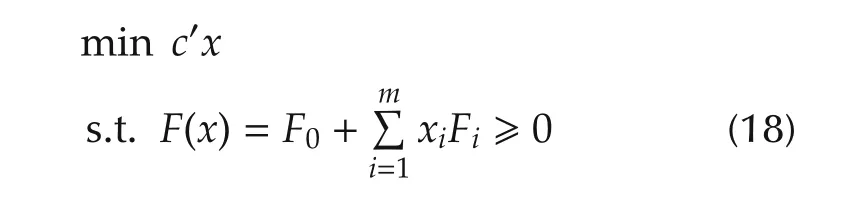
is called a semidefinite programming(SDP).The SDP is feasible if there exists an x such that F(x)≥0.

Consider the following SDP problem:

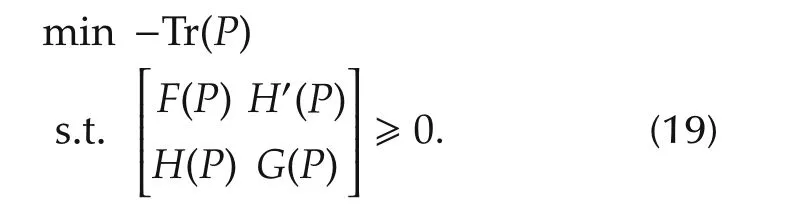
The following assertions provide connections among the well-posedness of the LQ problem,the feasibility of the SDP and the solvability of the GARE.

Theorem 5 The SDP(19)is feasible if and only if the LQ problem(1)-(3)is well-posed.

Proof By Theorem 5,we easily get the desired result.

Theorem 6 If the SDP(19)is feasible,then it has a unique optimal solution P∗satisfying V(x0)=x?0P∗x0,∀x0∈ Rn.

By Theorem 5, it follows that the SDP(19)has a maximal solution P such that V(x0)=x?0Px0,∀x0∈ Rn,which is also an optimal solution to(19).Let P∗be arbitrary optimal solution to(19).It is evident that Tr(P-P∗)=0.Moreover,the maximality of P results in P-P∗≥ 0.Therefore,P-P∗=0,i.e.,P=P∗.

Theorem 7 If the LQ problem(1)-(3)is attainable,then the unique optimal solution to(19)is the stabilizing solution to the GARE(4).

Proof From Theorems 2 and 6,the assertion is immediately obtained.

Similar to the discussion in[29],we give a computational approach to determine the lower bound of the control weighting matrix R for the LQ problem to be well-posed.

Definition 8 Let Q and L be given.The smallest r∗∈ R is called the well-posed margin if the LQ problem(1)-(3)is well-posed for any R ≥ r∗I.

Remark 2 By the above definition,if the smallest eigenvalue λmin(R)of R satisfies λmin(R) ≥ r∗,then the LQ problem is well-posed.Otherwise,the LQ problem is ill-posed.In particular,if r∗=0,the LQ problem is ill-posed for any indefinite R.

The following result shows that the well-posedness margin r∗can be obtained numerically.

Theorem 8 The well-posedness margin r∗can be derived by solving the following SDP problem:

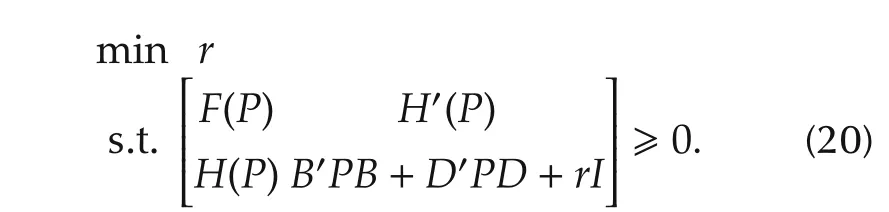
Proof From Theorem 7,Theorem 8 is easily proved. □

Example1 System(1)-(3)is specified by the follo wing matrices:

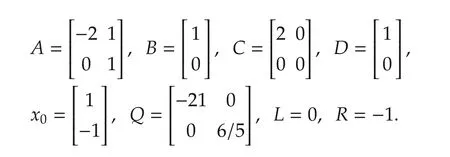
Solving the corresponding GARE(4)yields G=5,H=[0 1],P=Finally,we can calculate the optimal control sequence uk=-[0 1/5]xkand the optimal cost value V(x0)=x?0Px0=8.By Theorem 8,the well-posedness margin r∗=6.

Remark 3 In stochastic systems,there is no similar definition to transfer function as in linear system theory.Therefore,we cannot define an optimal feedback control to be proper or improper as in[30].In this paper,the admissible control set Uad(x0)is not limited to a static state feedback form,which may include other forms such as open-loop controls.However,from Theorem 4,if the LQ problem is attainable,all optimal controls take the form of(6),which completely characterizes all the optimal control forms.

6 Conclusions

This paper has investigated the infinite horizon indefinite LQ control for discrete-time stochastic systems with state and control dependent noise.A GARE has been introduced.The well-posedness of the LQ problem is equivalent to the feasibility of an LMI.Moreover,the attainability of the LQ problem is equivalent to the existence of a stabilizing solution to the GARE.All the optimal controls are obtained in terms of the solution to the GARE.To some extent,the results of this paper may be viewed as a discrete-time version of[29].

[1] R.E.Kalman.Contributions to the theory of optimal control.Boletin de la Sociedad Matematica Mexicana,1960,5:102-119.

[2]B.D.O.Anderson,J.B.Moore.Optimal Control-Linear Quadratic Methods.New York:Prentice-Hall,1989.

[3]F.L.Lewis.OptimalControl.NewYork:John Wileyamp;Sons,1986.

[4] L.Ntogramatzidis,A.Ferrante.On the solution of the Riccati differential equation arising from the LQ optimal control problem.Systemsamp;Control Letters,2010,59(2):114-121.

[5]A.Ferrante,L.Ntogrammatzidis.The generalized continuous algebraic Riccati equation and impulse-free continuous-time LQ optimal control.Automatica,2014,50(4):1176-1180.

[6]W.M.Wonham.On a matrix Riccati equation of stochastic control.SIAM Journal on Control,1968,6:312-326.

[7]D.H.Jacobson,D.H.Martin,M.Pachter,et al.Extensions of Linear-Quadratic Control Theory.Lecture Notes in Control and Information Sciences.Berlin:Springer,1980.

[8] A.Bensoussan.Stochastic Control of Partially Observed Systems.Cambridge,U.K.:Cambridge University Press,1992.

[9]M.H.A.Davis.Linear Estimation and Stochastic Control.London:Chapman and Hall,1977.

[10]E.Yaz.Infinite horizon quadratic optimal control of a class of nonlinear stochastic systems.IEEE Transactions on Automatic Control,1989,34(11):1176-1180.

[11]W.Zhang,B.Chen.On stabilizability and exact observability of stochastic systems with their applications.Automatica,2004,40(1):87-94.

[12]W.Zhang,H.Zhang,B.Chen.Generalized Lyapunov equation approach to state-dependent stochastic stabilization/detectability criterion.IEEE Transactions on Automatic Control,2008,53(7):1630-1642.

[13]Y.Hu,H.Jin,X.Zhou.Time-inconsistent stochastic linearquadratic control.SIAM Journal on Control and Optimization,2012,50(3):1548-1572.

[14]J.M.Yong.Linear-quadratic optimal control problems for mean field stochastic differential equations.SIAM Journal on Control and Optimization,2013,51(4):2809-2838.

[15]S.Chen,X.Li,X.Zhou.Stochastic linear quadratic regulators with indefinite control weight costs.SIAM Journal on Control and Optimization,1998,36(5):1685-1702.

[16]Z.Qian,X.Zhou.Existence of solutions to a class of indefinite stochastic Riccati equations.SIAM Journal on Control and Optimization,2013,51(1):221-229.

[17]Q.Meng.Linear quadratic optimal stochastic control problem driven by a Brownian motion and a Poisson random martingale measure with random cofficients.Stochastic Analysis and Applications,2014,32(1):88-109.

[18]R.S.Burachik,C.Y.Kaya,S.N.Majeed.A duality approach for solving control-constrained linear-quadratic optimal control problems.SIAM Journal on Control and Optimization,2014,52(3):1423-1456.

[19]Y.Huang,W.Zhang,H.Zhang.Infinite horizon linear quadratic optimal control for discrete-time stochastic systems.Asian Journal of Control,2008,10(5):608-615.

[20]R.T.Ku,M.Athans.Further results on the uncertainty threshold principle.IEEE Transactions on Automatic Control,1977,22(5):866-868.

[21]A.Beghi,D.D.Alessandro.Discrete-time optimal control with control-dependent noise and generalized Riccati difference equations.Auto matica,1998,34(8):1031-1034.

[22]M.Ait Rami,X.Chen,X.Zhou.Discrete-time indefinite LQ control with state and control dependent noises. Journal of Global Optimization,2002,23(3/4):245-265.

[23]G.Li,W.Zhang.Study on indefinite stochastic linear quadratic optimal control with inequality constraint.Journal of Applied Mathematics,2013:DOI 10.1155/2013/805829.

[24]W.Zhang,G.Li.Discrete-time indefinite stochastic linear quadratic optimal control with second moment constraints.Math matical Problems in Engineering,2014:DOI 10.1155/2014/278142.

[25]X.Liu,Y.Li,W.Zhang.Stochastic linear quadratic optimal control with constraint for discrete-time systems.Applied Mathematics and Computation,2014,228:264-270.

[26]R.Penrose.A generalized inverse for matrices.Mathematical Proceedings of the Cambridge Philosophical Society,1955,51(3):406-413.

[27]A.Albert.Conditions for positive and nonnegative definiteness in terms of pseudo-inverse.SIAM Journal on Applied Mathematics,1969,17(2):434-440.

[28]L.Vandenberghe,S.Boyd.Semidefinite programming.SIAM Review,1996,38(1):49-95.

[29]M.Ait Rami,X.Zhou,J.B.Moore.Well-posedness and attainability of indefinite stochastic linear quadratic control in infinite time horizon.Systemsamp;Control Letters,2000,41(2):123-133.

[30]B.R.Copeland,M.G.Safonov.Zero cancelling compensation for singular control problems and their application to the innerouter factorization problem.International Journal of Robust and Nonlinear Control,1992,2(2):139-164.

18 October 2014;revised 10 July 2015;accepted 13 July 2015

†Corresponding author.

E-mail:w_hzhang@163.com.

This work was supported by the National Natural Science Foundation of China(Nos.61174078,61170054,61402265)and the Research Fund for the Taishan Scholar Project of Shandong Province of China.

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg

Weihai ZHANG received his Ph.D.degree from Zhejiang University in 1998,Hangzhou,China.He is currently a professor of Shandong University of Science and Technology.His research interests include stochastic optimal control,robust H∞control,stochastic stability and stabilization.E-mail:w_hzhang@163.com.

Yan LI received the M.Sc.and Ph.D.degrees from Shandong University of Science and Technology,China,in 2006 and 2015,respectively.She is a lecturer of Shandong University of Science and Technology.Her research interests include linear and nonlinear stochastic control.E-mail:liyanhd@163.com.

XikuiLIU received the M.Sc.degree from Shandong University of Science and Technology,and the Ph.D.degree from Huazhong University of Science and Technology,China,in 2000 and 2004,respectively.He is a associate professor of Shandong University of Science and Technology.His interests include graph theory and DNA computing.E-mail:liuxikuiqd@163.com.