L1adaptive control with sliding-mode based adaptive law

Jie LUO,Chengyu CAO

Department of Mechanical Engineering,University of Connecticut,Storrs,CT 06269,U.S.A.

L1adaptive control with sliding-mode based adaptive law

Jie LUO†,Chengyu CAO

Department of Mechanical Engineering,University of Connecticut,Storrs,CT 06269,U.S.A.

This paper presents an adaptive control scheme with an integration of sliding mode control into the L1adaptive control architecture,which provides good tracking performance as well as robustness against matched uncertainties.Sliding mode control is used as an adaptive law in the L1adaptive control architecture,which is considered as a virtual control of error dynamics between estimated states and real states.Low-pass filtering mechanism in the control law design prevents a discontinuous signal in the adaptive law from appearing in actual control signal while maintaining control accuracy.By using sliding mode control as a virtual control of error dynamics and introducing the low-pass filtered control signal,the chattering effect is eliminated.The performance bounds between the close-loop adaptive system and the closed-loop reference system are characterized in this paper.Numerical simulation is provided to demonstrate the performance of the presented adaptive control scheme.

L1adaptive control,sliding-mode control,matched uncertainties

DOI10.1007/s11768-015-3116-8

1 Introduction

Sliding mode control has been successfully implemented for nonlinear systems with matched uncertainties.In sliding mode control,trajectories of the system are forced to and maintained on the sliding surface.On the sliding surface,the system has a desired behavior,which is independent of matched uncertainties.Despite this robustness,the implementation of sliding mode control suffers from a chattering phenomenon characterized by oscillation of system trajectories around the sliding surface,which is due to the imperfections in switching devices and delays[1].In order to solve this chattering problem,a number of approaches have been proposed to improve sliding mode control.One approach is to replace the discontinuous control law with a continuous one by which the system motion is restricted within a boundary layer of the sliding surface[2,3].This boundary layer solution is a trade-off between control performance and chattering attenuation.Another approach to avoid chattering is higherorder sliding mode control in which the discontinuous control signal appears on the higher-order derivatives of the sliding variable instead of the first-order deriva-tive[4-6].Higher-order sliding mode approach requires higher-order derivatives of the sliding variable,which could be its limitation[7].Adding an integrator for sliding mode control signal is another approach to solve the chattering problem[8].In this approach,the sliding variable contains unknown disturbance as presented in[8],and therefore requires a disturbance estimator,which increases the complexity of sliding mode control design.

This paper presents an adaptive control scheme by introducing sliding mode control to the adaptive law design in the L1adaptive control architecture,which provides good tracking performance as well as robustness without introducing the chattering effect from the sliding mode control.The L1adaptive control is a variation of the model reference adaptive control with improved transient performance and handling of time-varying parameters and uncertainties.The architecture of the L1adaptive control consists of a state predictor,an adaptive law,and a control law.The adaptive law is used to update the parameters in the state predictor to make the estimated states arbitrarily close to the real states.The typical adaptive law design for the L1adaptive control includes projection-type adaptive law[9]and piece-wise constant adaptive law[10,11].In this paper,an alternative adaptive law design using sliding mode control is provided,which makes the state predictor provide a good estimation of real states independent of matched uncertainties.Chattering effect will not appear in the state predictor dynamics,since sliding-mode based adaptive law is used as a virtual control of error dynamics without any physical actuator involved.The initial states of error dynamics can be chosen on the sliding surface,which ensures robustness from the initial time and further improve the performance.The low-pass filtering design in the control law prevents a discontinuous signal in the adaptive law from appearing in the actual control signal while maintaining the control accuracy.By using sliding mode control as a virtual control of error dynamics and introducing the low-pass filtered control signal,the chattering effect is eliminated in the presented control scheme.

The contribution of this paper lies in two parts.The first part is that the L1adaptive control architecture can be borrowed by the sliding mode control for avoiding chattering effect.Instead of applying sliding mode control to the real plant,it is applied to the state predictor(virtual plant)to avoid the chattering effect while maintaining robustness against matched uncertainties.The second part is that the L1adaptive control architecture can have an alternative adaptive law design by using the sliding mode control.It shows the potential to use other aggressive control designs to fulfill the fast adaptation of the L1adaptive control architecture.Overall,the presented adaptive control scheme with sliding-mode based adaptive law demonstrates the merging of two control algorithms and provides a better understanding of the fast and robust adaptive mechanism.

The paper is organized as follows.Section2 gives the problem formulation.The L1adaptive control architecture with sliding-mode based adaptive law is presented in Section3.Stability and uniform performance bounds are given in Section4,while results are verified in Section5 through numerical simulation.Finally,Section6 concludes this paper.

2 Problem formulation

Consider the following uncertain dynamic system:

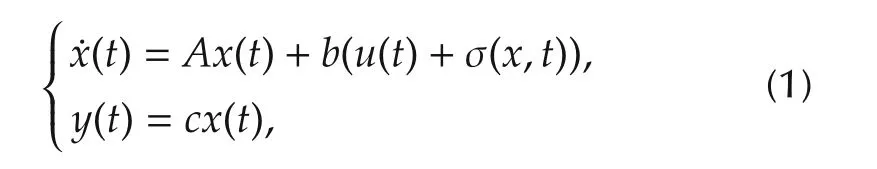
where x∈Rnis the system state vector,u∈R is the control signal,y∈R is the output,

with known positive constants a1,a2,...,an,b=[0 0···0 1]T,c ∈ Rnmakes c(-A)-1b nonzero,and σ(x,t)is an unknown function which represents the matched uncertainty.

Remark 1 For a general controllable linear time invariant system,there always exists a transformation in an appropriate coordinate system to make the system represented in the controllable canonical form in equation(1).The term σ(x,t)captures not only matched uncertainties but also the mismatch part that matrix A for actual plants does not have the same constants a1,a2,...,an.For a nonlinear system with nonlinear terms in the last row of matrix A in equation(1),it can always be transformed into a linear matrix A together with a nonlinear matched uncertainties σ(x,t).

Assumption1 The system is assumed to be control-lable,and rank(b)and rank(c)are nonzero.

Assumption 2 The unknown function σ(x,t)is assumed to be bounded and satisfy

where Φ(x,t)is a known function.

Assumption 3(Semiglobal Lipschitz condition) For any δ ＞ 0,there exist L(δ) ＞ 0 and B ＞ 0 such that|σ(x,t)-σ(¯x,t)|≤L(δ)‖x-¯x‖∞,|σ(0,t)|≤B,for all‖x‖∞≤δ and‖¯x‖∞≤δ uniformly in t.

The control objective is to design a full-state feedback controller to ensure that y(t)tracks the output of the desired system:

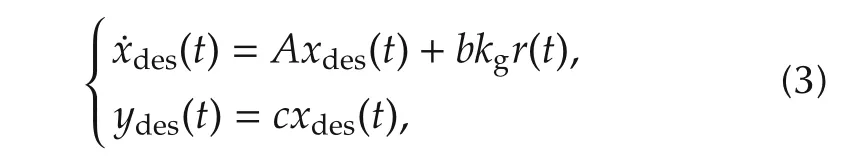
where kg=(c(-A)-1b)-1and r(t)is the reference signal.

3 L1adaptive control with sliding-mode based adaptive law

In this section,we develop an adaptive control architecture with sliding-mode based adaptive law for the sys-tem in(1).This architecture consists of three elements:state predictor,sliding-mode based adaptive law,and control law.The elements of this adaptive controller are introduced next.

State predictor

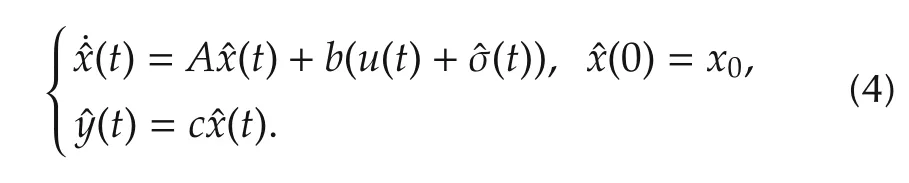
Let˜x=ˆx-xand˜y=ˆy-y.Then,weobtain the following error dynamics from(1)and(4):

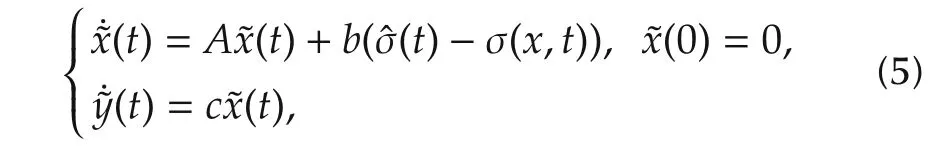
where the adaptive parameterˆσis governed by the following adaptation law.

Adaptive lawConsiderˆσas a virtual control signal in the error dynamics(5),and use sliding mode control method from[12]to designˆσas

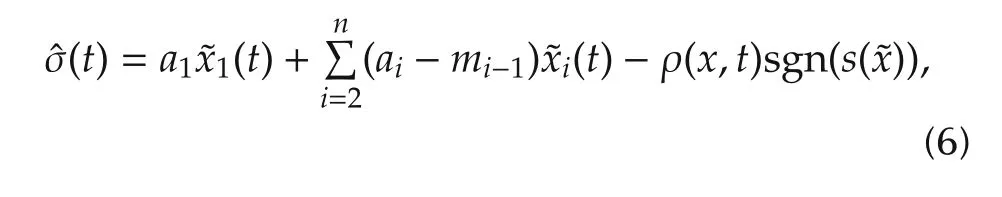
where xiis the ith component of states x,ρ(x,t)is defined asρ(x,t)≥Φ(x,t)+ηwith designed positive scalar η,s(˜x)represents the sliding surface and is defined as

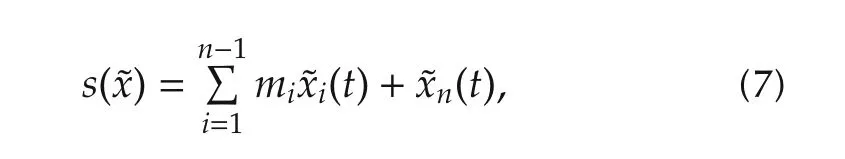
and the coefficients m1,m2,...,mn-1constitute a Hurwitz polynomial,which guarantees a stable reducedorder sliding motion.

Control law

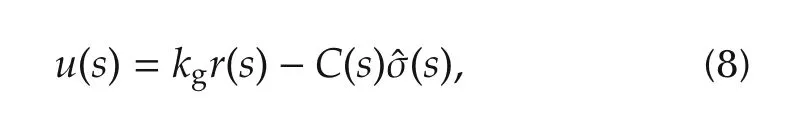
For the proof of stability and uniform performance bounds,the choice of k in the low-pass filter C(s)needs to ensure that there exists ρrsuch that

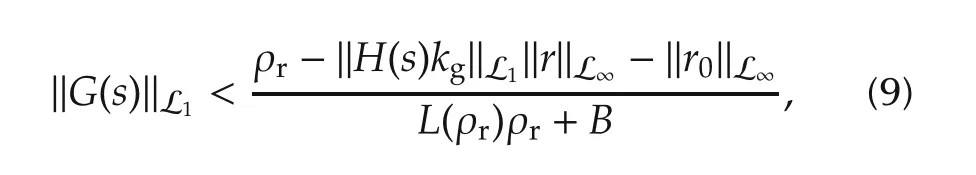
where H(s)=(sI-A)-1b,G(s)=H(s)(1-C(s)),r0=(sI-A)-1x0,L(ρr)is the Lipschitz constant as defined in Assumption 3,and B is defined in Assumption 3.

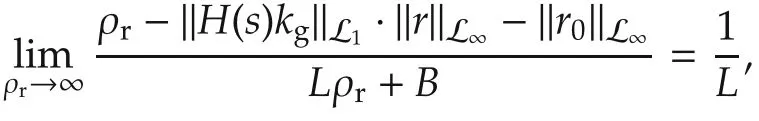
where ρris introduced in(9),and β is an arbitrary positive constant that satisfies ‖G(s)‖L1L(ρ) ＜ 1.Note that(9)implies that‖G(s)‖L1L(ρr) ＜ 1.Since L(ρ)depends continuously on ρ,‖G(s)‖L1L(ρ)＜ 1 can always be satisfied if β is small enough.

The L1adaptive controller consists of(4),(6)and(8)subject to stability condition(9).

4 Stability analysis

This section characterizes the estimation performance from state predictor,and provides the error bounds of both states and control input between the closed-loop adaptive system and the closed-loop reference system.

Lemma 1 For the system in(1)subject to Assumption 2,and the state predictor in(4),the adaptive law in(6)can make

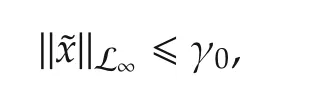
where γ0can be arbitrarily small.

Proof It follows from(5)and(7)that

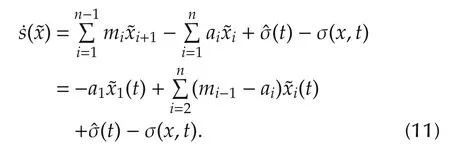
Substitution of adaptive law(6)into(11)yields

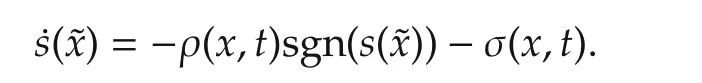
Consider the Lyapunov function candidate for the switching function s(˜x)as V=1 2s2(˜x).Then,

and note that s(0)=0 since˜x(0)=0 in(5),therefore trajectory of system starts at the sliding surface from the initial time and will be maintained on this sliding surface independent of matched uncertainties.On the sliding surface,the motion is governed by

Since the coefficients m1,m2,...,mn-1constitute a Hurwitz polynomial and˜x(0)=0,˜x(t)will stay on the convergence point˜x(0)=0 throughout the entire response of the system,which implies that there always exists an arbitrarily small constant γ0such that‖˜x‖L∞≤γ0,and concludes the proof. □

Then,we can further obtain¯x(t)=eAmt¯x(ts).It means that¯x(t)exponentially converges to zero,which implies that˜x also exponentially converges to zero.The rate of convergence can be adjusted by choice of m1,m2,...,mn-1in(7).

Next,we give the definition and stability analysis of the closed-loop reference system,and characterize the error bounds between the closed-loop reference system and the closed-loop adaptive system.

We define the closed-loop reference system with the nonadaptive control law as follows:

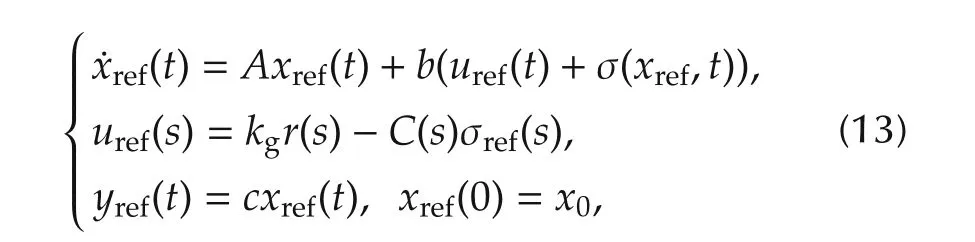
where σref(s)is the Laplace transformation of σ(xref,t).

Lemma 2 For the closed-loop reference system in(13)subject to the stability condition(9),if‖x0‖∞＜ ρr,then we have

where ρris introduced in(9),and ρur=|kg|·‖r‖L∞+‖C(s)‖L1(L(ρr)ρr+B).

ProofWe prove the bound in(14)by contradiction.If(14)is not true,since ‖x0‖∞＜ ρrand xref(t)is continuous,there exists t?such that ‖xref(t?)‖= ρrwhile‖xref(t)‖＜ ρr,∀t∈ [0,t?),which implies that

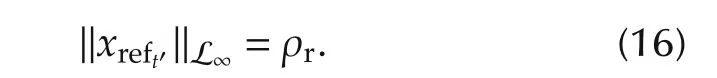
It follows from(13)that

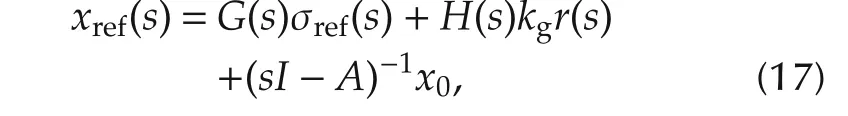
where H(s)=(sI-A)-1b and G(s)=H(s)(1-C(s)).Example 5.2 in[1,Page 199]implies that

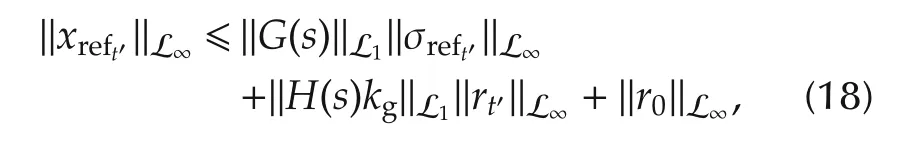
where r0=(sI-A)-1x0.Using Assumption 3 and the upper bound in(16),we arrive at the following upper bound:

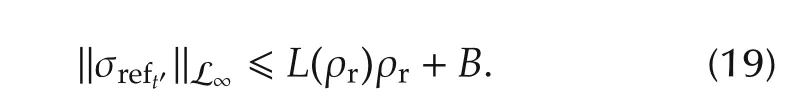
The derivation of equation(19)uses the fact that‖rt?‖L∞≤ ‖r‖L∞.Substitution of(19)into(18)yields

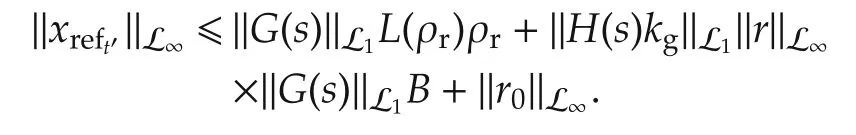
The stability condition(9)can be solved for ρrto obtain the following upper bound:

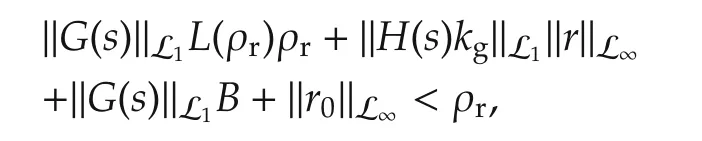
which implies that‖xreft?‖L∞≤ ρrand contradicts(16).This proves(14),which further implies that‖σreft?‖L∞＜L(ρr)ρr+B holds for all t with strict inequality.Therefore,it follows from the definition of uref(s)in(13)that

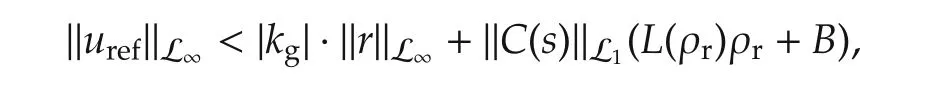
which proves(15),and concludes the proof. □

Theorem 1 Given the closed-loop system with the L1adaptive controller defined via(4),(6),and(8),subject to the stability condition in(9),and the closed-loop reference system in(13),if‖x0‖∞＜ ρr,then

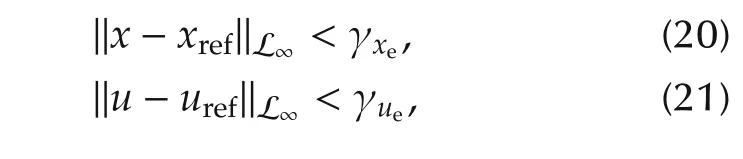
where

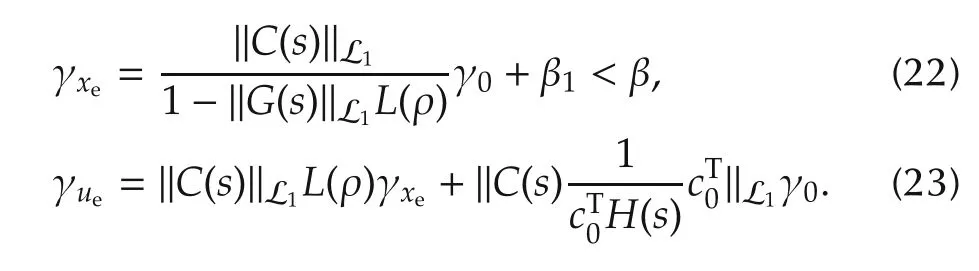
γ0is introduced in Lemma 1,which can be arbitrarily small,β1is an arbitrarily small positive constant,and β is introduced in(10).

Proof(By contradiction) Assume that(20)and(21)are not true.Then,since ‖x(0)-xref(0))‖∞=0 ＜ γxe,‖u(0)-uref(0))‖∞=0 ＜ γue,and x(t),xref(t),u(t),and uref(t)are continuous,there exists t?such that‖x(t?)-xref(t?))‖∞＜ γxe,or ‖u(t?)-uref(t?))‖∞＜ γue,while ‖x(t)-xref(t))‖∞＜ γxeand ‖u(t)-uref(t))‖∞＜ γuefor all t∈[0,t?),which implies that

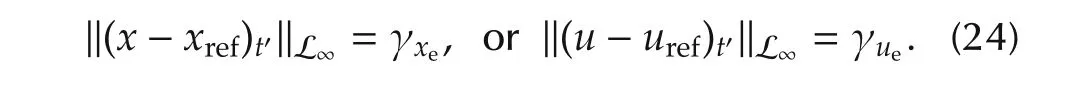
From Lemma 2,we have

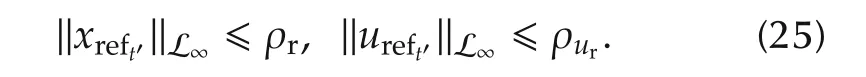
It follows from(10),(22)and the bounds in(24)and(25)that

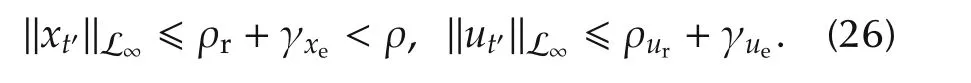
The Laplace transformation of the system in(1)is

where σ(s)is the Laplace transformation of σ(t),and ˜σ(s)=ˆσ(s)-σ(s).Let e(t)=x(t)-xref(t).From(17)and(27),we obtain

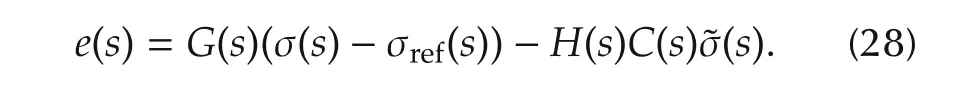
It follows from(4)that

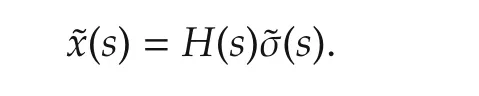
Then,equation(28)becomes

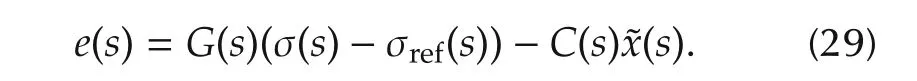
Assumption 3 and bounds in(25)and(26)yield

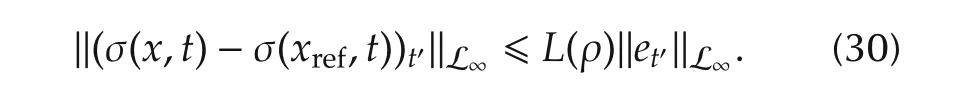
Following from(29)and(30),we further obtain

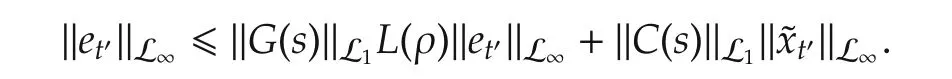
It follows from Lemma 2 and Remark 2 that

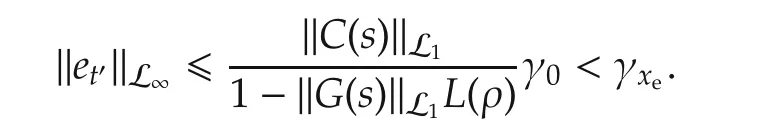
From the definition in(8)and control law using in(13)one can derive

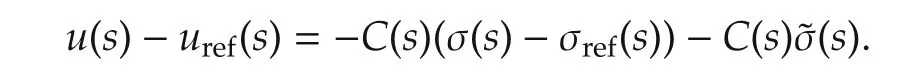
It follows from Lemma 4 in[13]that there exists c0∈Rnsuch that

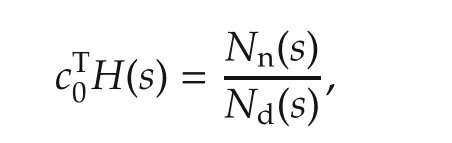
where the order of Nd(s)is one more than the order of Nn(s),and both Nn(s)and Nd(s)are stable polynomials.Then,we have C(s)˜σ(s)=Since C(s)is stable and strictly proper,the complete system C(s)is proper and stable,which implies that its L1gain exists and is finite.Hence,we have the following upper bound:

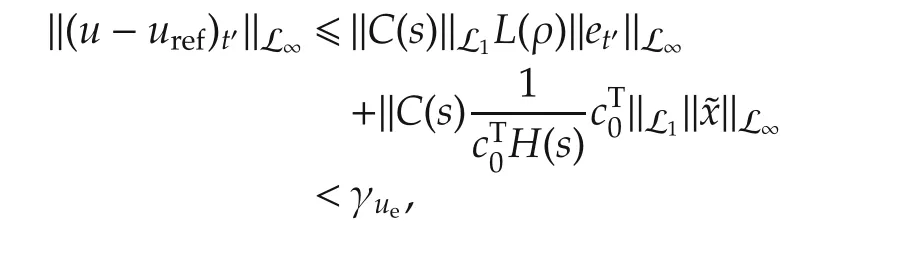
which proves(21),and concludes the proof. □

Remark4 The error bounds between x(t)andxref(t),and u(t)and uref(t)are uniformly bounded,and can be arbitrarily small.To understand how these bounds can be used for ensuring response with desired specifications,consider the following ideal control signal udes(t)=kgr(t)-σ(x,t),which leads to the desired system in(3)by canceling the uncertainties exactly.In the closed-loop reference system(13),the uncertainties term in the control law is low-pass filtered by C(s).Thus,the closed-loop reference system has a different response as compared with the desired one(3).The response of x(t)can be made as close as desired to(3)by increasing the bandwidth of the low-pass filter C(s).

5 Simulation

In this section,two different simulation scenarios will be provided to demonstrate the performance of the L1adaptive control with sliding-mode based adaptive law.

For the L1-SMC design,switching function and ρ(x)in adaptive law are chosen as=and+10,and the low-pass filter in the control law is chosen as C(s)=For the SMC design,switching function and ρ(x,t)use the same parameters as the ones using in the L1-SMC design.In order to achieve reference tracking,a reference input filter[14,15],¯r=kgr with kgdefined in equation(3),is introduced for the SMC design.

The closed-loop response of L1-SMC and SMC are shown in Figs.1-6,respectively.As shown in Figs.1and 5,the output y(t)is coincide with the desire system’s output ydes(t)under L1-SMC and SMC,which demonstrates good tracking performance.Yet,SMC generates an oscillating control signal(shown in Fig.6)to achieve tracking,while L1-SMC generates a smooth control signal(shown in Fig.4).The smooth control signal is due to the low-pass filtering design and sliding-mode based virtual control.For L1-SMC,all states x(t)in Fig.2 are stabilized and the estimation errors˜x(t)in Fig.3 have very small values.The estimation errors˜x represent errorsbetween the state predictor in equation(4)and plant(1).The small estimation errors demonstrate good estimation by using sliding-mode based adaptive law.

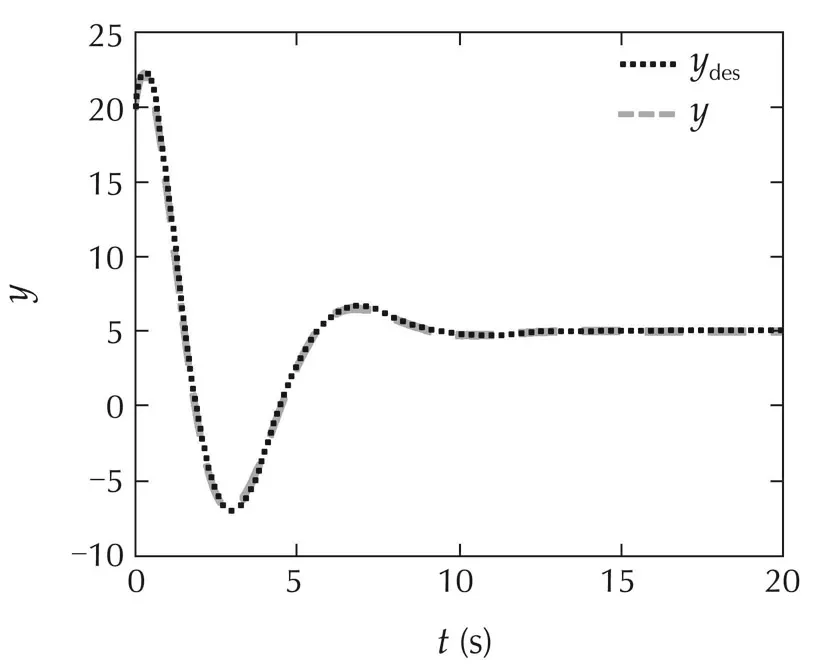
Fig.1 Scenario 1:Output of the closed-loop system with L1-SMC.

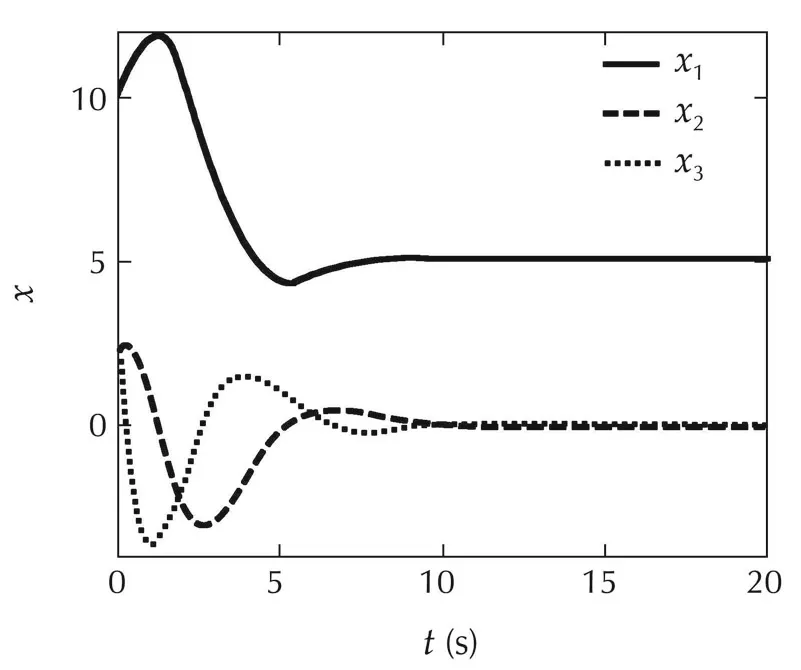
Fig.2 Scenario 1:States of the closed-loop system with L1-SMC.

Fig.3 Scenario 1:Estimation errors between state predictor and plant with L1-SMC.

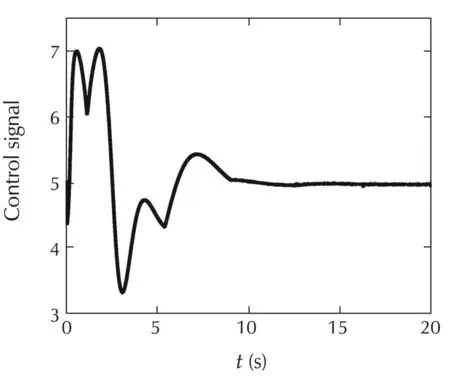
Fig.4 Scenario 1:Control signal of the closed-loop system with L1-SMC.

Fig.5 Scenario1:Output of the closed-loop system with SMC.

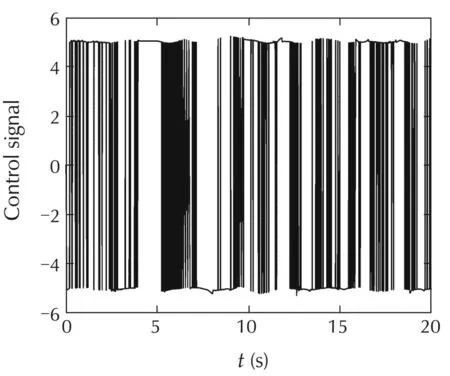
Fig.6 Scenario 1:Control signal of the closed-loop system with SMC.

Scenario 2(L1-SMC for systems with nonlinear dynamics and stable zero dynamics) Consider a nonlinear system with stable zero dynamics as follows:

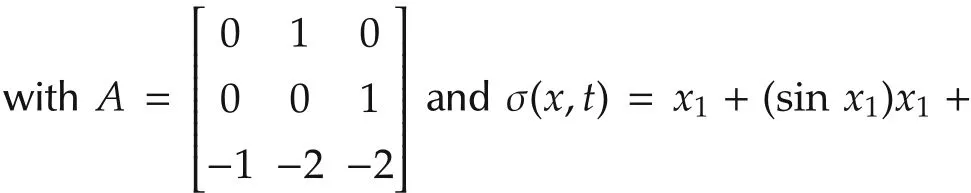
For the L1-SMC design,switching function and ρ(˜x,t)in adaptive law are chosen as s(˜x)=5˜x1+˜x2+˜x3and ρ(˜x,t)=5‖˜x‖+10,and the low-pass filter in the control law is chosen as C(s)=50/(s+50).

The simulation results of L1-SMC for the nonlinear system with stable zero dynamics are shown in Figs.7-10.The output y(t)is coincide with the desire system’s output ydes(t)in Fig.7,which demonstrates good tracking performance.At the same time,all states x(t)are stabilized as shown in Fig.8.

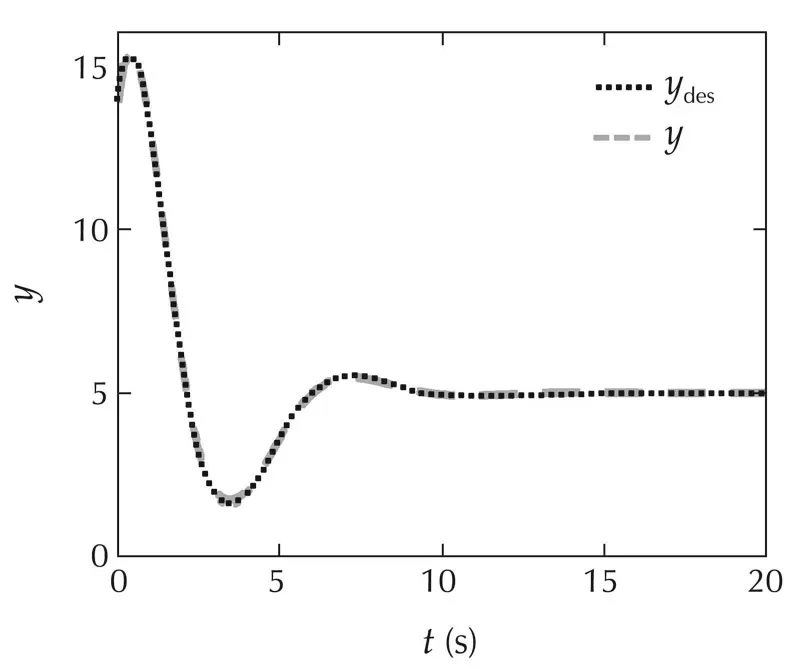
Fig.7 Scenario 2:Output of the closed-loop system with L1-SMC.

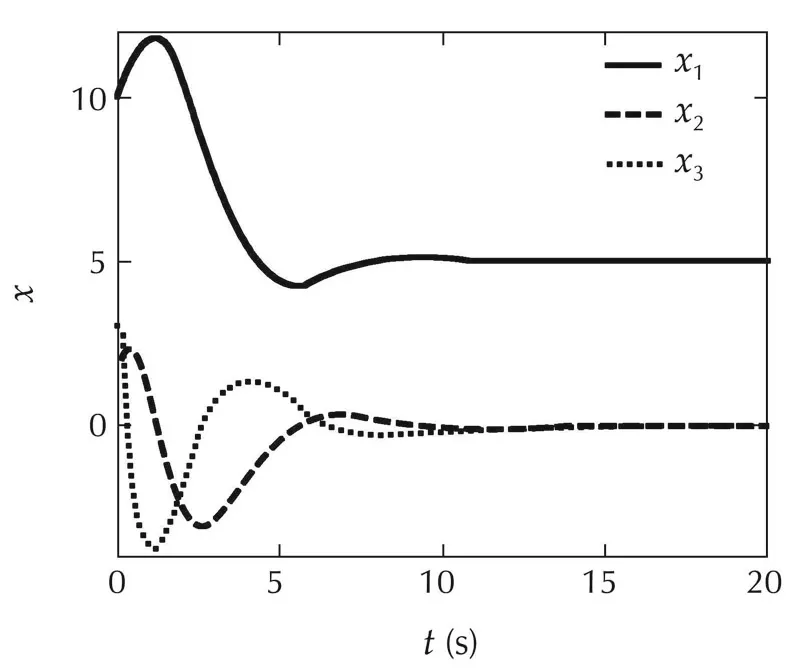
Fig.8 Scenario 2:States of the closed-loop system with L1-SMC.

The estimation errors˜x as shown in Fig.9 have very small values,which demonstrates good estimation by using sliding-mode based adaptive law.In Fig.10,the control signal is smooth.

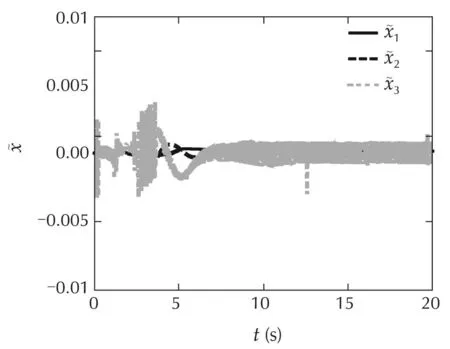
Fig.9 Scenario 2:Estimation errors between state predictor and plant with L1-SMC.

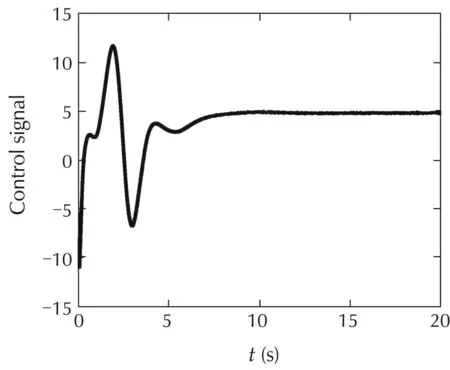
Fig.10 Scenario 2:Control signal of the closed-loop system with L1-SMC.

6 Conclusions

In this paper, an adaptive control scheme with sliding-mode based adaptive law is presented.The robustness and control accuracy of sliding mode control are preserved while chattering effect is not introduced.The traditional sliding mode control is used as adaptive law in the L1adaptive control architecture,which is a virtual control of error dynamics between estimated states and real states.The error bounds between estimated states and real states are bounded which can be arbitrarily small.The low pass filtering design in the control law prevents discontinuous signal in the adaptive law from appearing in the actual control signal while stillmaintain-ing control accuracy.The norm bounds of both states and control signals between the closed-loop adaptive system and the closed-loop reference system are characterized.Numerical simulation results demonstrate the performance of the presented adaptive control scheme.

[1]H.K.Khalil.Nonlinear Systems.3rd ed.Upper Saddle River:Prentice Hall,2002.

[2] J.J.Slotine,S.S.Sastry.Tracking control of non-linear systems using sliding surfaces,with application to robot manipulators.International Journal of Control,1983,38(2):465-492.

[3]K.D.Young,V.I.Utkin,U.Ozguner.A control engineer’s guide to sliding mode control.IEEE Transactions on Control Systems Technology,1999,7(3):328-342.

[4] G.Bartolini,A.Ferrara,E.Usani.Chattering avoidance by second-order sliding mode control.IEEE Transactions on Automatic Control,1998,43(2):241-246.

[5] A.Levant.Sliding order and sliding accuracy in sliding mode control.International Journal of Control,1993,58(6):1247-1263.

[6] A.Levant.Universal single-input-single-output(SISO)sliding mode controllers with finite-time convergence.IEEE Transactions on Automatic Control,2001,46(9):1447-1451.

[7] G.Bartolini,A.Pisano,E.Punta,et al.A survey of applications of second-order sliding mode control to mechanical systems.International Journal of Control,2003,76(9/10):875-892.

[8]M.L.Tseng,M.S.Chen.Chattering reduction of sliding mode control by low-pass filtering the control signal.Asian Journal of Control,2010,12(3):392-398.

[9]C.Cao,N.Hovakimyan.Design and analysis of a novel L1adaptive control architecture with guaranteed transient performance.IEEE Transactions on Automatic Control,2008,53(2):586-591.

[10]C.Cao,N.Hovakimyan.L1adaptive output-feedback controllerfornon-strictly-positive-real reference systems:missile longitudinal autopilot design.Journal of Guidance,Control,and Dynamics,2009,32(3):717-726.

[11]J.Luo,C.Cao,Q.Yang.L1adaptive controller for a class of non-affine multi-input multi-output nonlinear systems.International Journal of Control,2013,86(2):348-359.

[12]C.Edwards,S.K.Spurgeon.Sliding Mode Control:Theory and Applications.Bristol:Tayloramp;Francis,1998.

[13]C.Cao,N.Hovakimyan.Guaranteed transient performance with L1adaptive controller for systems with unknown time-varying parameters and bounded disturbances:Part I.Proceedings of the American Control Conference,New York:IEEE,2007:3925-3930.

[14]W.S.Levine.The Control Handbook.Boca Raton:CRC Press,1996.

[15]J.Luo,X.Zou,C.Cao.Eigenvalue assignment for linear time-varying systems with disturbances.IET Control Theoryamp;Applications,2012,6(3):365-374.

16 July 2013;revised 2 May 2015;accepted 4 May 2015

†Corresponding author.

E-mail:jie.luo@outlook.com.

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg

Jie LUO received his Ph.D.in Mechanical Engineering from University of Connecticut,Storrs,CT,in 2013.He received his B.Sc.and M.Sc.degrees in Department of Control Science and Engineering from Huazhong University of Science and Technology,Wuhan,China,in 2006 and 2008,respectively.His research interests include theory and applications of adaptive control,nonlinear control,and cooperative control.E-mail:jie.luo@outlook.com.

Chengyu CAO is an associate professor of mechanical engineering at the University of Connecticut.He joined the University of Connecticut in 2008.Prior to that,he was a research scientist in the Department of Aerospace and Ocean Engineering at Virginia Polytechnic Institute and State University.He received his Ph.D.in Mechanical Engineering from the Massachusetts Institute of Technology in 2004.He earned his B.Sc.degree in Electronics and Information Engineering from Xian Jiaotong University,China,and M.Sc.in Manufacturing Engineering from Boston University in 1995 and 1999,respectively.His research interests are in the areas of dynamics and control,adaptive and intelligent systems,and mechatron-ics,with a focus on unmanned systems and aerospace applications.E-mail:ccao@engr.uconn.edu.