Optimal control of quantum systems with SU(1,1)dynamical symmetry

Wenbin DONG,Rebing WU†,Jianwu WU,Chunwen LI,Tzyh-Jong TARN

1.Department of Automation,Tsinghua University,Beijing 100084,China;

2.Center for Quantum Information Science and Technology,Tsinghua National Laboratory for Information Science and Technology(TNlist),Beijing 100084,China;

3.Beijing Aerospace Automatic Control Institute,Beijing 100854,China;

4.Electrical and Systems Engineering Department,Washington University in St.Louis,St.Louis,Missouri 63130,U.S.A.

Optimal control of quantum systems with SU(1,1)dynamical symmetry

Wenbin DONG1,2,Rebing WU1,2†,Jianwu WU3,Chunwen LI1,2,Tzyh-Jong TARN2,4

1.Department of Automation,Tsinghua University,Beijing 100084,China;

2.Center for Quantum Information Science and Technology,Tsinghua National Laboratory for Information Science and Technology(TNlist),Beijing 100084,China;

3.Beijing Aerospace Automatic Control Institute,Beijing 100854,China;

4.Electrical and Systems Engineering Department,Washington University in St.Louis,St.Louis,Missouri 63130,U.S.A.

SU(1,1)dynamical symmetry is of fundamental importance in analyzing unbounded quantum systems in theoretical and applied physics.In this paper,we study the control of generalized coherent states associated with quantum systems with SU(1,1)dynamical symmetry.Based on a pseudo Riemannian metric on the SU(1,1)group,we obtain necessary conditions for minimizing the field fluence of controls that steer the system to the desired final state.Further analyses show that the candidate optimal control solutions can be classified into normal and abnormal extremals.The abnormal extremals can only be constant functions when the control Hamiltonian is non-parabolic,while the normal extremals can be expressed by Weierstrass elliptic functions according to the parabolicity of the control Hamiltonian.As a special case,the optimal control solution that maximally squeezes a generalized coherent state is a sinusoidal field,which is consistent with what is used in the laboratory.

Quantum control,optimal control,dynamical symmetry DOI10.1007/s11768-015-4128-0

1 Introduction

In theoretical physics,the SU(1,1)dynamical symmetry is of fundamental importance in algebraically solving Schr¨odinger equations with various potential functions(e.g.,Morse potential,P¨oschl-Teller potential,and Coulomb potential)[1-5],as well as in solid-state[6]and optical systems[7].As one of the simplest Lie groups,SU(1,1)group can be taken as an analytic continuation of SU(2)group and the Heisenberg group H(1)[8],but its noncompactness makes it more useful in generating unbounded and continuous energy spectrum in infinite-dimensional quantum mechanical systems[8-10].

Analogous of the role of SU(2)dynamical symmetry in quantum information science,quantum systems with SU(1,1)dynamical symmetry are basic building blocks in advanced quantum technologies[11],e.g.,quantum squeezed lights and nanoscale mechanical resonators[12,13],molecular disassociation/association control[14],high harmonic generation and continuous-variable quantum information[15,16].These applications lead to many control problems in engineering desired state or gate operations[14],which are generally realized by manipulating an electromagnetic field that directly or indirectly interacts with the system.Incorporated with the underlying physical disciplines,modern control theory[17]was recently introduced to design controls used in quantum chemistry[14,18]and quantum information[16,19].In particular,the optimal control theory based on variational analysis(later extended to the so-called Maximum Principle to treat more general constraints)have been widely explored in quantum systems with both numerical and experimental applications.

In this paper,we study the minimum-fluence control problem for systems with SU(1,1)dynamical symmetry,which is motivated by the common limitations on available control resources.For example,dynamical processes in nonlinear optical systems can only experience a very short period of time for effective interaction(e.g.,in an optical crystal or an optical fiber),within which the control field has to be sufficiently strong to achieve the control goals.However,the power of realistic control resources is often limited;even if this is not a severe restriction,strong controls may introduce unwanted noises via excitation of environmental modes.Therefore,it is demanding to efficiently exploit the limited control bandwidth(jointly determined by available control power and pulse length) to achieve control goals.When the interaction time is fixed (e.g., in an optical fiber with fixed length),the use of control bandwidth can be optimized by minimizing the control fluence.To the authors’knowledge,there are some relevant studies on classical mechanical systems evolving on the SU(1,1)group(e.g.,non-Euclidean elastica[20-24]),but the applications to quantum systems have been rarely seen in the literature.

The balance of this paper is organized as follows.In Section 2,we introduce the model of quantum control systems with SU(1,1)dynamical symmetry.In Sections 3 and 4,we derive the conditions for minimum-fluence control for systems with one or two controls,based on which the properties of the candidate optimal control solutions are discussed.Finally,conclusions are drawn in Section 5.

2 Quantum control systems with SU(1,1)dynamical symmetry

Consider a quantum control system whose state is in a Hilbert space H.When the field can be approximated as a classical field(e.g.,an optical pulse that contains a sufficient large number of photons),we can describe the system with the following semiclassical model[25]:

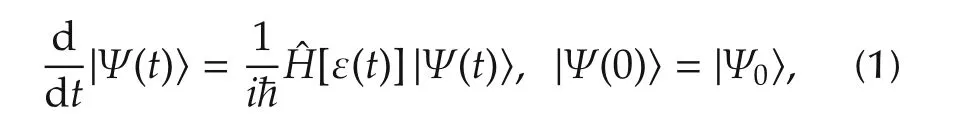
where the time-dependent state|Ψ(t)? ∈ H is governed by the Hamiltonian involving the control field ε(t).

The quantum control system(1)is said to possess SU(1,1)dynamical symmetry if the Lie algebra generated by the set of controlled HamiltoniansˆH[ε(t)]for all ε(t)is isomorphic to su(1,1)(see the following discussion for details),thereby generate a Lie semigroup of unitary propagators contained in SU(1,1).Next,we will provide definitions of SU(1,1)group,its Lie algebra and the corresponding generalized SU(1,1)coherent states.To facilitate the following optimal control studies,the two control systems will be introduced in the context of quantum optics.

2.1 SU(1,1)Lie group and SU(1,1)coherent-state representation

The real Lie groups SU(2)and SU(1,1)can be uniformly defined[20]as the set of all 2×2 matrices that satisfy X†PX=P,where

with?=1 for SU(2)and?=-1 for SU(1,1),respectively.Correspondingly,the Lie algebras of these two groups consists of 2×2 skew P-Hermitian matrices AP=-A,where the P-adjoint of X is defined as XP=PX†P.Both Lie algebras of SU(1,1)and SU(2)are three dimensional[26],and the elements in the Lie algebra satisfy XP=-X,and the infinitesimal generators satisfy the following commutation relationships:

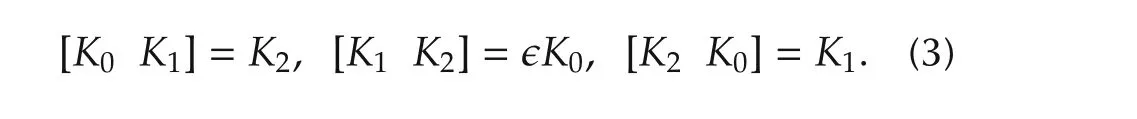
A standard realization of the above basis is as follows:

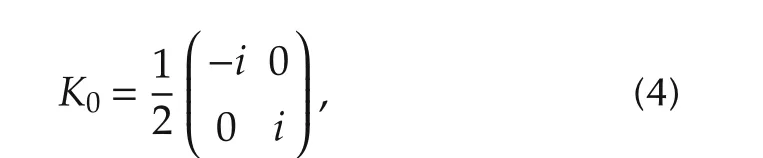
Although being defined in a unified manner,SU(2)and SU(1,1)are essentially distinct in that SU(2)is a compact group but SU(1,1)is noncompact.This can be seen from the associated quadratic form

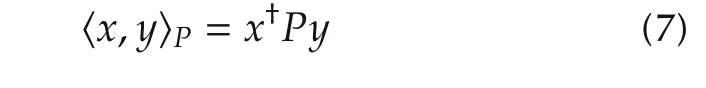
on C2induced by the P-adjoint.For the elements A and B in the Lie algebras su(1,1),we have

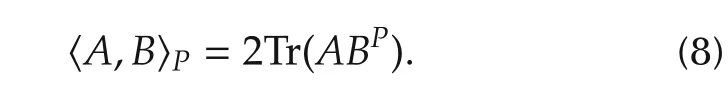
The quadratic form for SU(2)is the same as the standard matrix inner products.However,the quadratic form for SU(1,1)is not positive definite and thus is not an inner product,which is due to the noncompac-tness of SU(1,1).Nevertheless,their invariance under the SU(1,1)transformations is very useful in the following studies.For convenience,we call them pseudo inner products,many of whose calculations are parallel with those for SU(2).For example,if X,Y and Z are skew P-Hermitian,then

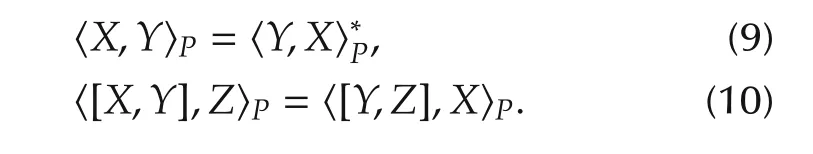
Based on the pseudo inner product defined on su(1,1),one can further classify its elements according to their geometry.A matrix M∈su(1,1)and its exponential eMare said to be elliptic(hyperbolic,parabolic)if?M,M?Pis positive(negative,zero).For examples,in the basis(4),K0is elliptic,while K1and K2are hyperbolic.

For quantum systems possessing SU(1,1)dynamics symmetry,the evolution operator acting on the Hilbert space H forms a unitary representation of elements in su(1,1).Due to the noncompactness of SU(1,1),the Hilbert space H carrying such representations must be infinite dimensional.This feature makes essential distinctions between SU(1,1)and SU(2)in that SU(1,1)can serve to generate energy spectrum of an unbounded system but SU(2)can only be applied to bounded systems.

The unitary representation also induces an isomorphic transformation,say R,from the Hamiltonian operator ˆH to a skew P-Hermitian matrix in su(1,1).It is easy to verify that the following equalities hold for arbitrary X,Y∈su(1,1):

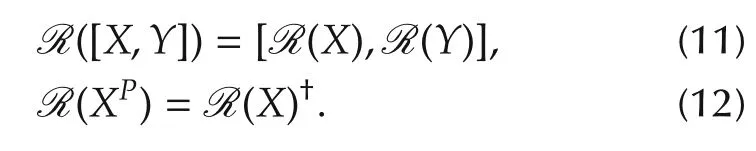
In this paper,we are concerned with the control of an important class of quantum states,namely the SU(1,1)generalized coherent states(GCS),which are generalized from the coherent states of a quantum harmonic oscillator.According to the standard Perelomov’s definition[27],an SU(1,1)GCS is some quantum state that can be generated by some SU(1, 1) transformation in the following way:

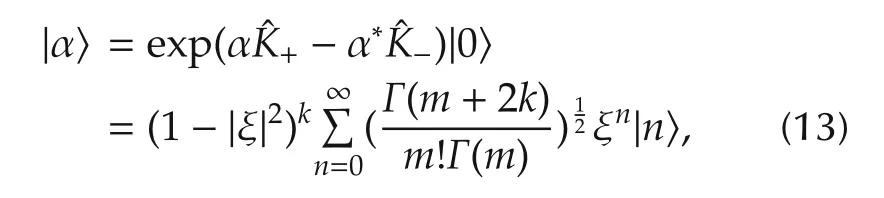
whereˆK±=R(K1±iK2)is a given unitary representation of su(1,1);and{|0?,|1?,...,|n?,...}are the orthonormal basis of H with|0?being an arbitrary state in the Hilbert space(e.g.,the vacuum state).The integer k is some constant that labels the specific Hilbert space.The set of GCSs generated from a fixed state|0?is invariant under SU(1,1)transformations,and they form a two-dimensional submanifold that is isomorphic to the coset space SU(1,1)/U(1),where U(1)is the one dimensional Lie group generated by K0.

2.2 Quantum optical control systems with SU(1,1)dynamical symmetry

The Hamiltonian of the control system(1)generally possesses the following form[28,29]:

whereˆH0andˆH1are the internal and control Hamiltonians.The classical control field is a scalar real time dependent function with tunable amplitude.In atomic or molecular control,ˆH1represents the electric(or magnetic)dipole that is coupled to an electric(or magnetic)field.Particularly,for the manipulation of quantum optical modes in a cavity or some dielectric medium,the control is realized by a pump field.

For example,two-photon processes are used for single mode squeezing with free and control Hamiltonians being[30-32]:

where the annihilation operatorˆa of the optical mode to be squeezed is defined on the Fock space spanned by photon number states{|0?,|1?,...}.Another circumstance is applying the degenerate parametric down conversion corresponding to the following two-mode squeezing:

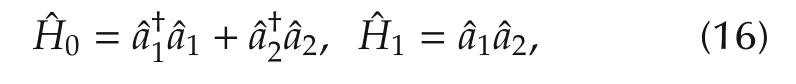
whereˆa1andˆa2are the annihilation operators of the two created photons.In the two examples,the involved sets of operators satisfy the commutation relationship(3)when taking

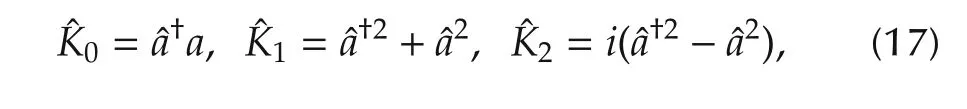
or

Systems(15)and(16)describe optical systems coupled with a linearly polarized field.When the field is circularly polarized,the Hamiltonian has the following form:

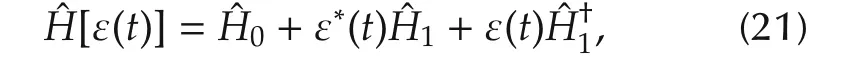
where the value of the control field parameter ε(t)is a complex number.Quantum control systems with one or two controls are to be studied in the following sections.

3 Minimum-f l uence coherent state transfer with single control

As mentioned above,quantum control systems with SU(1,1)dynamical symmetry evolve on a finite dimensional manifold of generalized coherent states in the(infinite-dimensional)Hilbert space.Using the unitary representation R defined above,we can map the quantum state|Ψ(t)?to a two-dimensional complex vector in C2:

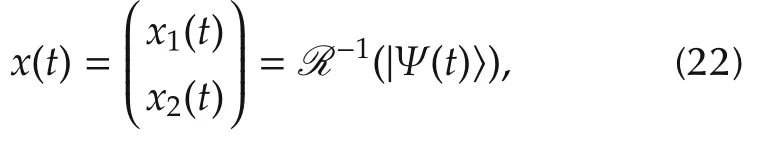
where[1 0]Tcorresponds to the root state|0?in(13).Correspondingly,the Hamiltonian H[ε(t)]is mapped to a 2×2 skew P-Hermitian matrix

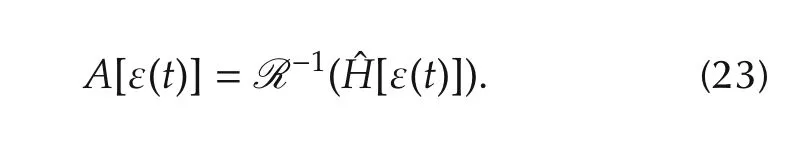
It is obvious that a control field ε(t)drives system(1)from|Ψ0?to|Ψf?if and only if the same control drives the following system:

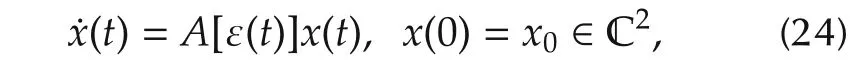
from x0=R-1(|Ψ0?)to xf=R-1(|Ψf?).Thus,it is more convenient to study optimal control problems with this finite-dimensional system.

The field fluence to be minimized is defined by the following cost functional:

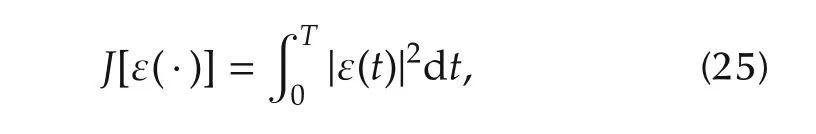
over the set of controls that are L2-integrable over a fixed time period[0,T].The Schr¨odinger equation(or the isomorphic one(24))forms a dynamical constraint for the optimization.

Next,we apply the famous Pontrygin Maximum Principle[33,34]to study the minimum-fluence control problem for systems with SU(1,1)dynamical symmetry.Consider a quantum system controlled by a single field,which by the isomorphic transformation R defined above,is translated to a two-dimensional optimal control system problem as follows:

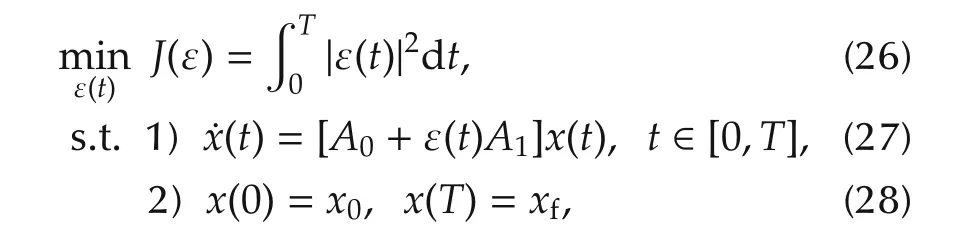
where both A0and A1are skew P-Hermitian.The initial x(0)=x0and boundary condition x(T)=xfare fixed,whereas T is not fixed.

First,we define the following pseudo Hamiltonian:

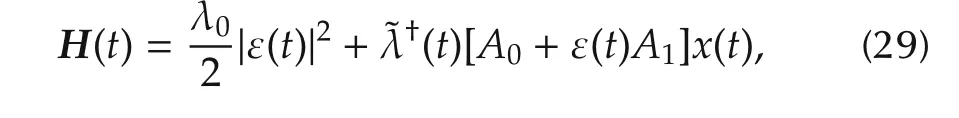
whereλ0=0or1.The first term corresponds to the cost functional to be minimized,and the second term to the dynamical constraint(26)with a Lagrangian multiplier ˜λ(t).By defining λ(t)=P˜λ(t),we have

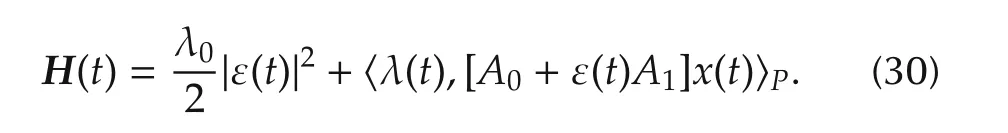
The evolution of the Lagrangian multiplier is derived as follows:

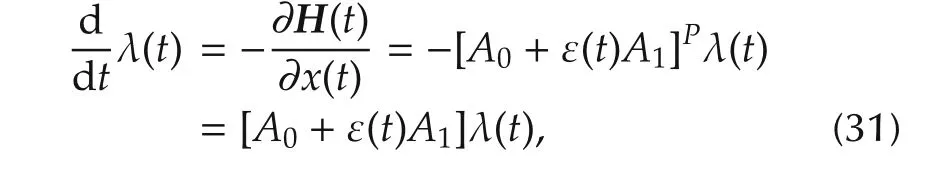
whose boundary conditions are to be determined by the initial and boundary conditions in equation(28).

According to the Maximum Principle[34,35],any optimal control ε(t)that minimizes the cost functional(25)must be an extremal curve that is defined as a control function satisfying

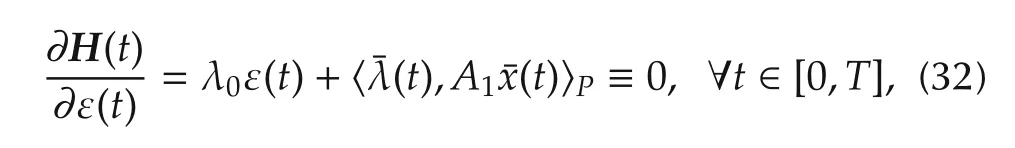
where the extremal trajectory(¯x(t),¯λ(t))is generated by the candidate optimal control ε(t).The extremals corresponding to λ0=1 are called normal,otherwise the extremals corresponding to λ=0 are called abnormal[19].

To further determine the optimal control from the condition(32),we introduce the following auxiliary variables:

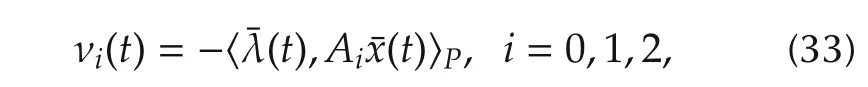
where A2=[A0A1].By differentiating these variables in time,we obtain(a.e.)

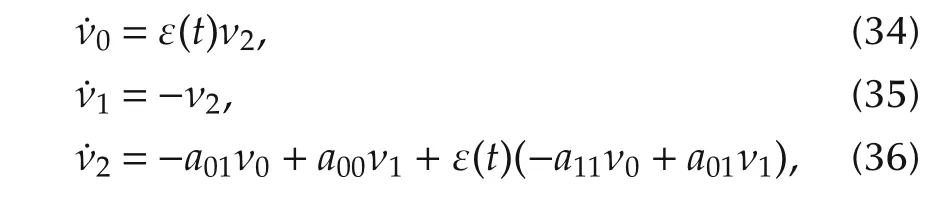
where the structural constants a00,a01and a11are defined as

Equations(34)-(36)have a first integral

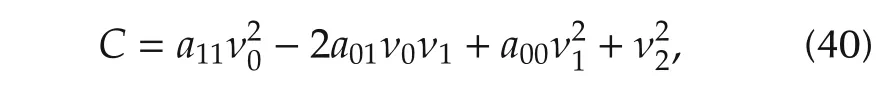
which is constant during the evolution and thereby restricts the trajectory(ν0(t),ν1(t),ν2(t))on a two dimensional surface C=const.This surface can be an ellipsoid,a hyperboloid,a paraboloid or a cone,which corresponds to the cases that A2is elliptic,hyperbolic,parabolic or conic,respectively.Next,we will use equations(34)-(36)to analyze the properties of abnormal and normal extremals.

3.1 Abnormal extremals

Abnormal extremals are defined as control solutions that satisfy(32)for λ0=0,which correspond to the case that the cost is overwhelmed by the dynamical constraint.We have the following conclusions.

Theorem 1 If A1is non-parabolic,then there exists a unique abnormal extremal ε(t)=

Proof By the definition of abnormal extremals,i.e.,λ0=0,condition(32)becomes

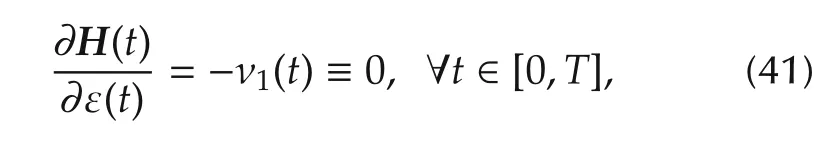
which also implies that ν0(t)is constant because the pseudo Hamiltonian H(t)= ν0(t)+ ε(t)ν1(t)is timeinvariant during the evolution.Further,equation(41)can be differentiated to yield ν2(t)≡ 0.

Differentiating again ν2(t)≡ 0,we have from which it is easy to see that,when a11≠0(i.e.,A1is non-parabolic),the abnormal control is a constant ε(t)=-□

3.2 Normal extremals

The normal extremals correspond to λ0=1.With respect to such extremals,the second-order derivative of the pseudo Hamiltonian reads

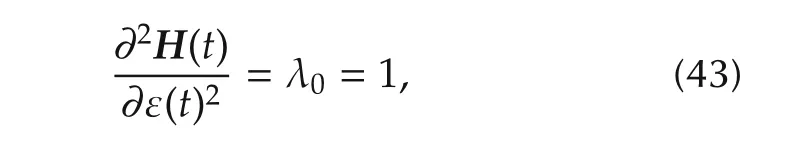
which implies that the corresponding control is always a local minimum.The necessary condition for candidate optimal controls can be expressed as ε(t)= ν1(t),and thus we have(a.e.)

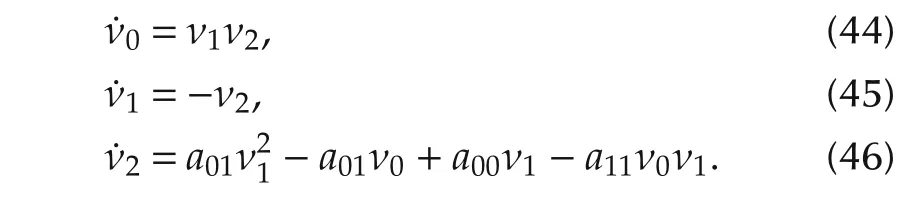
In addition to the first integral(40),we have found that these equations possess another first integral E=.This quantity is called the elastic energy in[20].

The properties of normal extremals are essentially determined by the geometry of the parabolicity of A1.

1)When the control Hamiltonian is non-parabolic,i.e.,andε˜(t)=ε(t)with which equation(26)is transformed to be

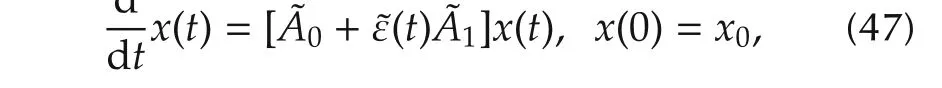
where one can examine that˜a01=?˜A0,˜A1?P=0.Thus,without loss of generality,we can always assume that a01=0,under which the first integrals becomes

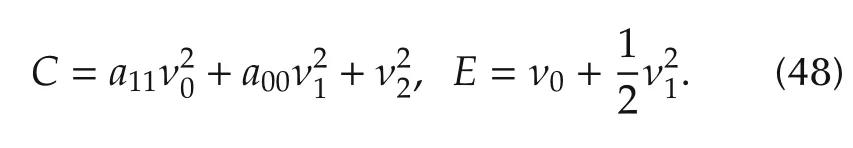
Then equations(44)-(46)can be reduced to a first-order differential equation

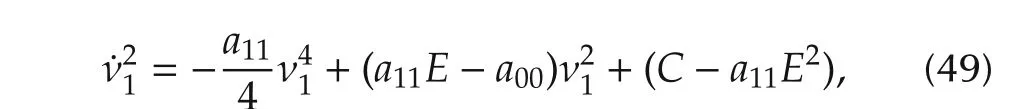
which,under the variable replacement zleads to the following equation:

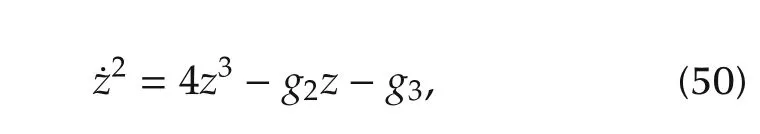
where g2and g3are functions of the constants E and C.

2)When the control Hamiltonian is parabolic,i.e.,a11=0,we find that under the following transformation:

Similarly,let ν1=equations(44)-(46)can be reduced to the same first-order differential equation

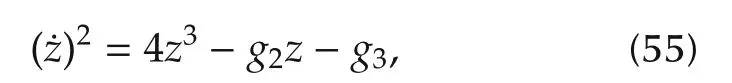
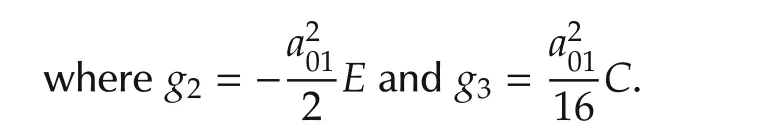
The above analysis shows that the normal extremals can be solved from the same differential equation(50),whose solution belongs to the class of Weierstrass elliptic functions[36],and the parameters g2and g3can be determined by the boundary conditions x(0)=x0,x(T)=xfand the final time pseudo Hamiltonian condition H(T)=0.In particular,we can get more explicit solutions for the case that A2is parabolic.In[25],it was proven that A2is parabolic if and only if=0.Moreover,in this case,A2must be a linear combination of A0and A1,causing that the Lie algebra generated by A0and A1is a proper Lie subalgebra of su(1,1).When A1is non-parabolic,the reduced differential equation of ν1becomes

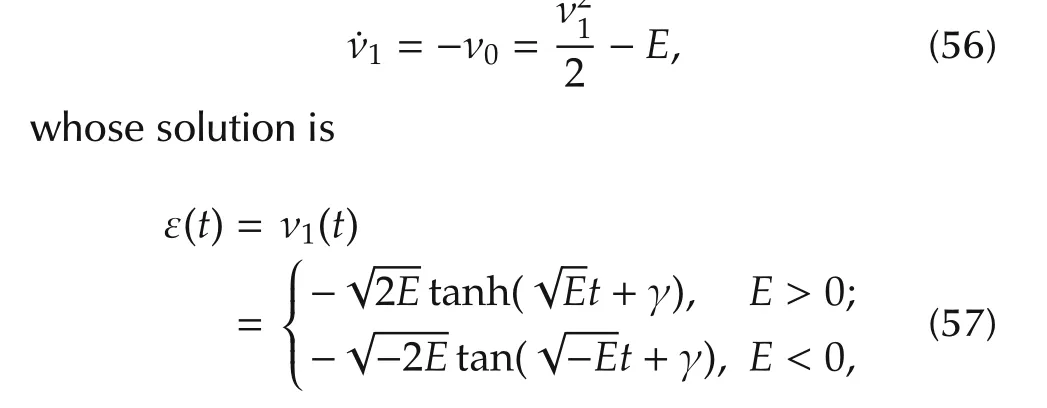
where the parameters E and γ are parameters to be determined from the boundary conditions.When A2is parabolic,the solution is simpler,i.e.,ε(t)= γe-t.

4 Optimal control of quantum squeezed states with two controls

Given a generalized SU(1,1)coherent state written as|α = θe-iφ?,the parameter ξ =tanh θe-iφcharacterizes a squeezed optical state in quantum optics.The value of|ξ|=tanhθ ∈ [0,1]represents the ratio of squeezing.For standard coherent states(e.g.,those of a harmonic oscillator),|ξ|=0,while the limit|ξ|→ 1correspondsto a highly squeezed state.In the representation(24),one can verify that ξ =x2/x1where x=[x1x2]T=R-1(|α?).

Consider the quantum system controlled by a circularly polarized field,which is mapped as in equations(26)-(28)to the following optimal control system:

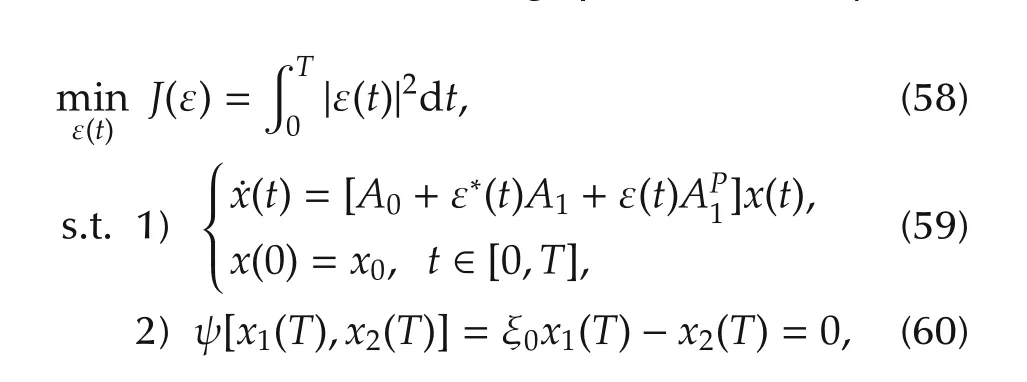
where T is not fixed.ξ0is the target squeezing ratio and(T),x2(T)]in equation(60)is the constraints of the system final state.

More specifically,we consider the often encountered case(e.g.,the two examples discussed in Section 2)that A0= ω0K0and A1=(K1+iK2)/2,where ω0is the frequency of the optical mode and the basis matrices K0,K1and K2are defined in(4).Denote ε(t)=u1(t)+iu2(t),where u1(t)and u2(t)are the real and imaginary parts of ε(t).Then we have the pseudo Hamiltonian with respect to the minimum-fluence control as

where λ0=0 or 1,and the evolution of the Lagrangian multiplier λ(t)obeys the same differential equation of x(t)because

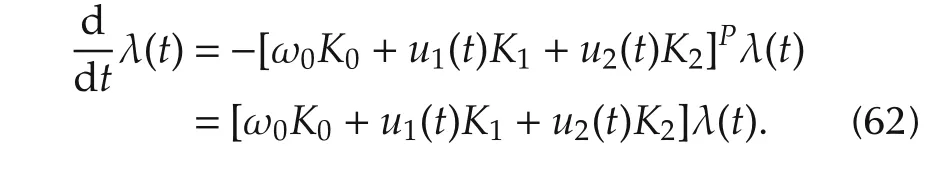
Let νi(t)=-?λ(t),Kix(t)?P,i=0,1,2.Their evolution obeys the following equations:

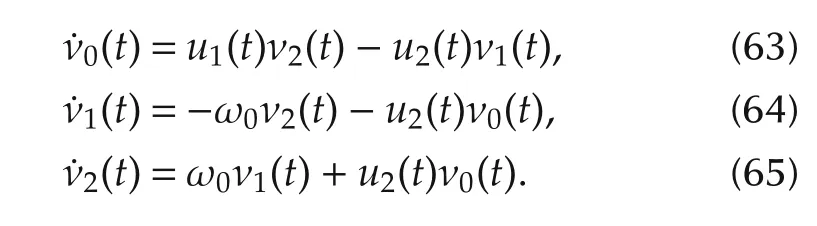
Similarly,one can prove that the abnormal extremals(i.e.,λ0=0)can only be zero control ε(t)≡ 0,which is trivial in practice.

For normal extremals(i.e.,λ0=1),the Pontryagin Maximum Principle reads

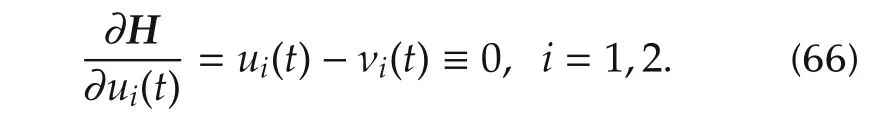
Combined with equation(63),it can be seen that

implying that ν0(t)≡ δ is constant.Thus,equations(64)and(65)become

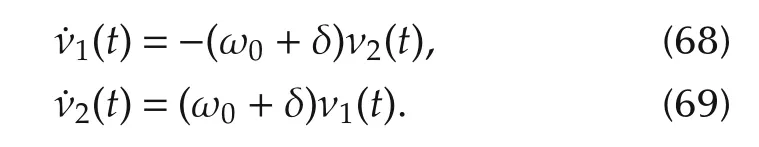
Therefore,both ν1(t)=u1(t)and ν2(t)=u2(t)are sinusoidal functions of time,where δ is the detuning frequency from the resonating frequency ω0.The resulting control field can be written as ε(t)= ν1(t)+iν2(t)=Mei[(ω0+δ)t+ψ].M and ψ can be determined from the boundary conditions

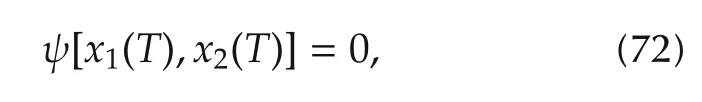
and the final time pseudo Hamiltonian condition H(T)=0.

The Sch¨odinger equation(24)under such sinusoidal control functions is analytically solvable.Using the rotating-frame transformation¯x(t)=,which leads to

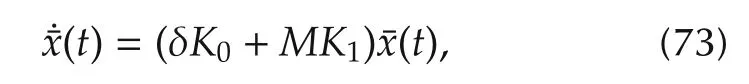
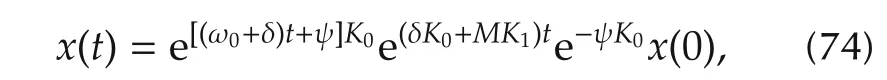
where t∈[0,T]and x(0)=(1,0)?is the vacuum state.Therefore,for a normal extremal,the field fluence isand the corresponding squeezing parameter can be computed as

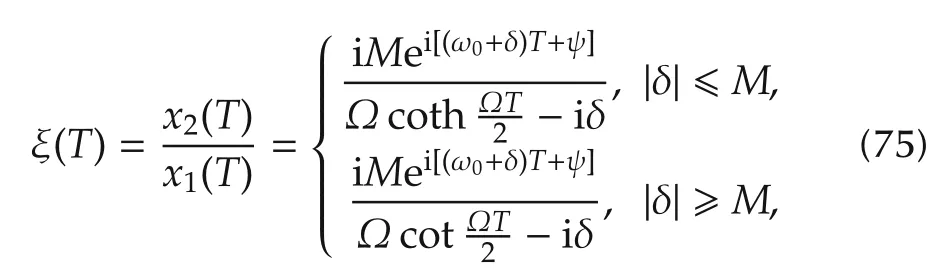
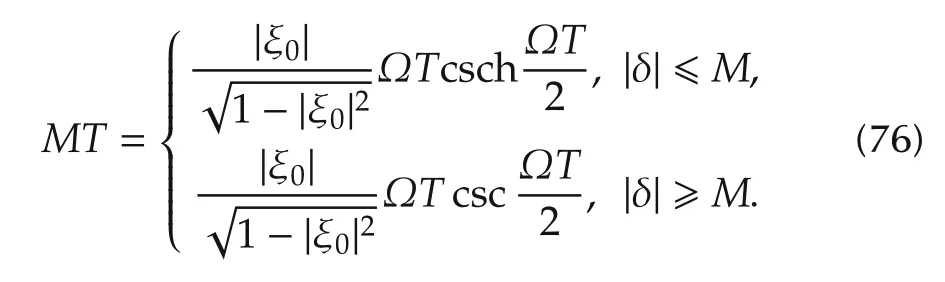
The dependence of M on the detuning parameter δ is depicted in Fig.1,where the minimum value of the field amplitude(for fixed final time T)can be seen to be reached at δ=0(i.e.,on resonance),where

or equivalently,

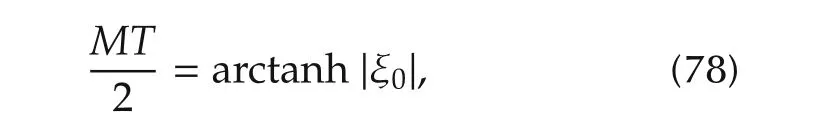
corresponding to

The phase parameter ψ can be determined by matching the phase of ξ0,i.e.,

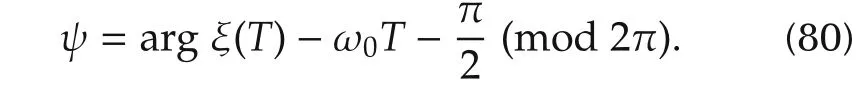
Fig.1 The minimal amplitude M of the control field required for state squeezing at the ratio of ξ0under various detuning frequency δ,where T is the final time.The required field becomes stronger when the detuning is greater or the final state is more squeezed.

From the above derivation, one can also solve the dual problem of maximizing the squeezing ratio ξ(T)under given control fluence F=.Note that the restrictionon the fluence implies that M=

From the above results,the state can be squeezed with a higher degree when increasing the quantity FT,which can be done by either increasing the fluence of the field or extending the time of interaction of the pump field with the medium.

5 Conclusions

The optimal control for quantum system has obtained many fruitful results[37,38].In this paper,we used the optimal control method to study the minimum-fluence control of quantum generalized coherent states in systems with SU(1,1)dynamical symmetry.It was found that,according to the geometry of the system control Hamiltonian(i.e.,its parabolicity),the optimal control solutions with a single control field can be expressed in terms of Weierstrass elliptic functions.Different from the related work on the group SU(2)[19],the properties of extremal controls are much more complicated due to the noncompactness of SU(1,1)group.For systems with two controls,we proved that the optimal control is a monochromatic field that is resonant with the frequency of the mode to be controlled,which is exactly what is used in laboratory from physical intuition.These results reflect the complexity in controlling unbounded quantum systems even on a finite dimensional submanifold.In the future,the optimal control theory will be applied to quantum systems with more general dynamical symmetries.We will also make use of optimal control theory to study other issues,e.g.,the decoherence problems[39,40]inopenSU(1,1)dynamicalsymmetry.

[1] C.Lan,T.-J.Tarn,Q.-S.Chi,et al.Analytic controllability of timedependent quantum control systems.Journal of Mathematical Physics,2005,46(5):DOI 10.1063/1.1867979.

[2]M.Berrondo,A.Palma.Group theory of the morse potential.Group Theoretical Methods in Physics.Berlin:Springer,1980:3-7.

[3]F.El-Orany,S.Hassan,M.Abdalla.Squeezing evolution with non-dissipative SU(1,1)systems.Journal of Optics B:Quantum and Semiclassical Optics,2003,5(5):396-404.

[4]S.-H.Dong,F.Lara-Rosano,G.-H.Sun.The controllability of the pure states for the Morse potential with a dynamical group SU(1,1).Physics Letters A,2004,325(3):218-225.

[5]R.P.Mart’ınez-y-Romero,H.N.N’u˜nez-Y’epez,A.L.Salas-Brito.An su(1,1)algebraic method for the hydrogen atom.Journal of Physics A:Mathematical and General,2005,38(40):8579-8588.

[6]A.Thilagam,M.A.Lohe.Coherent state polarons in quantum wells.Physica E,2005,25(4):625-635.

[7]K.W’odkiewicz,J.H.Eberly.Coherentstates,squeezed fluctuations,and the SU(2)and SU(1,1)groups in quantumoptics applications.Journal of the Optical Society of America B:Optical Physics,1985,2(3):458-466.

[8]Y.Alhassid,F.G¨ursey,F.Iachello.Group theory approach to scattering.Annals of Physics,1983,148(2):346-380.

[9]Y.Dothan.Finite-dimensional spectrum-generating algebras.Physical Review D,1970,2(12):2944-2954.

[10]J.Dukelsky,G.G.Dussel,C.Esebbag,et al.Exactly solvable models for atom-molecule hamiltonians.Physical Review Letters,2004,93(5):DOI 10.1103/PhysRevLett.93.050403.

[11]I.Buluta,S.Ashhab,F.Nori.Natural and artificial atoms for quantum computation.Reports on Progress in Physics,2011,74(10):DOI 10.1088/0034-4885/74/10/104401.

[12]C.M.Caves.Quantum-mechanical noise in an interferometer.Physical Review D,1981,23(8):1693-1708.

[13]A.F.Pace,M.J.Collett,D.F.Walls.Quantum limits in interferometric detection of gravitational radiation.Physical Review A,1993,47(4):3173-3189.

[14]C.Brif,R.Chakrabarti,H.Rabitz.Control of quantum phenomena:Past,present,and future.New Journal of Physics,2010,12(7):DOI 10.1088/1367-2630/12/7/075008075008.

[15]Z.Shaterzadeh-Yazdi,P.S.Turner,B.C.Sanders.SU(1,1)symmetry of multi mode squeezed states.Journal of Physics A:Mathematical and Theoretical,2008,41(5):DOI 10.1088/1751-8113/41/5/055309.

[16]R.Wu,R.Chakrabarti,H.Rabitz.Optimal control theory for continuous variable quantum gates.Physical Review A,2008,77(5):DOI 10.1103/PhysRevA.77.052303.

[17]D.Dong,I.Petersen.Quantum control theory and applications:a survey.IET Control Theoryamp;Applications,2010,4(12):2651-2671.

[18]A. P. Peirce, M. A. Dahleh, H. Rabitz. Optimal control of quantum-mechanical systems:Existence,numerical approximation,and applications.Physical Review A,1988,37(12):4950-4964.

[19]D.D’Alessandro,M.Dahleh.Optimal control of two-level quantum systems.IEEE Transactions on Automatic Control,2001,46(6):866-876.

[20]V.Jurdjevic.Non-Euclidean elastica.American Journal of Mathematics,1995,117(1):93-124.

[21]V.Jurdjevic.Hamiltonian point of view of non-Euclidean geometry and elliptic functions.Systemsamp;Control Letters,2001,43(1):25-41.

[22]U.Boscain,G.Charlot,J.-P.Gauthier,et al.Optimal control in laser-induced population transfer for two-and three-level quantum systems.Journal of Mathematical Physics,2002,43(5):2107-2132.

[23]Y.Sachkov.Conjugate points in euler’s elastic problem.Journal of Dynamical and Control Systems,2008,14(3):409-439.

[24]Y. Sachkov. Control theory on Lie groups. Journal of Mathematical Sciences, 2009, 156(3): 381 - 439.

[25]J.Wu,C.Li,R.Wu,et al.Quantum control by decomposition of SU(1,1).Journal of Physics A:Mathematical and General,2006,39(43):13531-13551.

[26]N.Ja.Vilenkin,A.U.Klimyk.Representation of Lie Groups and Special Functions.Boston:Kluwer Academic Publishers,1991.

[27]A.M.Perelomov.Coherent states for arbitrary Lie group.Communications in Mathematical Physics,1972,26(3):222-236.

[28]T.-J. Tarn, G. Huang, J. W. Clark. Modelling of quantum mechanical control systems. Mathematical Modelling, 1980, 1(1):109 - 121.

[29]R.Wu,T.-J.Tarn,C.Li.Smooth controllability of infinite-dimensional quantum-mechanical systems.Physical Review A,2006,73(1):DOI 10.1103/PhysRevA.73.012719.

[30]C. Brif, A. Mann. Nonclassical interferometry with intelligent light.Physical Review A, 1996, 54(5): 4505 - 4518.

[31]C.Brif.SU(2)and SU(1,1)algebra eigenstates:a unified analytic approach to coherent and intelligent states.International Journal of Theoretical Physics,1997,36(7):1651-1682.

[32]A.B.Klimov,S.M.Chumakov.A Group-theoretical Approach to Quantum Optics:Models of Atom-field Interactions.Weinheim:John Wileyamp;Sons,2009.

[33]S.Banks,M.Yew.On the optimal control of bilinear systems and its relation to Lie algebras.International Journal of Control,1986,43(3):891-900.

[34]J.Baillieul.Geometric methods for nonlinear optimal control problems.Journal of Optimization Theory and Applications,1978,25(4):519-548.

[35]V.Jurdjevic.Geometric Control Theory.New York:Cambridge University Press,1997.

[36]D.F.Lawden.Elliptic Functions and Applications.New York:Springer,1989.

[37]S.C.Hou,M.A.Khan,X.X.Yi,et al.Optimal lyapunov-based quantum control for quantum systems.Physical Review A,2012,86(2):DOI 10.1103/PhysRevA.86.022321.

[38]W.Zhou,S.G.Schirmer,M.Zhang,et al.Bang-bang control design for quantum state transfer based on hyperspherical coordinates and optimal time-energy control.Journal of PhysicsA:Mathematical and Theoretical,2011,44(10):DOI 10.1088/1751-8113/44/10/105303.

[39]W.Cui,Z.Xi,Y.Pan.Optimal decoherence control in non-markovian open dissipative quantum systems.Physical Review A,2008,77(3):DOI 10.1103/PhysRevA.77.032117.

[40]J.Zhang,C.Li,R.Wu,et al.Maximal suppression of decoherence in markovian quantum systems.Journal of Physics A:Mathematical and General,2005,38(29):6587-6601.

26 September 2014;revised 6 May 2015;accepted 7 May 2015

†Corresponding author.

E-mail:rbwu@tsinghua.edu.cn.Tel.:+86-10-62797485;fax:+86-10-62786911.

This work was supported by the National Natural Science Foundation of China(Nos.61374091,61134008).

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg

Wenbin DONG was born in Shenyang,China.He received his B.Sc.and M.Sc.degrees from Northeastern University,Shenyang,China,in2008and2010,respectively.Currently,he is a Ph.D.candidate at the Tsinghua University,Beijing.His main research interests are quantum control.E-mail:dongwenbin77@163.com.

Rebing WU received the B.Sc.degree in Electrical Engineering,and the Ph.D.degree in Control Science and Engineering from Tsinghua University,Beijing,China,in 1998 and 2004,respectively.From 2005 to 2008,he was a Research Associate Fellow with the Department of Chemistry,Princeton University,Princeton,NJ.Since 2009,he has been an Associate Professor with the Department of Automation,Tsinghua University,Beijing,China.His research interests include quantum mechanical control theory and nonlinear control theory.E-mail:rbwu@tsinghua.edu.cn.

Jianwu WU was born in Zhejiang,China.He received his B.Sc.degree from Beihang University(BUAA)in2003,and received his Ph.D.degree from Tsinghua University,Beijing,in 2008.His main research interest is quantum control.Currently,he is working in Beijing Aerospace Automatic Control Institute.E-mail:wujw03@mails.tsinghua.edu.cn.

Chunwen LI received the B.Sc.and Ph.D.degrees from the Department of Automation,Tsinghua University,Beijing,China,in 1982and1989,respectively.Since1994,he has been a Professor with the Department of Automation,Tsinghua University.His research interests include nonlinear control systems,inverse systems,CAD and simulation of nonlinear systems,and robust control.Dr.Li received the National Youth Prize in 1991 and the Prize of the Chinese Outstanding Ph.D.Degree Recipient in 1992.E-mail:lcw@tsinghua.edu.cn.

Tzyh-Jong TARN received the D.Sc degree in Control System Engineering from Washington University,St.Louis,MO.He is a Professor in the Department of Systems Science and Mathematics and the Director of the Center for Robotics and Automation,Washington University.Dr.Tarn received the Best Research Article Award from The Japan Foundation for the Promotion of Advanced Automation Technology in March 1994 and the Best Paper Award at the 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems.He has served as the President of the IEEE Robotics and Automation Society(1992-1993).He currently serves as the Chairman of the Nomination Committee of the Robotics and Automation Society,a member of the IEEE TABRAB Transnational Committee,the Editor of the IEEE TABPress Book Series on Design and Applications,the Director of IEEE Division X(Systems and Control),and is a member of the IEEE Board of Directors.E-mail:tarn@seas.wustl.edu.