Error quantification of the normalized right graph symbol for an errors-in-variables system

Lihui GENG,Shigang CUI,Zeyu XIA

Tianjin Key Laboratory of Information Sensing and Intelligent Control,School of Automation and Electrical Engineering,

Tianjin University of Technology and Education,Tianjin 300222,China

Error quantification of the normalized right graph symbol for an errors-in-variables system

Lihui GENG†,Shigang CUI,Zeyu XIA

Tianjin Key Laboratory of Information Sensing and Intelligent Control,School of Automation and Electrical Engineering,

Tianjin University of Technology and Education,Tianjin 300222,China

This paper proposes a novel method to quantify the error of a nominal normalized right graph symbol(NRGS)for an errorsin-variables(EIV)system corrupted with bounded noise.Following an identification framework for estimation of a perturbation model set,a worst-case v-gap error bound for the estimated nominal NRGS can be first determined from a priori and a posteriori information on the underlying EIV system.Then,an NRGS perturbation model set can be derived from a close relation between the v-gap metric of two models and H∞-norm of their NRGSs’difference.The obtained NRGS perturbation model set paves the way for robust controller design using an H∞loop-shaping method because it is a standard form of the well-known NCF(normalized coprime factor)perturbation model set.Finally,a numerical simulation is used to demonstrate the effectiveness of the proposed identification method.

Error quantification,errors-in-variables,normalized right graph symbol

DOI10.1007/s11768-015-4183-6

1 Introduction

Normalized coprime factors(NCFs)with their respective additive perturbations play an important role in the robust control area since McFarlane and Glover[1,2]presented a robust controller design method using NCF plant descriptions via open-loop shaping.A nominal NCF model can not only characterize possible unstable systems,but also reduce fragility in the robust controller design[3].As a result,such robust controller synthesis method using NCF representations attracts more and more attention in the subsequent years.As for an underlying system characterized by a NCF perturbation model set,various methods capable of synthesizing robustly stabilizing controllers are presented[4-13].For the purpose of achieving robust controller design,the available nominal model should be a NCF representation for the concerned system.Even more importantly,a worst-case error bound for the NCF perturbations should also be determined before the controller design.As a result,identification of a NCF perturbation model set for the concerned system is a particularly significant stage prior to its robust controller synthesis.Although quite a few estimation methods are able to provide users with a nominal NCF model,few of them can also give its worst-case error bound necessary to design a robust controller[14,15].This is due to the reason that such a specific mathematical description makes it difficult to quantify a worst-case error for the obtained nominal NCF model.Therefore,it is of particular necessity to study quantification methods for the NCF perturbations.

The major contribution of this paper is to propose a novel error quantification method,which can provide users with a kind of NCF perturbation model set suitable to robust controller design.In order to retain our research continuity,we also name it as normalized right graph symbol(NRGS)perturbation model set.The idea of the proposed error quantification method derives from some previous researches,in which Geng et al.put forward an identification method for obtaining a perturbation model set characterized by the v-gap metric.In a matter of fact,the v-gap metric describes a deterministic geometrical relation between the NRGSs of two concerned systems and thus is much related to the error quantification of the nominal NRGS addressed in this paper.In an identification framework similar to those in[16]and[17],a much less conservative error bound for nominal NRGS perturbations can be derived from the determined v-gap metric bound.The resultant NRGS perturbation model set can thus be represented as the nominal NRGS and its worst-case error bound.In addition,the identified model set has the same form as the NCF perturbation model set[18,19]and thus is beneficial to the subsequent application of an H∞loopshaping design method.

The remainder of this paper is organized as follows.Section 2 formulates an errors-in-variables system framework for identification of an NRGS perturbation model set.A deterministic relation between the NRGS perturbation bound and the v-gap perturbation bound and thus a worst-case error for the nominal NRGS are both derived in Section 3.In addition,an identification procedure to obtain such NRGS perturbation model set is also summarized.Section 4 gives a simulation example to demonstrate how to apply the proposed identification procedure.Some concluding remarks about the proposed identification method are drawn in Section 5.

The notations in this paper are standard[16,17,19-21].Let Rm×ndenote the set of m × n real matrices and let C stand for the set of complex numbers.L2(D),H∞(D)and H2(D)are the subspaces of specified functions in the Hardy space.¯σ(X)symbolizes the maximum singular value of a complex matrix X.l∞denotes the space of bounded sequences.A ball in l∞is defined as:={v:v∈and δv(P1,P2)are the L2-gap and the v-gap metric between P1(λ)and P2(λ),respectively[21].X∗denotes the complex conjugate of a complex matrix X.

2 Problem formulation

We only consider robust identification of an NRGS model for a SISO errors-in-variables(EIV)system shown in Fig.1,which describes the following signal relation

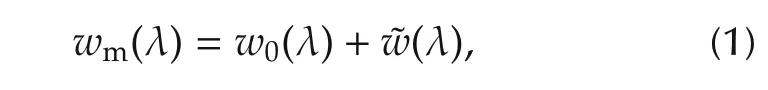
where wm(λ)≜ [ym(λ)um(λ)]Tis the input and output measurement variable vector,w0(λ) ≜ [y0(λ)u0(λ)]Tthe noise-free input and output variable vector,and ˜w(λ)≜[ny0(λ)nu0(λ)]Tthe input and output disturbing noise variable vector.In the block diagram,P0(λ)∈ H∞(D)is an open-loop discrete-time system,whose NRGS is G0(λ)=[N0(λ)D0(λ)]T∈ H∞(D)[16,17,20,21].

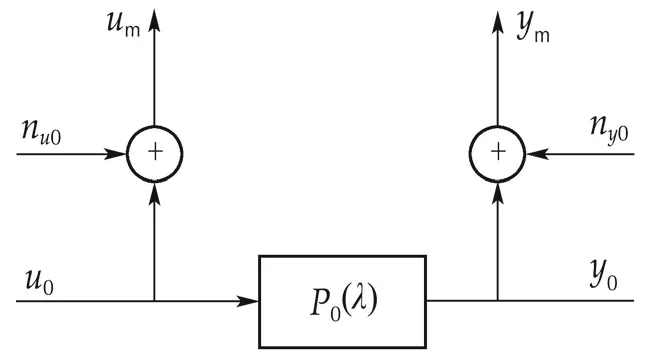
Fig.1 Block diagram of an EIV system.

For the purpose of the EIV system identification,the following necessary assumptions are given.

Assumption 1wm(λ)and˜w(λ)belong to L2(D).

Assumption 2The disturbing noise˜w(λ)belongs to the following noise set

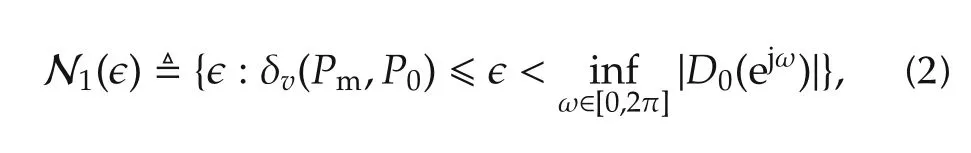
where Pm(λ)=ym(λ)/um(λ)is a perturbed model resulting from˜w(λ).

Assumption 1 is a more general condition for openloop EIV system identification[16,17,22].From As-sumption 2,a Pm(λ)belonging to H∞(D)can be ensured to exist[17].Moreover,an NRGS of Pm(λ)can be described as Gm(λ)=[Nm(λ)Dm(λ)]T∈ H∞(D).

We make use of Gm(λ)to define a a priori model set for the NRGS G0(λ)of the underlying EIV system P0(λ)as follows[16,17]:

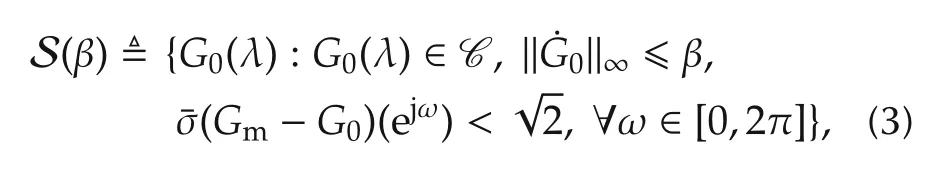
where C denotes the space of functions with continuous derivatives on the unit circle∂D and˙G0means a derivative of G0(λ)with respect to the complex variable λ.

Remark1 The model set S(β)ofG0(λ)definedin(3)is one whose element derivative is continuous and constrained to be less than the a priori bound β. In effect, any G0(λ)contained in this model set needs to have some certain smoothness and thus its components N0(λ)and D0(λ)should also have the similar property.

However,in an identification experiment,only a finite number of input and output measurement sequences,k ∈ N ≜ {1,2,...,N}}are available.Suppose that the angular frequencies,collected from[0,2π]as a set W ≜ {ω1,ω2,...,ωN},are nonuniform samples which satisfy

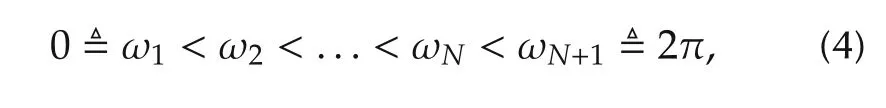
where ωN+1is an artificial angular frequency not used for identification.Then,the maximum frequency gap between adjacent angular frequencies can be determined as

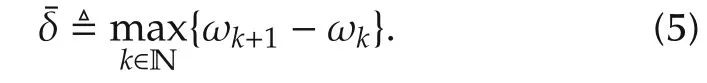
To sum up,our main objective is to estimate an(n-1)th order nominal NRGS G(λ)of an approximate model P(λ)for P0(λ)using the recorded data setin the first place and then quantify its worst-case error in terms of a priori and a posteriori information on the underlying EIV system.

3 Worst-case identification

3.1 Optimization criterion

By the same token,the identification method proposed in[17]is employed here to obtain the nominal NRGS G(λ).To this end,a coprime factor model F(λ)=[NF(λ)DF(λ)]T∈ H∞(D)of P(λ)should be first optimized from the following optimization criterion[16,17,21]:

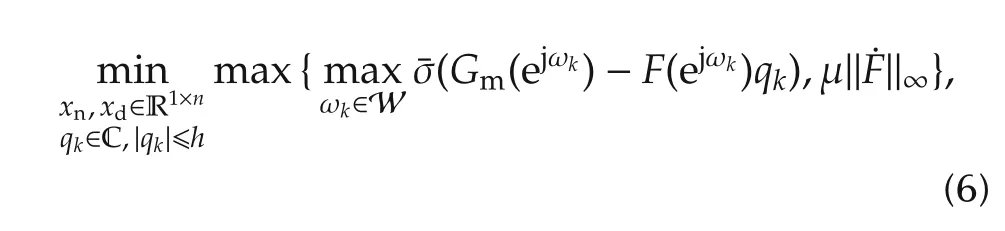
where Gm(ejωk)is the point wise frequency response of Gm(λ)and can be generated from the input and output measurements as follows:

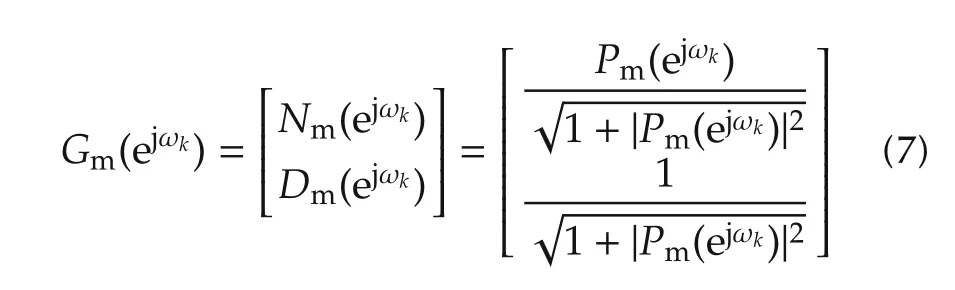
with Pm(ejωk)=ym(ejωk)/um(ejωk)for ωk∈ W;F(ejωk)is the pointwise frequency response of the following parametric coprime factor model

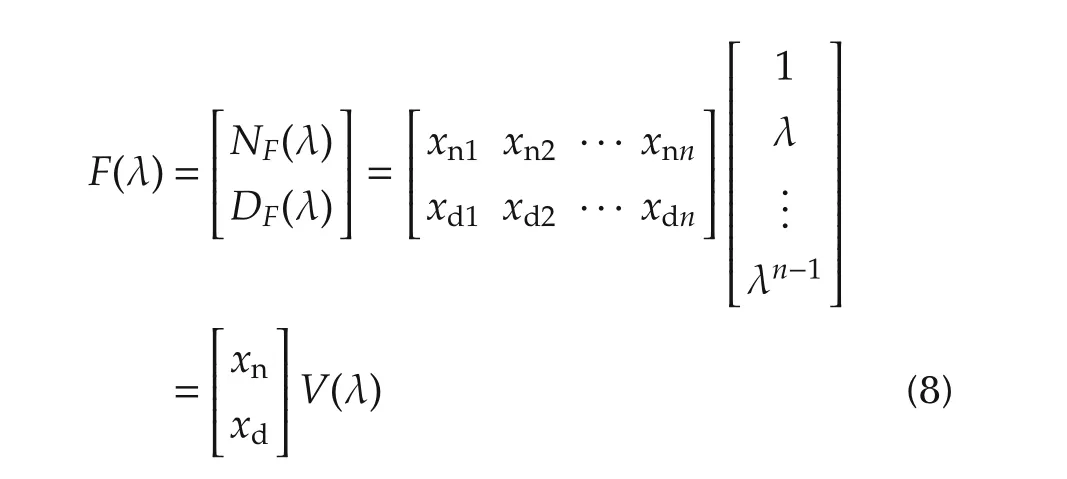
with

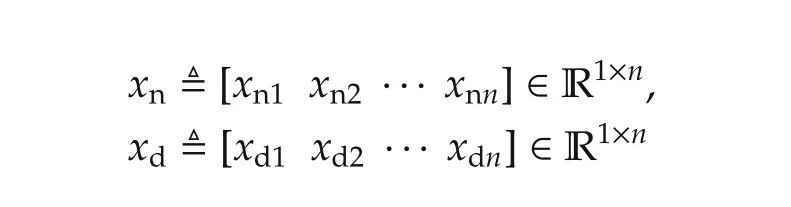
being the parameters for the numerator and denominator factors,respectively and V(λ)=[1 λ ···λn-1]T∈a set of orthonormal basis for linear dynamical models;qkis a complex variable to be optimized at ωk;μ is a user-chosen weighting coefficient for H∞-norm of the derivative of F(λ)with respect to λ.

Remark 2 In minimization criterion(6),not only the aperture betweenbut also the smoothness of F(λ)is minimized and this minimization problem can be solved by a two-step iterative algorithm[20].The complex variable qkis bounded by h,which can be determined as a posteriori information from q=at the end of the two-step iterative algorithm.The weighting coefficient μ can be chosen asμ˜δ¯rwithμ˜∈(0,∞)and r∈(0.5,1)from[20].

Then,an estimation of G(λ)can be obtained as=by applying a normalization procedure toPˆ(λ)≜withNˆF(λ)andDˆF(λ)being the optimized models from(6).

3.2 Worst-case error quantification

According to a priori and a posteriori information on the underlying EIV system,a worst-case error forˆG(λ)is defined as

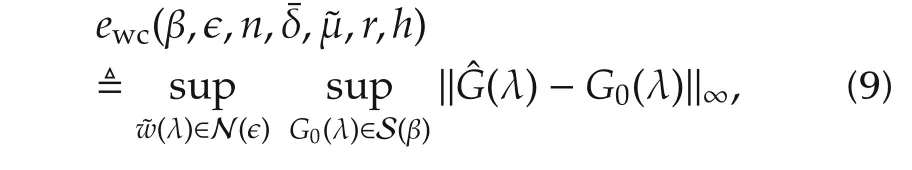
1N2(?)and N3(?)are defined as follows:

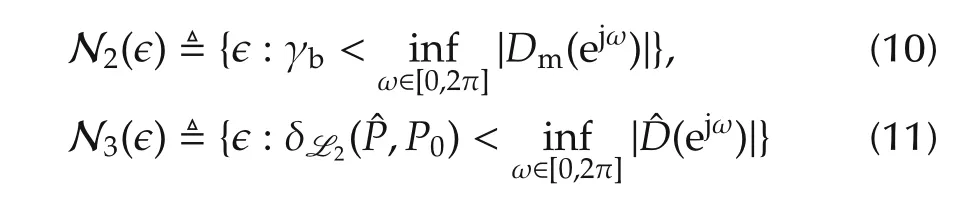
with γbbeing a possible upper bound for the optimal value of optimization criterion(6)andˆD(ejω)being the frequency response of the denominator factor inˆG(λ).It is noteworthy that N2(?)and N3(?)are used to further constrain the noise bound?and will be beneficial for the quantification of a worst-case error bound for ewc.In addition,the constraint inequality in N3(?)is a sufficient condition for the existence of δv(ˆP,P0)[17],which will be later used in a robust convergent theorem.

In order to quantify the worst-case error ewc,the following pivotal theorem ought to be addressed in advance.

Theorem 1If the v-gap metric δv(ˆP,P0)between ˆP(λ)and P0(λ)exists andˆG(λ)and G0(λ)are their respective NRGSs,then the following inequality holds:

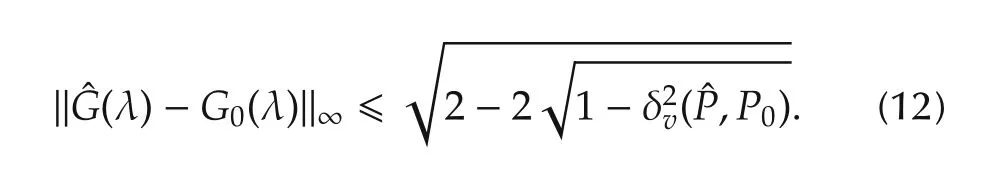
Proof This theorem can be readily concluded from the statements in Appendix A in[16]and further consideration of the existence of δv(ˆP,P0).□

From Theorem 1,a useful corollary can be obtained in a straightforward manner.

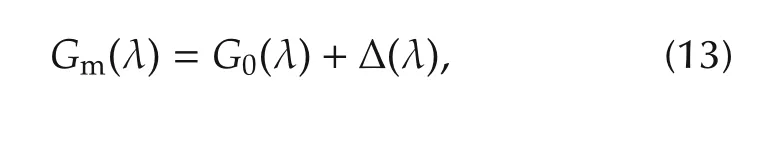
Corollary1 The following NRGS perturbation model can be derived:where Δ(λ) ≜ [Δn(λ) Δd(λ)]T∈ H∞(D)is the numerator and denominator perturbations for G0(λ)and can be determined.

In order to quantify the worst-case error in(9)and prove the relevant robust convergence of the employed identification algorithm,we recall the following lemma[17,21].

Lemma 1 For the a priori informationW}∈S(β)and the a posteriori information as in(7),there exist two(n-1)th order polynomialssuch that the following inequalities hold

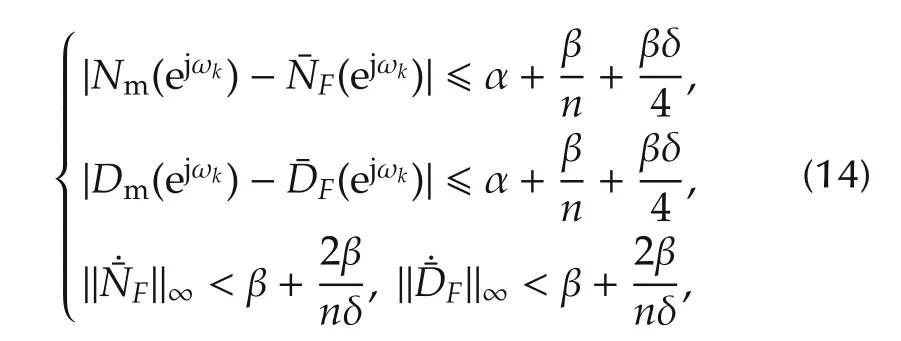
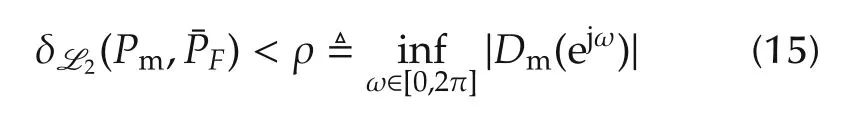
and

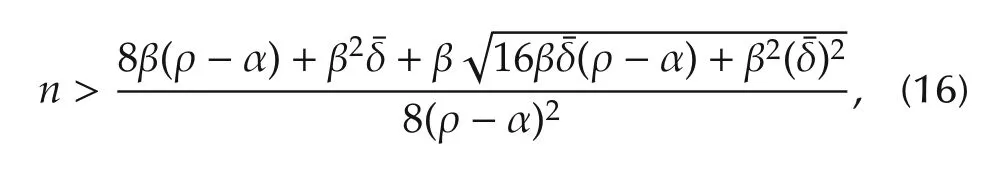
which are used to ensure the coprimeness between¯NF(λ)and¯DF(λ)[17].

Remark3 The constraint condition in(15)is applied to ensure the existence of a δv(Pm,¯PF),which is helpful in the quantification of δv(ˆP,P0).Inequality(16)is used to guarantee that¯NF(λ)and¯DF(λ)are coprime in H∞(D).In a matter of fact,a sufficient large n can be determined to make(15)and(16)hold simultaneously(See Remark 3 in[16]).

Similar to the proof of the robust convergent Theorem3.4 in[17],the following important lemma can thus be obtained.

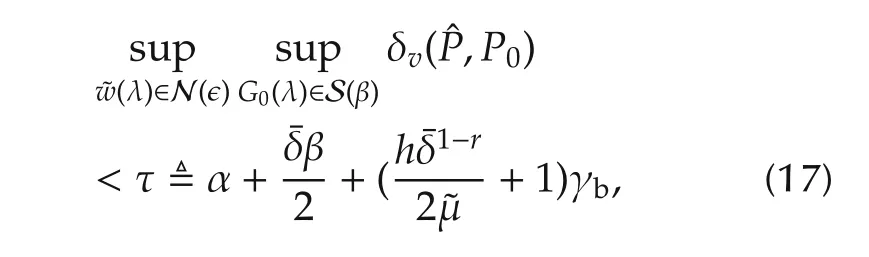
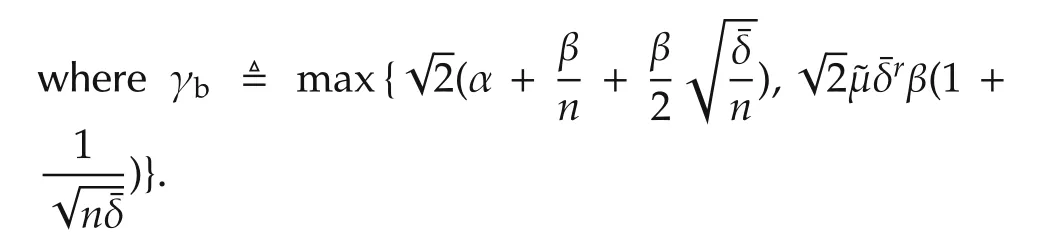
In light of Lemma 2,one is able to derive a robust convergent theorem as follows.

Theorem 2 Under the same condition as in Lemma 2,the worst-case error forˆG(λ)can then be quantified as

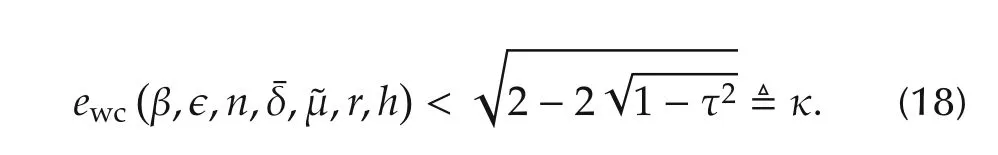
In addition,

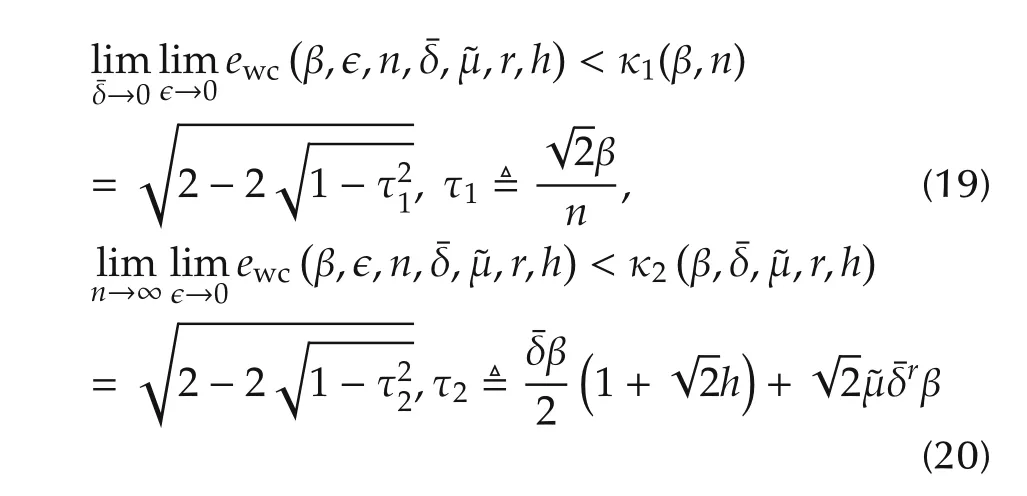
with

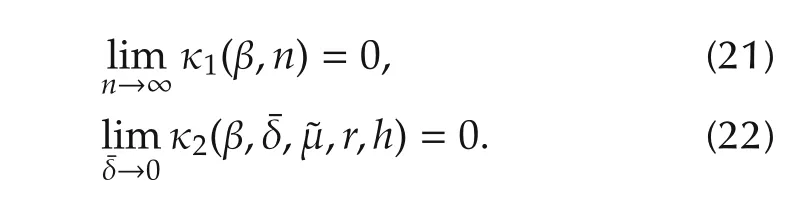
Proof Combining Theorem 1 and Lemma 2 yields the relevant conclusions for this theorem. □

From Theorem 2,it can be known that the proposed algorithm has robust convergence and the worst-case error for the nominal NRGSˆG(λ)can be quantified according to(18).

3.3 Identification procedure

The identification of an NRGS perturbation model set for an EIV system using frequency-domain measurements can be summarized as the following steps.

Step 1 Generate the point wise frequency responseaccording to the input and output measurements

Step 2 Build the point wise frequency responseofbased on equation(7).

Step 3 Parameterize the coprime factor model F(λ)by referring to equation(8).

Step 4 Optimize an(n-1)th order coprime factor modelˆF(λ)from the optimization criterion in(6)and then normalize it asˆG(λ)by means of the relevant procedure addressed in[19].

Step 5 Quantify the worst-case error ewcdefined in(9)by use of Theorem 2 with a priori and a posteriori information on the underlying EIV system.

Remark 4 The identified NRGS perturbation model set is characterized by a nominal NRGS and its wors-tcase error bound. Also, this model set has the same form as that of the NCF perturbation model set addressed in[2].Thus,the H∞loop-shaping controller synthesis method therein can be used to design a robust controller for the estimated NRGS perturbation model set.The detailed study on a robustly stabilizing controller tailored to the model set given in this paper will be discussed elsewhere.

4 Simulation

In this section,the proposed worst-case identification method is tested on a SISO EIV system, in which the true system can be described by the following discrete-time transfer function of a complex variable z[17]:

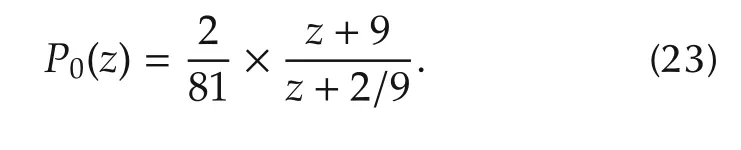
In an identification experiment,the frequency response of P0(z)is corrupted by a zero-mean Gaussian measurement noise whose variance is frequency-dependent and taken as the following form

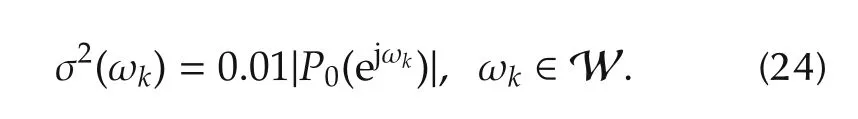
Frequency-response measurements with the data length N=80 are collected from an angular frequency interval[0.001,π-0.001]for identification.In the above simulation environment,the maximum frequency gap is computed as

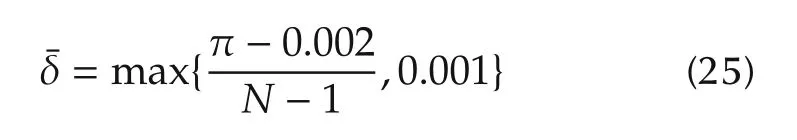
and a priori bound?is 0.0978.By simple computation,Assumption 2 holds since?is less than0.9692.By use of inequality constraint(16),the model order n can be chosen as 4.The a priori information on β is 0.3453.During the minimization of optimization criterion(6),the following selection for the weighting coefficient μ can be determined as[20]

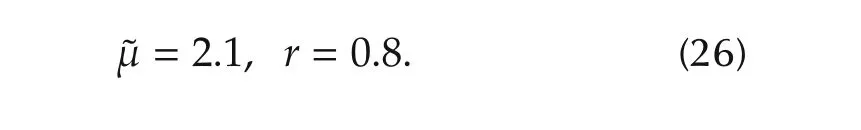
After the implementation of the proposed identification procedure,the optimal solution forˆF(λ)is obtained as

Meanwhile,the corresponding optimal value can be calculated as γopt=0.0847.Then an estimated nominal NRGSˆG(λ)can be normalized as

The estimated denominator and nominator factors are compared with their respective true ones in Figs.2 and 3.A comparison between the estimated and the true system models is also given in Fig.4.The worst-case error bound for the identified NRGS model can be determined as κ=0.4383.

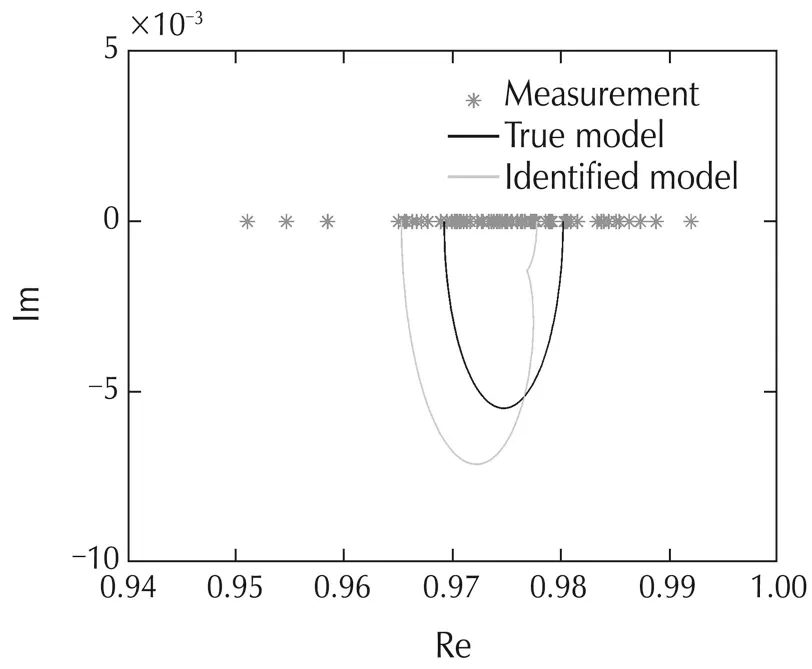
Fig.2 Comparison of denominator factors.

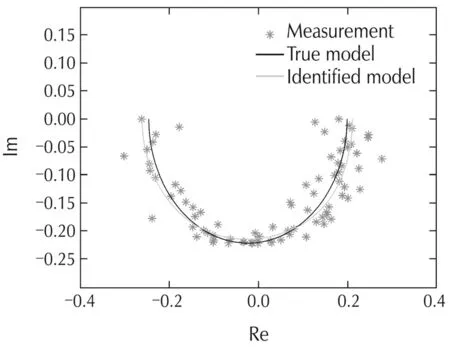
Fig.3 Comparison of numerator factors.

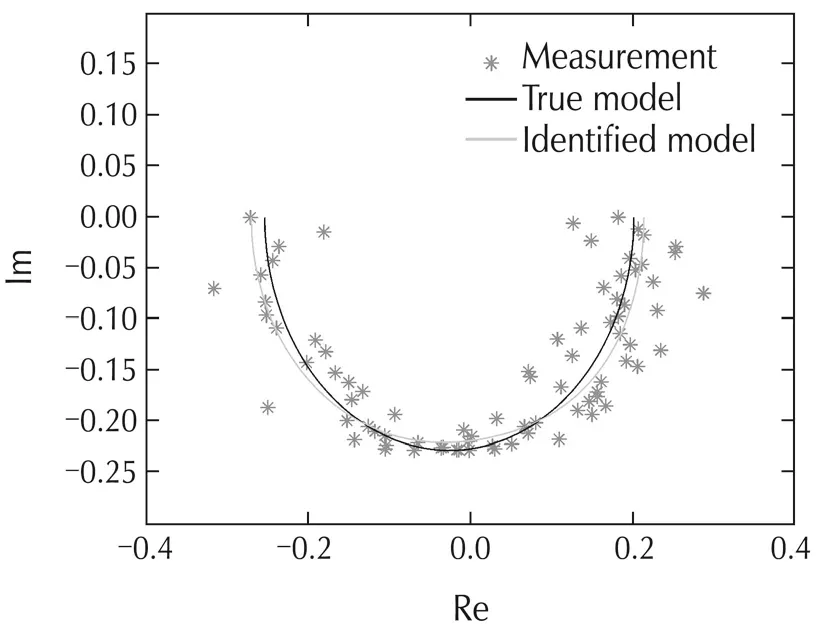
Fig.4 Comparison of system models.

Hence,an NRGS perturbation model set for the underlying EIV system P0(z)can be represented as the nominal modelˆG(λ)and its worst-case error bound κ,which pave the way for its H∞controller design.

5 Conclusions

It is a thorny problem to quantify a worst-case error for the NCF perturbations using a priori and a posteriori information on an underlying system.By exploitation of a geometrical interpretation of the v-gap metric,a novel quantification method for the worst-case error of an NRGS model for an EIV system is proposed in this paper.The obtained NRGS perturbation model set consisting of a nominal NRGS and its worst-case error bound is tailored to an H∞loop-shaping controller design method.

[1]K.Glover,D.C.McFarlane.Robust stabilization of normalized coprime factor plant descriptions with H∞-bounded uncertainty.IEEE Transactions on Automatic Control,1989,34(8):821-830.

[2]D.C.McFarlane,K.Glover.Robust Controller Design Using Normalized Coprime Factor Plant Descriptions.Lecture Notes in Control and Information Sciences.Heidelberg:Springer,1990.

[3]J.Paattilammi,P.M.Makila.Fragility and robustness:a case study on paper machine head box control.IEEE Control Systems Magazine,2000,20(1):13-22.

[4]P.P.Khargonekar.Maximally robust state-feedback controllers for stabilization of plants with normalized right coprime factor uncertainty.Systemsamp;Control Letters,1994,22(1):1-4.

[5]R.Majumder,B.C.Pal,C.Dufour,et al.Design and real-time implementation of robust FACTS controller for damping interarea oscillation.IEEE Transactions on Power Systems,2006,21(2):809-816.

[6]T.Oomen,O.Bosgra.Robust-control-relevant coprime factor identification:a numerically reliable frequency domain approach.Proceedings of the American Control Conference,Seattle:IEEE,2008:625-631.

[7]J.C.Oostveen,R.F.Curtain.Robustly stabilizing controllers for dissipative infinite-dimensional systems with collocated actuators and sensors. Automatica,2000,36(3):337-348.

[8]S.Patra,S.Sen,G.Ray.Design of static H∞loop shaping controllerin four-block framework using LMI approach.Automatica,2008,44(8):2214-2220.

[9]J.Reinschke,M.C.Smith.Designing robustly stabilising controllers for LTI spatially distributed systems using coprime factor synthesis.Automatica,2003,39(2):193-203.

[10]J.F.Whidborne,I.Postlethwaite,D.-W.Gu.Robust controller design using H∞loop-shaping and the method of inequalities.IEEE Transactions on Control Systems Technology,1994,2(4):455-461.

[11]K.K.Anaparthi,B.C.Pal,H.El-Zobaidi.Coprime factorisation approach in designing multi-input stabiliser for damping electromechanical oscillations in power systems.IEE Proceedings-Generation,Transmission and Distribution,2005,152(3):301-308.

[12]B.D.O.Anderson,M.R.James,D.J.N.Limebeer.Robust stabilization of nonlinear systems via normalized coprime factor representations.Automatica,1998,34(12):1593-1599.

[13]R.F.Curtain.Robustly stabilizing controllers with respect to left-coprime factor perturbations for infinite-dimensional linear systems.Systemsamp;Control Letters,2006,55(7):509-517.

[14]M.R.Graham,R.A.de Callafon.Linear regression method for estimation approximate normalized coprime plant factors.Proceedings of the 14th IFAC Symposium on System Identification.Newcastle,Australia:IFAC,2006.

[15]P.M.J.Van den H of,R.J.P.Schrama,O.H.Bosgra,et al.Identification of normalized coprime plant factors for iterative model and controller enhancement.Proceedings of the 32nd IEEE Conference on Decision and Control.San Antonio:IEEE,1993:2839-2844.

[16]L.Geng,D.Xiao,T.Zhang,et al.Worst-case identification of errors-in-variables models in closed loop.IEEE Transactions on Automatic Control,2011,56(4):762-771.

[17]L.Geng,D.Xiao,T.Zhang,et al.Robust control oriented identification of errors-in-variables models based on normalised coprime factors.International Journal of Systems Science,2012,43(9):1741-1752.

[18]M.Vidyasagar.ControlSystem Synthesis:A Factorization Approach.Cambridge,MA:MIT Press,2002:261-262.

[19]K.Zhou,J.C.Doyle,K.Glover.Robust and Optimal Control.Upper Saddle River:Prentice-Hall,1996.

[20]P.Date,G.Vinnicombe.An algorithm for identification in the vgap metric.Proceedings of the 38th IEEE Conference on Decision and Control.Phoenix,Arizona:IEEE,1999:3230-3235.

[21]P.Date,G.Vinnicombe.Algorithms for worst case identification in H∞and in the v-gap metric.Automatica,2004,40(6):995-1002.

[22]L.Geng,D.Xiao,T.Zhang,et al.L2-optimal identification of errors-in-variables models based on normalised coprime factors.IET Control Theory and Applications,2011,5(11):1235-1242.

[23]M.Glaum,L.Lin,G.Zames.Optimal H∞approximation by systems of prescribed order using frequency response data.Proceedings of the 35th IEEE Conference on Decision and Control.Kobe,Japan:IEEE,1996.

24 December 2014;revised 10 July 2015;accepted 13 July 2015

†Corresponding author.

E-mail:glh2010@tute.edu.cn.

This work was supported in part by the National Natural Science Foundation of China(Nos.61203119,61304153),the Key Program of Tianjin Natural Science Foundation,China(No.14JCZDJC36300)and the Tianjin University of Technology and Education funded project(No.RC14-48).©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg

Lihui GENG received the B.E.,the M.E.and the Ph.D.degrees from Tianjin University of Commerce,Hebei University of Technology and Tsinghua University in 2000,2003 and 2011,respectively.Currently,he is an associate professor at the School of Automation and Electrical Engineering,Tianjin University of Technology and Education.His research interests include system identification and its engineering applications.E-mail:glh2010@tute.edu.cn.

Shigang CUI received the M.E.and the Ph.D.degrees both from Tianjin University in 1991 and 2004,respectively.Currently,he is a professor at the School of Automation and Electrical Engineering,Tianjin University of Technology and Education.In addition to being a director of this school,he has also served as a director of Tianjin Key Laboratoryof Information Sensing and Intelligent Control.His research interests cover robot control and applications.E-mail:cuisg@163.com.

Zeyu XIA received the B.E.degree from the Department of Computer Engineering,Anhui Economic Management Cadres’Institute in 2007.Currently,he is pursuing the M.E.degree at the School of Automation and Electrical Engineering,Tianjin University of Technology and Education.His research interests include system identification and its engineering applications.E-mail:798364309@qq.com.