Quasi-Newton-type optimized iterative learning control for discrete linear time invariant systems

Yan GENG,Xiaoe RUAN

School of Mathematics and Statistics,Xi’an Jiaotong University,Xi’an Shaanxi 710049,China

Quasi-Newton-type optimized iterative learning control for discrete linear time invariant systems

Yan GENG,Xiaoe RUAN†

School of Mathematics and Statistics,Xi’an Jiaotong University,Xi’an Shaanxi 710049,China

In this paper,a quasi-Newton-type optimized iterative learning control(ILC)algorithm is investigated for a class of discrete linear time-invariant systems.The proposed learning algorithm is to update the learning gain matrix by a quasi-Newton-type matrix instead of the inversion of the plant.By means of the mathematical inductive method,the monotone convergence of the proposed algorithm is analyzed,which shows that the tracking error monotonously converges to zero after a finite number of iterations.Compared with the existing optimized ILC algorithms,due to the super linear convergence of quasi-Newton method,the proposed learning law operates with a faster convergent rate and is robust to the ill-condition of the system model,and thus owns a wide range of applications.Numerical simulations demonstrate the validity and effectiveness.

Iterative learning control,optimization,quasi-Newton method,inverse plant

1 Introduction

Iterative learning control(ILC)has been acknowledged as one of the effective techniques that achieves perfect trajectory tracking while the system implements the tracking task repetitively over a fixed time-interval,see,e.g.,[1-6].Arimoto et al.[1]firstly introduced ILC as an intelligent teaching mechanism called“betterment process”for robot manipulators.Numerous ILC contributions have come forth over the past three decades scoping from theoretical investigations to practical applications.As one of the important theoretical issues,the convergence analysis has been discussed by Amann et al.[2],Xu[3],and Meng et al.(2-D analysis approach)[5]and Ruan et al.[6,7].In addition,the robustness has been discussed from many aspects,such as stochastic noise in[8],iteration-varying disturbances in[9],model uncertainty in[10]and time-delay uncertainty in[11],etc.,stability and initial state learning have been researched in[12]and[13],respectively.Another significant contribution to ILC theory is optimal ILC algorithms in articles[14-19].In terms of the applications of ILC, the categories mainly include robotics in[20],rotary systems in[21],chemical batch processing in[22],etc.Ahn et al.[23]provided a summary and review of the recent trends in ILC research from both the application and the theoretical aspects.

In optimization field,it is known that the gradient method,the conjugate direction method,the Newton method as well as the quasi-Newton method have been acknowledged as effective optimization techniques for their widely applications in the areas of industry,agriculture,military and medical treatment,see,e.g.,[24-26].Guided by the practicability and the validity of the optimization techniques,a number of investigations have been made which focus on embedding some of the above-mentioned optimization methods into the ILC algorithms[14-19].Referring to the scheme of optimization technique,the mode of such an optimized ILC up-dating law is to generate a sequence of optimized control inputs by minimizing performance index function.

In this aspect,Amann et al.[2]firstly introduced the concept of optimal ILC algorithm for linear systems based on optimization theory and made a comprehensive analysis of norm-optimal ILC(NOILC).After that,Owens and Feng[15]proposed a parameter optimization ILC(POILC)for discrete linear time-invariant systems and derived its monotone convergence under the assumption that the system satisfies a positivity condition.Besides,Owens et al.[16]offered a gradient-type ILC algorithm and analyzed its convergence in a rigorous manner.The analogous work was to establish an inverse model ILC scheme named as a Newton-type ILC algorithm,and made a comprehensive analysis in term of the convergence and the robustness as shown in[17].It is noticed that the optimized ILC strategies in[15-17]are model-based,of which both the necessity and the sufficiency of the monotone convergence are involved.

Theoretically,it is thus no doubt that the inverse model ILC scheme owns a one-step terminative performance for the case when the inversion of the model of the plant is precisely identified in prior and well conditioned.In reality,on the one hand,the inverse model algorithm is quite sensitive to the perturbation incurred by some measurement noise or slow changing of the system parameters.On the other hand,the inverse model technique may not work for the model imprecision.This implies that the inverse model ILC is hardly realizable in practical executions.In order to avoid the complexities of matrix inversion,Owens et al.[18]developed a polynomial approximation ILC(PAILC)algorithm which replaces the inverse model of the plant by a polynomial.However,the ILC algorithm requires plenty of computation to capture the inversions of the system matrices and thus is just implementable to a lower dimensional plant or a less operational processing.Besides,as the searching directory of the gradient type ILC mechanism,article[16]prevailed to a saw path with a very small learning step when the iteration-wise approximate optimum is close to the desired one,the convergent rate of the gradient-type ILC is to some extent not satisfactory,especially when the system is ill conditioned.In 2013,Yang and Ruan[19]developed a type of conjugate direction ILC scheme for linear discrete time-invariant systems to speed up the convergent rate.

In spite of the above-mentioned executable limitation,the inverse mode ILC mechanism remains referable to develop an efficient learning law.As such,a quasi-Newton-type ILC updating law is a candidate,which adopts an approximate matrix to replace the inverse model of the plant.This motivates the paper to developa quasi-Newton-type ILC strategy for discrete linear time invariant systems and derives its convergence as well.

The paper is organized as follows.Section2 presents two types of quasi-Newton ILC schemes abbreviated as SR1-ILC algorithm and SR2-ILC algorithm,respectively.Section3 exhibits the monotonic convergence.Numerical simulations are illustrated in Section4 and the conclusions are drawn in Section5.

2 Quasi-Newton-type optimized ILC algorithm

Consider a class of repetitive discrete linear time invariant single-input-single-output(SISO)systems described as follows:

where t∈I represents the sampling time with I={0,1,...,N}denoting the set of the sampling times and N standing for the total number of the sampling times,respectively.Thevariablesx(t)∈Rn,u(t)∈Rand y(t)∈R are respectively an n-dimensional state vector,a scalar input and a scalar output at the sampling time t.A,B and C are matrices with appropriate dimensions,respectively,satisfying CB≠0.The model system(1)is reformulated in a lifted input-output form as follows:

where

It is obvious that G is an invertible Markov para meters based transfer matrix.

Let yd=[yd(1)yd(2) ···yd(N)]Tbe a given desired trajectory of system(2)and e=yd-y=[yd(1)-y(1)yd(2)-y(2) ···yd(N)-y(N)]T=yd-Gu denotes the tracking error of system(2).The ILC algorithm is to design a sequence of inputs{uk+1}so that it may drive system(2)to track the desired trajectory ydas precisely as possible as the iteration index approaches infinity.That is to say,

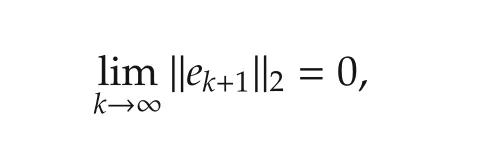
where

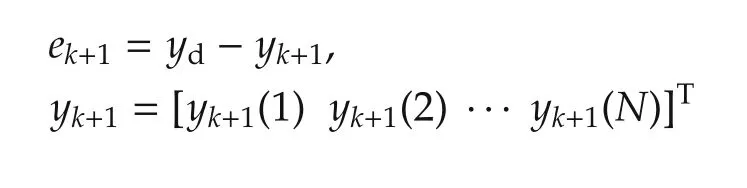
refers to the output of system(2)driven by uk+1=[uk+1(0)uk+1(1) ···uk+1(N-1)]T.Such an ILC sequence uk+1can be produced by solving an optimization problem for system(2)as follows:

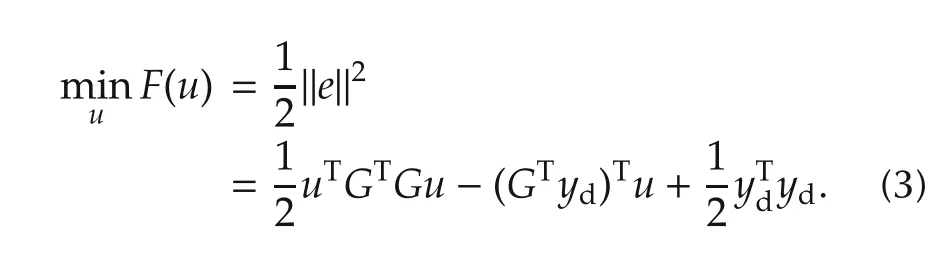
Recall that the Newton-type ILC updating law of the optimization(3)developed in article[17]takes a form of

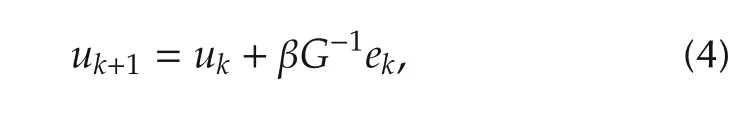
where k=1,2,...is the iterative number.ek=yd-ykis the tracking error between the desired trajectory ydand the output yk,and β is termed as a learning step length.

Obviously,the above Newton-type ILC is an inversion-model scheme,which requires amounts of computation for inversion and is usually fit for a well conditioned system.

For the purpose of avoiding the computational complexity of matrix inversion and enriching the fitness of the system mode,a feasible manner is to replace the learning gain matrix G-1of the scheme(4)by a matrix with less computation or generally conditioned. As such,an iteration-relevant matrix HkGTis adopted for the substitution and the corresponding ILC scheme named as the quasi-Newton-type optimized ILC algorithm is as follows:

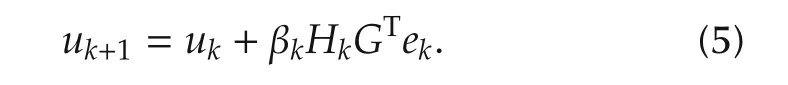
Here,Hkis the kth approximation of(GTG)-1and is updated in accordance with the quasi-Newton condition.βkis termed as the kth learning step length that obtained by exact linear search method.

The quasi-Newton ILC algorithm(5)is specified as follows.

u1and H1are given arbitrarily,

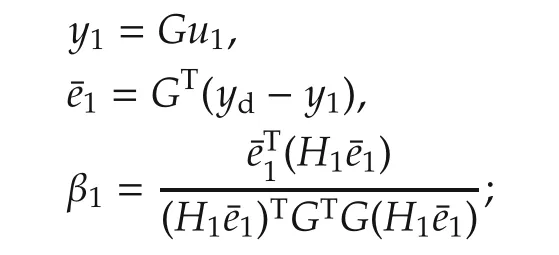
when k≥1,

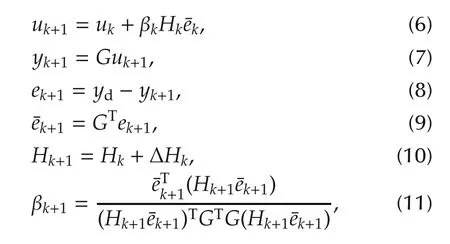
where ΔHkis a correction term which can be constructed in various forms so that the matrix Hk+1satisfies the quasi-Newton condition

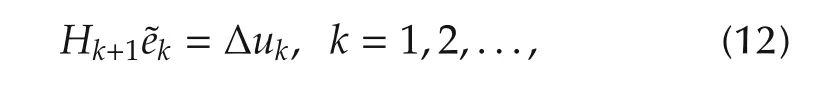
where

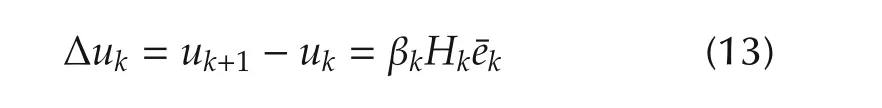
is assigned as the searching direction and

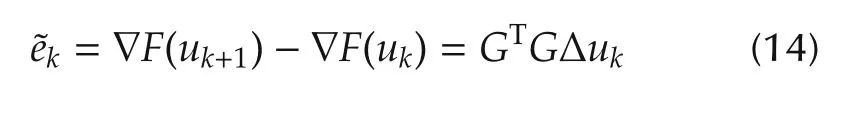
is termed as the gradient difference vector and the expression(12)is called as a secant equation.

Two typical correction forms are symmetrical-rank-1 and symmetrical-rank-2 expressed as follows:

I)Symmetrical-Rank-1(SR1)correction formula is

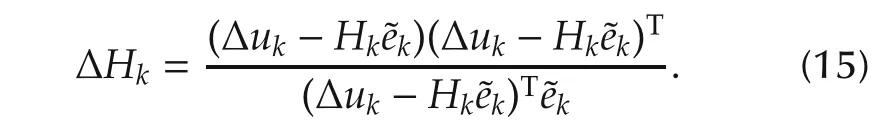
The above(6)-(11)together with the SR1 correction form(15)compose an SR1-ILC algorithm.

II)Symmetrical-Rank-2(SR2)correction formula is

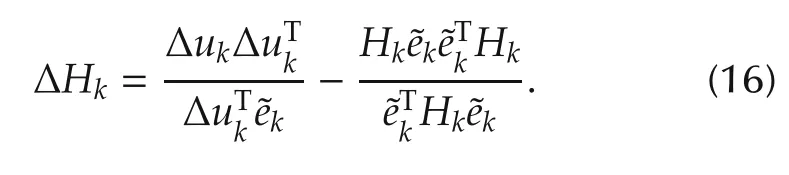
The symmetric-rank-2 form is induced by DFP correction in[27].The above(6)-(11)plus the correction form(16)is called an SR2-ILC algorithm.

3 Convergence analysis

The monotonicity of the tracking error and the termination at the finite iteration of the quasi-Newton-type optimized ILC algorithm can be concluded in the following theorem.In order to derive convergence property,some properties of the searching directions are exhibited as Lemmas 1-3 as follows.

Lemma 1 Suppose that the sequence of the gradient difference vectorsand the searching direction vectorsare generated by the SR1-ILC algorithm(6)-(11)and(15)satisfying≠0.Then,the following secant equations are true:

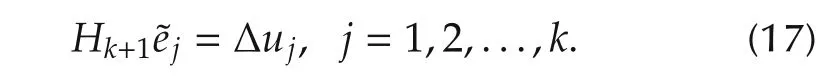
Proof Since the assumption that(Δuk+1-Hk˜ek+1)Tטek+1≠0,the SR1-ILC updating law is well-defined.The secant equations are derived by mathematical inductive method as follows.

Step 1(For the case when k=1) From the quasi-Newton condition(12),the SR1-ILC updating law satisfies the secant equation,that is,H2˜e1=Δu1is true.

Assume that the secant equations(17)are true for the the case when k=m and m=1,2,...,that is,

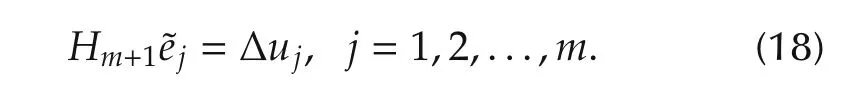
Step 2 Induce that for the case when k=m+1 the conclusion is true.

From(10)and(15),we have

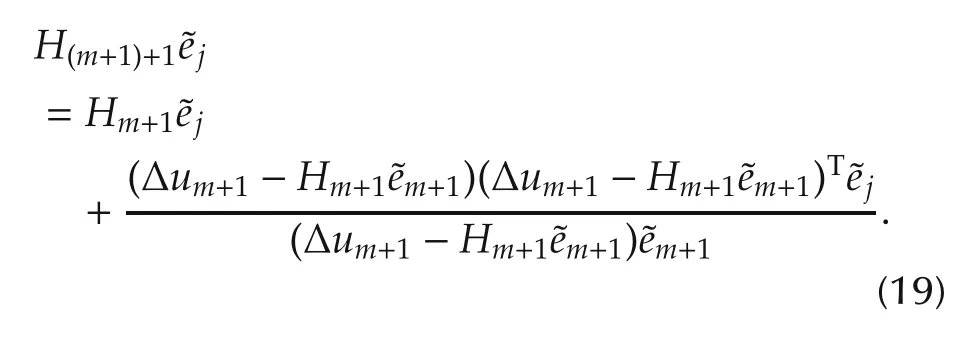
From the assumption(18),we have

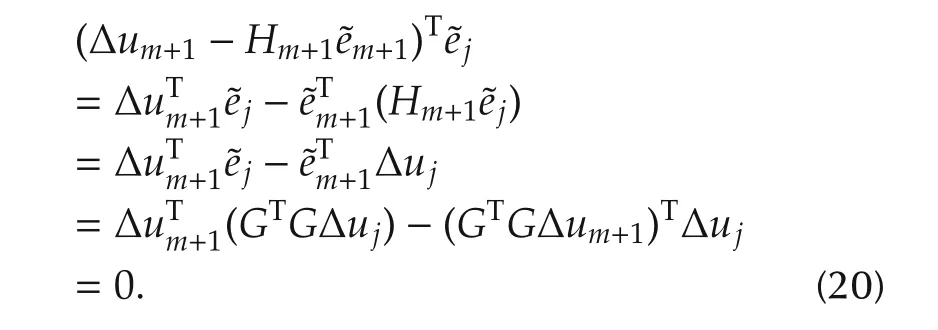
Substituting(18)and(20)into(19),we have

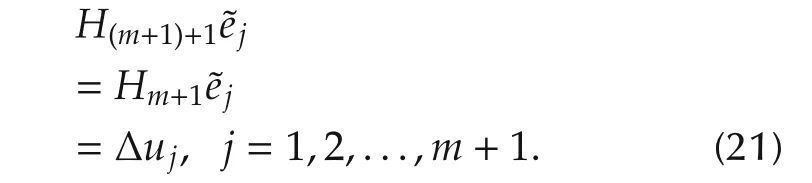
This means that(17)holds when k=m+1. □

Remark 1 From Lemma 1,it is observed that the secant equation is guaranteed to depend on not only the current tracking error but also all previous tracking errors.The SR1-ILC algorithm has the hereditary property Hk+1˜ej=Δujfor j=1,2,...,k,where Hk+1˜ej=Δujis named as the secant equation for˜ej=∇F(uj+1)-∇F(uj)and Δuj=uj+1-uj.

Lemma 2 Suppose that the searching direction vectors Δu1,Δu2,...,Δukare GTG-conjugate and k ≤ N.Then,the searching direction vectors Δu1,Δu2,...,Δukare linearly independent.

Proof Suppose that there exists such a set of numbers α1,α2,...,αkthat the equality

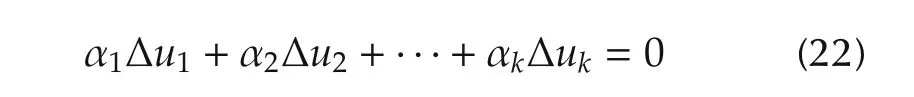
holds.Then,(22)yields

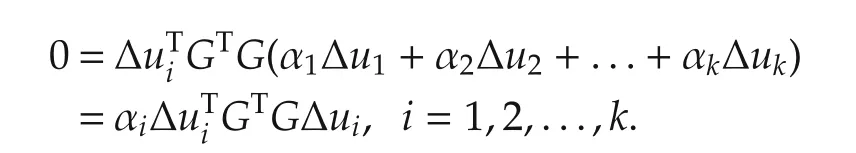
Remark 2 A set of nonzero searching direction vectors{Δu1,...,Δuk}is said to be conjugate with respect to the symmetric positive definite matrix GTG if

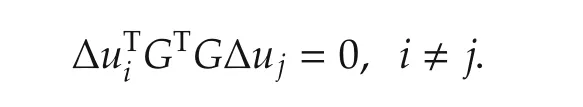
Lemma 3 Suppose that the sequence of the gradient difference vectors{˜ej}and the searching direction vectors{Δuk}are generated by SR2-ILC algorithm(6)-(11)and(16).Then,the searching direction vectors Δu1,Δu2,...,Δukare conjugate for all k ≤ N,and the following secant equations are true

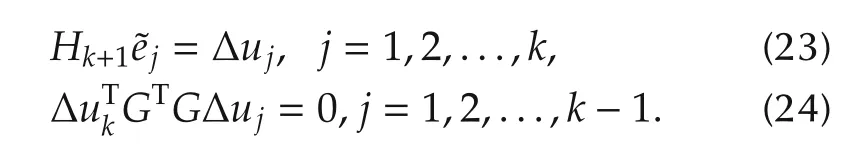
ProofBy using the mathematical inductive method,we can prove(23)and(24)to be true.

For the case when k=1,from the quasi-Newton condition(12),we have=Δu1,it shows that(23)is true.

For the case when k=2,from the property of exact line search=0,we obtain

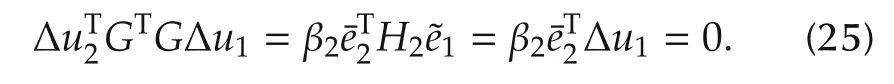
From(14)and(25),we have

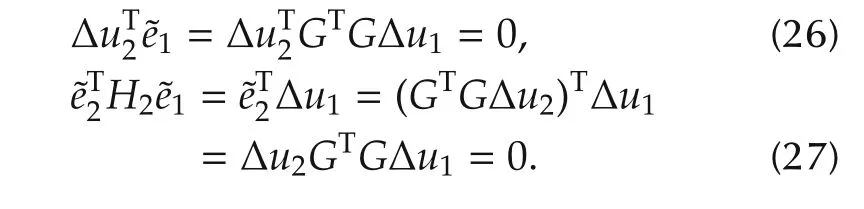
Thus,

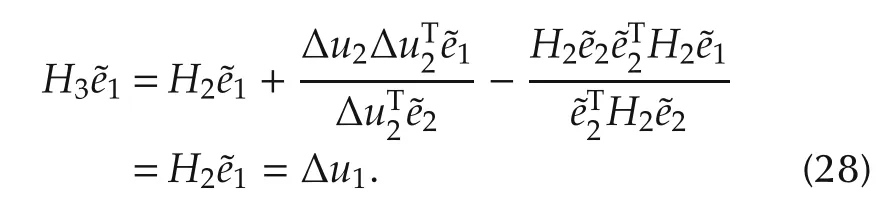
In addition,from the quasi-Newton condition(12),we have

Equalities(29)and(28)show that(23)is true and(26)shows that(24)is true for the case when k=2.

Assume that the secant equations(23)and(24)are true for the index k=m and m=1,2,...,that is

For the case k=m+1,sincee¯m+1≠0,the property of exactline search=0and inductive assumption(31)for all j≤m,we have

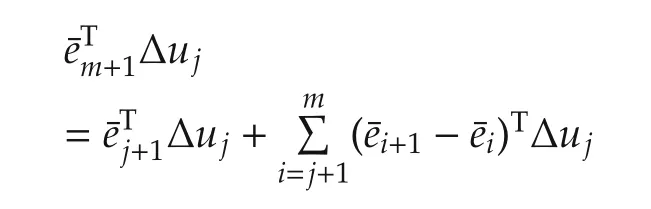
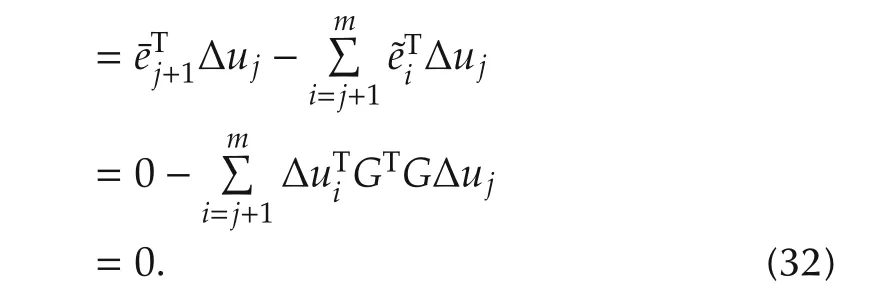
By(13),(14),(30)and(32),we have

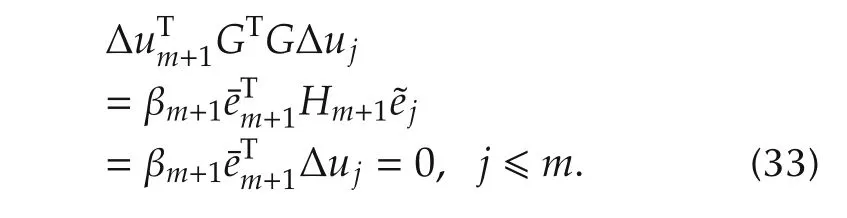
It shows that(24)holds for the case when k=m+1.

By the quasi-Newton condition,when j=m+1,we have

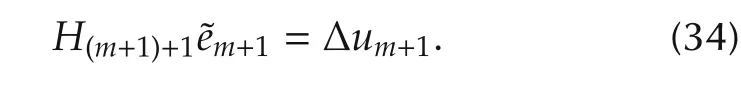
For all j≤m,from(14)and(33),we have

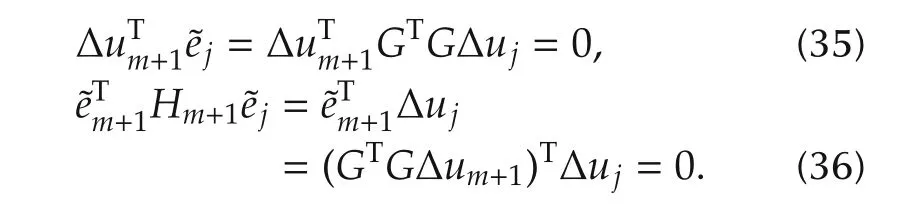
By(35)and(36),we have Expressions(34)and(37)indicate that H(m+1)+1˜ej=Δujholds,for all j=1,2,...,m+1. □

Theorem 1 Assume that the tracking errors{ek}are generated by SR1-ILC algorithm(6)-(11)and(15),then the following conclusions hold.

i)If the searching direction vectorsare linearly independent,then the tracking error ekconverges to zero at the(N+1)th iteration,which means that eN+2=0 if(N+1)th iteration is performed.

ii)If the searching direction vectors Δu1,Δu2,...,Δukare linearly dependent,Δu1,Δu2,...,Δuk-1are linearly independent,k ≤ N and(11)is replaced by βk=1,then ek+1=-∇F(uk+1)=0,which means that the input signal uk+1is the solution and the tracking error ek+1=0.

Proof From Lemma 1 we have

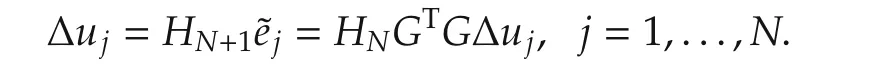
If the search direction vectors{Δuj}Nj=1are linearly inde-pendent,then HN+1GTG=I,which implies that HN+1=(GTG)-1.Thus,

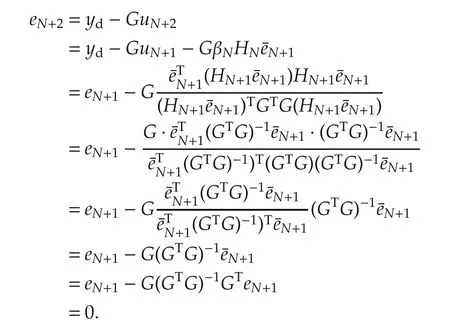
Consider the case when the searching direction vectors Δu1,Δu2,...,Δukbecome linearly dependent.Let Δukbe a linear combination of the previous iterations,we have

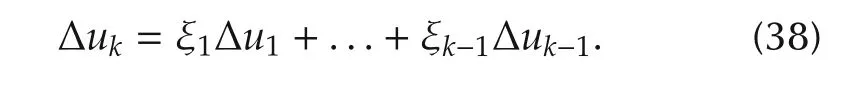
For some scalar ξi,from(14),(17)and(38)we obtain that

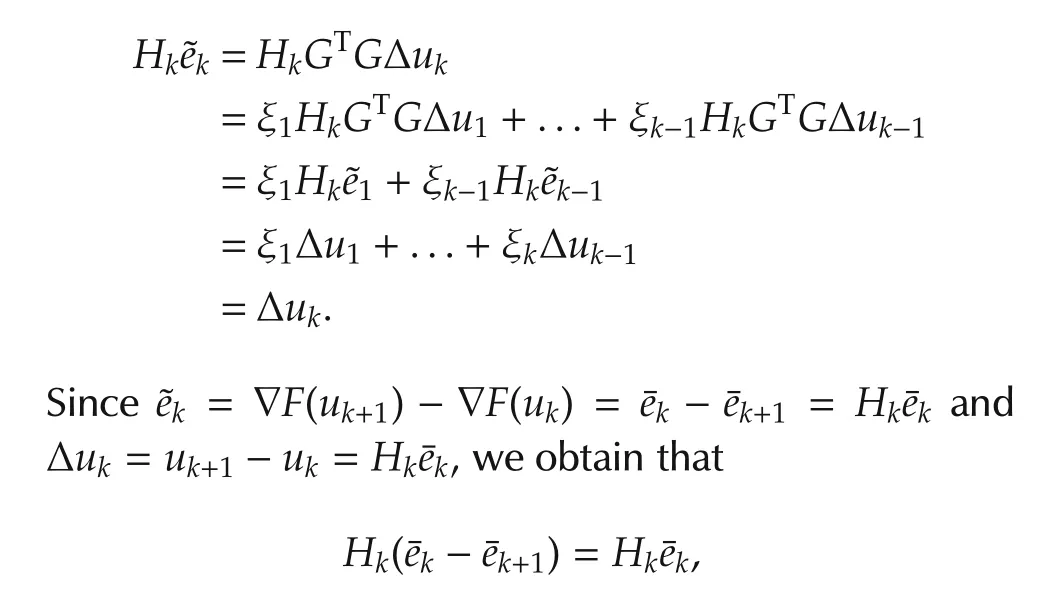
which,by then on-singularity of Hk,implies that¯ek+1=0,that is∇F(uk+1)=0.Thus,the input signal uk+1is the solution.Since¯ek+1=GTek+1=0 and G is nonsingular,then we have ek+1=0. □

Theorem 2 Assume that the tracking errors{ek}are generated by the SR2-ILC algorithm(6)-(11)and(16).Then,the tracking error ekis reduced to zero at the most(N+1)th iteration.This implies that eN+2=0 if the(N+1)th iteration is performed.

Proof If the(N+1)th iteration is performed,it follows from(24)in Lemma 3 that the vectors of search directions Δu1,Δu2,...,ΔuNare conjugate with respect to the matrix GTG.Thus,the searching direction vectors Δu1,Δu2,...,ΔuNare linearly independent by Lemma2.From(23)in Lemma 3,it yields

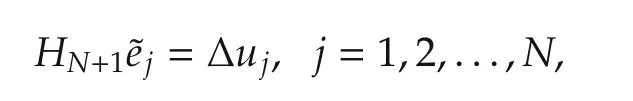
that is,

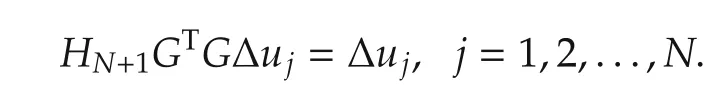
Therefore,HN+1=(GTG)-1.

Additionally,

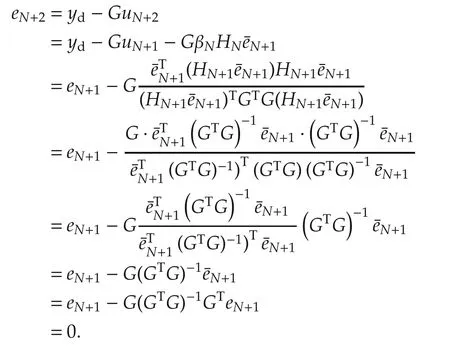
Theorem 3 Assume that the tracking errors{ek}are generated by quasi-Newton-type optimized ILC algorithm(6)-(11)for both the correction forms(15)and(16)for all k,then the norm of tracking error is monotone decreasing,that is,‖ek+1‖2≤ ‖ek‖2.

Proof

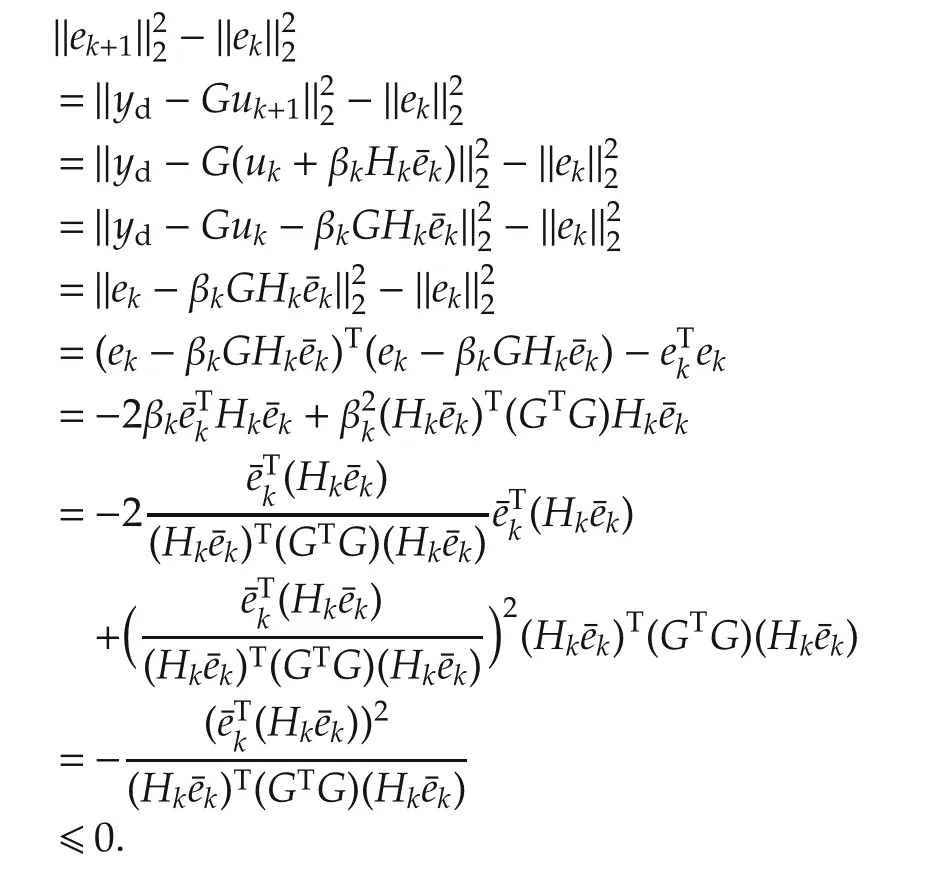
Hence,the result‖ek+1‖2≤ ‖ek‖2is proven.

Remark3 From Theorems1-3,itis clarified that the SR1(SR2)ILC has the property of quadratic termination,that is,the tracking error ekconverges monotonically to zero at the most(N+1)th iteration.While as the NOILC in[2],Gradient-ILC in[16]and PA-ILC in[18]are convergent with nonzero quotient convergence factors.This implies that the proposed quasi-Newton ILC may guarantee zero-tracking error at a finite iteration whilst the NOILCin[2],Gradient-ILC in[16]and the PA-ILCin[18]only guarantee the tracking error is at most very small.

4 Numerical simulations

In order to manifest the feasibility and practicality of the proposed SR1-ILC(SR2-ILC)scheme to a wide range of systems,this section gives simulation results for three examples,of which Example 1 is a well-conditioned system whilst Example 2 is an ill-conditioned system and Example3 is a real system.For the same initial input u1,SR1-ILC and SR2-ILC can generate the same sequence of inputs uk,the details can be referred to the articles[27]and[28].

Example 1 Consider the following discrete time invariant SISO system,which was adopted in[29].

The desired trajectory is predetermined as

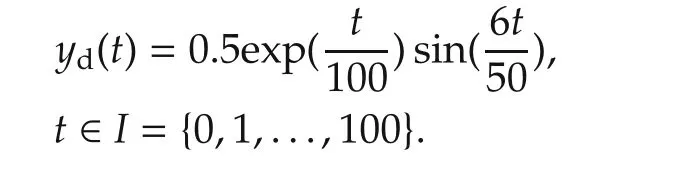
The initial state is set xk(1)=[0 0]Tand the beginning input u1(t)=0.It is calculated that the condition number of the matrix GTG is 1.6145 and the largest singular value of GTG is 0.3524.This means that the exampled system(39)is well-conditioned.

The comparative tracking errors in 2-norm of the SR1-ILC(SR2-ILC)algorithm with that of the norm optimal ILC(NOILC)[2]and gradient-based ILC(Gradient-ILC)[16]are presented in Fig.1.The tracking outputs of the SR1-ILC(SR2-ILC)at the 5th iteration and that of the NOILC and Gradient-ILC are exhibited in Fig.2.Itis seen from Figs.1 and 2 that the tracking error of the SR1-ILC(SR2-ILC)algorithm converges faster than the others.

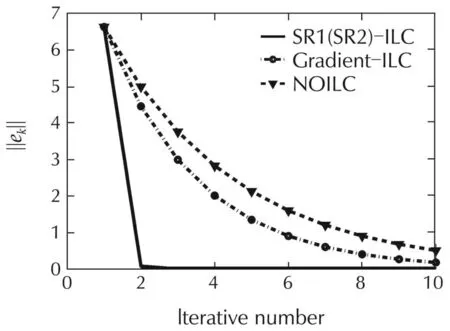
Fig.1 Tracking errors of SR1(SR2)-ILC,Gradient-ILC and NOILC.

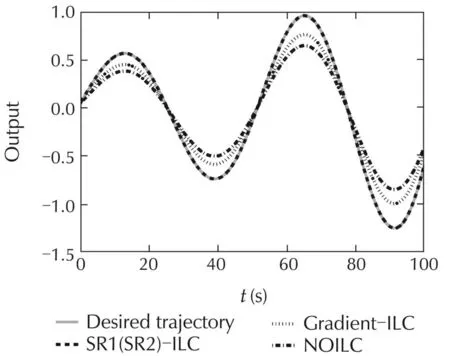
Fig.2 Tracking outputs of SR1(SR2)-ILC,Gradient-ILC and NOILC at the 5th iteration.

Example 2 Consider the following discrete timeinvariant SISO systems that was used in[30].

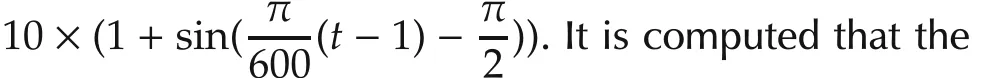
From Fig.3,it is found that the tracking error of the SR1-ILC(SR2-ILC)converges to zero at the 10th itera-tion and Fig.4 illustrates that the tracking error of the SR1-ILC(SR2-ILC)converges faster than that of NOILC algorithm.Additionally,Fig.5 gives a comparable tracking errors of natural logarithm form of2-norm ofSR1-ILC(SR2-ILC)with those produced by the PA-ILC[18]with polynomial degree being L=1,2,...,7,respectively.It shows that the convergence of tracking error of SR1-ILC(SR2-ILC)is faster than the PA-ILC after the 15th iteration.As system(40)is extremely ill-conditioned,its convergent assumption with respect to the Gradient-ILC algorithm is not guaranteed.

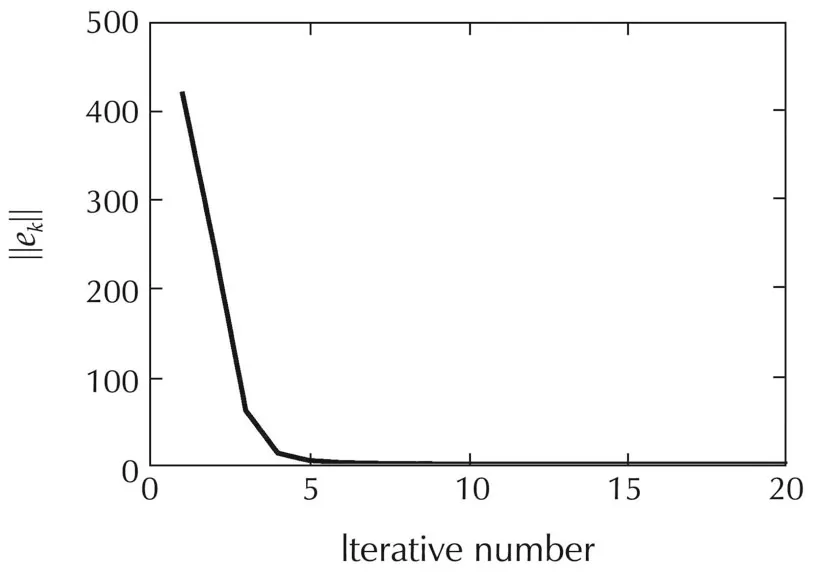
Fig.3 Tracking error of SR1(SR2)-ILC.

Fig.4 Tracking errors of SR1(SR2)-ILC and NOILC.

Fig.5 Tracking errors of SR1(SR2)-ILC and PA-ILC.

Example 3 In microelectronics manufacturing,in order to guarantee the rapid thermal processing to work at the designed set-point,the temperature of the mono-crystal reactor must be tuned to follow an operating trajectory[6].As the rapid thermal processing is usually scheduled as a repetitive batch process,the ILC scheme is adequately to be utilized so that transient temperature of the reactor to follow a desired trajectory.Suppose that the transfer function of the reactor is identified aswhere K is the process gain,τWdenotes the heating time constant of the crystal and τLthe heating time constant of the crystal light.Conventionally,the power ratio of the crystal light is tuned by a proportional-derivative-integral(PID)controller.Given that the transfer function of the PID controller iswhere KC,τIand τDare proportional,integral and derivative gains,respectively[6].By converting the dynamics of frequency domain into that of time domain and then discretizing the PID-controller-tuned closed-loop control system with the 0.05s sampling step,the discrete time system is described as follows:

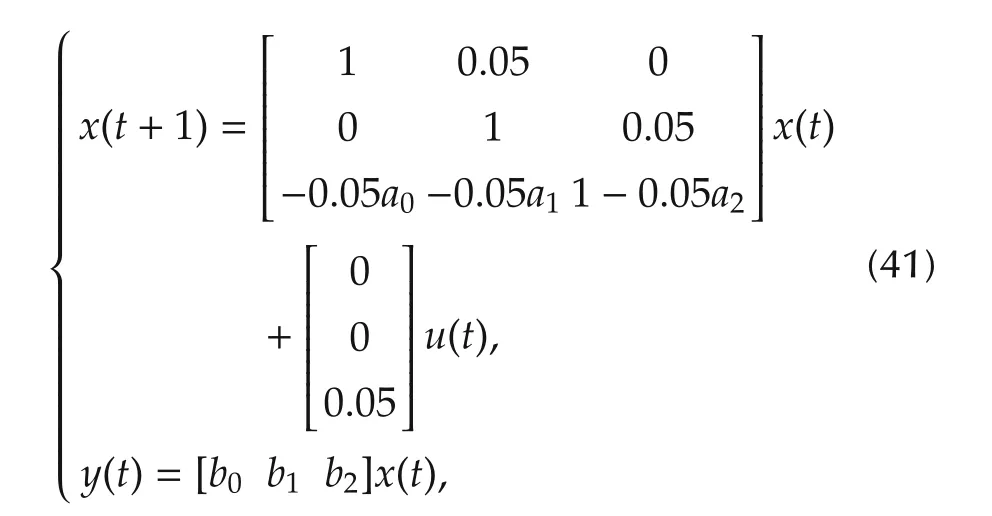
where

By setting a group of parameters as K=0.9,τW=5,τL=1,KC=1.51,τI=15 and τD=3.33.Set the initial state xk(0)=[0 0 0]Tand the initial u1(t)=0,where t∈[0,100].The desired trajectory is defined as yd(t)=1-exp(-0.4t).The comparative tracking error of the proposed quasi-Newton ILC scheme with that of the Gradient-type ILC and the NOILC is exhibited in Fig.6,whilst the outputs at the 12th iteration of the the pro-posed quasi-Newton ILC scheme,the Gradient-type ILC and the NOILC are displayed in Fig.7.

It is seen from Figs.6 and 7 that the proposed quasi-Newton SR1(SR2)-ILC owns better tracking performance.

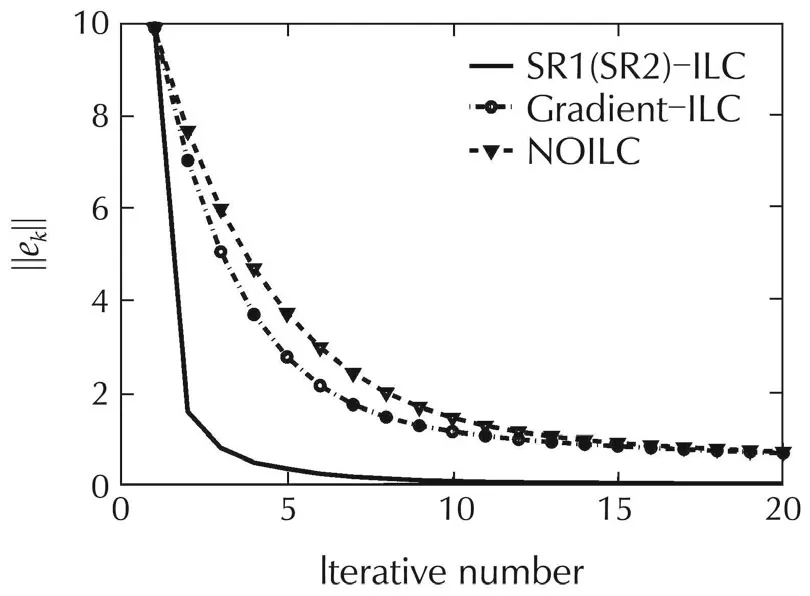
Fig.6 Comparative tracking errors.

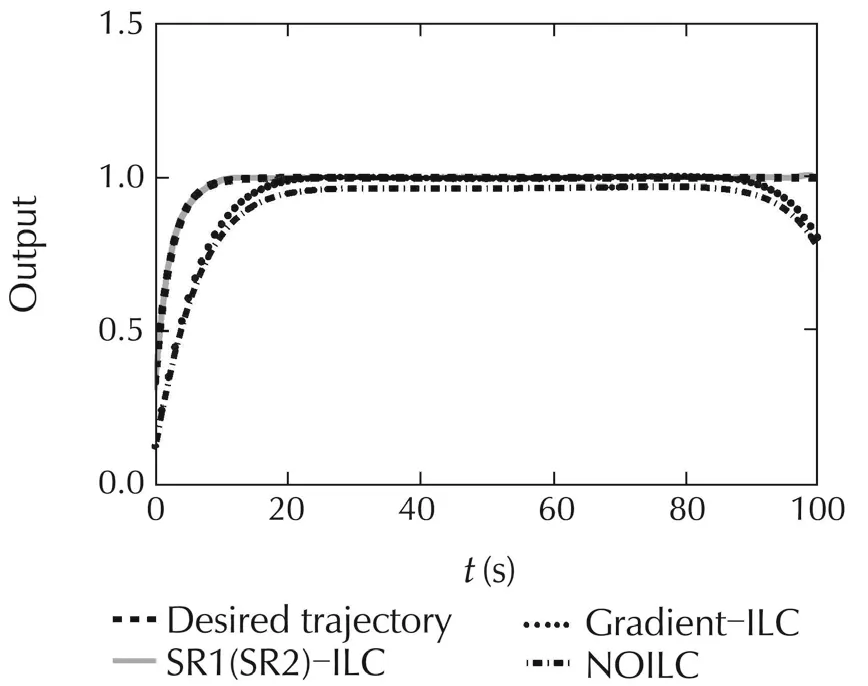
Fig.7 Comparative tracking performance at the 12th iteration.

5 Conclusions

In this paper,a quasi-Newton-type optimized ILC is proposed for a class of discrete linear time-invariant SISO systems.The idea is to use an approximation ma-trix to replace the inverse model of the plant.The conver-gence analysis indicates that the proposed ILC algorithm performs well with the tracking error vanishing within finite iterations.Numerical simulations testify that the proposed quasi-Newton-type optimized ILC scheme is effective though the system is ill-conditioned.However,the proposed scheme requires a precise knowledge of the system.In reality,the system is unavoidably perturbed by noise and sometimes the system is nonlinear.How to solve the perturbation and the nonlinearity is challenging in the future.

[1]S.Arimoto,S.Kawamura,F.Miyazaki.Bettering operation of robots by learning.Journal of Robotic Systems,1984,1(2):123-140.

[2]N.Amann,D.H.Owens,E.Rogers.Iterative learning control for discrete-time systems with exponential rate of convergence.IEE Proceedings-Control Theory and Applications,1996,143(2):217-224.

[3] J.Xu.Analysis of iterative learning control for a class of nonlinear discrete-time systems.Automatica,1997,33(10):1905-1907.

[4]J.H.Lee,K.S.Lee,W.C.Kim.Model-based iterative learning control with quadratic criterion for time-varying linear systems.Automatica,2000,36(5):641-657.

[5] D.Meng,Y.Jia,J.Du,et al.Feedback iterative learning control for time-delay systems based on 2D analysis approach.Journal of Control Theory and Applications,2010,8(4):457-463.

[6] X.Ruan,Z.Li.Convergence characteristics of PD-type iterative learning control in discrete frequency domain.Journal of Process Control,2014,24(12):86-94.

[7]X.Ruan,Z.Z.Bien,Q.Wang.Convergence characteristics of proportional-type iterative learning control in the sense of Lebesgue-p norm.IET Control Theory and Applications,2012,6(5):707-714.

[8] S.S.Saab.A discrete-time stochastic learning control algorithm.IEEE Transactions on Automatic and Control,2001,46(6):877-887.

[9]C.Yin,J.Xu,Z.Hou.A high-order internal model based iterative learning control scheme for nonlinear systems with time iteration-varying parameters.IEEE Transactions on Automatic Control,2010,55(11):2665-2670.

[10]A. Tayebi,M. B. Zaremba.Robust iterative learning control design is straightforward for uncertain LTI systems satisfying the robust performance condition.IEEE Transactions on Automatic Control,2003,48(1):101-106.

[11]T.Liu,X.Wang,J.Chen.Robust PID based indirect-type iterative learning control for batch processes with time-varying uncertainties.Journal of Process Control,2014,24(12):95-106.

[12]H.S.Ahn,K.L.Moore,Y.Chen.Stability analysis of discrete time iterative learning control systems with interval uncertainty.Automatica,2007,43(5):892-902.

[13]Y.Chen,C.Wen,Z.Gong,et al.An iterative learning controller with initial state learning.IEEE Transactions on Automatic Control,1999,44(2):371-376.

[14]J.H.Lee,K.S.Lee,W.C.Kim.Model-based iterative learning control with a quadratic criterion control with a quadratic criterion for time-varying linear systems.Automatica,2000,36(5):641-657.

[15]D.H.Owens,K.Feng.Parameter optimization in iterative learning control.International Journal of Control,2003,76(11):1059-1069.

[16]D.H.Owens,J.H¨at¨onen,S.Daley.Robust monotone gradient-based discrete-time iterative learning control,time and frequency domain conditions.International Journal of Robust Nonlinear Control,2009,19(6):634-661.

[17]T.J.Harte,J.H¨at¨onen,D.H.Owens.Discrete-time inverse model-based iterative learning control,stability,monotonicity and robustness.International Journal of Control,2006,78(8):577-586.

[18]D.H.Owens,B.Chu,M.Songjun.Parameter-optimal iterative learning control using polynomial representations of the inverse plant.International Journal of Control,2012,85(5):533-544.

[19]X.Yang,X.Ruan.Conjugate direction method of iterative learning control for linear discrete time-invariant systems.Dynamics of Continuous,Discrete and Impulsive Systems-Series B:Applicationsamp;Algorithms,2013,20(5):543-554.

[20]M.Norrl¨of.An adaptive iterative learning control algorithm with experiments on an industrial robot.IEEE Transactions on Robotics and Automation,2002,18(2):245-251.

[21]W.Li,P.Maisse,H.Enge.Self-learning control applied to vibration control of a rotating spindle by piezopusher bearings.Proceedings of the Institution of Mechanical Engineers-Part I:Journal of Systems and Control Engineering,2004,218(13):185-196.

[22]K.S.Lee,J.H.Lee.Convergence of constrained model-based predictive control for batch processes.IEEE Transactions on Automatic Control,2000,45(10):1928-1932.

[23]H.S.Ahn,Y.Chen,K.L.Moore.Iterative learning control:brief survey and categorization.IEEE Transactions on Systems,Man,and Cybernetics-Part C:Applications and Reviews,2007,37(6):1099-1121.

[24]P.Hennig,M.Kiefel.Quasi-Newton methods:a new direction.Proceedings of the 29th International Conference on Machine Learning,Edinburgh,Scotland,2012:http://icml.cc/2012/papers/25.pdf.

[25]L.Dumas, V.Herbert, F. Muyl. Comparison of global optimization methods for drag reduction in the auto motive industry.International Conference on Computational Science and Its Applications,Berlin:Springer,2005:948-957.

[26]Y.S.Ong,P.B.Nair,A.J.Keane.Evolutionary optimization of computationally expensive problems via surrogate modeling.AIAA Journal,2003,41(4):687-696.

[27]Y.Yuan,W.Sun.Theory and Methods of Optimization.Beijing:Science Press,1997.

[28]J.Nocedal,S.J.Wright.Numerical Optimization.New York:Springer,2006.

[29]Y. Fang, T.W. S. Chow. Iterative learning control of linear discrete-time multi variable systems. Automatica, 1998, 34(11): 1459 - 1462.

[30]A.Madady.PID type iterative learning control with optimal gains.International Journal of Control Automation and Systems,2008,6(2):194-203.

5 November 2014;revised 4 July 2015;accepted 6 July 2015

DOI10.1007/s11768-015-4161-z

†Corresponding author.

E-mail:wruanxe@mail.xjtu.edu.cn.Tel.:+86-13279321898.

This work was supported by the National Natural Science Foundation of China(Nos.F010114-60974140,61273135).

©2015 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg

Yan GENG received the B.Sc.degree in Mathematics from Changzhi University,China in 2009.She received the M.Sc.degree in Mathematics from Hebei University,China,in 2012.Currently,she is a Ph.D.candidate of Xi’anJiaotong University,China.Her research interests are iterative learning control and optimization.E-mail:gengyan104@stu.xjtu.edu.cn.

Xiaoe RUAN received the B.Sc.and M.Sc.degrees in Pure Mathematics Education from Shaanxi Normal University,China,in 1988 and 1995,respectively.She received the Ph.D.degree in Control Science and Engineering from Xi’an Jiaotong University,China,in 2002.From March 2003 to August 2004,she worked as a postdoctoral fellow at the Department of Electrical Engineering,Korea Advance Institute of Science and Technology,Korea.From September2009to August 2010,she worked as a visiting scholar at Ulsan National Institute of Science and Technology,Korea.Since 1995,she joined in Xi’an Jiaotong University.Currently,she is a full professor in School of Mathematics and Statistics.She has published more than 40 academic papers.Her research interests include iterative learning control and optimized control for large-scale systems.E-mail:wruanxe@xjtu.edu.cn.